Похожие презентации:
Трапеция и средняя линия трапеции
1.
МАОУ Ильинская СОШУчитель математики и информатики:
С.А.Абрамкина
2.
Давайте вспомним определениеи свойства параллелограмма
Тест
01.03.2019
С.А. Абрамкина
3.
ВF
№56.
С
Е
G
Дано: АВСD – четырехугольник
AE=ED, BF=FC, CG=GD, AH=HD,
EFGH – параллелограмм
BD = 12м, AC = 10м.
Найти: EF, FG, GH, EH
А
H
D
Решение:
EF – средняя линия ∆АВС;
GH – средняя линия ∆АСD;
ЕH – средняя линия ∆АВD;
FG – средняя линия ∆ВСD;
Отсюда
1
EF=GH= AC=5м
2
1
EH=FG= BD=6м.
2
Ответ: 5м, 6м.
01.03.2019
С.А. Абрамкина
4.
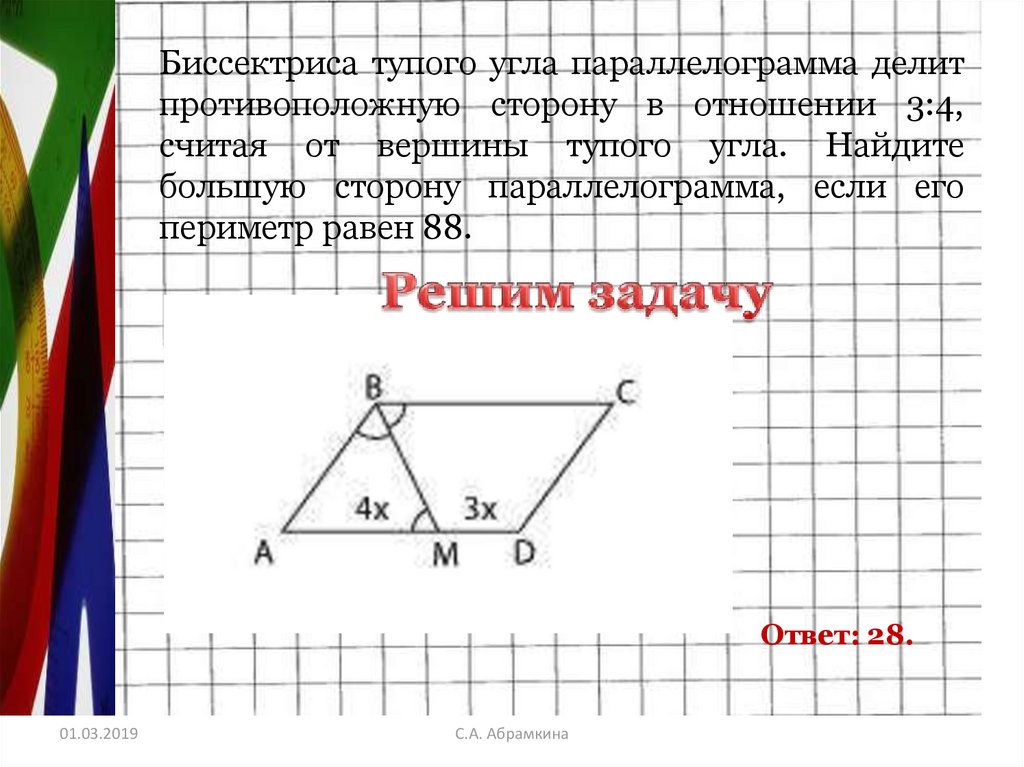
Биссектриса тупого угла параллелограмма делитпротивоположную сторону в отношении 3:4,
считая от вершины тупого угла. Найдите
большую сторону параллелограмма, если его
периметр равен 88.
Ответ: 28.
01.03.2019
С.А. Абрамкина
5.
Геометрическая фигура была названатак по внешнему сходству с маленьким
столом.
01.03.2019
С.А. Абрамкина
6.
01.03.2019С.А. Абрамкина
7.
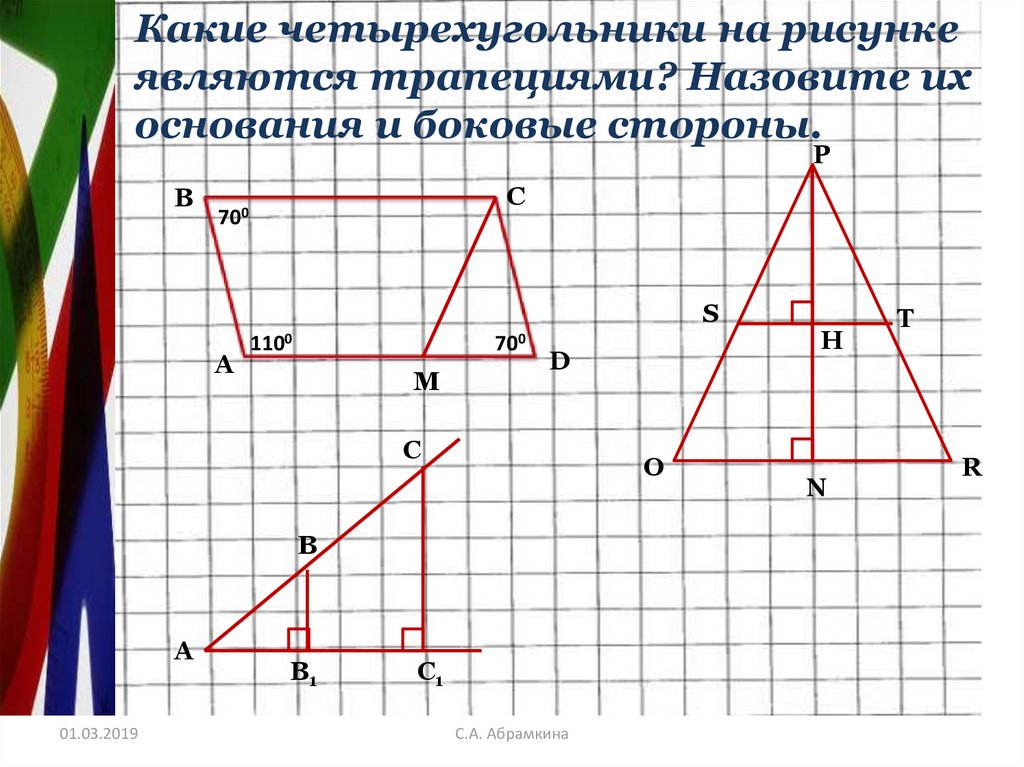
Какие четырехугольники на рисункеявляются трапециями? Назовите их
основания и боковые стороны.
P
В
С
700
S
А
1100
700
М
D
С
О
В
А
01.03.2019
B1
С1
С.А. Абрамкина
H
N
T
R
8.
01.03.2019С.А. Абрамкина
9.
01.03.2019С.А. Абрамкина
10.
2. В трапеции АВСD известны основания1. Основание трапеции равны 7 см и
АD=10см, ВС=6см и боковые стороны
9АВ=4см,
см. Чему
равнаЧему
средняя
СD=5см.
равнылиния
стороны
трапеции?
четырехугольника AEFD, если EF –
средняя линия трапеции АВСD?
В
Ответ:
8 см
6
С
F
E
А
10
D
Ответ: 2см, 8 см, 2,5см, 10см
01.03.2019
С.А. Абрамкина
11.
1. Докажите, что у равнобокой трапеции углы при основанииравны
2. В равнобокой трапеции АВСDк большему основанию АD
проведена высота ВН. Докажите, что точка Н разбивает
основание на отрезки, один из которых равен полусумме
оснований (т.е. средней линии трапеции), а другой –
полуразности оснований трапеции.
3. Докажите, что диагонали равнобокой трапеции равны.
01.03.2019
С.А. Абрамкина
12.
ВС
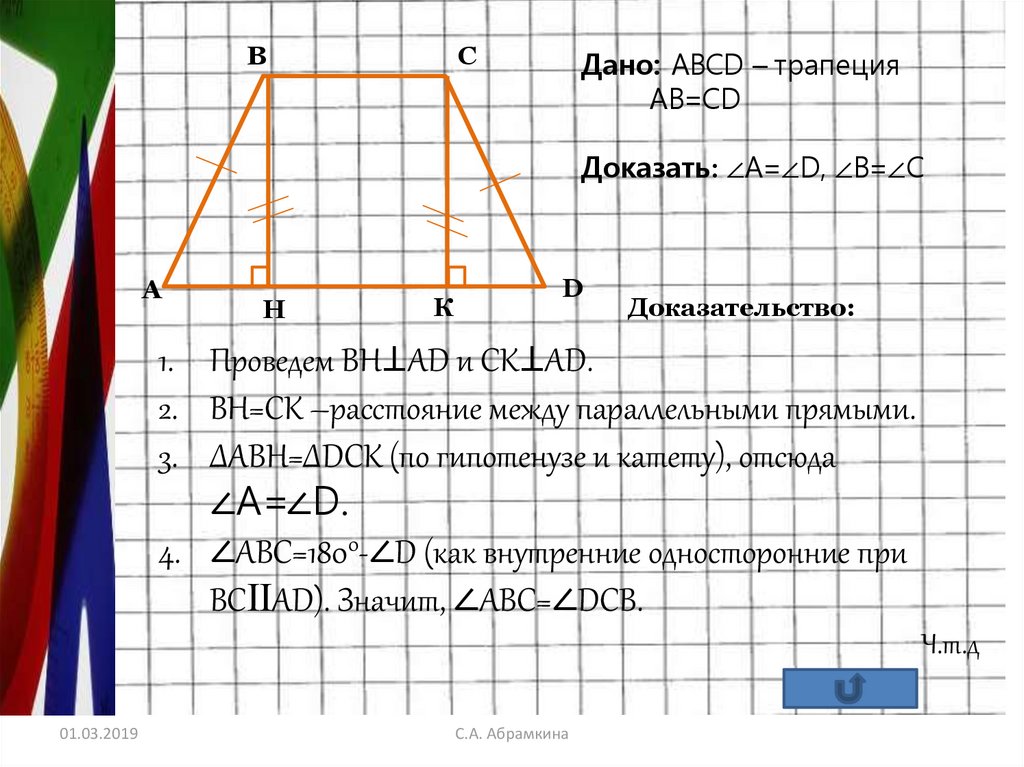
Дано: АВСD – трапеция
AВ=СD
Доказать: ∠А=∠D, ∠В=∠С
А
Н
К
D
Доказательство:
1. Проведем ВН⊥АD и СК⊥АD.
2. ВН=СК –расстояние между параллельными прямыми.
3. ∆АВН=∆DСК (по гипотенузе и катету), отсюда
∠А=∠D.
4. ∠АВС=1800-∠D (как внутренние односторонние при
ВСⅡАD). Значит, ∠АВС=∠DСВ.
Ч.т.д
01.03.2019
С.А. Абрамкина
13.
ВС
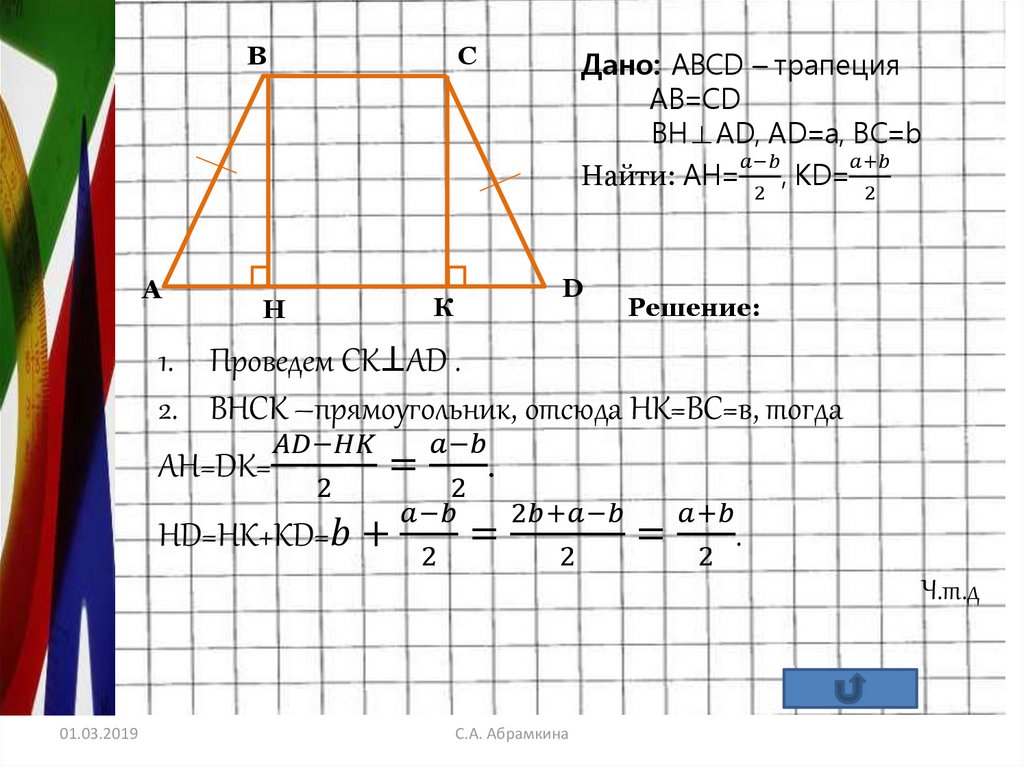
Дано: АВСD – трапеция
AВ=СD
ВН⊥АD, AD=a, ВC=b











 Математика
Математика








