Наш мир – это удивительный мир симметрии

1. Наш мир – это удивительный мир симметрии.

Симметрия является одной из
наиболее общих закономерностей
живой природы, неживой природы и
общества.

2.

Слово
«симметрия»
греческого
происхождения («сим» - с, «метрон» мера)
и
буквально
означает
«соразмерность».
Симметрия является той идеей, с
помощью которой человек веками
пытается объяснить и создать
порядок, красоту и совершенство.
Герман Вейль.

3. Букет цветов

4. Морская звезда

5. Взрыв новой звезды.

6. Георгин

7. Кувшинка

8.

А
а
А1
Две точки А и А1 называются симметричными
относительно прямой а, если эта прямая проходит
через середину отрезка АА1 и перпендикулярна к
нему.
Прямая а называется осью симметрии.

9.

Фигура
называется
симметричной
относительно прямой а, если для каждой точки
фигуры симметричная ей точка относительно
прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
а

10. Задание №1

• Какие из букв русского алфавита имеют
горизонтальную ось симметрии:
А Б В Г Д ЕЖ З И К Л
МНОПРСТУЧШ
ЩЪЫЬЭЮЯ?

11.

ВЕЖЗКНОС
ФХЭЮ

12. Какие из букв русского алфавита имеют вертикальную ось симметрии:

•А Б В Г Д ЕЖ З И К Л
МНОПРСТУЧШ
ЩЪЫЬЭЮЯ?

13.

АДЖЛМНО
ПТФХШ

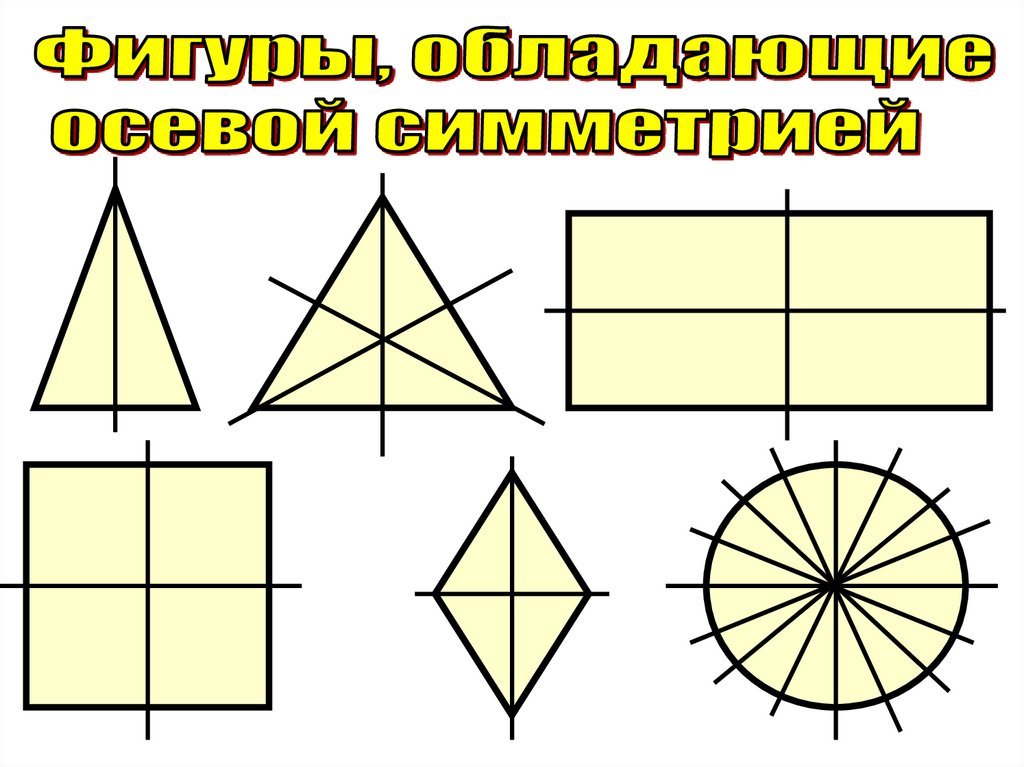
14. Задание №3. Какие из данных геометрических фигур имеют ось симметрии?

• Произвольный треугольник,
равнобедренный треугольник,
равносторонний треугольник,
параллелограмм, ромб,
прямоугольник, круг, квадрат,
произвольная трапеция.

15.

16.

17.

Две точки
А и А1 называются симметричными
относительно точки О, если О – середина отрезка.
Точка О – называется центром симметрии
А1
О
А

18.

Фигура называется симметричной относительно точки О,
если для каждой точки фигуры симметричная ей точка
относительно точки О также принадлежит этой фигуре.
Точка О называется центром симметрии фигуры.

19. Задание №4. Используя осевую симметрию, достроить «дворец».

20.

21. Пример поворотной симметрии – спиральная галактика. (Галактика – скопление звезд)

22. И обычная шаровая галактика.