Похожие презентации:
Решение задач на применение признаков равенства треугольников
1. Решение задач на применение признаков равенства треугольников.
2.
Цели:• Закрепить навыки использования
признаков равенства треугольников при
решении задач. Систематизировать,
расширить и углубить знания учащихся о
треугольнике, закрепить навыки и
умения при решении задач, используя
определения и теоремы по данной теме.
3.
Ход урока
1.Организационный момент
2.Повторение
3.Изучение нового материала
4.Закрепление из материала
5.Домашнее задание
4.
• Если вы хотите научитьсяплавать, то смело входите в воду,
• а если хотите научиться решать
задачи, то решайте их.
• (Д.Пойа)
5.
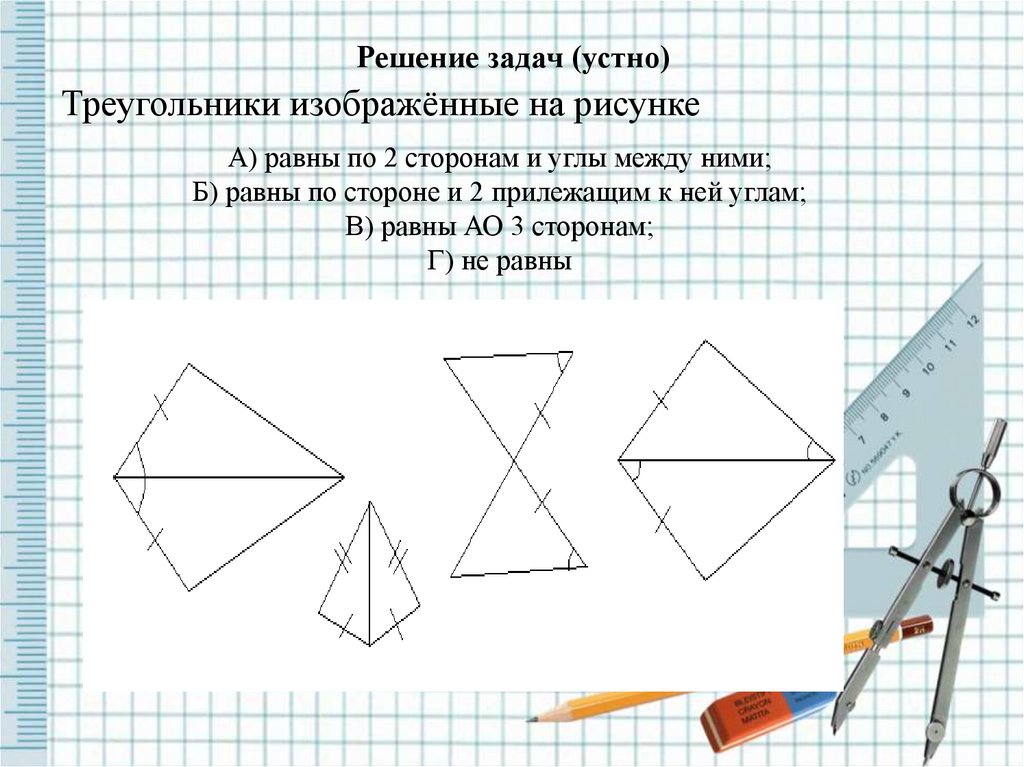
Решение задач (устно)Треугольники изображённые на рисунке
А) равны по 2 сторонам и углы между ними;
Б) равны по стороне и 2 прилежащим к ней углам;
В) равны АО 3 сторонам;
Г) не равны
6.
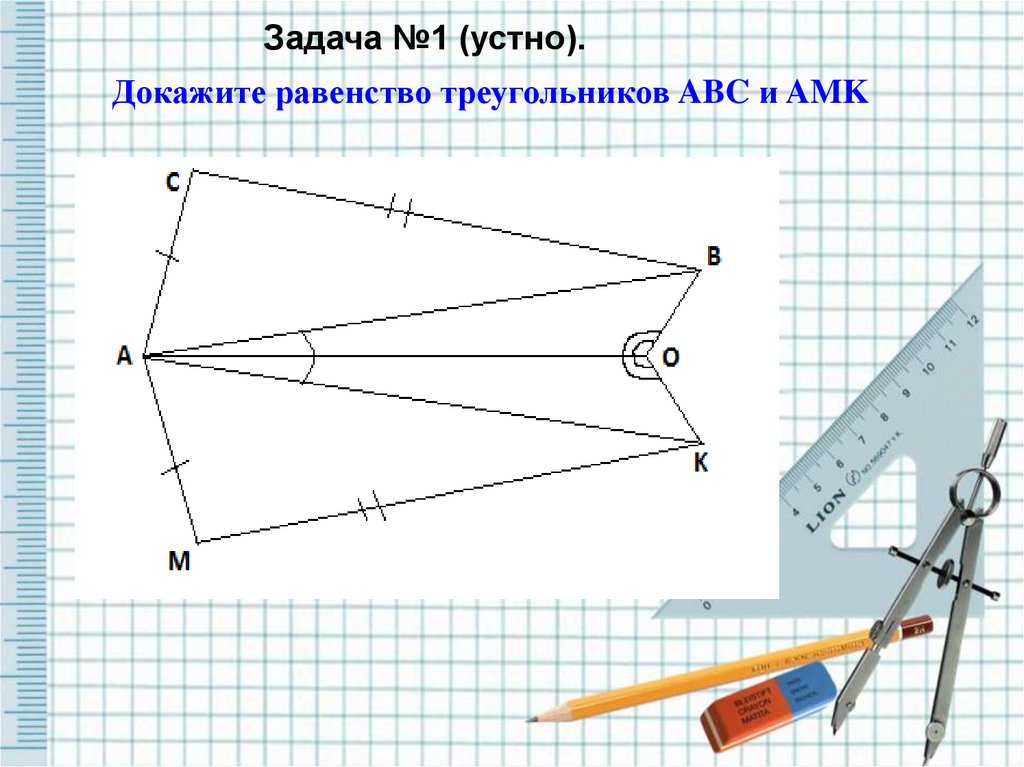
Задача №1 (устно).Докажите равенство треугольников ABC и AMK
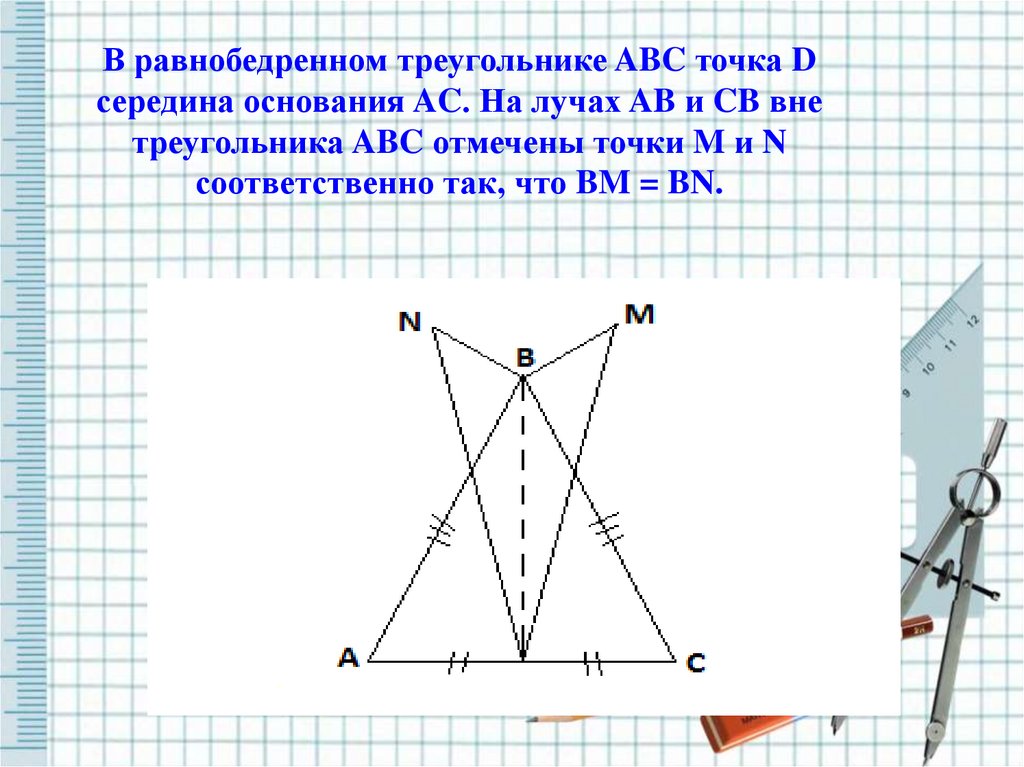
7. В равнобедренном треугольнике ABC точка D середина основания AC. На лучах AB и CB вне треугольника ABC отмечены точки M и N
соответственно так, что BM = BN.8.
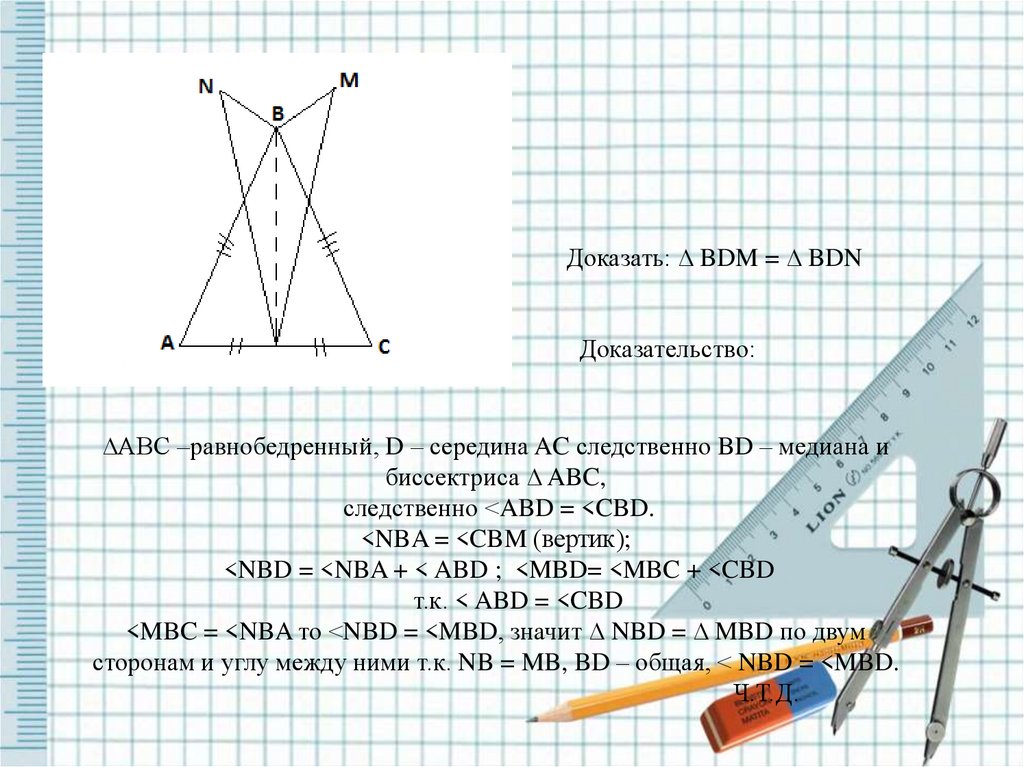
Доказать: ∆ BDM = ∆ BDNДоказательство:
∆ABC –равнобедренный, D – середина AC следственно BD – медиана и
биссектриса ∆ ABC,
следственно <ABD = <CBD.
<NBA = <CBM (вертик);
<NBD = <NBA + < ABD ; <MBD= <MBC + <CBD
т.к. < ABD = <CBD
<MBC = <NBA то <NBD = <MBD, значит ∆ NBD = ∆ MBD по двум
сторонам и углу между ними т.к. NB = MB, BD – общая, < NBD = <MBD.
Ч.Т.Д.
9.
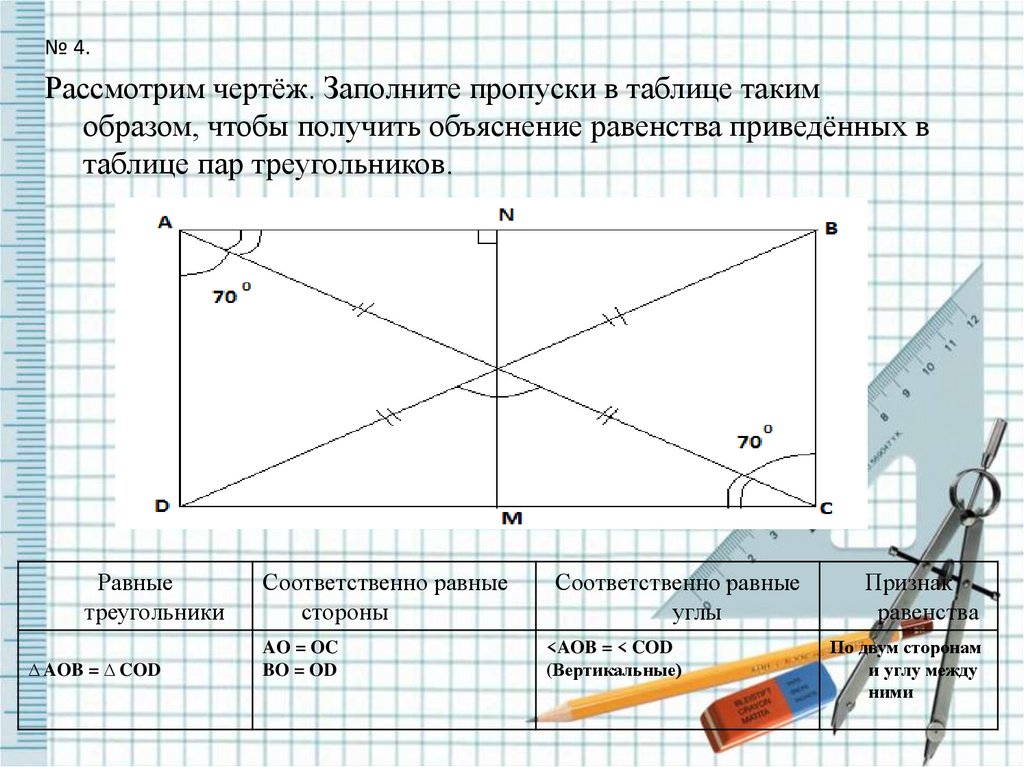
№ 4.Рассмотрим чертёж. Заполните пропуски в таблице таким
образом, чтобы получить объяснение равенства приведённых в
таблице пар треугольников.
Равные
треугольники
∆ AOB = ∆ COD
Соответственно равные
стороны
AO = OC
BO = OD
Соответственно равные
углы
<AOB = < COD
(Вертикальные)
Признак
равенства
По двум сторонам
и углу между
ними
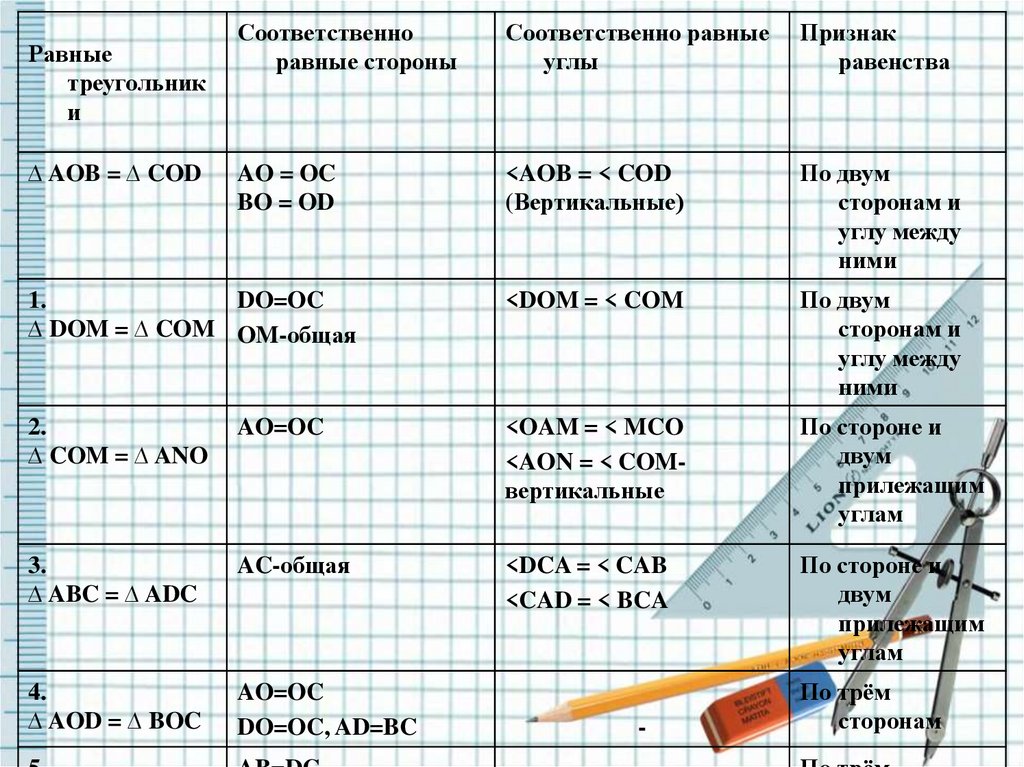
10.
Соответственноравные стороны
Соответственно равные
углы
Признак
равенства
AO = OC
BO = OD
<AOB = < COD
(Вертикальные)
По двум
сторонам и
углу между
ними
1.
DO=OC
∆ DOM = ∆ COM OM-общая
<DOM = < COM
По двум
сторонам и
углу между
ними
2.
∆ COM = ∆ ANO
AO=OC
<OAM = < MCO
<AON = < COMвертикальные
По стороне и
двум
прилежащим
углам
3.
∆ ABC = ∆ ADC
AC-общая
<DCA = < CAB
<CAD = < BCA
По стороне и
двум
прилежащим
углам
4.
∆ AOD = ∆ BOC
AO=OC
DO=OC, AD=BC
Равные
треугольник
и
∆ AOB = ∆ COD
-
По трём
сторонам
11. Домашнее задание:
• написать свой рассказ «Что такоетреугольник».
• П.19,20 №136, 140





 Математика
Математика








