Теоремы Чевы и Менелая

1. Презентация к уроку

Геометрия 10 класс
Теоремы Чевы и Менелая

2. Теоремы Чевы и Менелая

«Обладая литературой более обширной, чем
алгебра и арифметика вместе взятые, и по
крайней мере столь же обширной, как анализ,
геометрия в большей степени чем любой
другой раздел математики, является
богатейшей сокровищницей интереснейших,
но полузабытых вещей, которыми спешащее
поколение не имеет времени насладиться».
Е. Т. Белл.

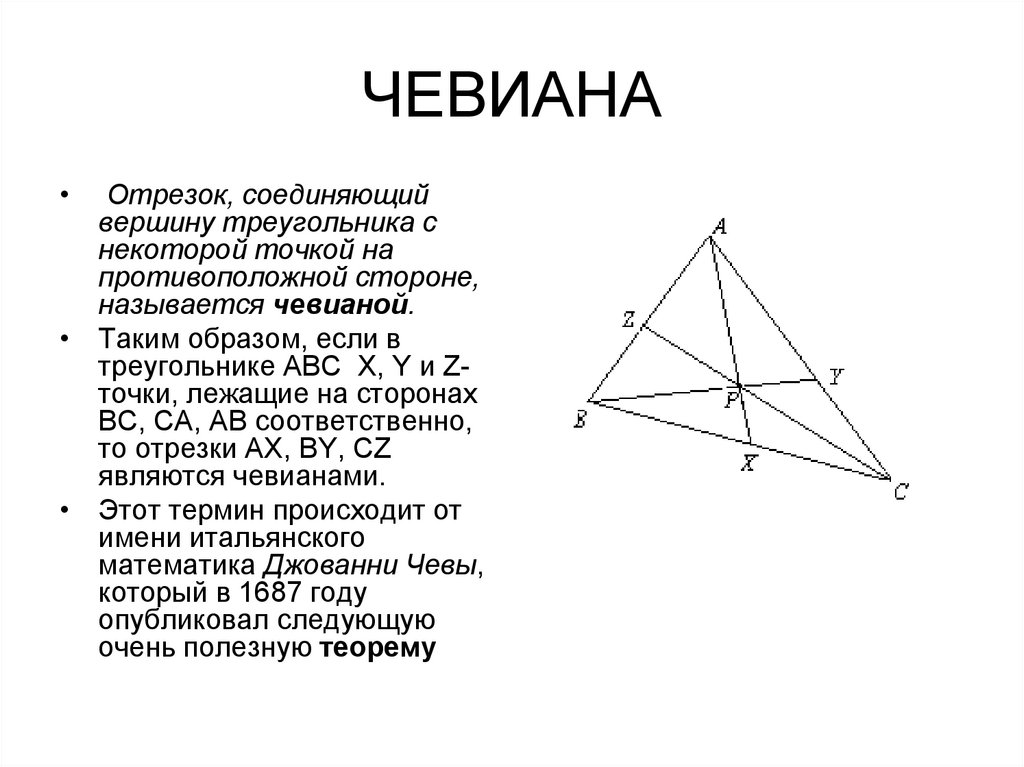
3. ЧЕВИАНА

Отрезок, соединяющий
вершину треугольника с
некоторой точкой на
противоположной стороне,
называется чевианой.
• Таким образом, если в
треугольнике АВС X, Y и Zточки, лежащие на сторонах
ВС, СА, АВ соответственно,
то отрезки АX, ВY, СZ
являются чевианами.
• Этот термин происходит от
имени итальянского
математика Джованни Чевы,
который в 1687 году
опубликовал следующую
очень полезную теорему

4.

Теорема названа в честь
итальянского математика
Джованни Чевы, который
доказал её в 1678 году.

5.

День рождения: 07.12.1647 года
Дата смерти: 15.06.1734 года
Гражданство: Италия
Джованни Чева родился в 1647 году в
Италии. Он окончил иезуитский
колледж в Милане, после чего стал
студентом Университета в Пизе, где
позже и стал работать профессором
математики.
С 1686 года Чева работал в
Университете в Мантуе, оставаясь на
этом посту до самого конца своей
жизни.
Университет Пизы .Университетом учебное заведение было признано в
1343 году декретом Папы Климента VI.

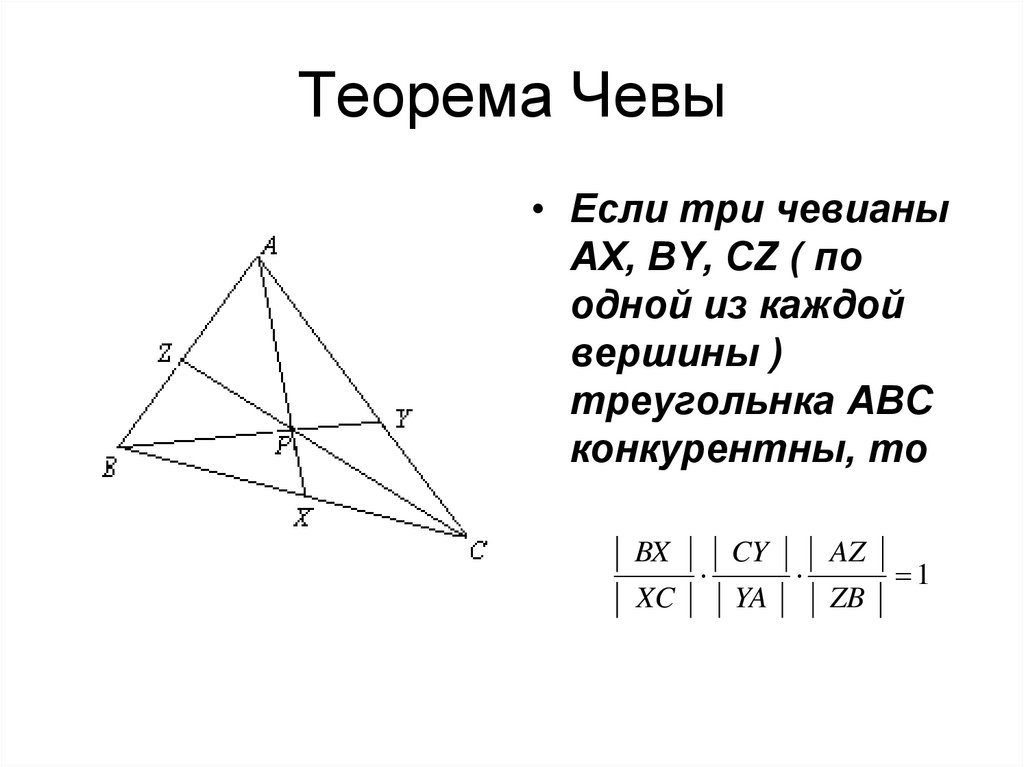
6. Теорема Чевы

• Если три чевианы
АX, ВY, СZ ( по
одной из каждой
вершины )
треугольнка АВС
конкурентны, то
BX
XC
CY
YA
AZ
ZB
1

7.

Когда мы говорим,
что три прямые (
или отрезка )
конкурентны, то
мы имеем в виду,
что все они
проходят через одну
точку, которую
обозначим через Р.

8. ДОКАЗАТЕЛЬСТВО

• Для доказательства теоремы Чевы
вспомним, что площади треугольников с
равными высотами пропорциональны
основаниям треугольников.
• Ссылаясь на рисунок, мы имеем
BX
XC
BX
XC
AZ
ZB
S ABX S BPX S ABX S BPX S ABP
S AXC S XPC S AXC S PXC SCPA
S ABX S BPX S ABX S BPX S ABP
S AXC S XPC S AXC S PXC S CPA
S ACZ S APZ S ACZ S APZ S ACP
S BCZ
S ZPB S BCZ S ZPB S BCP

9.

• Теперь, если мы перемножим их, то
получим
.
BX
CY
AZ
S ABP S CPB S ACP
х
х
1
XC YA ZB S CPA S ABP S BCP

10.

Рассмотрим доказательство некоторых
следствий теоремы Чевы.

11.

Задача 1: Доказать, что биссектрисы углов
треугольника пересекаются в одной точке.
Доказательство:
Пусть АА1, ВВ1, СС1 – биссектрисы
треугольника АВС.
Так как биссектриса угла треугольника делит
противолежащую сторону на отрезки,
длины которых пропорциональны
противолежащим сторонам, то
Перемножив полученные равенства,
получим:
Следовательно, по теореме Чевы,
биссектрисы пересекаются в одной точке.

12.

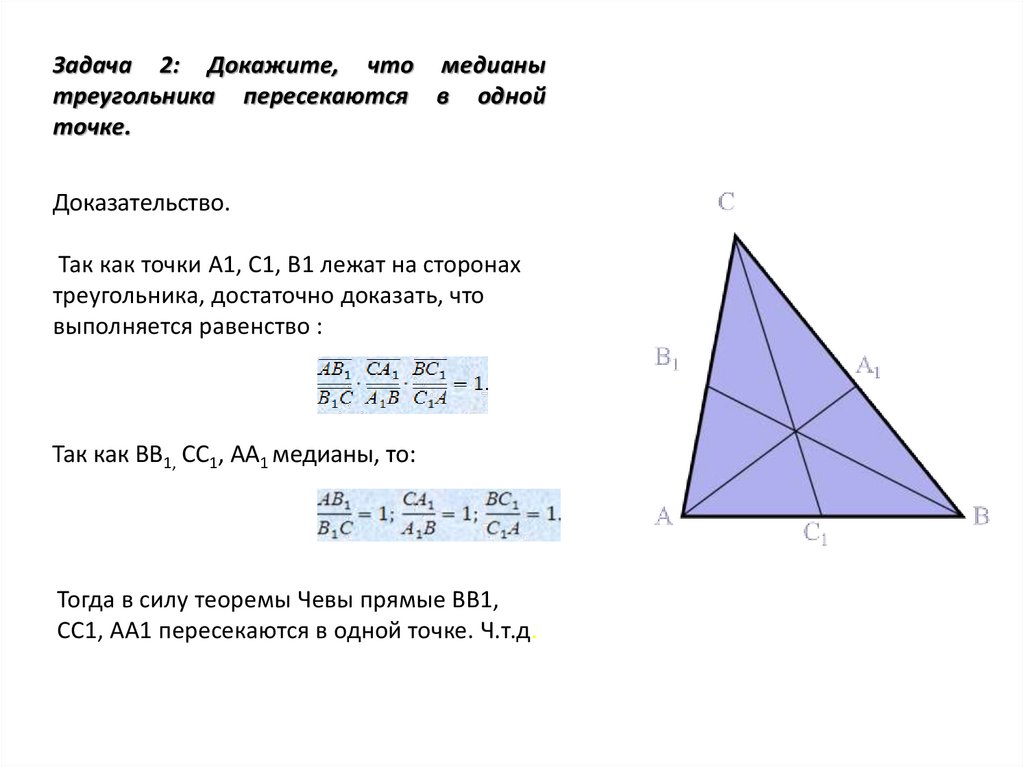
Задача 2: Докажите, что медианы
треугольника пересекаются в одной
точке.
Доказательство.
Так как точки А1, С1, В1 лежат на сторонах
треугольника, достаточно доказать, что
выполняется равенство :
Так как ВВ1, СС1, АА1 медианы, то:
Тогда в силу теоремы Чевы прямые ВВ1,
СС1, АА1 пересекаются в одной точке. Ч.т.д.

13. Теорема Менелая:

• Пусть точка А1 лежит на стороне ВС
треугольника АВС, точка С1 – на
стороне АВ, точка В1 – на продолжении
стороны АС за точку С. Точки А1,В1 иС1
лежат на одной прямой тогда и только
тогда, когда выполняется равенство
AC 1 BA1 CB1
1.
C 1B A1 C B1 A

14.

В
BA1 CB1 AC 1
1
A1 C B1 A C 1B
С1
А1
А
С
В1
CA1 BC 1 AB1
1.
A1 B C 1 A B 1 C
Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла
до нас в арабском переводе книги «Сферика» Менелая Александрийского.
Равенство Менелая можно записывать, начиная с любой вершины треугольника,
в любом направлении ( по часовой стрелке, против часовой стрелки ).

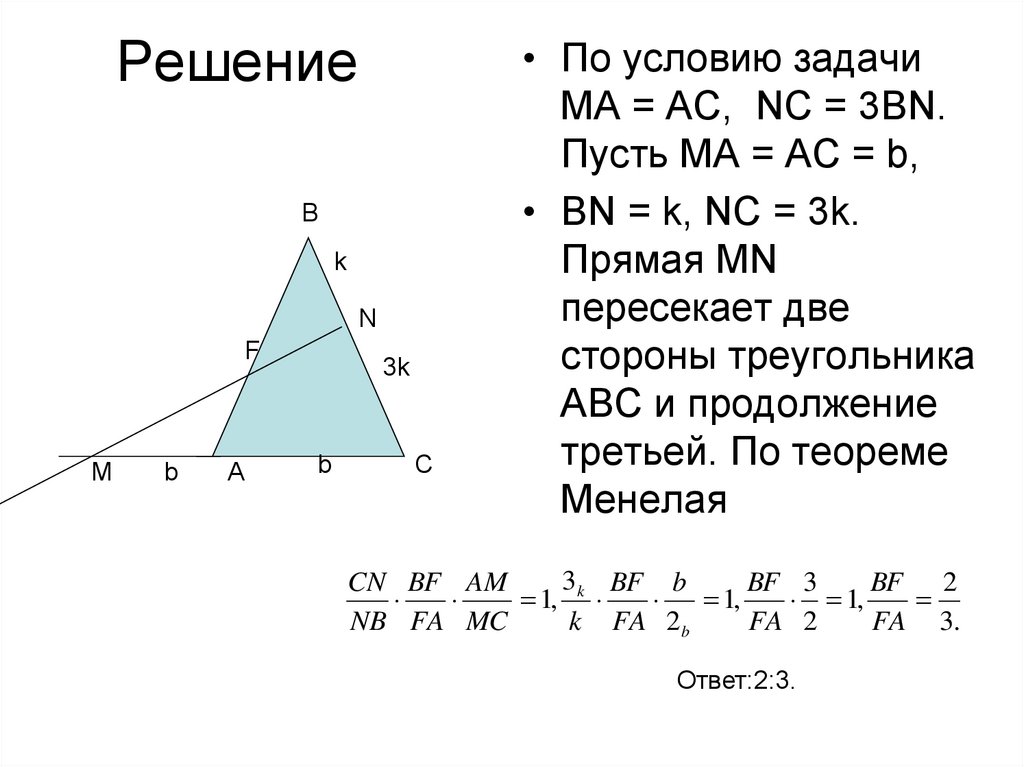
15. Задача 1. В треугольнике АВС на стороне ВС взята точка N так, что NC = 3BN; на продолжении стороны АС за точку А взята точка М

так, что МА=АС. Прямая
MN пересекает сторону АВ в точке F.
Найдите: отношение BF
FA

16. Решение

В
k
N
F
M
b
А
3k
b
C
• По условию задачи
МА = АС, NC = 3BN.
Пусть МА = АС = b,
• BN = k, NC = 3k.
Прямая MN
пересекает две
стороны треугольника
АВС и продолжение
третьей. По теореме
Менелая
3 BF b
CN BF AM
BF 3
BF 2
1, k
1,
1,
NB FA MC
k FA 2 b
FA 2
FA 3.
Ответ:2:3.