Парная регрессия и корреляция

1. Практикум по количественным методам

Занятие 1
Бурцева Юлия Валентиновна
[email protected]

2. Литература

3. Литература

4. Литература

Szd_Analyzdann_bBi_17.pdf

5. Регрессионный анализ

В зависимости от количества факторов,
включенных в регрессию, принято различать
регрессию простую и множественную.
Простая регрессия представляет собой регрессию между
двумя переменными (y и x), т.е. рассматривается
модель вида: y=f(x)
Множественная регрессия соответственно представляет
сбой регрессию результирующего признака с двумя и
большим числом факторов, т.е. рассматривается
модель y=f(x1,x2,x3,…)

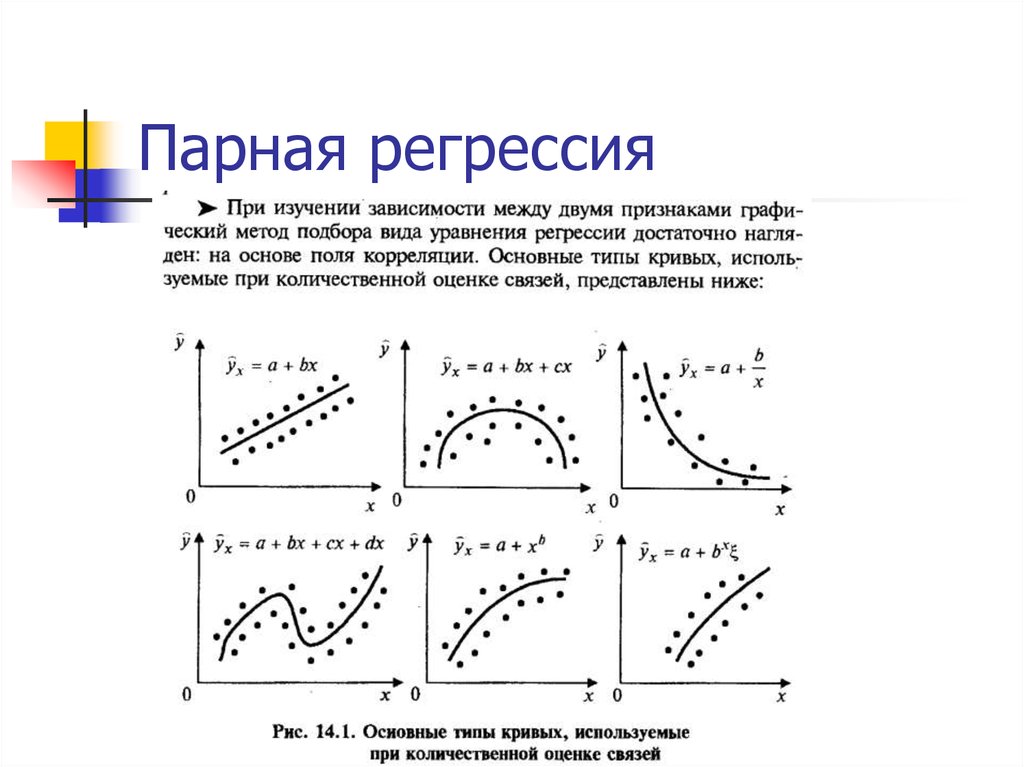
6. Парная регрессия

7. Парная регрессия

8. Парная регрессия

9. Парная регрессия

10. Парная регрессия

11. Парная регрессия

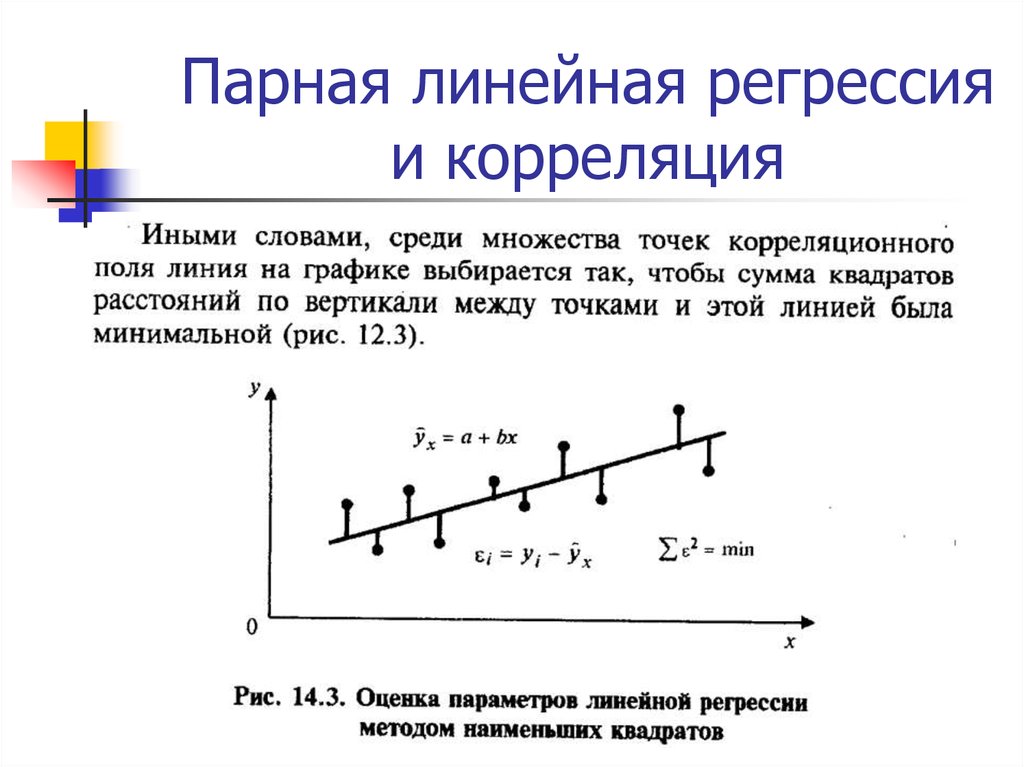
12. Парная линейная регрессия и корреляция

13. Парная линейная регрессия и корреляция

14. Парная линейная регрессия и корреляция

15. Парная линейная регрессия и корреляция

16. Парная линейная регрессия и корреляция

17. Парная линейная регрессия и корреляция

18. Парная линейная регрессия и корреляция

19. Парная линейная регрессия и корреляция

20. Парная линейная регрессия и корреляция

№
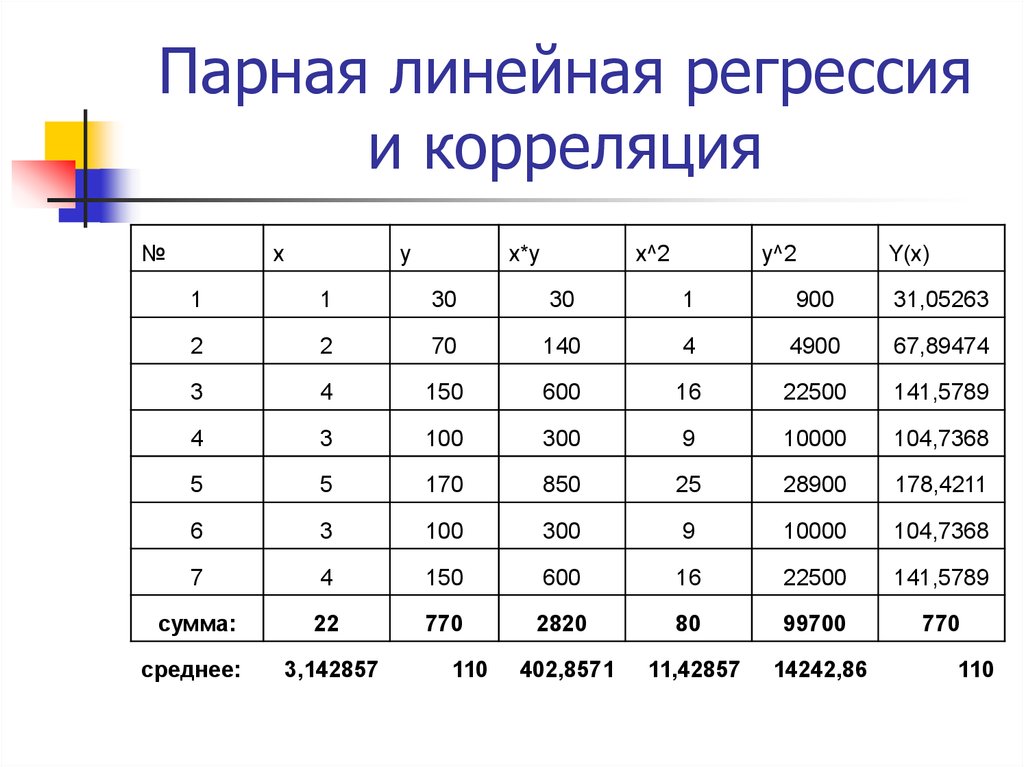
x
y
x*y
x^2
y^2
Y(x)
1
1
30
30
1
900
31,05263
2
2
70
140
4
4900
67,89474
3
4
150
600
16
22500
141,5789
4
3
100
300
9
10000
104,7368
5
5
170
850
25
28900
178,4211
6
3
100
300
9
10000
104,7368
7
4
150
600
16
22500
141,5789
сумма:
22
770
2820
80
99700
770
среднее:
3,142857
402,8571
11,42857
14242,86
110
110

21. Парная линейная регрессия и корреляция

x y
a
b
a bx y
na b x y
n
n
2
2
2
a
x
b
x
yx
x
x
yx
ax bx yx
a b
n
n
n
y x yx
b
b 36,84211
2
x x x
a 5.78947
a y b x
Определив коэффициенты получим уравнение :
y ( x) 5, 79 36,84 x

22. Парная линейная регрессия и корреляция

23. Парная линейная регрессия и корреляция

24. Парная линейная регрессия и корреляция

25. Парная линейная регрессия и корреляция

26. Парная линейная регрессия и корреляция

27. Оценка существенности параметров линейной регрессии и корреляции

28. Оценка существенности параметров линейной регрессии и корреляции

29. Оценка существенности параметров линейной регрессии и корреляции

30. Оценка существенности параметров линейной регрессии и корреляции

31. Оценка существенности параметров линейной регрессии и корреляции

32. Оценка существенности параметров линейной регрессии и корреляции

33. Оценка существенности параметров линейной регрессии и корреляции

34. Оценка существенности параметров линейной регрессии и корреляции