Похожие презентации:
Соотношение между сторонами и углами треугольника
1. Соотношение между сторонами и углами треугольника
Презентацию подготовилаУчитель математики
Серебрянская Л. А.
2.
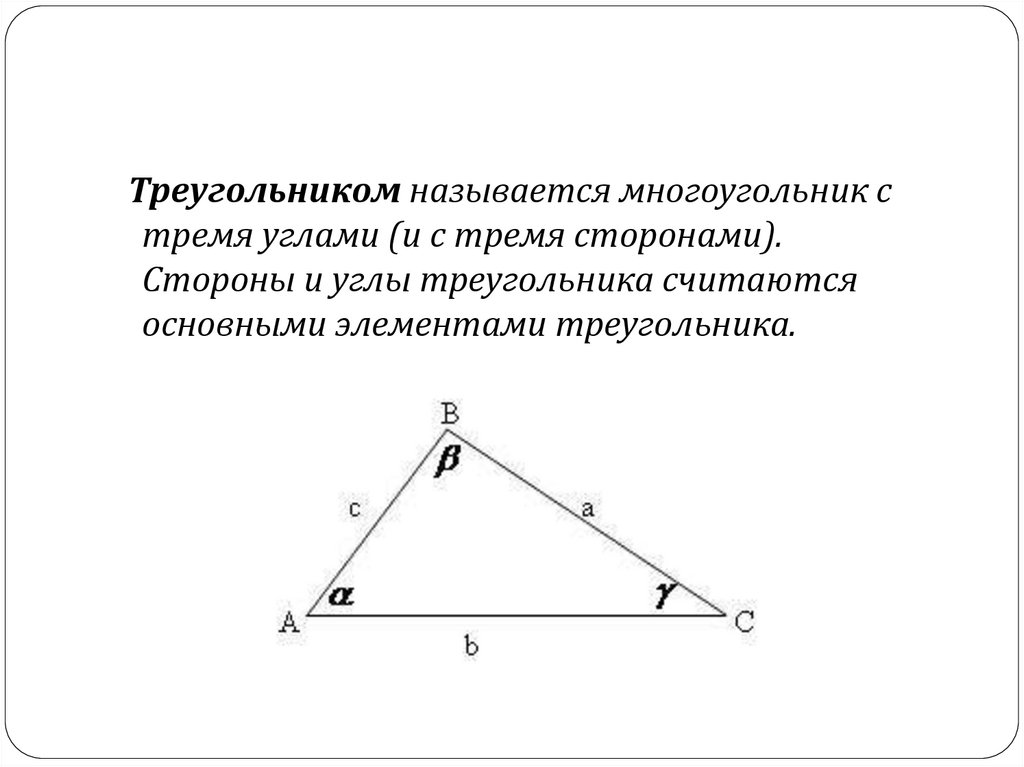
Треугольником называется многоугольник стремя углами (и с тремя сторонами).
Стороны и углы треугольника считаются
основными элементами треугольника.
3. Теорема
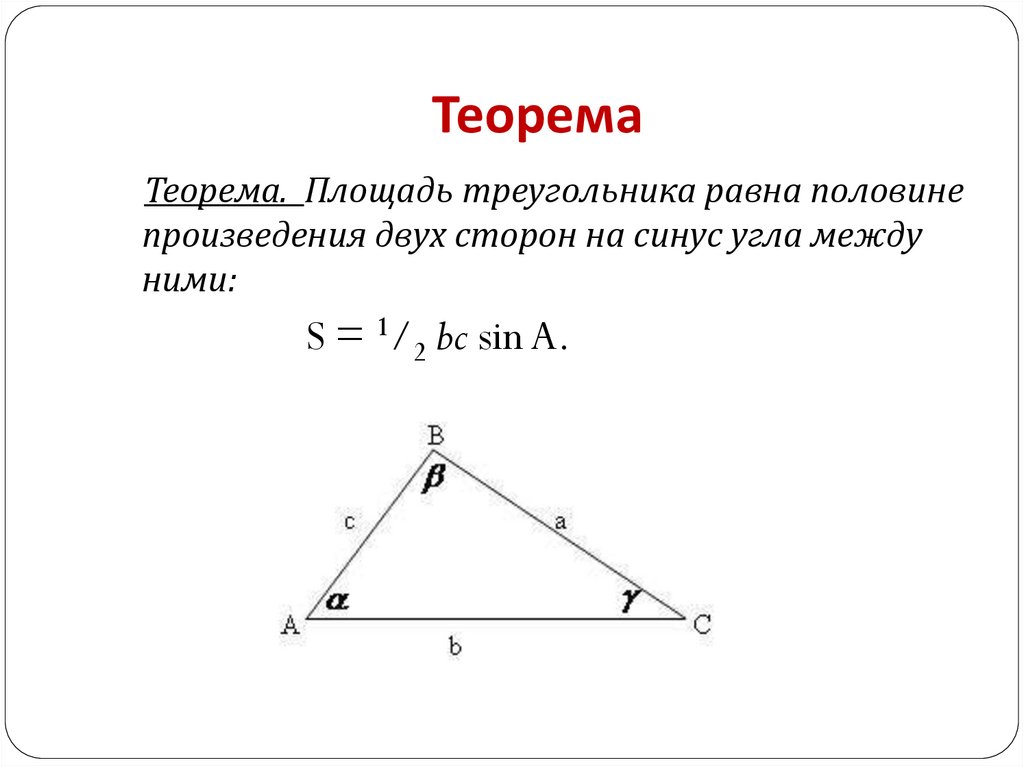
Теорема. Площадь треугольника равна половинепроизведения двух сторон на синус угла между
ними:
S = 1/2 bc sin A.
4. Теорема синусов
Для произвольного треугольникагде a, b, c — стороны треугольника,
α, β, γ — соответственно противолежащие им углы, а
R — радиус описанной около треугольника
окружности.
5. Теорема косинусов
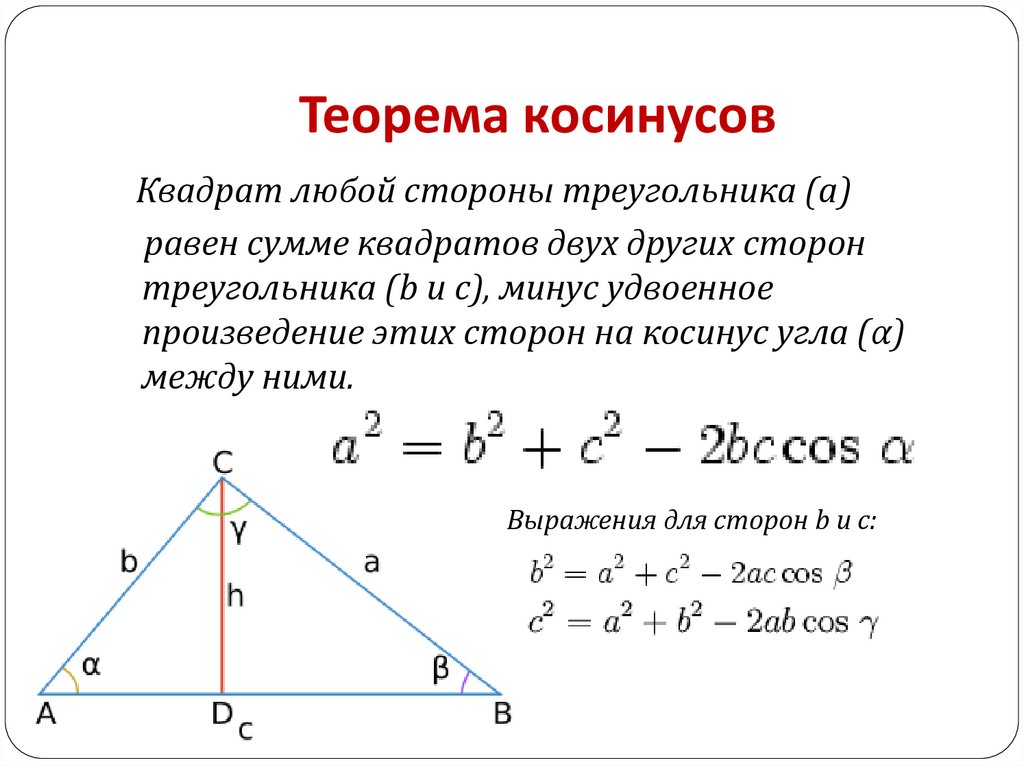
Квадрат любой стороны треугольника (a)равен сумме квадратов двух других сторон
треугольника (b и c), минус удвоенное
произведение этих сторон на косинус угла (α)
между ними.
Выражения для сторон b и c:
6. РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
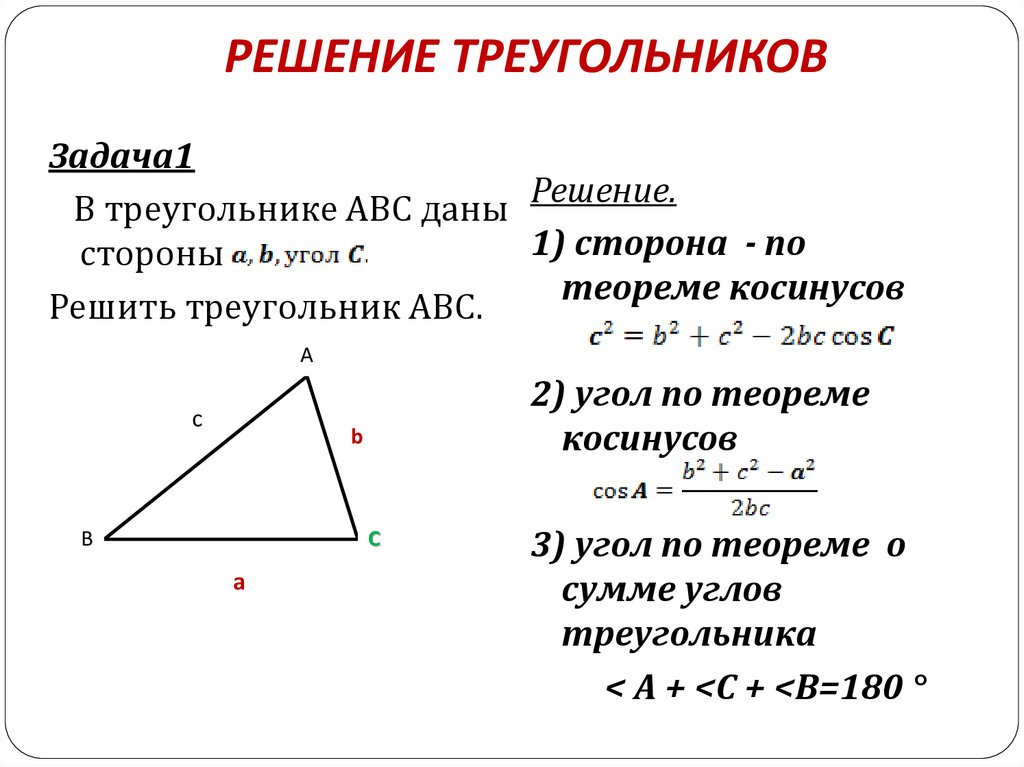
РЕШЕНИЕ ТРЕУГОЛЬНИКОВЗадача1
Решение.
В треугольнике АВС даны
1) сторона - по
стороны
теореме косинусов
Решить треугольник АВС.
А
с
2) угол по теореме
косинусов
b
В
С
а
3) угол по теореме о
сумме углов
треугольника
< А + <С + <В=180 °
7. РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
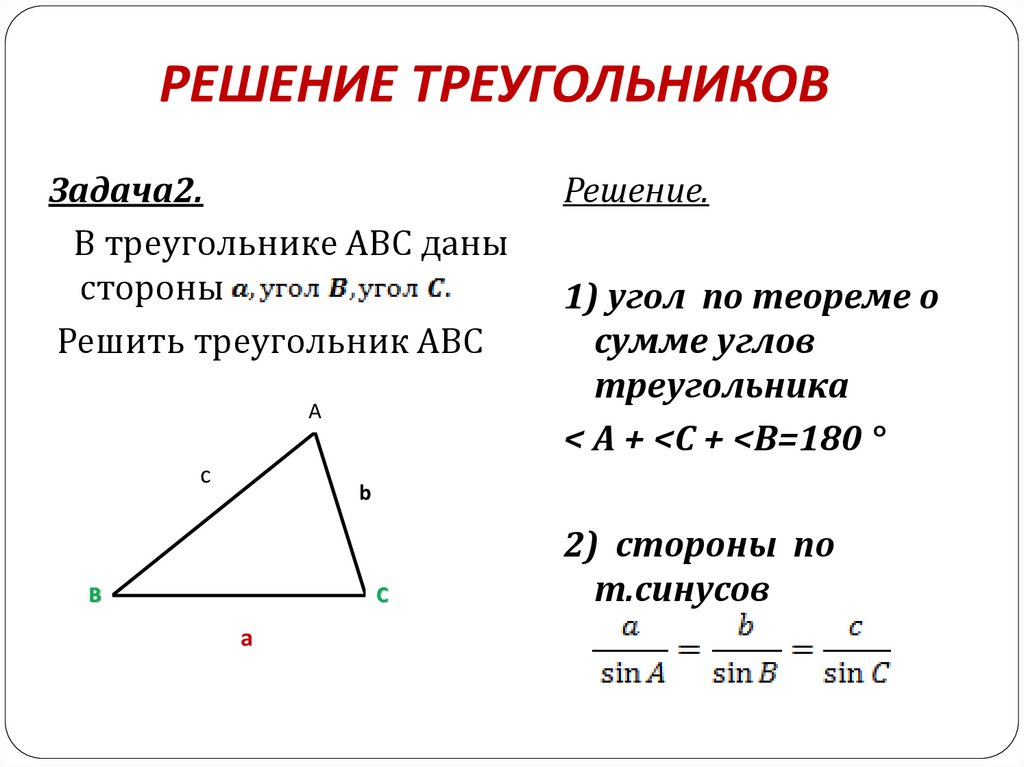
РЕШЕНИЕ ТРЕУГОЛЬНИКОВЗадача2.
В треугольнике АВС даны
стороны
Решить треугольник АВС
А
с
Решение.
1) угол по теореме о
сумме углов
треугольника
< А + <С + <В=180 °
b
В
С
а
2) стороны по
т.синусов
8. РЕШЕНИЕ ТРЕУГОЛЬНИКОВ
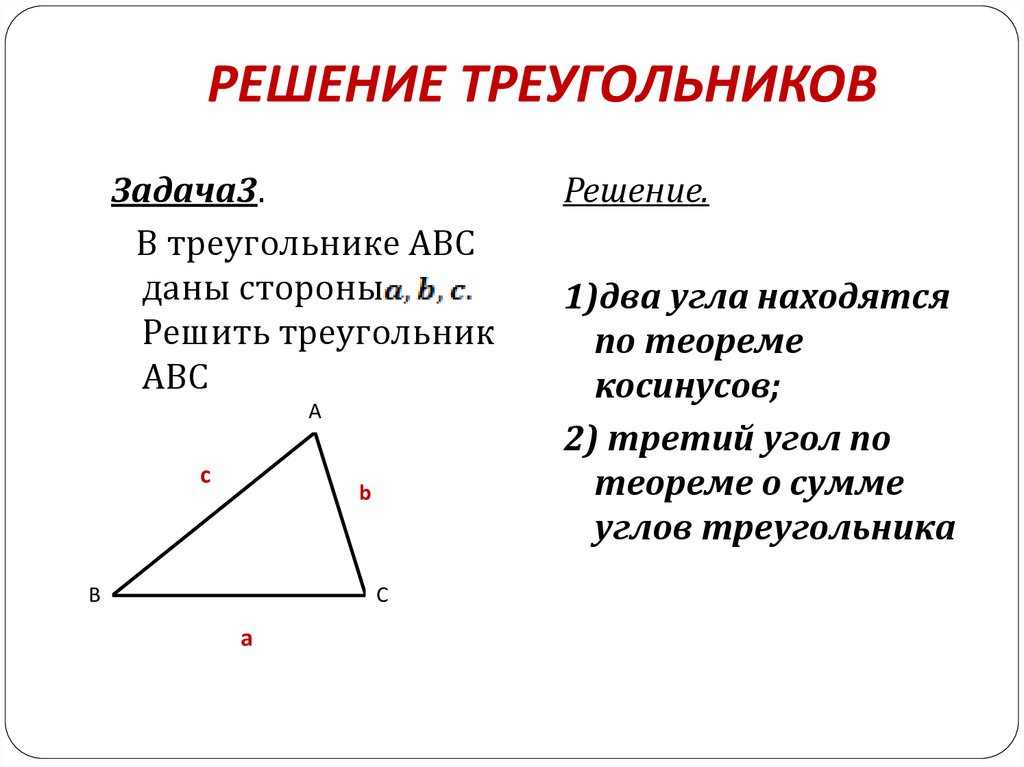
РЕШЕНИЕ ТРЕУГОЛЬНИКОВЗадача3.
В треугольнике АВС
даны стороны
Решить треугольник
АВС
А
с
b
В
С
а
Решение.
1)два угла находятся
по теореме
косинусов;
2) третий угол по
теореме о сумме
углов треугольника


 Математика
Математика








