Многогранники

1. Многогранники

2. Cправка.

Первые упоминания о многогранниках встречаются
у египтян и вавилонян за 3000 лет до нашей эры. В
то же время теория многогранников – современный
раздел математики. Теория многогранников тесно
связана со многими разделами современной
математики: топологией, теорией графов.
Многогранники интересны и сами по себе. Они
обладают богатой историей, связанной с такими
знаменитыми учеными древности как Пифагор,
Евклид, Архимед и др. Они связаны с историей
архитектуры всего мира.

3. Цели:

1.
определить понятие
многогранника;
2. рассмотреть простейшие
многогранники (параллелепипед,
куб, пирамида).

4. Проверяем тест.

«5»
– 5-6 правильных ответов.
«4» - 4 правильных ответа.
«3» – 3 правильных ответа.
«2» - 0-2 правильных ответа.

5.

Многогранникомназывается совокупность таких
плоских многоугольников,
у которых каждая сторона
одного является одновременно
стороной другого
(но только одного).

6.

Оцениваем работу в группе
(определение многогранников).
1. Точность определения понятия - 3 балла.
2. Определение элементов многогранника - 3 балла.
3. Точность изображения - 3 балла.
4. Примеры - 3 балла.

7.

Пирамида - это
многогранник, одна грань которого
многоугольник, а остальные грани треугольники с общей вершиной.
Пирамида называется правильной,
если в основании лежит правильный
многоугольник и высота пирамиды
проходит через центр многоугольника.
Пирамида называется усеченной, если
вершина её отсекается плоскостью
Тетраэдр - правильный
четырехгранник, правильная
треугольная пирамида.
Он ограничен четырьмя
равносторонними треугольниками

8.

КУБ (Гексаэдр) - правильный шестигранник .
Куб состоит из шести равных квадратов.

9.

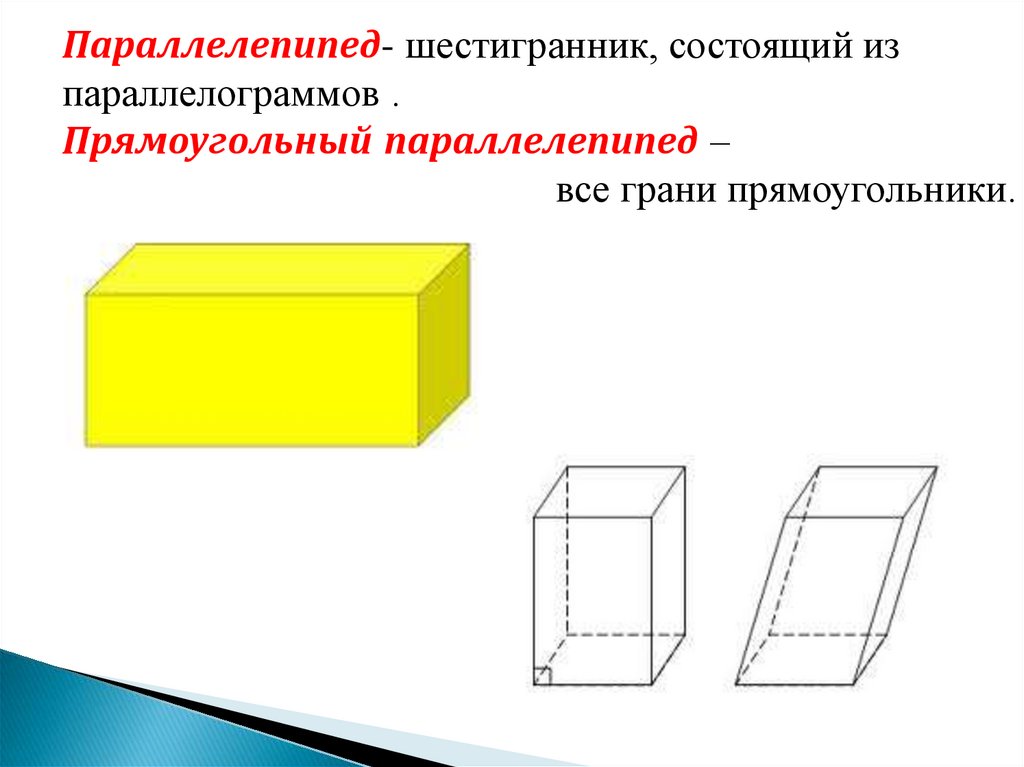
Параллелепипед- шестигранник, состоящий из
параллелограммов .
Прямоугольный параллелепипед –
параллелепипед , у которого все грани прямоугольники.

10.

Оцениваем проект группы.
1.Правильность изображения
многогранников – 5 баллов.
2. Оригинальность – 2 балла.
3. Презентация - 3 балла.

11.

Многогранники в
архитектуре.

12.

Тела Платона.
Многогранник, все грани которого
представляют собой правильные и равные
многоугольники, называют правильными
Углы при вершинах такого многогранника
равны между собой.

13.

Звездчатые формы и
соединения тел Платона.
Кроме правильных выпуклых многогранников
существуют и правильные выпукло-вогнутые многогранники.
Их называют звездчатыми (самопересекающимися).
Рассматривая пересечения продолжения граней
Платоновых тел, мы будем получать звездчатые многогранники.

14.

Оцениваем работу на
уроке.
«5»
«4»
«3»
«2»
-
25-28 баллов.
20-24 балла.
11-19 баллов.
менее 11 баллов.