Решение треугольников

1.

Презентация к уроку геометрии по теме:
«Решение треугольников»
9 класс
Симакова Наталья Борисовна
Учитель математики высшей категории
ГБОУ СОШ №264 Кировского района
Санкт-Петербург
2013

2. Решение треугольников

Урок геометрии в 9 классе
Учитель ГБОУ СОШ №264 Симакова Наталья Борисовна

3. Содержание

Соотношения между сторонами и углами в прямоугольном треугольнике
Основные соотношения в прямоугольном треугольнике
Решение прямоугольных треугольников. Задача 1
Решение прямоугольных треугольников. Задача 2
Решение задачи 2
Решение прямоугольных треугольников. Задача 3
Решение задачи 3
Теорема синусов
Теорема косинусов
Три основных типа задач на решение треугольников
Задача 4
Задача 5
Задача 6
Использованная и рекомендуемая литература
ГБОУ СОШ № 264
3

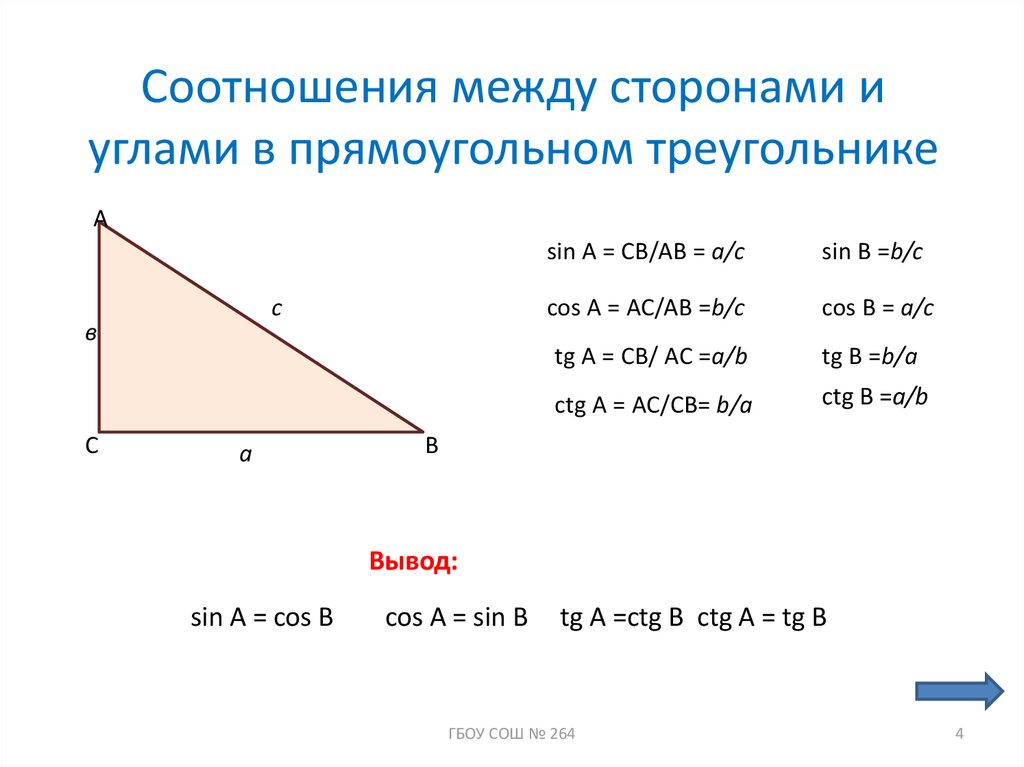
4. Cоотношения между сторонами и углами в прямоугольном треугольнике

А
с
в
С
а
sin A = CB/AB = a/c
sin B =b/c
cos A = AC/AB =b/c
cos B = a/c
tg A = CB/ AC =a/b
tg B =b/a
ctg A = AC/CB= b/a
ctg B =a/b
В
Вывод:
sin A = cos B
cos A = sin B
tg A =ctg B ctg A = tg B
ГБОУ СОШ № 264
4

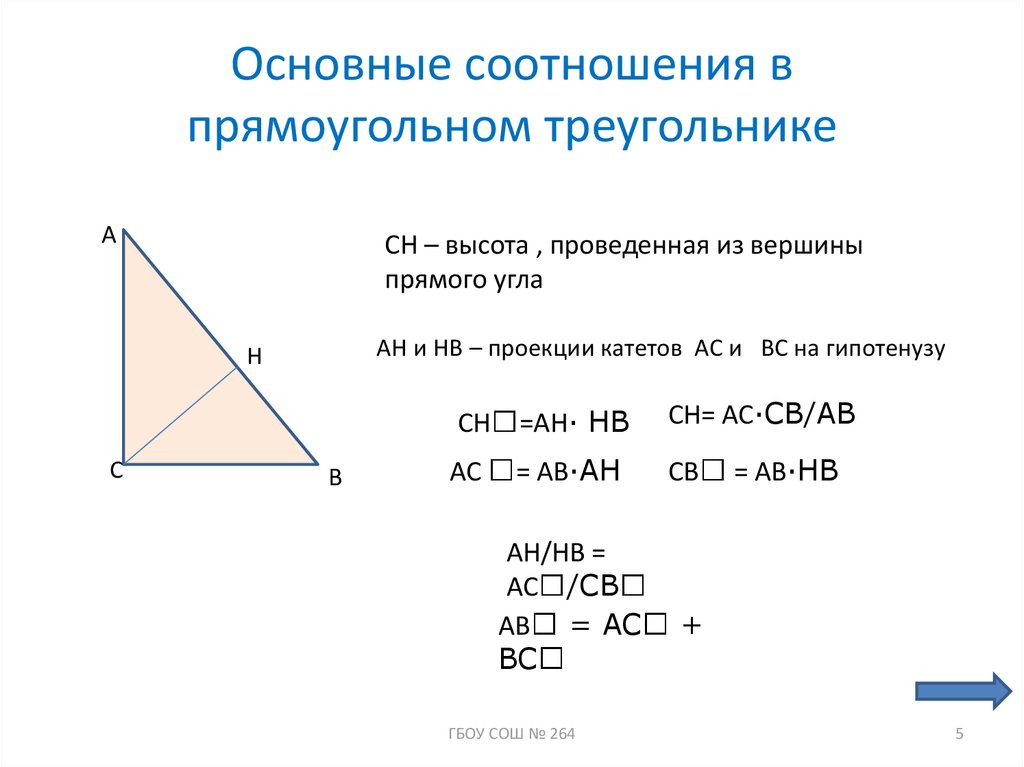
5. Основные соотношения в прямоугольном треугольнике

A
CH – высота , проведенная из вершины
прямого угла
AH и HB – проекции катетов AC и BC на гипотенузу
H
C
B
CH =AH∙ HB
CH= AC∙CB/AB
AC
CB
= AB∙AH
AH/HB =
AC /CB
AB = AC
BC
ГБОУ СОШ № 264
= AB∙HB
+
5

6. Решение прямоугольных треугольников

Задача 1
A
Дано: ∆ ABC
β
<С=90°, ВС=a, <А=β
Найти: АС, АВ, угол В.
C
a
B
Решение.
1) АВ= СВ/sinβ
AB=a/sinβ
2) AC= CB∙ ctgβ
AC=a ∙ ctgβ
3) <B= 90°-β
ГБОУ СОШ № 264
6

7. Решение прямоугольных треугольников

Задача 2
А
β
Дано: ∆ ABC
Угол С=90°, АВ=с, <А=β
с
Найти : АС, СВ, <В
С
В
ГБОУ СОШ № 264
7

8. Решение задачи 2

1) <B= 90°-β
2) АС = с∙cosβ
3) CB= c∙ sinβ
ГБОУ СОШ № 264
8

9. Решение прямоугольных треугольников

Задача 3
А
Дано: ∆ ABC
АС = в, СВ = а
Найти: АВ,<А,<В
в
С
а
В
ГБОУ СОШ № 264
9

10. Решение задачи 3

1)АВ
=a
+b
2)tgA =BC/AC
3) tgB= AC/BC
ГБОУ СОШ № 264
10

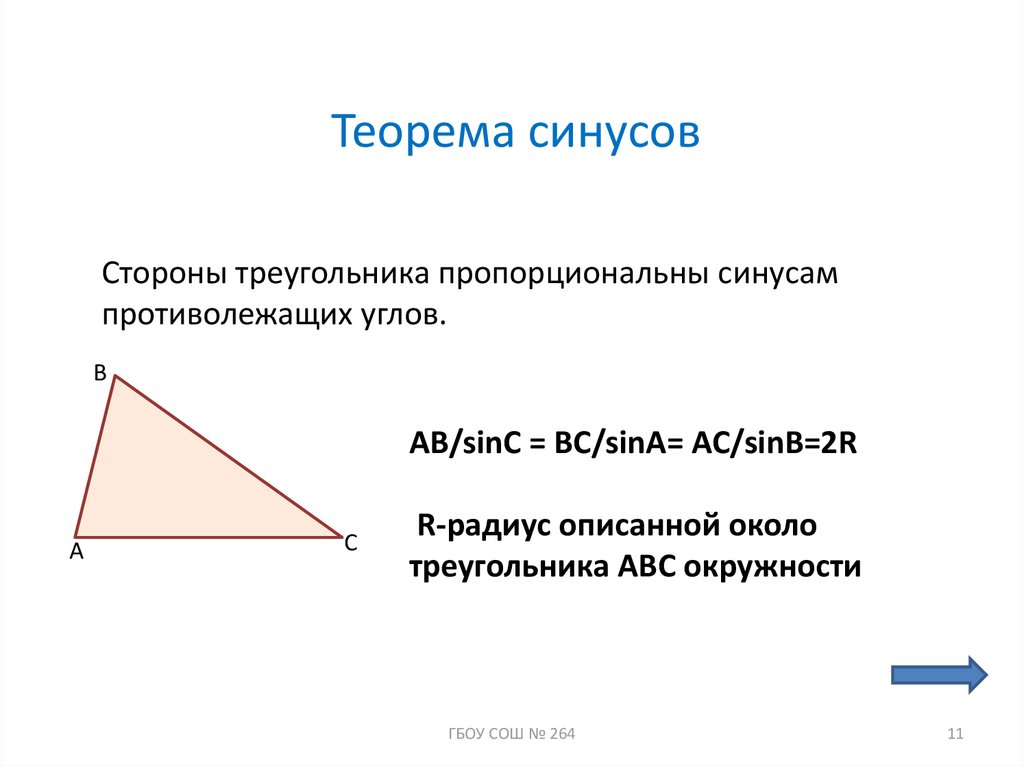
11. Теорема синусов

Стороны треугольника пропорциональны синусам
противолежащих углов.
B
AB/sinC = BC/sinA= AC/sinB=2R
A
C
R-радиус описанной около
треугольника АВС окружности
ГБОУ СОШ № 264
11

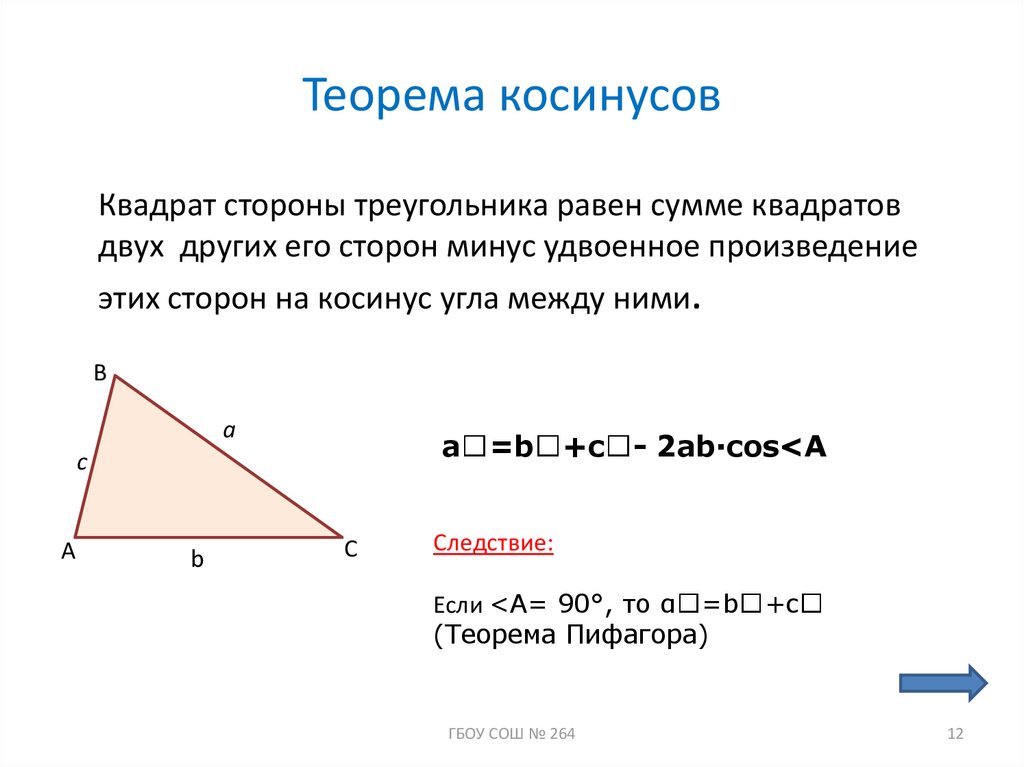
12. Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов
двух других его сторон минус удвоенное произведение
этих сторон на косинус угла между ними.
B
a
a
c
A
b
C
=b
+c - 2ab∙cos<A
Следствие:
Если <A= 90°, то α =b +c
(Теорема Пифагора)
ГБОУ СОШ № 264
12

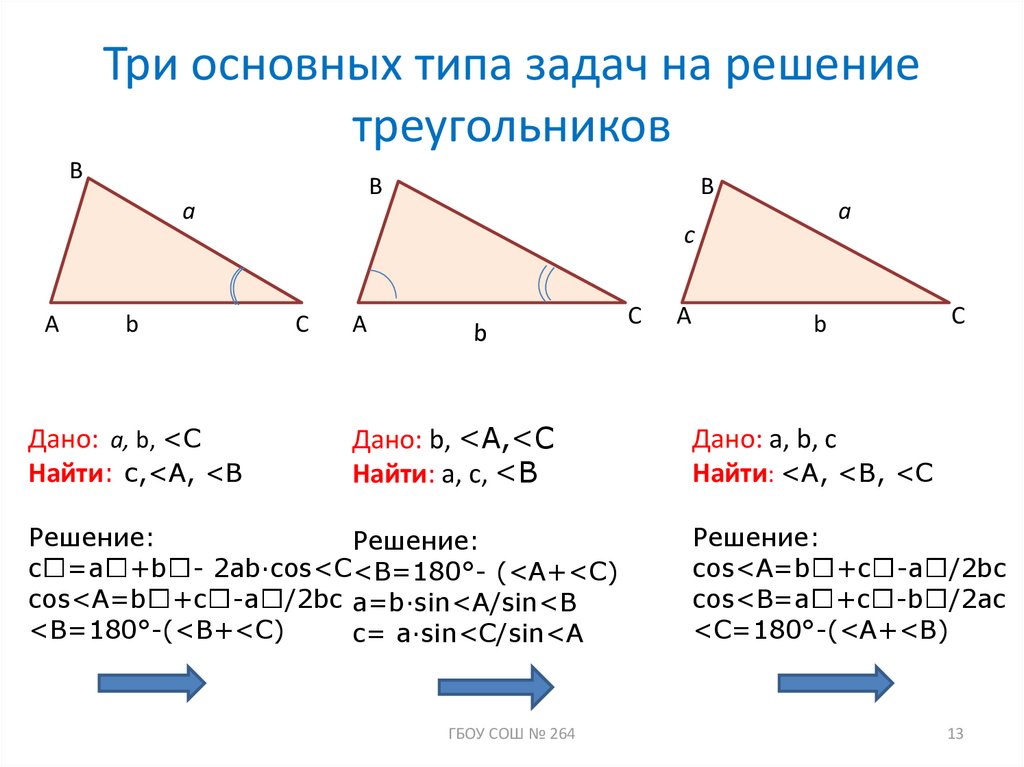
13. Три основных типа задач на решение треугольников

B
B
a
A
b
Дано: a, b, <C
Найти: с,<A, <B
B
a
c
C
C
A
Дано: b, <A,<C
Найти: a, c, <B
Решение:
Решение:
c =a +b - 2ab∙cos<C <B=180°- (<A+<C)
cos<A=b +c -a /2bc a=b∙sin<A/sin<B
<B=180°-(<B+<C)
c= a∙sin<C/sin<A
ГБОУ СОШ № 264
A
b
C
Дано: a, b, c
Найти: <A, <B, <C
Решение:
cos<A=b +c -a /2bc
cos<B=a +c -b /2ac
<C=180°-(<A+<B)
13

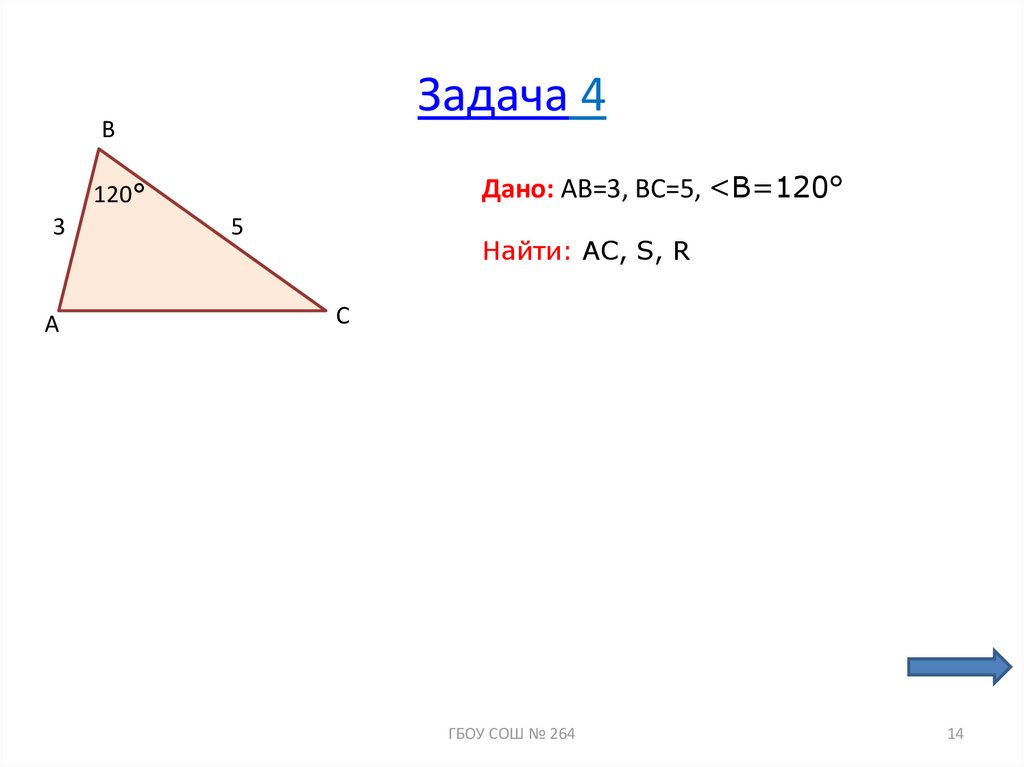
14. Задача 4

B
Дано: AB=3, BC=5, <B=120°
120°
3
A
5
Найти: АС, S, R
C
ГБОУ СОШ № 264
14

15. Задача 5

B
40°
Дано: <A=60°, <B=40°, c=14
14
Найти: a, b,<C
60°
A
C
ГБОУ СОШ № 264
15

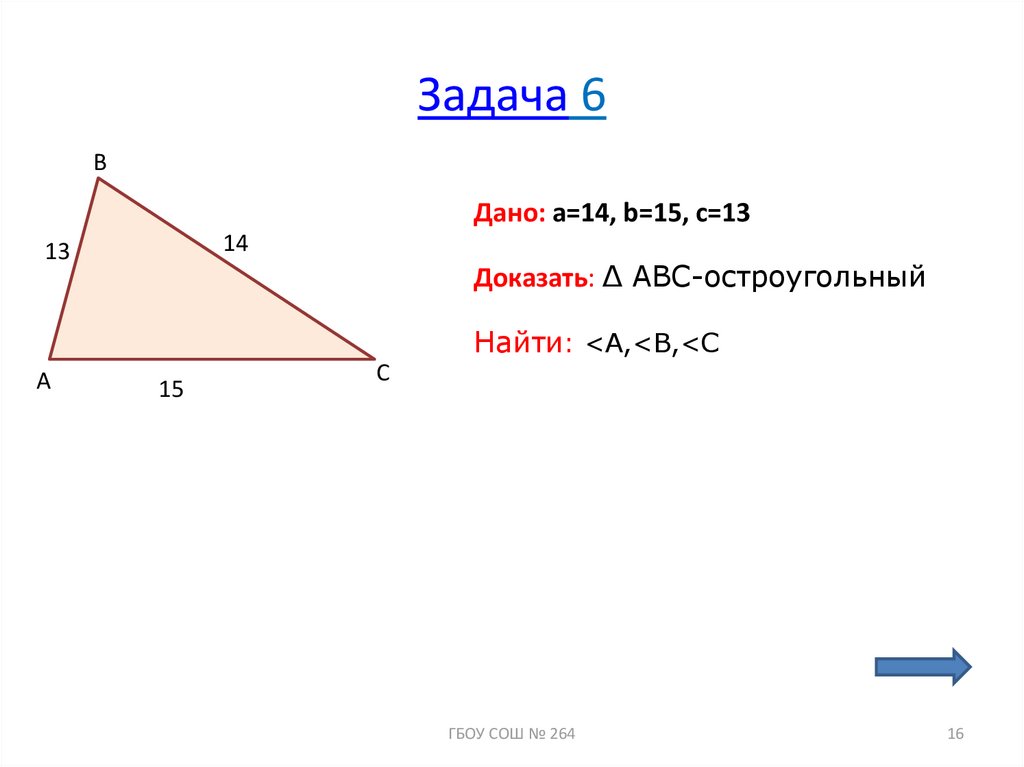
16. Задача 6

B
Дано: a=14, b=15, c=13
14
13
Доказать: ∆ ABC-остроугольный
Найти: <A,<B,<C
A
15
C
ГБОУ СОШ № 264
16

17. Использованная и рекомендуемая литература

1.
«Геометрия 7-9: учебник для общеобразовательных учреждений»
авт.: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г.Позняк,
И.И. Юдина, Москва «Просвещение»,2010 г
2. «Задачи к урокам геометрии 7-11 класс» , авт.: Зив Б.Г. ,СанктПетербург, НПО «Мир и семья», изд-во «Акация», 2005 г
3. «Задачи по геометрии 7-11», авт.: Б.Г. Зив, В.М.Мейлер,
А.Г. Баханский, Москва «Просвещение», 2000 г
4. «Изучение геометрии в 7-9 классах. Методические рекомендации к
учебнику», авт.: Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков, В.Б.
Некрасов, И.И. Юдина, Москва, « Просвещение», 1997 г
ГБОУ СОШ № 264
17