Похожие презентации:
Теория систем счисления
1. Теория систем счисления
2. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
Для записи целого двоичного числа всистеме с основанием q=2n достаточно
данное двоичное число разбить на грани
справа налево (т.е. от младших разрядов к
старшим) по n цифр в каждой грани. Затем
каждую грань следует рассматривать как
n-разрядное двоичное число и записать
его как цифру в системе с основанием
q=2n.
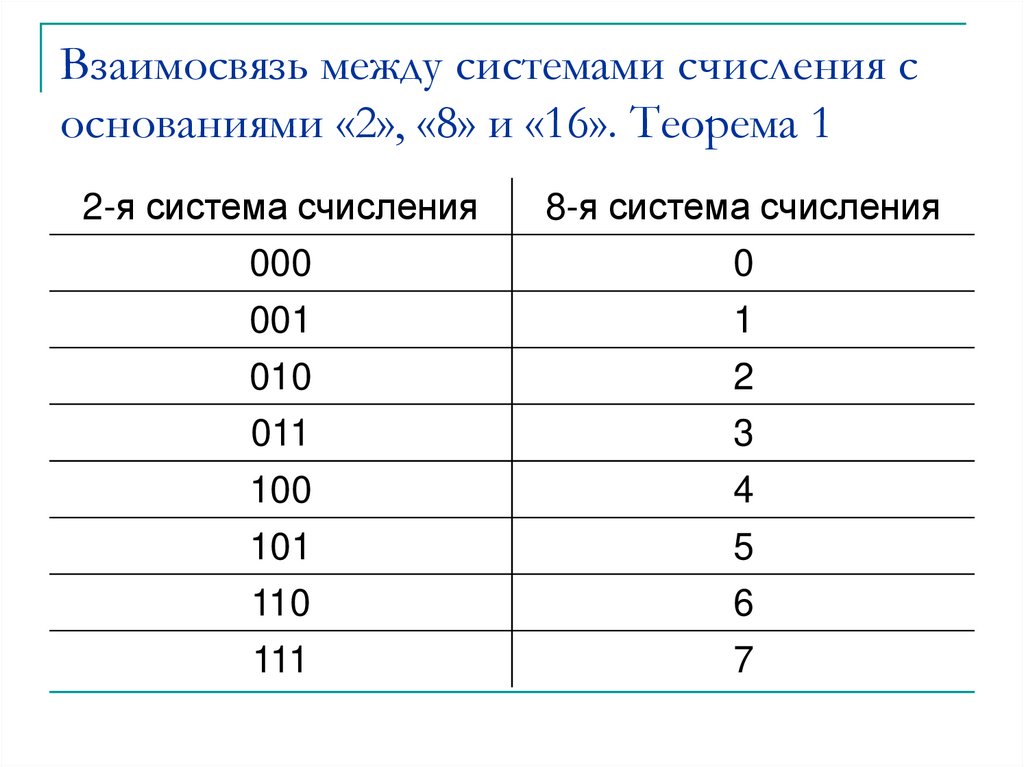
3. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
2-я система счисления8-я система счисления
000
0
001
1
010
2
011
3
100
4
101
5
110
6
111
7
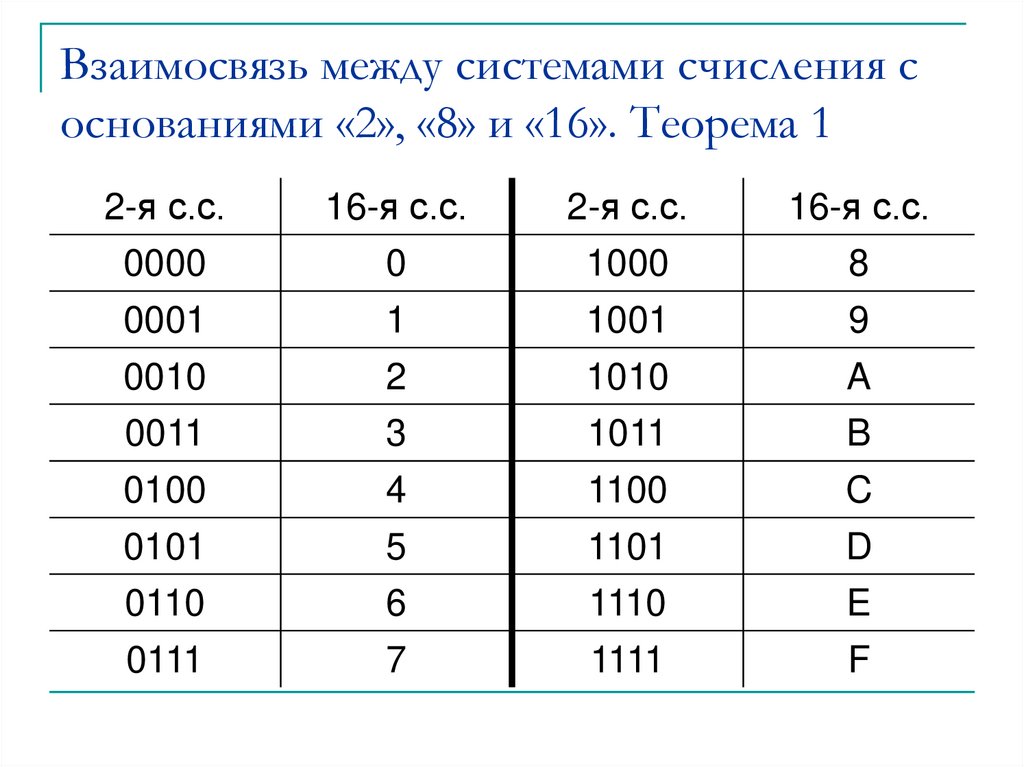
4. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
2-я с.с.16-я с.с.
2-я с.с.
16-я с.с.
0000
0
1000
8
0001
1
1001
9
0010
2
1010
A
0011
3
1011
B
0100
4
1100
C
0101
5
1101
D
0110
6
1110
E
0111
7
1111
F
5. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
Создайте подобную таблицу перевода длячетверичной системы счисления.
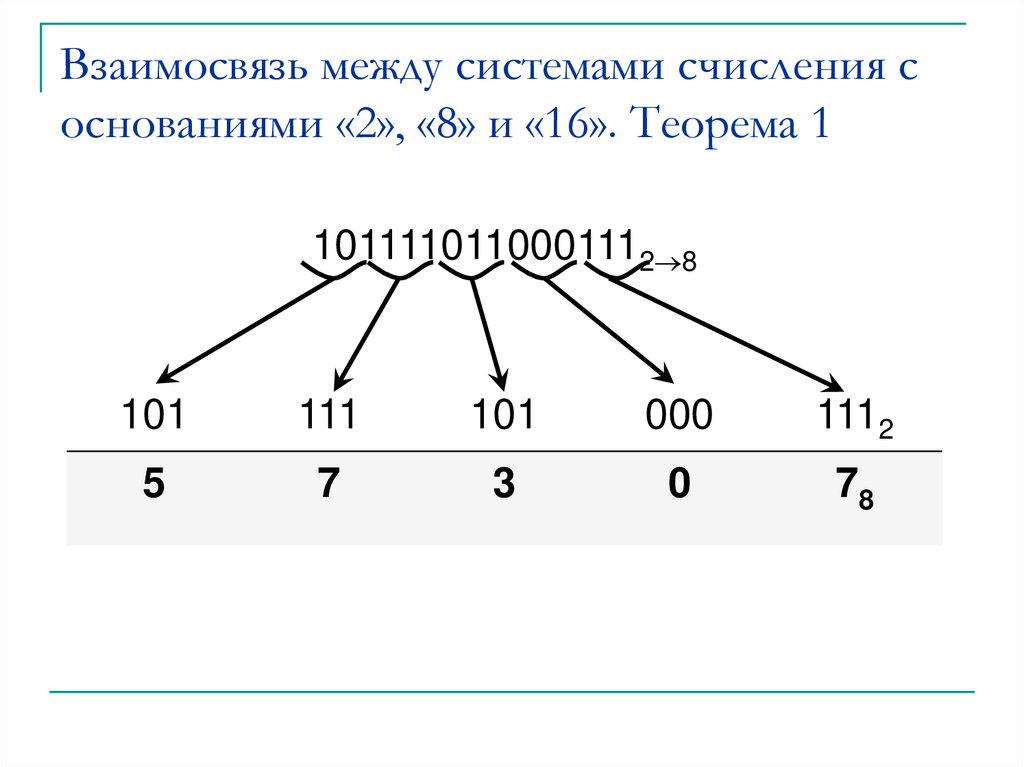
6. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
1011110110001112 8101
111
101
000
1112
5
7
3
0
78
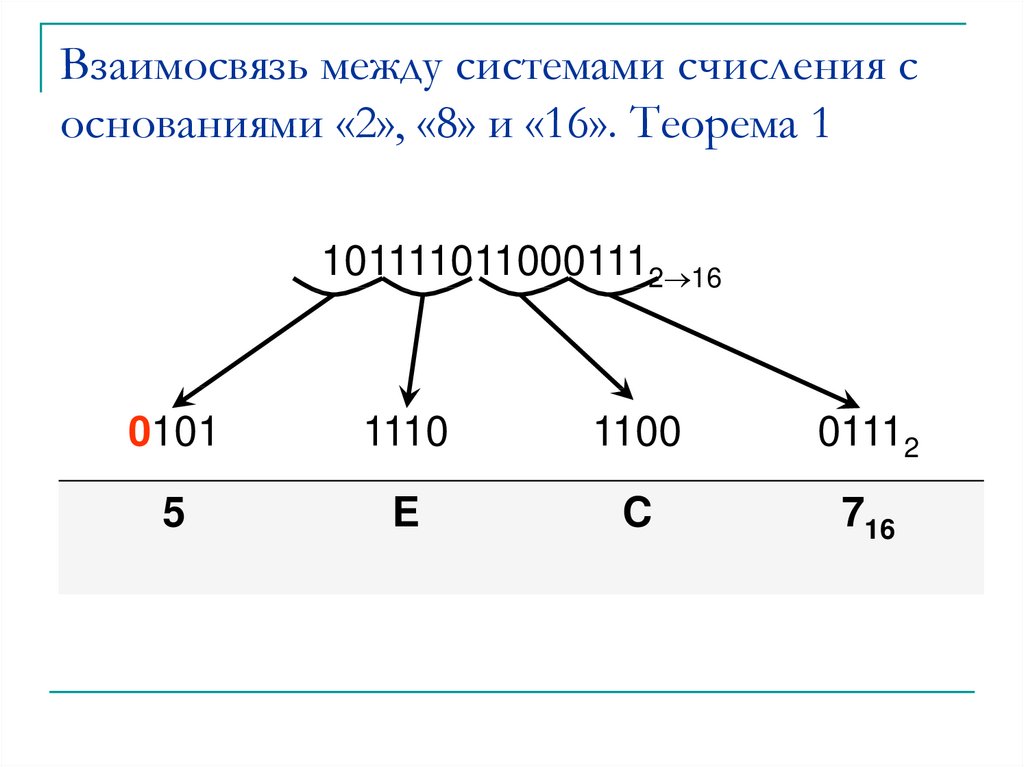
7. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 1
1011110110001112 160101
1110
1100
01112
5
E
C
716
8. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 2
Для замены целого числа, записанного всистеме счисления с основанием p=2n,
равным ему числом в двоичной системе
счисления, достаточно каждую цифру
данного числа заменить n-разрядным
двоичным числом.
9. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 2
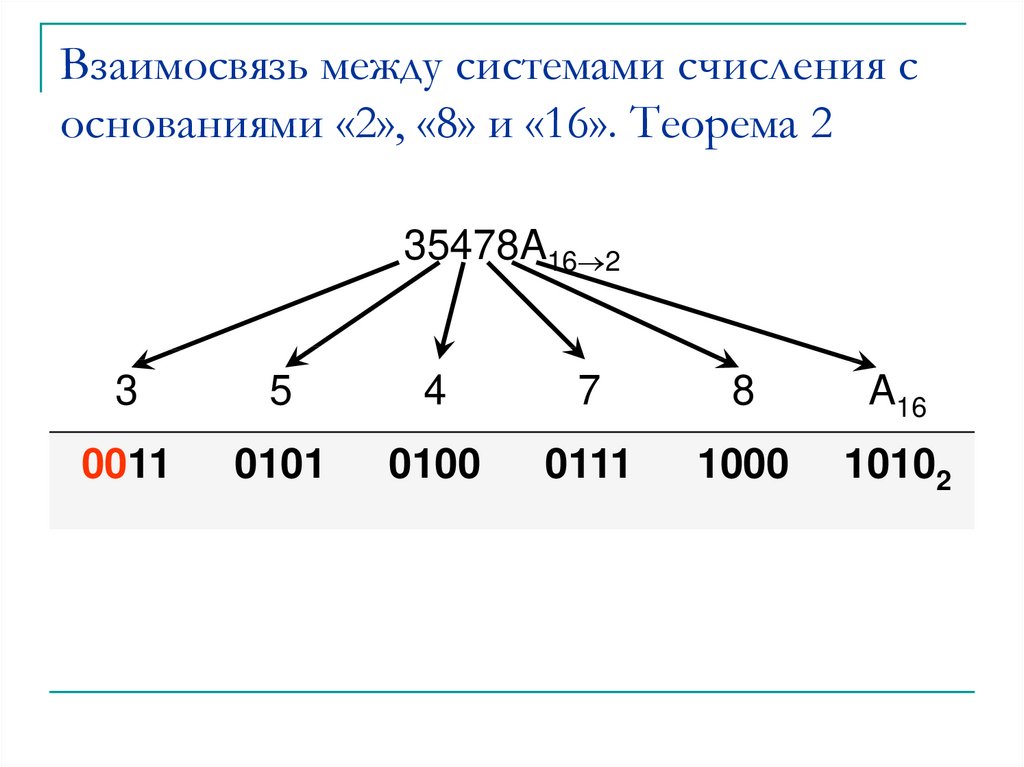
35478A16 23
5
4
7
8
A16
0011
0101
0100
0111
1000
10102
10. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 2
60128 26
0
1
28
110
000
001
0102
11. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 3
Для перевода правильных двоичныхдробей в систему счисления с основанием
q=2n необходимо данную дробь разбить на
грани слева направо от запятой по n цифр
в каждой. Затем каждую грань следует
рассматривать как n-разрядное двоичное
число и записать его как цифру в системе
счисления с основанием q=2n.
12. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 3
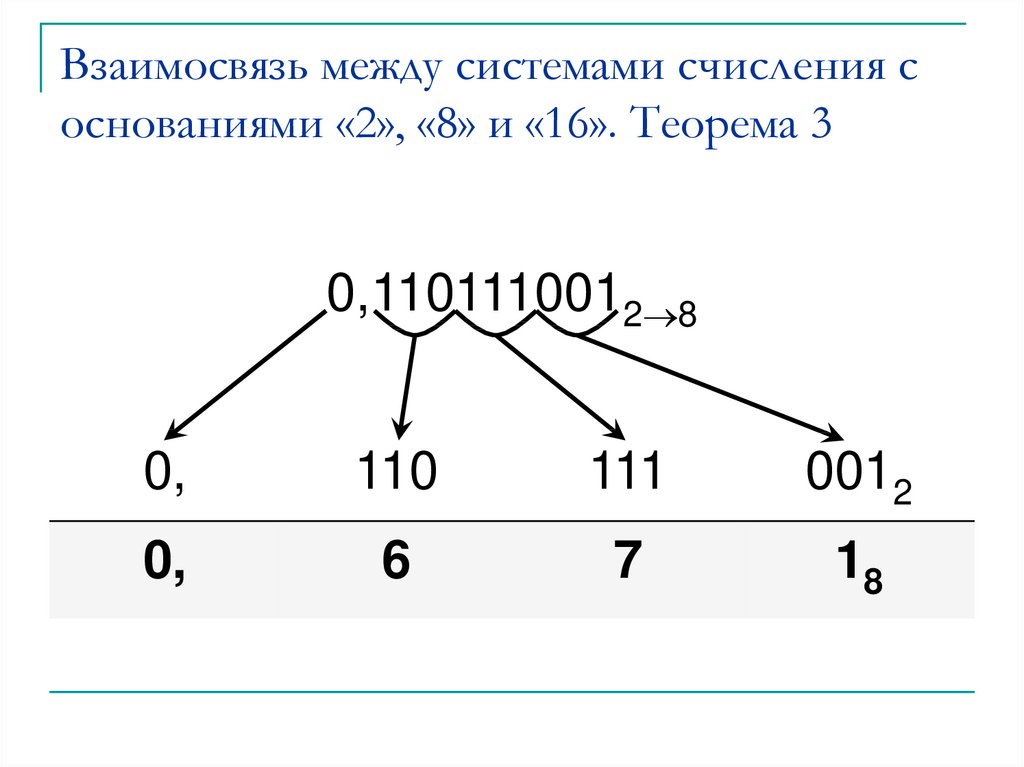
0,1101110012 80,
110
111
0012
0,
6
7
18
13. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 3
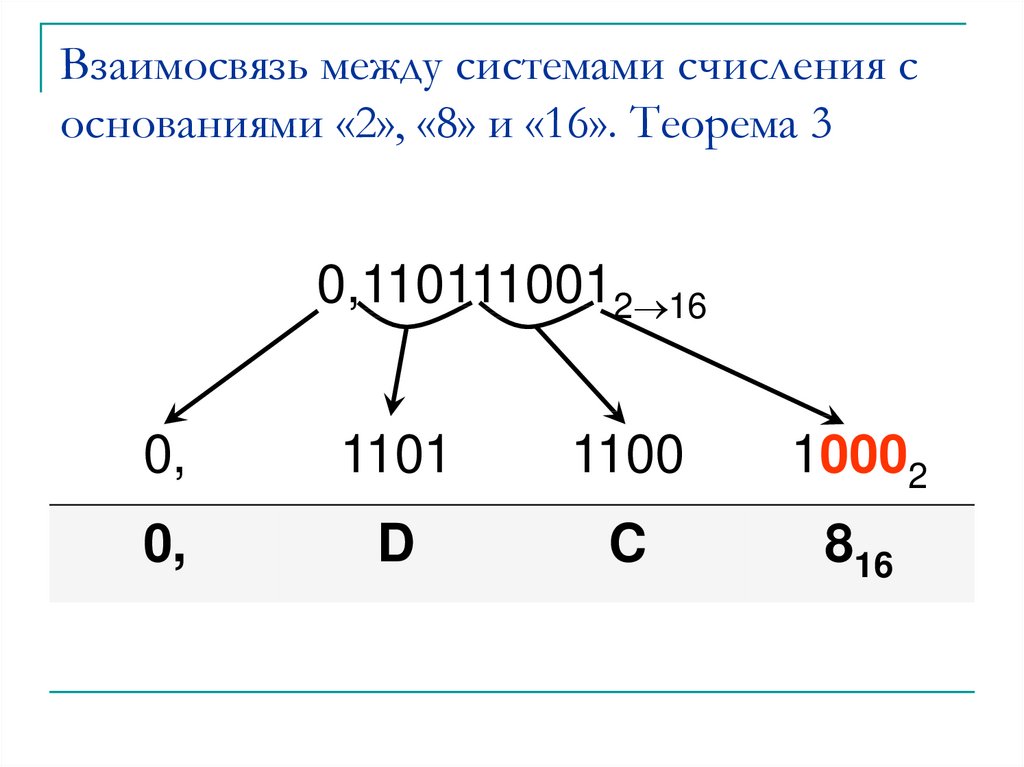
0,1101110012 160,
1101
1100
10002
0,
D
C
816
14. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 4
Для замены правильной дроби,записанной в системе счисления с
основанием p=2n, равной ей дробью в
двоичной системе счисления достаточно
каждую цифру данной дроби заменить nразрядным двоичным числом.
15. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 4
0,A3116 20,
A
3
116
0,
1010
0011
00012
16. Взаимосвязь между системами счисления с основаниями «2», «8» и «16». Теорема 4
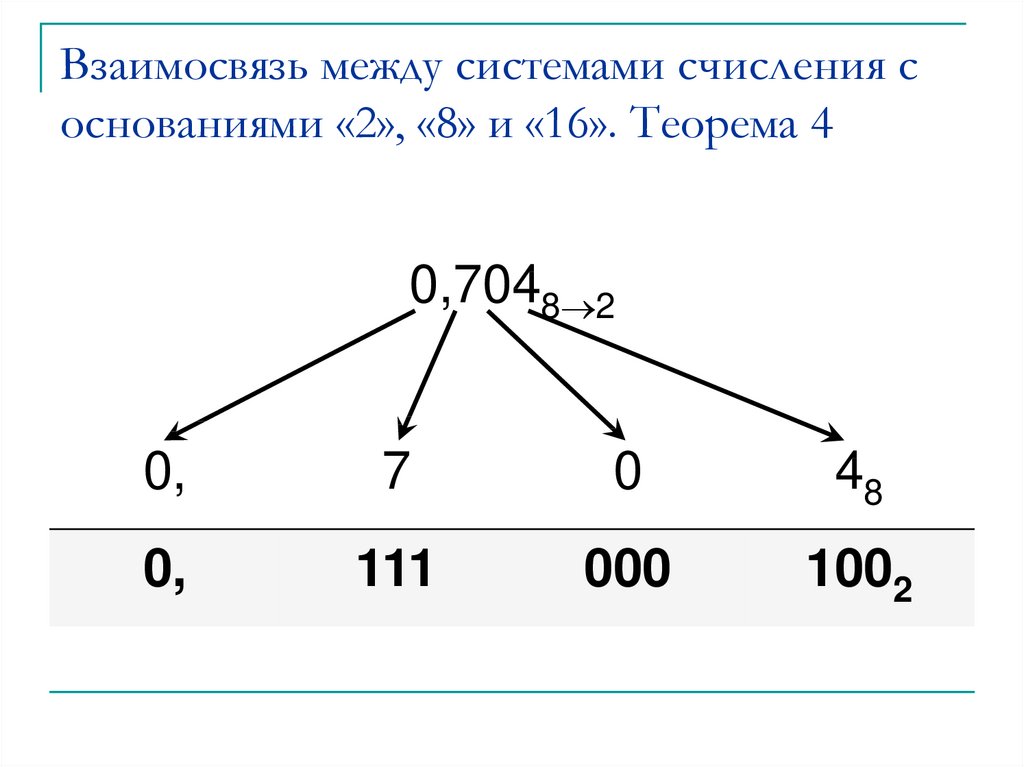
0,7048 20,
7
0
48
0,
111
000
1002
17. Взаимосвязь между системами счисления с основаниями «2», «8» и «16»
Подумайте, будут ли правомочныподобные теоремы для систем счисления
с основаниями 3, 9, 27.
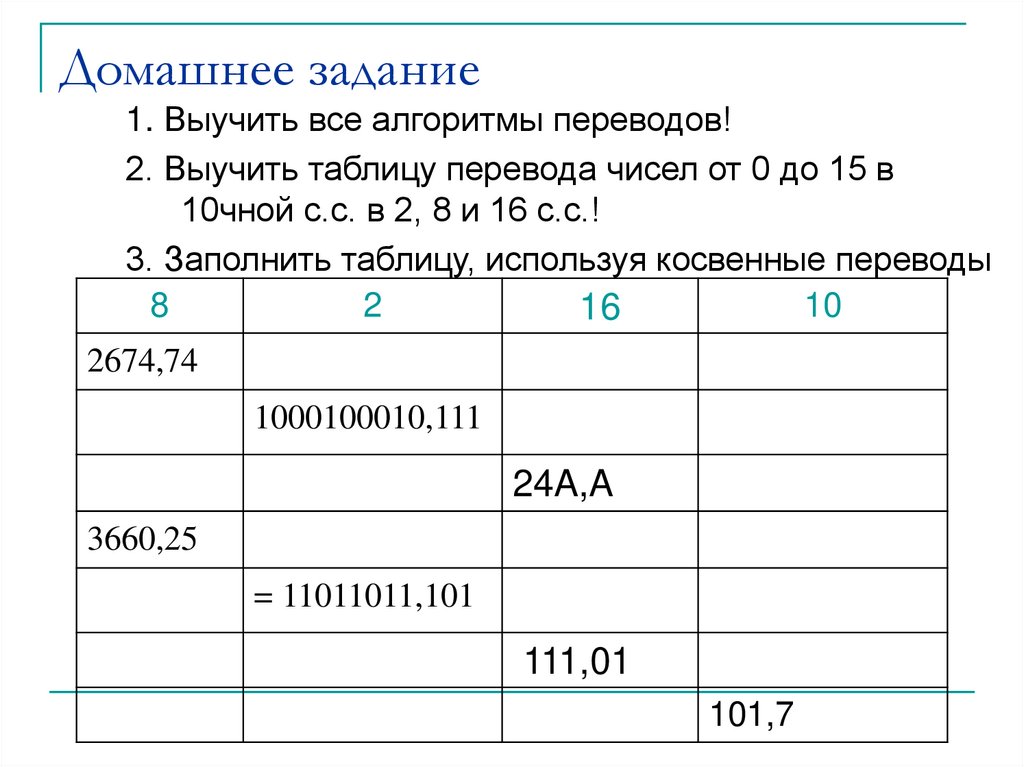
18. Домашнее задание
1. Выучить все алгоритмы переводов!2. Выучить таблицу перевода чисел от 0 до 15 в
10чной с.с. в 2, 8 и 16 с.с.!
3. Заполнить таблицу, используя косвенные переводы
8
2
10
16
2674,74
1000100010,111
24A,A
3660,25
= 11011011,101
111,01
101,7









 Информатика
Информатика








