Элементы финансовой математики. Основы финансовых вычислений. Лекция 1

1. Основы финансовых вычислений

ОСНОВЫ
ФИНАНСОВЫХ
ВЫЧИСЛЕНИЙ
Элементы
финансовой
математики

2. Литература:

ЛИТЕРАТУРА:
10.03.2019
Четыркин Е.М. Финансовая математика:
учебник. М., 2011. – 392 с.
Мелкумов Я.С. Финансовые вычисления:
теория и практика: учебно-справочное пособие.
М., 2012. – 408 с.
Левин Л.А. Финансовая математика: учебнометод. пособие. М., 2006. – 111 с.
Основы финансовых вычислений
2

3. Предмет финансовой математики

ПРЕДМЕТ ФИНАНСОВОЙ МАТЕМАТИКИ
10.03.2019
Финансовая математика – это модели и
алгоритмы финансовых расчетов.
Базовой финансовой операцией является
кредитование.
Субъекты рынка заключают сделку: кредитор
выдает заемщику ссуду с условием, что в
установленный срок заемщик вернет
кредитору ссуду с наращением (процентами).
Основы финансовых вычислений
3

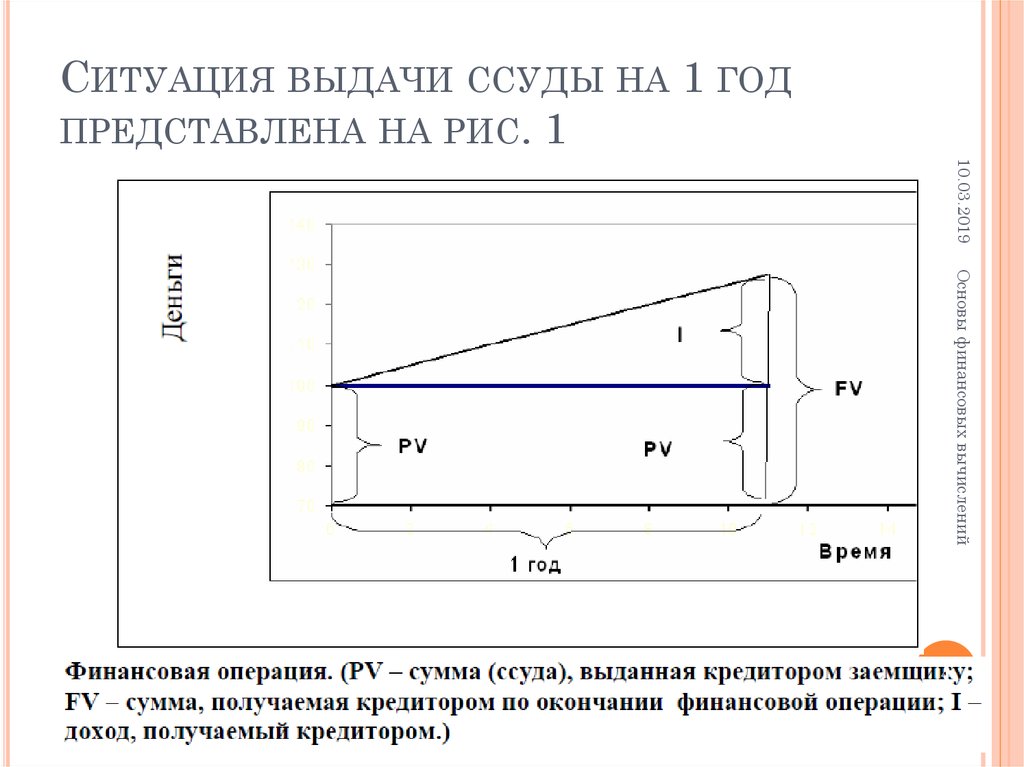
4. Ситуация выдачи ссуды на 1 год представлена на рис. 1

СИТУАЦИЯ ВЫДАЧИ ССУДЫ НА 1 ГОД
ПРЕДСТАВЛЕНА НА РИС. 1
10.03.2019
Основы финансовых вычислений
4

5. Таким образом:

ТАКИМ ОБРАЗОМ:
10.03.2019
1. Финансовая математика представляет собой
совокупность методов определения изменения
стоимости денег, происходящего вследствие их
возвратного движения в процессе воспроизводства.
2. Финансовая математика – это раздел
количественного анализа финансовых операций,
предметом которого является изучение
функциональных зависимостей между параметрами
коммерческих сделок или финансово-банковских
операций и разработка на их основе методов
решения финансовых задач определенного класса.
Основы финансовых вычислений
5

6. Объект финансовой математики

ОБЪЕКТ ФИНАНСОВОЙ МАТЕМАТИКИ
10.03.2019
Основы финансовых вычислений
Объектом изучения финансовой математики
является финансовая операция, в которой
необходимость использования финансовоэкономических вычислений возникает всякий
раз, когда в условиях сделки (финансовой
операции) прямо или косвенно присутствуют
временные параметры: даты, сроки выплат,
периодичность поступления денежных средств,
отсрочка платежей и т.д.
6

7. Задачи финансовой математики:

ЗАДАЧИ ФИНАНСОВОЙ МАТЕМАТИКИ:
10.03.2019
измерение конечных финансовых результатов
операции (сделки, контракта) для каждой из
участвующих сторон;
разработка планов выполнения финансовых
операций, в том числе планов погашения
задолженности;
измерение зависимости конечных результатов
операции от основных ее параметров;
определение допустимых критических
значений этих параметров и расчет
параметров эквивалентного (безубыточного)
изменения первоначальных условий операции.
Основы финансовых вычислений
7

8. Фактор времени в финансово-экономических расчетах

ФАКТОР ВРЕМЕНИ В ФИНАНСОВОЭКОНОМИЧЕСКИХ РАСЧЕТАХ
10.03.2019
Основы финансовых вычислений
В финансово-экономических расчетах фактор
времени играет наиболее важную роль в сравнении
со стоимостными характеристиками финансовой
операции.
Именно время определяет конечный финансовый
результат.
Важность учета фактора времени обусловлена
принципом неравноценности денег, относящихся к
различным моментам времени: равные по
абсолютной величине денежные суммы «сегодня» и
«завтра» оцениваются по-разному: сегодняшние
8
деньги ценнее будущих.

9. Зависимость ценности денег от времени обусловлена влиянием фактора времени:

ЗАВИСИМОСТЬ ЦЕННОСТИ ДЕНЕГ ОТ
ВРЕМЕНИ ОБУСЛОВЛЕНА ВЛИЯНИЕМ
1. деньги можно продуктивно использовать во
времени как приносящий доход финансовый
актив, т.е. деньги могут быть инвестированы и
тем самым приносить доход.
2. инфляционные процессы ведут в
обесцениванию денег во времени (сегодня на
рубль можно купить товара больше, чем завтра
на этот же рубль, т.к. цены на товары
повысятся).
3. неопределенность будущего и связанный с
этим риск повышает ценность имеющихся
денег (сегодня рубль в руке уже есть и его
можно израсходовать на потребление, а будет
ли он завтра – еще вопрос).
10.03.2019
ФАКТОРА ВРЕМЕНИ:
Основы финансовых вычислений
9

10.

Для корректировки арифметического
сопоставления величин разновременных
затрат/доходов используются финансовые
коэффициенты, основанные на формулах
начисления процентов, приводят к одному и тому
же моменту времени.
Приведение более ранней суммы к
эквивалентной ей величине в другой момент
времени в будущем производится путем
умножения на коэффициент наращения.
Начисление процентов производится дискретно
за фиксированные одинаковые интервалы
времени («периоды начисления»).
Период начисления – это отрезок времени между
двумя следующими друг за другом процедурами
взимания процентов.
10.03.2019
Основы финансовых вычислений
10

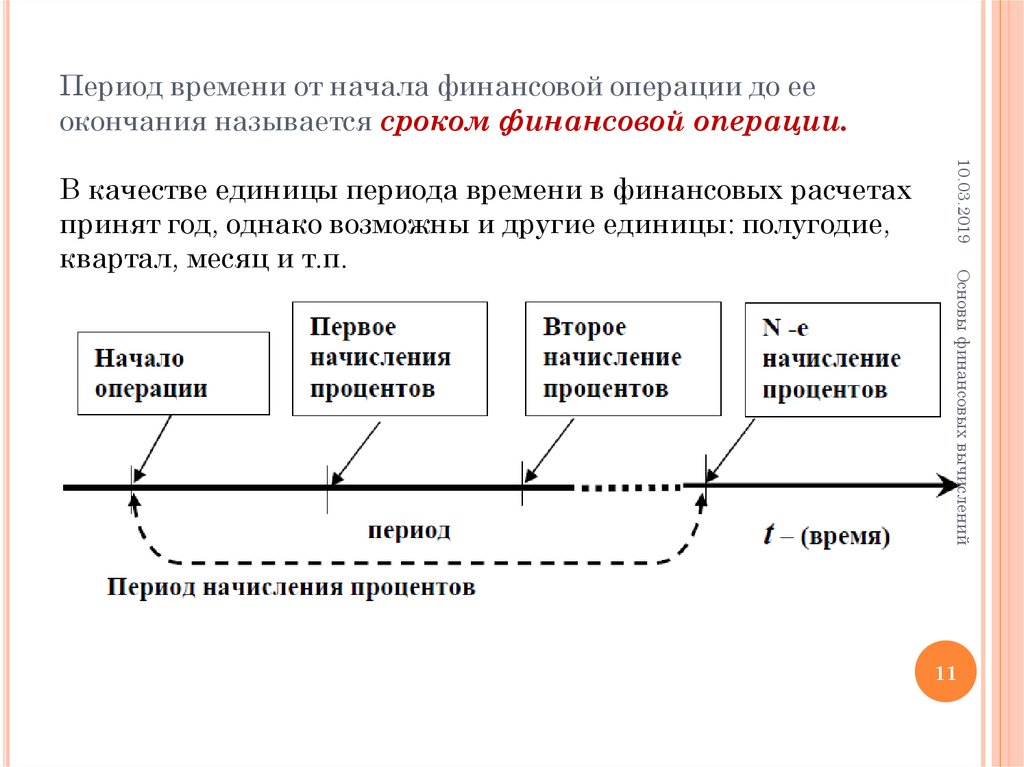
11. Период времени от начала финансовой операции до ее окончания называется сроком финансовой операции. В качестве единицы периода

Период времени от начала финансовой операции до ее
окончания называется сроком финансовой операции.
10.03.2019
Основы финансовых вычислений
В качестве единицы периода времени в финансовых расчетах
принят год, однако возможны и другие единицы: полугодие,
квартал, месяц и т.п.
11

12. 1.1. Изменение стоимости вложений за счет присоединения процентов

1.1. ИЗМЕНЕНИЕ СТОИМОСТИ ВЛОЖЕНИЙ
ЗА СЧЕТ ПРИСОЕДИНЕНИЯ ПРОЦЕНТОВ
10.03.2019
Основы финансовых вычислений
Рассмотрим процесс наращения, т.е.
определения денежной суммы в будущем,
исходя из заданной суммы сейчас.
Экономический смысл операции наращения
состоит в определении величины той суммы,
которой будет или желает располагать
инвестор по окончании этой операции.
Здесь идет движение денежного потока от
настоящего к будущему.
12

13.

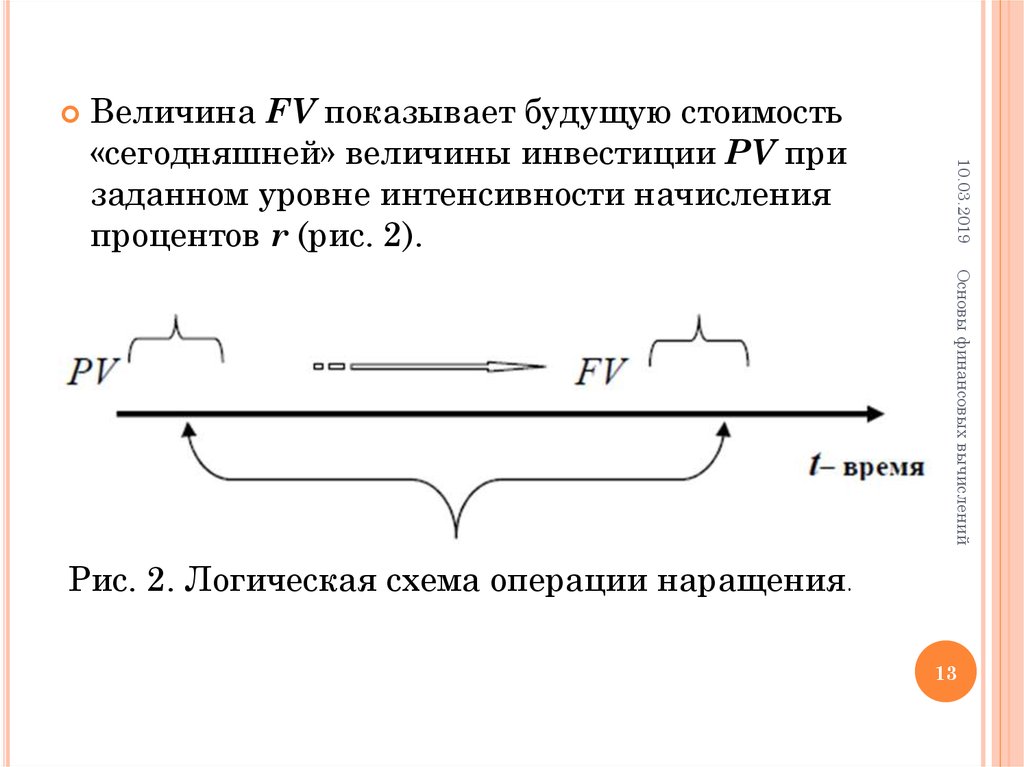
10.03.2019
Величина FV показывает будущую стоимость
«сегодняшней» величины инвестиции PV при
заданном уровне интенсивности начисления
процентов r (рис. 2).
Основы финансовых вычислений
Рис. 2. Логическая схема операции наращения.
13

14.

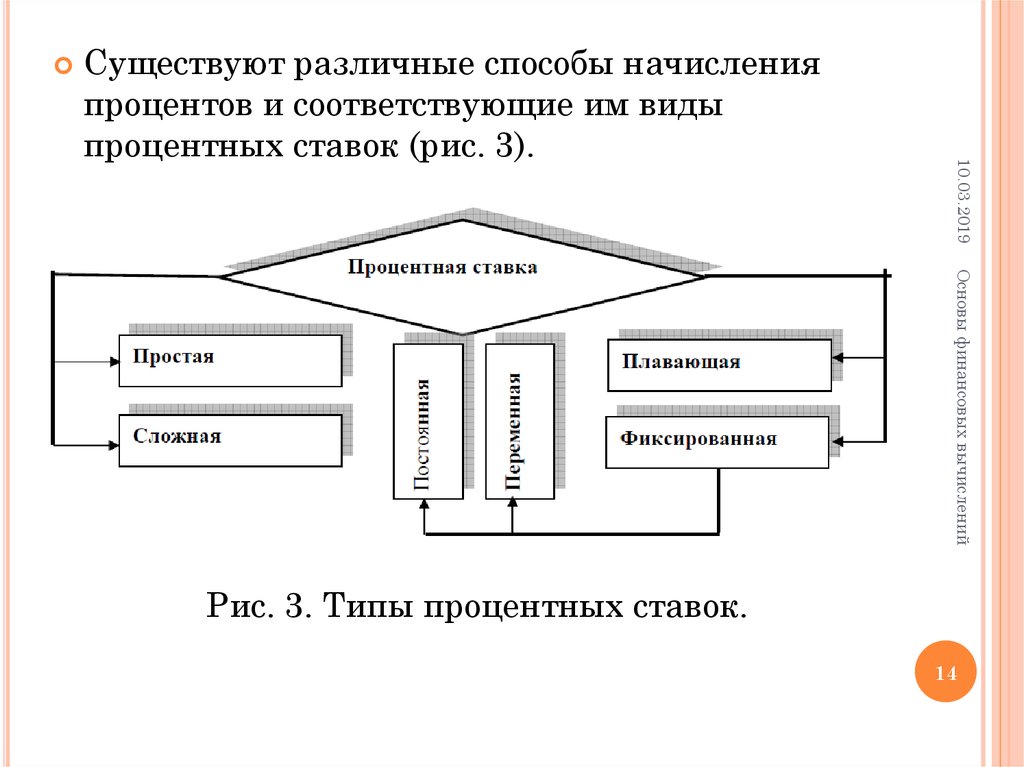
10.03.2019
Существуют различные способы начисления
процентов и соответствующие им виды
процентных ставок (рис. 3).
Основы финансовых вычислений
Рис. 3. Типы процентных ставок.
14

15. Характеристика типов процентных ставок

ХАРАКТЕРИСТИКА ТИПОВ ПРОЦЕНТНЫХ СТАВОК
Сложная процентная ставка –
применяется к наращенной сумме долга, т.е. к
сумме, увеличенной на величину начисленных
за предыдущий период процентов (таким
образом, исходная база постоянно
увеличивается).
Основы финансовых вычислений
Простая процентная ставка –
применяется к одной и той же первоначальной
сумме долга на протяжении всего срока ссуды,
т.е. исходная база (денежная сумма) всегда
одна и та же.
10.03.2019
15

16.

ХАРАКТЕРИСТИКА ТИПОВ ПРОЦЕНТНЫХ СТАВОК
10.03.2019
Основы финансовых вычислений
Плавающая процентная ставка – ставка,
привязанная к определенной величине,
изменяющейся во времени, включая надбавку
к ней (маржу), которая определяется целым
рядом условий (сроком операции и т.д.). Основу
процентной ставки составляет базовая ставка,
которая является начальной величиной.
Фиксированная процентная ставка –
ставка, зафиксированная в виде определенного
числа (суммы) в финансовых контрактах.
16

17.

ХАРАКТЕРИСТИКА ТИПОВ ПРОЦЕНТНЫХ СТАВОК
Переменная процентная ставка –
дискретно изменяющаяся во времени, но
имеющая конкретную числовую
характеристику.
Основы финансовых вычислений
Постоянная процентная ставка –
неизменная на протяжении всего периода
ссуды.
10.03.2019
17

18. 1.2. Основные категории финансово-экономических расчетов

1.2. ОСНОВНЫЕ КАТЕГОРИИ ФИНАНСОВОЭКОНОМИЧЕСКИХ РАСЧЕТОВ
Основы финансовых вычислений
В любой простейшей финансовой операции
всегда присутствуют четыре величины:
время (n);
современная величина (PV);
наращенная или будущая величина (FV);
процентная ставка (r).
10.03.2019
В финансовой математике широко представлены
все виды статистических показателей:
абсолютные, относительные и средние величины.
18

19. Основные обозначения:

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ:
Традиционно в финансовых расчетах время
измеряется в годах, а процентная ставка берется
годовая, хотя возможны и другие измерители
времени – квартал, месяц, день и т.п.
Все эти условия оговариваются в договоре о
предоставлении кредита.
Основы финансовых вычислений
n – срок погашения долга (анг. number of
periods) – интервал времени, по истечении которого
сумму долга и проценты нужно вернуть.
Срок измеряется числом расчетных периодов –
обычно равных по длине подинтервалов времени, в
конце которых начисляются проценты.
10.03.2019
19

20.

Ссуда может выдаваться на любой срок, с
любой даты, по любую дату. Первый и
последний дни обычно считаются за один день.
Если начисление процентов будет
производиться m раз в год, а срок погашения
долга – n, то общее количество периодов
начисления за весь срок финансовой операции
составит:
10.03.2019
Основы финансовых вычислений
20

21.

Основы финансовых вычислений
FV – будущая стоимость (англ. future value)
– наращенная сумма или будущая стоимость,
т.е. первоначальная сумма долга с
начисленными на нее процентами к концу
срока ссуды.
10.03.2019
PV – текущая стоимость (англ. present
value) – исходная сумма или оценка
современной величины денежной суммы,
поступление которой ожидается в будущем, в
пересчете на более ранний момент времени.
21

22.

Основы финансовых вычислений
Оценка эффективности финансовых операций
по величине процентных денег на практике
используется редко, т.к. данная величина не
учитывает фактор времени и не может сказать
о реальной доходности организации.
Необходимо иметь возможность сопоставить ее
с темпом обесценивания денег (инфляции) или
результатами другой финансовой операции.
В финансово-экономических расчетах
используются относительные показатели – r –
процентная ставка.
10.03.2019
I – процентные деньги (англ. interest
money), называемые кратко «проценты»,
представляют собой абсолютный доход от
предоставленного долга: I = FV – PV .
22

23.

r – процентная ставка (англ. rate of
interest), характеризующая интенсивность
начисления процентов за единицу времени, отношение суммы процентных денег,
выплачивающихся за определенный период
времени, к величине ссуды.
Данный показатель выражается либо в долях
единицы, либо в процентах:
Основы финансовых вычислений
Коэффициент показывает, во сколько раз
наращенная сумма больше первоначально
вложенной суммы, т.е. является базисным
темпом роста.
10.03.2019
23

24.

Основы финансовых вычислений
называемую учетной ставкой, или
дисконтный множитель (норма банковского
дисконтирования).
Дисконтирование – определение значения
стоимостной величины на некоторый момент
времени при условии, что в будущем она составит
заданную величину.
Дисконтирование позволяет учитывать в
стоимостных расчетах фактор времени.
10.03.2019
Если соотнести сумму процентов (FV - PV) не с
PV, а с будущей стоимостью FV, наращенной по
мере присоединения процентов, то получим
другую меру эффективности – темп снижения
24

25.

Основы финансовых вычислений
Дисконтирование – это приведение денег к
текущему моменту времени, а дисконтный
множитель (d) показывает, какую долю
составляет первоначальная сумма долга в
величине наращенной суммы.
10.03.2019
25

26.

Различие в ставке процентов и учетной ставке
заключается в различии базы для начисления
процентов:
в процентной ставке в качестве базы
берется первоначальная сумма долга:
Основы финансовых вычислений
в учетной ставке за базу принимается
наращенная сумма долга:
10.03.2019
26

27.

При равной величине процентных денег
(I = FV - PV) величина процентной ставки выше
величины учетной ставки.
Основы финансовых вычислений
В случае, когда процентная и учетная ставка
равны по своей величине, - приведенная
величина FV по процентной ставке меньше ее
значения по учетной ставке.
10.03.2019
27

28.

10.03.2019
Процентная ставка может быть легко
вычислена по известной величине учетной
ставки:
Основы финансовых вычислений
28

29. Пример 1.

ПРИМЕР 1.
Вы заняли сегодня 100 руб., дав обязательство
вернуть к указанной дате 120 руб.
Оценим доходность этой сделки для кредитора
величинами процентной (r) и учетной (d)
ставок, приняв весь период между двумя
моментами времени за полный срок договора,
приняв его за единицу времени n=1.
Основы финансовых вычислений
PV=100 руб., FV=120 руб.
I = (FV – PV)=120 – 100 = 20 руб.
r = 20/100=20%
d = 20/120 = 16,67%
10.03.2019
РЕШЕНИЕ
29

30. Пример 2.

ПРИМЕР 2.
РЕШЕНИЕ
Из формул начисления процентов по
процентной и учетной ставке:
FV проц = PV*(1+r)
FV учетн = PV/(1-d)
Откуда при r = d = 0,2
FV проц = 100 руб.*(1+0,2) = 120 руб.
FV учетн = 100 руб./(1-0,2) = 125 руб.
Основы финансовых вычислений
Вы обратились к кредитору с просьбой о займе
100 руб. (PV) на срок 1 год (n = 1). Какую
сумму сможет получить кредитор по окончании
срока займа при процентной и учетной ставке
= 20%?
10.03.2019
30

31. 2. Простые проценты

2. ПРОСТЫЕ ПРОЦЕНТЫ
Математическая модель задачи представлена
в виде модели простых процентов.
В данной модели накопление наращенной
суммы FV (общей суммы долга) происходит за
счет периодического (например, ежегодного)
начисления процентных денег (I).
Основы финансовых вычислений
Пусть кредитор и заемщик договариваются о
величине кредита PV (первоначальная
денежная сумма), размере годовой процентной
ставки (r), сроке кредита (T) и длительности
периода начисления процентов (n).
10.03.2019
31

32.

к концу второго года:
к концу n-го года:
Основы финансовых вычислений
Таким образом, наращенная сумма равна:
к концу первого года:
10.03.2019
Процентные деньги – это разность между
первоначальной денежной суммой PV и
наращенной денежной суммой FV:
I = FV – PV.
32

33.

При использовании простых ставок процентов
проценты (процентные деньги) определяются
исходя из первоначальной суммы долга. Схема
простых процентов предполагает неизменность
базы, с которой происходит начисление
процентов.
Основы финансовых вычислений
которая представляет собой арифметическую
прогрессию с первым членом PV и разностью
прогрессии I = FV – PV.
10.03.2019
Таким образом, накопление суммы происходит
по схеме простых процентов и образует
возрастающую числовую последовательность:
33

34.

10.03.2019
Основы финансовых вычислений
Рис. 4. Наращивание первоначальной суммы
по схеме простых процентов.
34

35.

общем случае, модель накопления капитала
по схеме простых процентов имеет вид:
Учитывая,
что I = PV*r, модель простых
процентов можно записать в виде:
где
kн коэффициент наращения.
Основы финансовых вычислений
В
10.03.2019
Таким образом, размер ожидаемой наращенной
суммы долга (дохода) зависит от трех факторов:
величины инвестированной суммы;
уровня процентной ставки;
срока финансовой операции.
35

36. 2.1. Временная база финансовой операции

2.1. ВРЕМЕННАЯ БАЗА ФИНАНСОВОЙ ОПЕРАЦИИ
Основы финансовых вычислений
В банковской практике разных стран расчетное
число дней в году при начислении процентов
определяется по-разному.
Срок ссуды n может быть как целым, так и дробным
положительным числом.
Если срок ссуды менее года, происходит
модификация формулы:
1) Если срок ссуды выражен в месяцах (M), то
величина n выражается в виде дроби:
2) Если время выражено в днях (t), то величина n
выражается в виде дроби:
где t – число дней ссуды, т.е. продолжительность
срока, на который выдана ссуда;
T – расчетное число дней в голу (временная база).
10.03.2019
36

37.

Число дней ссуды (t) также можно определить поразному:
1) условно, исходя из того, что продолжительность
любого целого месяца 30 дней, оставшиеся дни считают
точно. В результате получают т.н. приближенное
число дней ссуды.
2) используя прямой счет или специальные таблицы
порядковых номеров дней года, рассчитывают
фактическое число дней между датами, - в результате
получают точное число дней ссуды.
Основы финансовых вычислений
10.03.2019
Временную базу (T) можно представить по-разному:
1) условно состоящую из 360 дней – т.н.
обыкновенный или коммерческий процент.
2) действительное число дней в году (365 или 366 дней)
– т.н. точный процент.
37

38.

Таким образом, если время финансовой
операции выражено в днях, то расчет простых
процентов производится одним из трех
способов:
1) Обыкновенные проценты с
приближенным числом дней ссуды
(германская практика расчета):
продолжительность года условно принимается
360 дней, а продолжительность месяца – 30
дней.
Используется в Германии, Дании, Швеции.
10.03.2019
Основы финансовых вычислений
38

39.

2) Обыкновенные проценты с точным
числом дней ссуды (французская практика
расчета): продолжительность года – 360 дней, а
продолжительность ссуды рассчитывают точно
по календарю.
Используется во Франции, Бельгии, Испании,
Швейцарии.
10.03.2019
Основы финансовых вычислений
3) Точные проценты с точным числом
дней ссуды (английская практика расчета):
продолжительность года и продолжительность
ссуды берутся точно по календарю.
Используется в Португалии, Англии, США.
39

40. 2.2. Переменная ставка

2.2. ПЕРЕМЕННАЯ СТАВКА
Основы финансовых вычислений
Ставка процентов не является застывшей
величиной, в финансовых операциях
используются и дискретно изменяющиеся во
времени процентные ставки (например,
наличие инфляции вынуждает собственника
периодически варьировать процентной
ставкой).
10.03.2019
40

41.

Основы финансовых вычислений
где коэффициент наращения (kн) вычисляется
по формуле:
10.03.2019
Если на последовательных интервалах
начисления процентов n1, n2, n3, … nm
устанавливаются разные процентные ставки
r1, r2, r3, …, rm, то наращенная сумма
вычисляется по формуле:
41

42. Пример 1.

ПРИМЕР 1.
Наращенная сумма: FV = PV(1+n*r) = 2000(1+1*0,1) = 2200 руб.
или
FV = PV*kн = 2000*1,1 = 2200 руб.
Сумма начисленных процентов:
I = PV*n*r = 2000*1*0,1 = 200 руб.
или
I = FV – PV = 2200 – 2000 = 200 руб.
Таким образом, через год нужно вернуть 2200 руб.: 2000 руб. –
долг и 200 руб. – «цена долга» (процентные деньги).
Основы финансовых вычислений
РЕШЕНИЕ:
10.03.2019
Сумма в размере 2000 руб. дана в долг на 1 год по
схеме простого процента под 10% годовых.
Определить проценты и сумму, подлежащую
возврату.
42

43. Пример 2.

ПРИМЕР 2.
Ссуда выдана под 10% годовых сроком:
1) на 5 месяцев;
2) на 3 месяца.
Определить процентную ставку за срок ссуды.
Основы финансовых вычислений
1) n = 5/12 = 0,42
r 5 мес = 0,1*5/12 = 0,0417;
2) n = 3/12 = 0,25;
r 3 мес = 0,1*3/12 = 0,025.
10.03.2019
РЕШЕНИЕ:
43

44. Пример 3.

ПРИМЕР 3.
РЕШЕНИЕ:
Наращенная сумма:
FV = PV(1+n*r) = 50000*(1+0,5*0,14) = 53500
руб.
Сумма начисленных процентов:
I = FV – PV = 53500 – 50000 = 3500 руб.
Основы финансовых вычислений
Ссуда в размере 50000 руб. выдана на полгода
по простой процентной ставке 14% годовых.
Определить наращенную сумму и сумму
начисленных процентов.
10.03.2019
44

45. Пример 4.

ПРИМЕР 4.
PV = 110000/(1+0,1*2/12) = 108196,7 руб.
Основы финансовых вычислений
РЕШЕНИЕ:
10.03.2019
Определить сумму вклада, который надо положить
в банк сроком на 2 месяца под 10% годовых, чтобы
к концу срока получить 110000 руб.
45

46. Пример 5.

ПРИМЕР 5.
Основы финансовых вычислений
Клиент внес вклад в банк в сумме 1 тыс. руб.
сроком на 1 год. Процентная ставка до
середины второго квартала составляла 30%
годовых, далее до конца третьего квартала –
25%, а с начала четвертого квартала – снова
30%. Какую сумму получил клиент в конце
года?
10.03.2019
46

47. Решение:

РЕШЕНИЕ:
Основы финансовых вычислений
10.03.2019
1) с начала года до середины второго квартала (n1) равен
4,5 месяца или 4,5/12 = 0,375 года.
2) от середины второго квартала до конца третьего (n2)
равен 4,5 месяца или 4,5/12 = 0,375 года.
3) с конца третьего квартала и до конца четвертого (n3)
равен 3 месяца или 3/12 = 0,25 года.
Коэффициент наращения:
1) за период до середины второго квартала:
k1 = 0,3*0,375 = 0,113
2) от середины второго квартала до начала четвертого
квартала:
k2 = 0,25*0,375 = 0,094
3) за четвертый квартал:
k3 = 0,3*0,25 = 0,075
4) за год
kгод = k1 + k2 + k3 = 0,113 + 0,094 + 0,075 = 0,281.
В результате в конце года клиент получит сумму:
FV = PV*(1+ kгод) = 1281,25 руб.
47

48. 2.3. Определение срока ссуды и величины процентной ставки

2.3. ОПРЕДЕЛЕНИЕ СРОКА ССУДЫ И
ВЕЛИЧИНЫ ПРОЦЕНТНОЙ СТАВКИ
10.03.2019
Основы финансовых вычислений
Иногда в финансово-экономических расчетах
срок финансовой операции в условиях
конкретной финансовой сделки не может быть
оговорен заранее.
Аналогично возникает ситуация и с
неопределенностью процентной ставки
(например, при заключении сделки нас
интересует только величина вложения PV и
полученная сумма FV).
48

49.

Срок финансовой операции может быть
определен так
1) при определении срока в годах:
Процентная ставка может быть определена как
Основы финансовых вычислений
2) при определении срока в днях:
10.03.2019
49

50. Пример 1.

ПРИМЕР 1.
РЕШЕНИЕ:
n = (FV – PV)/(PV*r) = (2000 – 1000)/(1000*0,08)
= 12,5 года.
Основы финансовых вычислений
За какое время может быть накоплена сумма в
2000 долларов, если сегодня мы можем
оформить депозитный вклад 1000 долларов
под 8% годовых?
10.03.2019
50

51. Пример 2.

ПРИМЕР 2.
РЕШЕНИЕ:
t = [(FV – PV)/(PV*r)]*T = ((1100 –
1000)/(1000*0,08))*360 = 450 дней
Основы финансовых вычислений
На сколько дней можно дать в долг 1000
долларов, исходя из 8% годовых, если
возвращенная сумма должна составлять 1100
долларов?
10.03.2019
51

52. Пример 3.

ПРИМЕР 3.
Рассчитаем годовую процентную ставку,
используя формулу «обыкновенного процента» ,
т.к. нет ссылки на точный процент:
r = [(FV – PV)/(PV*t)]*T = [(12001150)/(1150*120)]*360 = 0,13.
Основы финансовых вычислений
РЕШЕНИЕ:
10.03.2019
В контракте предусматривается погашение
обязательств через 120 дней в сумме 1200
долларов, при первоначальной сумме долга
1150 долларов. Определить доходность
операции для кредитора в виде процентной
ставки.
52

53. Пример 4.

ПРИМЕР 4.
Банк выдал ссуду в размере 100000 рублей
сроком
1) на 5 месяцев;
2) на 3 месяца.
Какими должны быть процентные ставки с
тем, чтобы доход банка (не зависимо от срока
ссуды) составил 120000 рублей?
Основы финансовых вычислений
1) Находим r = [(FV – PV)/(PV*t)]*T = [(120000100000)/(100000*5)] *12 = 0,48
2) r = [(FV – PV)/(PV*t)]*T = [(120000100000)/(100000*3)] *12 = 0,8
10.03.2019
РЕШЕНИЕ:
53