Похожие презентации:
Основы финансовой математики
1.
ФГБОУ ВПО ««Магнитогорский государственный техническийуниверситет им Г.И. Носова»
Институт энергетики и автоматизированных систем
Кафедра бизнес-информатики и информационных технологий
Лекции по курсу:
«Основы финансовой
математики»
Чусавитина Галина Николаевна
Магнитогорск
МЭ1
2.
Лекция 4. Дисконтирование по сложной ставкеПлан лекции
4.1 Дисконтирование по сложной процентной
ставке r.
4.2 Дисконтирование по сложной учетной
ставке d.
4.3 Определение срока платежа и ставок.
4.4 Непрерывные проценты.
4.5 Финансовые функции Ехсеl.
3.
4.1 Дисконтирование по сложной процентнойставке r
Оценивая целесообразность финансовых вложений в тот или иной вид
бизнеса, исходят из того, является ли это вложение более прибыльным (при
допустимом уровне риска), чем вложения в государственные ценные бумаги, или
нет. Используя несложные методы, пытаются проанализировать будущие доходы
при минимальном, «безопасном» уровне доходности.
Основная идея этих методов заключается в оценке будущих поступлений FV
(например, в виде прибыли, процентов, дивидендов) с позиции текущего
момента. При этом, сделав финансовые вложения, инвестор обычно
руководствуется тремя посылками:
1)
происходит перманентное обесценение денег (инфляция);
2)
темп изменения цен на сырье, материалы и основные средства,
используемые предприятием, может существенно отличаться от темпа инфляции;
3)
желательно периодическое начисление (или поступление) дохода, причем в
размере, не ниже определенного минимума.
Базируясь на этих посылках, инвестор должен оценить, какими будут его
доходы в будущем, какую максимально возможную сумму допустимо
вложить в данное дело исходя из прогнозируемой его рентабельности.
4.
Формула дисконтирования по сложнойпроцентной ставке r
Формула наращения сложными процентами :
FV PV 1 r
n
(4.1)
Формула дисконтирования по сложной
процентной ставке:
FV
PV
(1 r ) n
1
(1 r) n
(4.2)
Величину
(4.3)
называют множитель дисконтирования, или дисконтный
множитель
Величину PV, полученную дисконтированием FV, называют
современной, текущей, стоимостью, или современной
величиной FV.
5.
Экономический смысл такого представлениязаключается в следующем:
прогнозируемая величина денежных поступлений через
n лет (FVn) с позиции текущего момента будет меньше
и равна РV (поскольку знаменатель дроби больше
единицы). Это означает также, что для инвестора
сумма РV в данный момент времени и сумма FVn
через n лет одинаковы по своей ценности.
6.
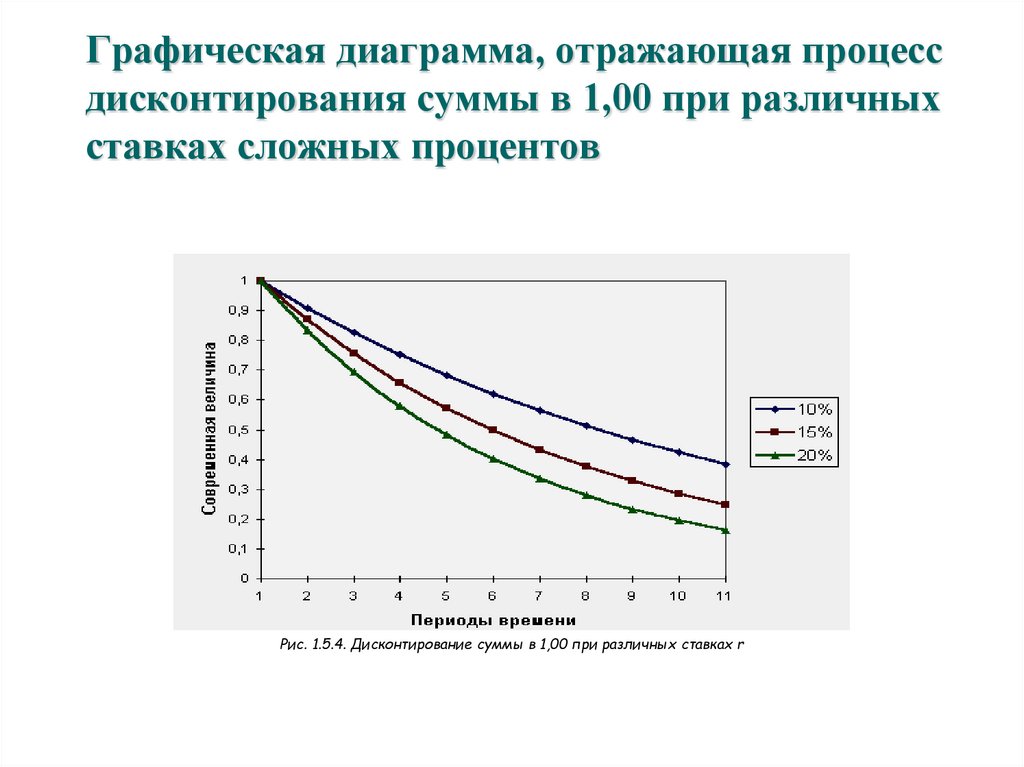
Графическая диаграмма, отражающая процессдисконтирования суммы в 1,00 при различных
ставках сложных процентов
Рис. 1.5.4. Дисконтирование суммы в 1,00 при различных ставках r
7.
Дисконт:FV
n
(4.4)
D FV PV FV
FV
(
1
(
1
r
)
)
(1 r ) n
Формула дисконтирования при m-кратном
начислении процентов в год:
PV
FV
r mn
(1 )
m
.
(4.5)
8.
Пример 1.4.1 Из какого капитала можно получить 4 тыс. руб. через 5 летнаращением сложными процентами 12 % годовых, если наращение
осуществляется а) ежегодно, б) ежеквартально.
Решение:
В данном примере n = 5, FV5 = 4, r = 0,12.
а) При ежегодном наращении пользуемся формулой :
4
PV
2,2696 тыс. руб.
5
(1 0,12)
D = 4 – 2,2696 = 1,7304 тыс.руб.
б) При ежеквартальном начислении воспользуемся формулой:
FV
4
PV
2,2148 тыс. руб.
r m n (1 0,03) 4 5
(1 )
m
D = 4 – 2,2148 = 1,7852 тыс.руб.
9.
4.2 Дисконтирование (учет) по сложной учетнойставке (банковское дисконтирование)
PV FV (1 d )
n
(4.6)
где (1-d)n - дисконтный множитель.
(4.7)
Дисконтирование по сложной учетной ставке,
осуществляемого несколько раз в год:
d
PV FV 1
m
mn
(4.8)
где n – число периодов (лет), m – количество
осуществлений операции дисконтирования за
период (в год).
10.
Пример 2.4.2 Долговое обязательство на сумму 5 млн руб., срокоплаты которого наступает через 5 лет, продано с дисконтом по
сложной учетной ставке 15% годовых. Каков размер полученной за
долг суммы и величина дисконта (в тыс. руб.)? Имеем
PV = 5000(1 – 0,15)5 = 2218,5; D = 5000-2218,5 – 2781,5.
Если применить простую учетную ставку того же размера, то
PV = 5000(1 – 5х0,15) = 1250; D = 5000-1250 = 3750.
Как следует из приведенного примера, дисконтирование по сложной
учетной ставке выгоднее для должника, чем по простой учетной ставке.
Сказанное становится понятным при сравнении формул для
дисконтных множителей:
1 nd1
и
(1 d 2 ) n
,
где d1 и d2 – простая и сложная учетные ставки соответственно.
11.
Пример 3.4.2 Найдите величину дисконта, если долговоеобязательство на выплату 40 тыс. руб. учтено за 3 года до срока
погашения по сложной учетной ставке: а) 20% годовых; б) 25%
годовых.
Решение: а) Полагая n = 3, F3=40 тыс. руб., d = 0,2, получим:
PV 40(1 0,2)3 20,48 тыс. руб.
Поэтому дисконт составит:
Da ) 40 20,48 19,52
тыс. руб.
б) Так как в этом случае d = 0,25, то
PV 40(1 0,25) 16,875
тыс. руб.
Dб ) 40 16,875 23,125
тыс. руб.
3
12.
Расчет современнойнецелого числа лет.
Первый способ:
стоимости
в
случае
mn
d
PV FV 1 ,
m
(4.9)
Второй способ:
Формула дисконтирования по смешанной схеме:
PV FV (1 d ) w (1 fd ),
(4.10)
где w – целое число периодов дисконтирования по
сложной учетной ставке, f – дробная часть периода, n =
w+f.
13.
Пример 4.4.2 Вексель на сумму 70 тыс. руб. со сроком погашения через 4года учтен за 32 месяца по сложной учетной ставке 24% годовых.
Определите суммы, которые получит предъявитель векселя при различных
способах учета векселя.
Решение. При применении только сложной учетной ставки, так как
дисконтирование производится один раз в год, то n = 32/12 = 8/3. Далее
Fn =70 тыс. руб., d = 0,24, поэтому:
8
3
PV 70(1 0,24) 33,672
тыс. руб.
Если же использовать при учете смешанную схему, то при w = 2, f =
2/3 получим:
2
PV 70(1 0,24) (1 0,24) 33,963
3
2
тыс. руб.
14.
Номинальная и эффективная учетныеставки
Дисконтирование может производиться не один, а m раз в году,
т.е. каждый раз учет производится по ставке f/m. В этом случае:
где
f
f mn
PV FV (1 ) ,
m
(4.11)
– номинальная годовая учетная ставка.
Эффективная учетная ставка (d) характеризует степень дисконтирования за
год. Определим ее на основе равенства дисконтных множителей:
откуда
(1 d ) n (1
В свою очередь
d 1 (1
f mn
) ,
m
f m
) ,
m
(4.12)
Эффективная учетная ставка во всех случаях, когда m > 1, меньше
номинальной.
(4.13)
f m(1 m 1 d ),
15.
Пример 5.4.2 По данным примера 2 определим сумму,полученную при поквартальном учете по номинальной
учетной ставке 15%, и эффективную учетную ставку.
Имеем f = 0,15; m = 4; mn = 20;
0,15 20
P 5000(1
) 2328,0
4
тыс. руб
Эффективная учетная ставка составит
0,15 4
d 1 (1
) 0,14177,
4
или 14,177%
16.
4.3 Определение срока платежа процентной иучетной ставок
Формула для определения срока ссуды (при
использовании сложной учетной ставки):
PV
ln
FVn
n
.
(m)
d
m ln 1
m
(4.14)
17.
4.4 Непрерывные процентыПо мере увеличения числа начислений процентов в течение
года (m) промежуток времени между двумя смежными
начислениями уменьшается - при m = 1 этот промежуток
равен 1 году, а при m = 12 - только 1 месяцу. Теоретически
можно представить ситуацию, когда начисление сложных
процентов производится настолько часто, что общее его
число в году стремится к бесконечности, тогда величина
промежутка между отдельными начислениями будет
приближаться к нулю, то есть начисление станет
практически непрерывным. Такая на первый взгляд
гипотетическая ситуация имеет важное значение для
финансов и при построении сложных аналитических
моделей (например при разработке масштабных
инвестиционных проектов) часто применяют
непрерывные проценты.
18.
Природа и происхождение сложного процентаПочему же в расчетах применяются не только простые, но и сложные
проценты? Это отражение объективной реальности. Поясним, как люди пришли к
сложным процентам на примере.
Предположим, что два клиента поместили каждый по 1000 руб. в банк под
200% годовых на бессрочный депозит. Депозитов с такими условиями нет и не
было. Сейчас вы разберетесь почему. «Ленивый» клиент добросовестно
продержал деньги целый год на счете в банке и в результате получил 3000 руб.
«Активный» клиент пришел в банк через полгода, взял причитающиеся к этому
моменту 2000 руб. со счета и тут же положил их снова. За вторую половину года
эта сумма удвоилась и в итоге он через год имеет уже 4000 рублей. Заметьте, что
банкиру это невыгодно не только потому, что приходится платить больше, но и
потому что нужно изымать капитал из обращения. К тому же «сверхактивный»
клиент догадается приходить и раз в квартал:
Формулу напишите самостоятельно = 5062,5 руб.
и даже чаще, хоть каждый день:
Формулу напишите самостоятельно = 7388,6 руб.
Ежедневное или чаще начисление процентов называется непрерывным и
приближенно, с хорошей степенью точности, вычисляется с помощью числа e =
2,7182818. (константа Л.Эйлера e=2,718281828459045).
19.
Непрерывная процентная ставка (очевидно, что при непрерывномначислении речь может идти только о сложных процентах)
обозначается буквой (читается «дельта»), часто этот показатель
называют «сила роста». Формула наращения по непрерывной
процентной ставке имеет вид:
FV PV e n ,
где
(4.15)
e - основание натурального логарифма ( 2,71828...),
e n - множитель наращения непрерывных процентов.
Таким образом, в нашем примере при непрерывном начислении процентов
доход на вложенный капитал составит почти 738% - 100% = 638% годовых.
20.
Пример 6.4.4 Чему будет равна через 3 года сумма 250 тыс. рублей, если сегодняположить ее на банковский депозит под 15% годовых, начисляемых непрерывно?
Решение. По формуле непрерывных процентов получаем:
FV PV e n 250 e0,15 3 392,07805
тыс. рублей
Для непрерывных процентов не существует различий между процентной и
учетной ставками – сила роста является универсальным показателем. Однако
наряду с постоянной силой роста, может использоваться переменная процентная
ставка, величина которой меняется по заданному закону (математической
функции). В этом случае можно строить очень мощные имитационные модели,
однако математический аппарат расчета таких моделей достаточно сложен и не
рассматривается в настоящем пособии, так же как и начисление процентов по
переменной непрерывной процентной ставке.
Непрерывное дисконтирование с использованием постоянной силы роста
выполняется по формуле:
PV FV e
где
1 / e n
n
FV
n ,
e
- дисконтный множитель по силе роста.
(4.16)
21.
Пример 7.4.4 В результате осуществления инвестиционного проектапланируется получить через 2 года доход в размере 15 млн. рублей. Чему будет
равна приведенная стоимость этих денег в сегодняшних условиях, если сила
роста составляет 22% годовых?
Решение. По формуле дисконтирования по непрерывным процентам получаем:
FV
15
PV n 0, 22 2 9,66054632 млн. рублей.
e
e
22.
Эквивалентность процентных ставокОдин и тот же финансовый результат можно получить различными способами, используя
различные ставки, методы наращения и дисконтирования.
Две ставки называются эквивалентными, если при замене одной ставки на другую финансовые
отношения сторон не меняются. Таким образом, участникам финансового соглашения безразлично,
какая ставка будет фигурировать в контракте.
При выводе равенств, связывающих эквивалентные ставки, используется следующая идея: если
из первоначального капитала наращением за данное время необходимо получить некоторую сумму,
то будут эквивалентными все ставки, обеспечивающие один и тот же множитель наращения.
Поэтому приравнивая друг к другу множители наращения, получим соотношения между
эквивалентными ставками. Точно так же при переходе от будущей стоимости к приведенной
стоимости с помощью дисконтирования приравниваются множители дисконтирования.
Эквивалентные ставки, подобно эффективным ставкам, позволяют сравнивать между собой
финансовые контракты, условия которых различны.
Формулы, связывающие эквивалентные простые и сложные ставки, зависят от
продолжительности периода начисления. Формулы, связывающие эквивалентные сложные ставки,
не зависят от продолжительности периода начисления.
Переход от дискретных ставок к соответствующим эквивалентным непрерывным ставкам
позволяет упростить анализ многих сложных финансовых задач. Осуществив необходимые
математические выкладки, полученные результаты можно представить опять в любых удобных
эквивалентных дискретных ставках, являющихся более привычными.
Проблему эквивалентности ставок можно рассматривать и с более общих позиций, например
эквивалентность одной ставки нескольким ставкам или эквивалентность двух наборов ставок и т.п.
23.
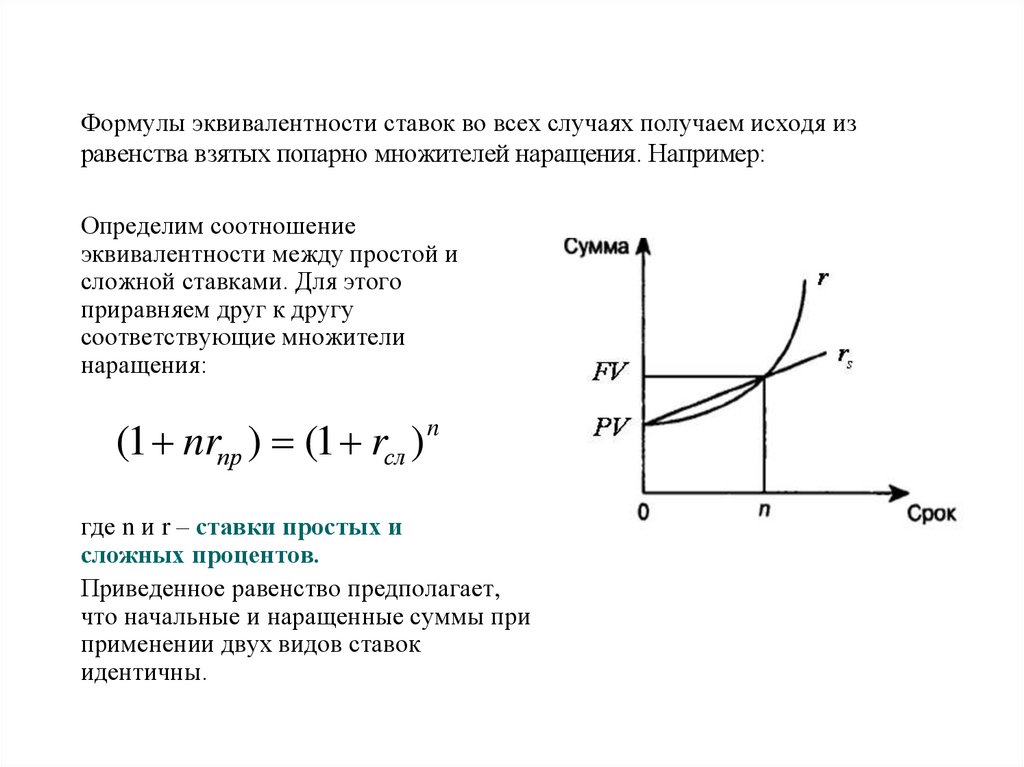
Формулы эквивалентности ставок во всех случаях получаем исходя изравенства взятых попарно множителей наращения. Например:
Определим соотношение
эквивалентности между простой и
сложной ставками. Для этого
приравняем друг к другу
соответствующие множители
наращения:
(1 nrпр ) (1 rсл ) n
где n и r – ставки простых и
сложных процентов.
Приведенное равенство предполагает,
что начальные и наращенные суммы при
применении двух видов ставок
идентичны.
24.
Решение приведенного выше равенства дает следующиесоотношения эквивалентности:
(1 r )
rs
1,
n
r
n
1 nr 1.
Аналогичным образом определим и другие, приведенные
ниже, соотношения эквивалентности ставок.
25.
Эквивалентность простых процентных ставокПри выводе искомых соотношений между ставкой процента и
учетной ставкой следует иметь в виду, что при применении этих
ставок используется временная база Т=360 или Т=365 дней. Если
временные базы одинаковы, то из равенства соответствующих
множителей наращения следует:
ds
rs
1 nd s
(4.17)
r
1 rs
(4.18)
ds
где n – срок в годах, rs –ставка простых процентов,
ds – простая учетная ставка.
26.
Пример 8.4.4 Вексель учтен за год до даты его погашенияпо учетной ставке 15%. Какова доходность учетной
операции в виде процентной ставки? По формуле находим
0,15
rs
0,17647, или17,647%
1 0,15
Иначе говоря, операция учета по учетной ставке 15% за год
дает тот же доход, что и наращение по ставке 17,647%.
27.
Если временные базы разные, тогда, подставив в () n=t/T (t-срок наращенияпроцентов в днях, T-временная база), получим варианты соотношений
эквивалентности:
А) временные базы одинаковы и равны 360 дням:
360
rs
,
360 td s
360rs
ds
;
360 rs
(4.19)
(4.20)
Б) если при начислении процентов принята база К=365, а для учетной ставки
К=360, то
365d s
rs
,
360 td s
(4.21)
360rs
ds
.
365 trs
(4.22)
28.
Пример 9.4.4 Необходимо найти величину учетной ставки,эквивалентной годовой процентной ставке 40% (К=365)
при условии, что срок учета равен 255 дням.
Решение. Находим по формуле (4.22):
360 0,4
d
0,30835, или30,835%
365 255 0,4
29.
Эквивалентность простых и сложных ставок:Рассмотрим соотношения эквивалентности простых
ставок r и d, с одной стороны, и сложных ставок r (m) и d (m), с
другой. Сложную учетную ставку здесь не будем принимать
во внимание. Попарно приравняв друг к другу
соответствующие множители наращения, получим набор
искомых соотношений.
r
1
m
r
n
(m)
r
( m)
mn
1
, (4.23)
m( 1 nr 1).
mn
(4.24)
30.
d1 1
m
d
n
(m)
mn
,
d ( m) m(1 mn 1 nd ),
d (m)
1
m
r
n
d
( m)
(4.25)
(4.26)
mn
1
,
1
m 1 mn
,
1 nr
r
1 1
m
d
n
(m)
(4.27)
(4.28)
mn
,
(4.29)
31.
1r ( m ) m mn
1 ,
1 nd
(4.30)
где r, d - простые ставки,
r (m) и d (m) - сложные ставки.
1
m
r
r ( m ) m[ 1
1],
l
(l )
1
m
d
d ( m ) m[1 1
],
l
(l )
d
m[ 1
l
(l )
r
(m)
1
m
1],
1
m
r
d ( m ) m[1 1
].
l
(l )
(4.31)
(4.32)
(4.33)
(4.34)
32.
Пример 10.4.4 Какой сложной годовой ставкой можнозаменить в контракте простую ставку 18% (К-365), не
изменяя финансовых последствий? Срок операции 580
дней.
Решение. По формуле () находим эквивалентную сложную
ставку:
r
580
365
580
1
0,18 1 0,17153, или17,153%
365
33.
Пример 11.4.4 При разработке условий контракта стороныдоговорились о том, что доходность кредита должна
составлять 24% годовых. Каков должен быть размер
номинальной ставки при начислении процентов
ежемесячно, поквартально?
12
1,24 1) 0,21705;
4
1,24 1) 0,22100.
r 12(
m
r 4(
m
34.
Эквивалентность сложных дискретных инепрерывных ставок.
Теоретически можно найти соотношение эквивалентности между силой роста
и любой дискретной процентной ставкой. Однако в этом, вероятно, нет
необходимости. Ограничимся несколькими такими соотношениями,
необходимость в которых может возникнуть в практических расчетах:
Эквивалентность силы роста и простых ставок:
e n 1
r
,
n
(4.35)
ln(1 nr)
,
n
(4.36)
1 e n
d
,
n
(4.37)
ln(1 nd )
.
n
(4.38)
35.
r (m)(4.39)
m ln(1
),
m
Эквивалентность силы роста и сложных ставок:
r ( m ) m(e m 1),
(4.40)
d (m)
m ln(1
),
m
(4.41)
d ( m ) m(1 e m ).
(4.42)
36.
Пример 12.4.4 Какая непрерывная ставка заменитпоквартальное начисление процентов по номинальной
ставке 20%? Находим
=
4 ln( 1 0,2) 0,19516, или19,516%
Формулы эквивалентности дискретных и непрерывных
ставок позволяют расширить применение непрерывных
процентов. Как уже говорилось выше, непрерывные
проценты во многих сложных расчетах позволяют
существенно упростить выкладки. Вместе с тем такие ставки
непривычны для практика, поэтому испоьзуя формулы
эквивалентности, нетрудно представить полученные
результаты в виде общепринятых характеристик.
37.
Пример 13.4.4 Господин N собирается поместить на некоторый сроксвободные денежные средства либо под сложную процентную ставку 30%
годовых с ежеквартальным начислением процентов, либо под простую
процентную ставку 48% годовых. Выясните, как выгоднее поступить при
сроке 3 года.
Решение. Чтобы сделать правильный выбор, необходимо найти для
данной сложной процентной ставки 30% эквивалентную простую процентную
ставку и сравнить ее с предлагаемой простой процентной ставкой 48%.
Используем формулу (81) при n = 3, m = 4 , r(4) = 0,3:
0,3
1
4
r
3
4 3
1
0,4606.
Так как r = 46,06% меньше 48%, то выгоднее на три года поместить капитал под
простую процентную ставку 48%.
38.
4.5 Финансовые функции ЕхсеlДля вычислений, связанных с денежными потоками, в Ехсеl
используется общая формула:
1 r 1
PV 1 r FV C
1 r type 0 (4.43)
n
n
r
где C – фиксированная (неизменная) периодическая
сумма платежа;
n – общее число периодов выплат;
r– процентная ставка за один период;
type – число 0 или 1, обозначающее, когда производится
выплата (1 – в начале периода, 0 в конце периода);
PV – текущая стоимость;
FV– будущая стоимость.
39.
В случае r = 0 (например, беспроцентной ссуды) применяется формула:PV FV C n 0
(4.44)
Финансовые функции электронных таблиц Ехсеl для расчета
операций по вкладам (займам) и кредитам имеют одинаковый набор
аргументов (параметров):
Ставка — процентная ставка за период. Например, если получена
ссуда на автомобиль под 10 процентов годовых и делаются
ежемесячные выплаты, то процентная ставка за месяц составит 10%/12
или 0,83%. В качестве значения аргумента ставка нужно ввести в
формулу 10%/12 или 0,83% или 0,0083.
Кпер — общее число периодов платежей. Например, если получена
ссуда на 4 года под автомобиль и делаются ежемесячные платежи, то
ссуда имеет 4*12 (или 48) периодов. В качестве значения аргумента
кпер в формулу нужно ввести число 48.
40.
Плт — выплата, производимая в каждый период и неменяющаяся за все время выплаты ренты.
Бс — требуемое значение будущей стоимости или остатка
средств после последней выплаты. Если аргумент опущен,
он полагается равным 0 (будущая стоимость займа,
например, равна 0).
Пс — это приведенная к текущему моменту стоимость
или общая сумма, которая на текущий момент равноценна
ряду будущих платежей. Если аргумент нз опущен, то он
полагается равным 0. В этом случае должно быть указано
значение аргумента плт.
Тип — число 0 или 1, обозначающее, когда должна
производиться выплата (.0 или опущен - в конце периода,
1 - начале периода).
41.
Функция БС (ставка; кпер; плт ;пс ;тип) возвращает будущуюстоимость инвестиции на основе периодических постоянных (равных
по величине сумм) платежей и постоянной процентной ставки.
Пример 14.4.5 Рассчитаем, какая сумма окажется на счете, если 10
тыс. руб. положены в «КУБ» на «Вклад до востребования», с
ежемесячным начислением сложных процентов 6% годовых на 3
года.
Решение.
В данной задаче при ежемесячном начислении процентов общее
число периодов начисления равно 3 12 (аргумент Кпер), а процент за
период начисления равен 6%/12 (аргумент Ставка). По условию
Плт=- 10000. Это отрицательное число, означающее вложение денег.
Используя функцию БС, получим:
БС(6%/12; 3*12;; -10000) = 11 966,81р.
42.
Домашняя контрольная работа № 3Сложная процентная ставка;
Сложная учетная ставка;
Непрерывная ставка
Эквивалентность ставок
43.
Вопросы1. Дисконтирование по сложной процентной ставке r.
2. Дисконтирование по сложной учетной ставке d.
3. Определение срока платежа и
4. Непрерывные проценты.
5. Эквивалентность ставок.
6. Финансовые функции Ехсеl.
ставок.



























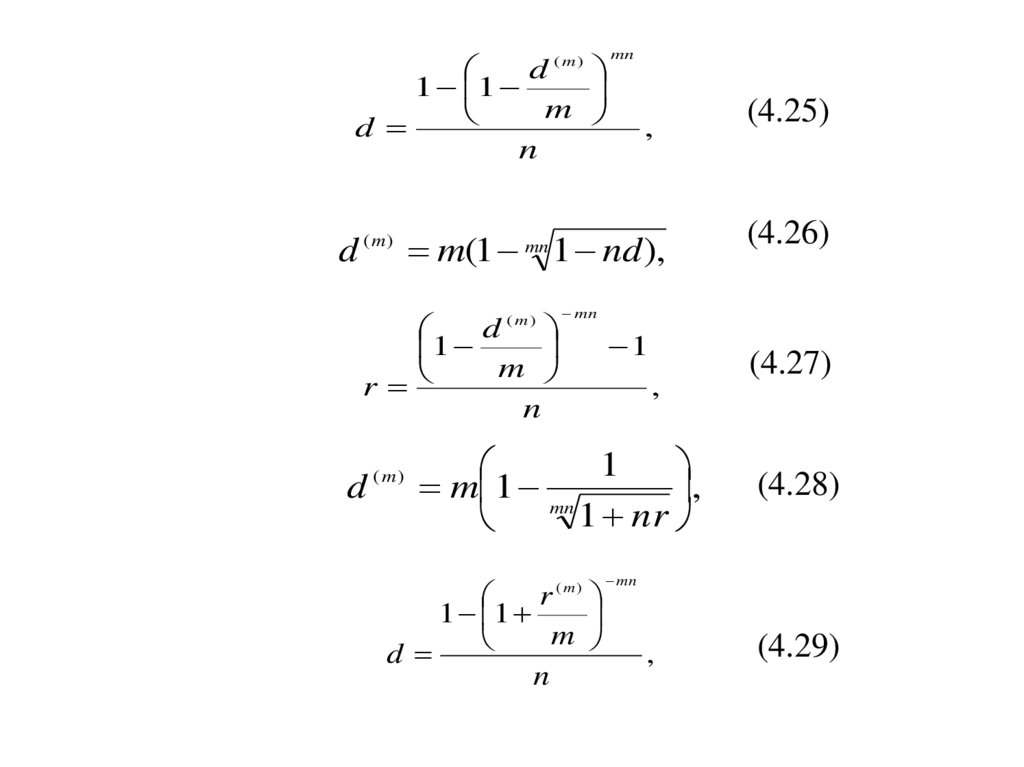














 Математика
Математика Финансы
Финансы








