Похожие презентации:
Моделирование транспортных процессов (Лекция 1-2)
1. Дисциплина: «Моделирование транспортных процессов»
Преподаватель:Мокляк Денис Сергеевич
2. Тема лекции № 1.1
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕТРАНСПОРТНЫХ ПРОЦЕССОВ И
ПРИНЦИПЫ ИХ ПОСТРОЕНИЯ.
3. Цель лекции – изучить основные виды моделей и способы их построения
План лекции.1. Понятие математических моделей
и их классификация.
2. Детерминированные модели.
3. Вероятностные модели.
4. Агрегатные модели.
4. 1. Понятие математических моделей и их классификация.
Математическая модель — приближенноеописание объекта моделирования,
выраженное с помощью математической
символики.
Математическое моделирование – процесс
определения соответствия данной реальной
системы некоторой математической модели
и исследование этой модели, позволяющее
получить характеристики реальной системы.
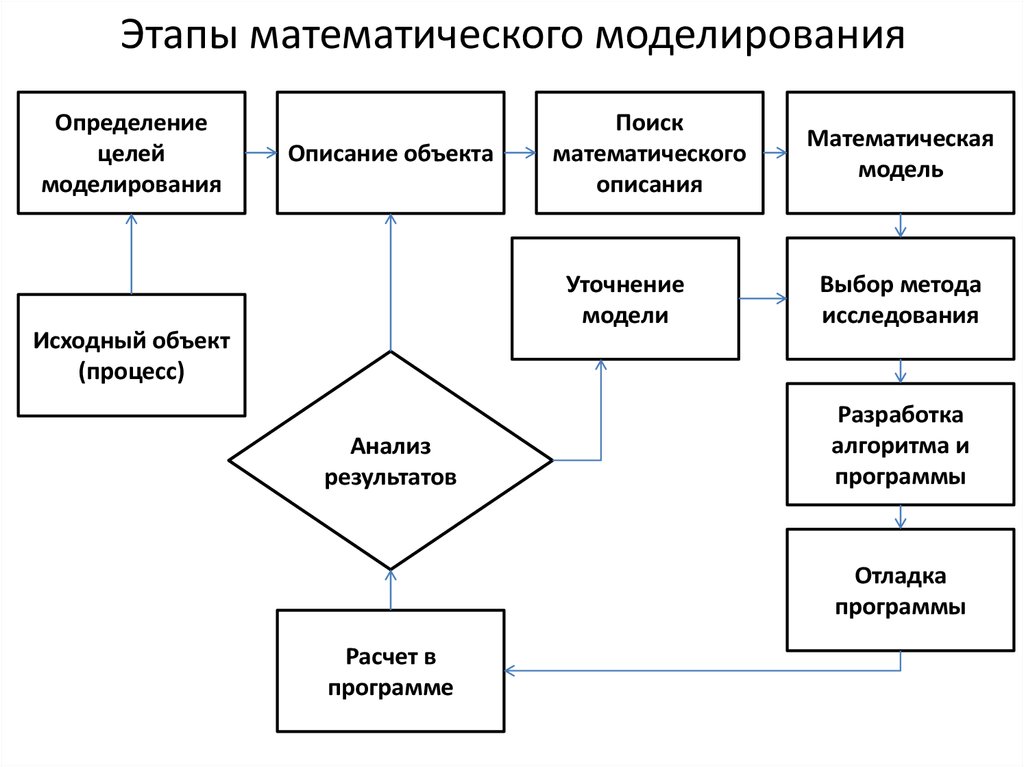
5. Этапы математического моделирования
Определениецелей
моделирования
Описание объекта
Поиск
математического
описания
Уточнение
модели
Математическая
модель
Выбор метода
исследования
Исходный объект
(процесс)
Анализ
результатов
Разработка
алгоритма и
программы
Отладка
программы
Расчет в
программе
6. Описание этапов ММ
Первый этап — определение целей моделирования (определениеструктуры и взаимосвязи, для управления, и прогнозирования).
Второй этап: определение входных и выходных параметров модели;
разделение входных параметров по степени важности влияния их
изменений на выходные.
Третий этап: построение математической модели. На этом этапе происходит
переход от абстрактной формулировки модели к формулировке,
имеющей конкретное математическое представление.
Четвертый этап: выбор метода исследования математической модели.
Чаще всего здесь используются численные методы, которые хорошо
поддаются программированию.
Пятый этап: разработка алгоритма, составление и отладка программы —
трудно формализуемый процесс.
Шестой этап: отладка программы. Работа программы проверяется на
тестовой задаче с заранее известным ответом.
Седьмой этап: собственно вычислительный эксперимент, в процессе
которого выясняется, соответствует ли модель реальному объекту
(процессу).
7. Используя аппарат теории множеств, транспортный процесс рассматривается на базе модели как совокупность следующих составляющих:
MTP X , Y , Z , E , Lгде X – входящие воздействия, которые могут быть изменены в
процессе принятия решения по совершенствованию
транспортного процесса;
Y – критерии эффективности транспортного процесса;
Z – влияния внешней среды, которые не могут быть изменены
в процессе принятия решения, но должны быть при этом
учтены;
E – составляющие элементы транспортного процесса;
L – связи между элементами транспортного процесса.
8. Характеристика {Е} составляющего.
Составляющие элементы системы {Е},описывающие транспортный процесс, являются
подпроцессами, из которых состоит
технологический процесс.
При этом описание элементов системы
осуществляется на основании многочисленных
показателей, являющихся характеристиками
соответствующих подпроцессов.
В качестве этих показателей могут быть,
например, время и себестоимость.
9. Характеристика {L} составляющего.
Связи между элементами транспортного процесса в моделях описываются спомощью функциональных зависимостей или алгоритмов. Наличие
зависимости свидетельствует о наличии связи и наоборот. Множество
связей {L} содержит в себе четыре подмножества:
• связи между управляемыми входящими факторами - являются
элементами системы (LXE): позволяют численно описать влияние
управляемых входящих параметров на многочисленные характеристики
отдельных подпроцессов;
• связи между входящими факторами, описывающие воздействие внешней
среды, и элементами системы (LZE): позволяют численно описать влияние
параметров внешней среды на характеристики отдельных технологических
процессов;
• связи между элементами системы (LEE): позволяют численно описать
взаимное влияние подпроцессов;
• связи между элементами системы и показателями, отражающими
эффективность ее функционирования (LEY): позволяют численно описать
влияние характеристик отдельных элементов системы на общий результат
функционирования.
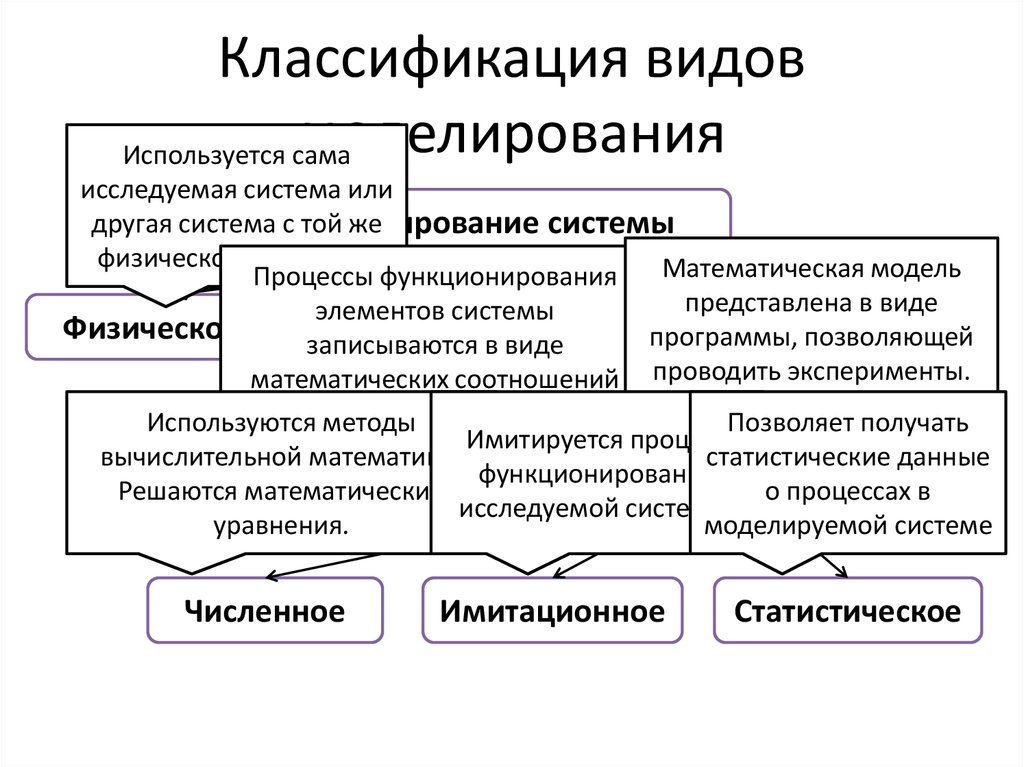
10. Классификация видов моделирования
Используется самаисследуемая система или
другая система сМоделирование
той же
системы
физической природой.
Математическая модель
Процессы функционирования
представлена в виде
элементов системы
Физическое
Математическое
программы, позволяющей
записываются в виде
математических соотношений проводить эксперименты.
Используются методы
Позволяет получать
Имитируется
процесс
Аналитическое
Компьютерное
вычислительной
математики.
статистические данные
функционирования
Решаются математические
о процессах в
исследуемой системы.
уравнения.
моделируемой системе
Численное
Имитационное
Статистическое
11. Математическое моделирование позволяет достичь следующих результатов:
1) соединить достоинства традиционных творческих иэкспериментальных методов;
2) исследовать такие системы, натурное и физическое
моделирование которых экономически не оправдано
и трудноосуществимо;
3) гарантировать высокую эффективность применения
вычислительной техники и существующих программ;
4) исследовать перспективные системы на стадии их
проектирования;
5) исследовать труднодоступные или ненаблюдаемые
объекты.
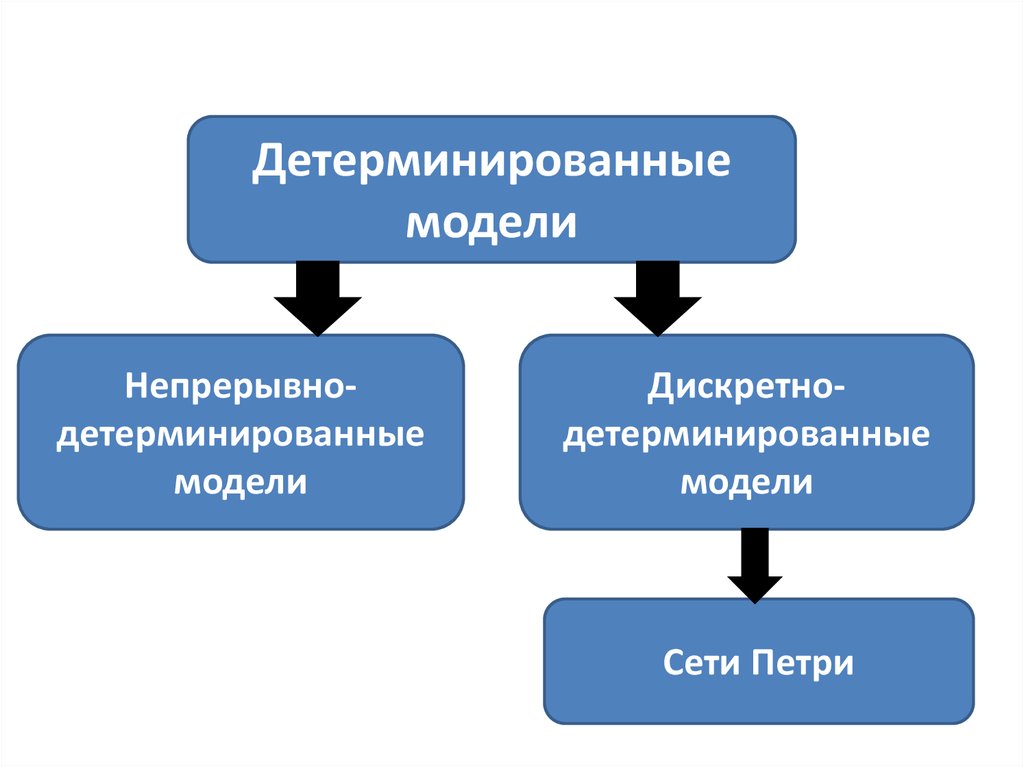
12. 2. Детерминированные модели.
Детерминированная модель [deterministicmodel] — аналитическое представление
закономерности, операции и т.п., при
которых для данной совокупности входных
значений на выходе системы может быть
получен единственный результат.
Такая
модель
может
отображать
как вероятностную систему (тогда она
является некоторым ее упрощением), так
и детерминированную систему.
13.
Детерминированныемодели
Непрерывнодетерминированные
модели
Дискретнодетерминированные
модели
Сети Петри
14. Непрерывно-детерминированные модели
Непрерывнодетерминированные моделиВ данной модели время t полагается
непрерывной переменной, а случайным
фактором пренебрегают. Основной
Переменная,
может
математический
аппарат которая
– теория
принимать любые значения,
дифференциальных
интегральных
т. е., неиограничена
какимлибо определенным
уравнений.
набором значений
15. Дискретно-детерминированные модели
В данных моделях время t являетсядискретной переменной: t=τΔ, где Δ – шаг
дискретизации, τ=0, 1, 2,… - «дискретное
Переменная, которая
время».
принимать только
Используемыйможет
математический
аппарат –
строго определенные
теория разностных уравнений
и
аппарат
значения
дискретной математики.
16.
Разностные уравнения – это уравнения,содержащие конечные разности искомой
функции
Ф( x , x 1,..., x n , u , u 1,..., u m , , ) 0,
где хτ=х(τΔ), uτ=u(τΔ) – соответственно
состояние системы и внешнее воздействие в
«дискретный момент времени τ».
17. 3. Математические модели и моделирование
Математическая модель – совокупность математических зависимостей,которые описывают с определённой степенью точности существующие в
окружающем мире процессы.
Математическое моделирование – определение характеристик и свойств
процесса или явления с помощью математической модели.
Типы математических моделей
Аналитические
Численные
Аналитическая математическая модель описывает процесс явным
аналитическим выражением, формулой, соотношением.
Численная математическая модель не имеет аналитического выражения
для описания процесса, однако описывается определённым
(итерационным) алгоритмом.
18.
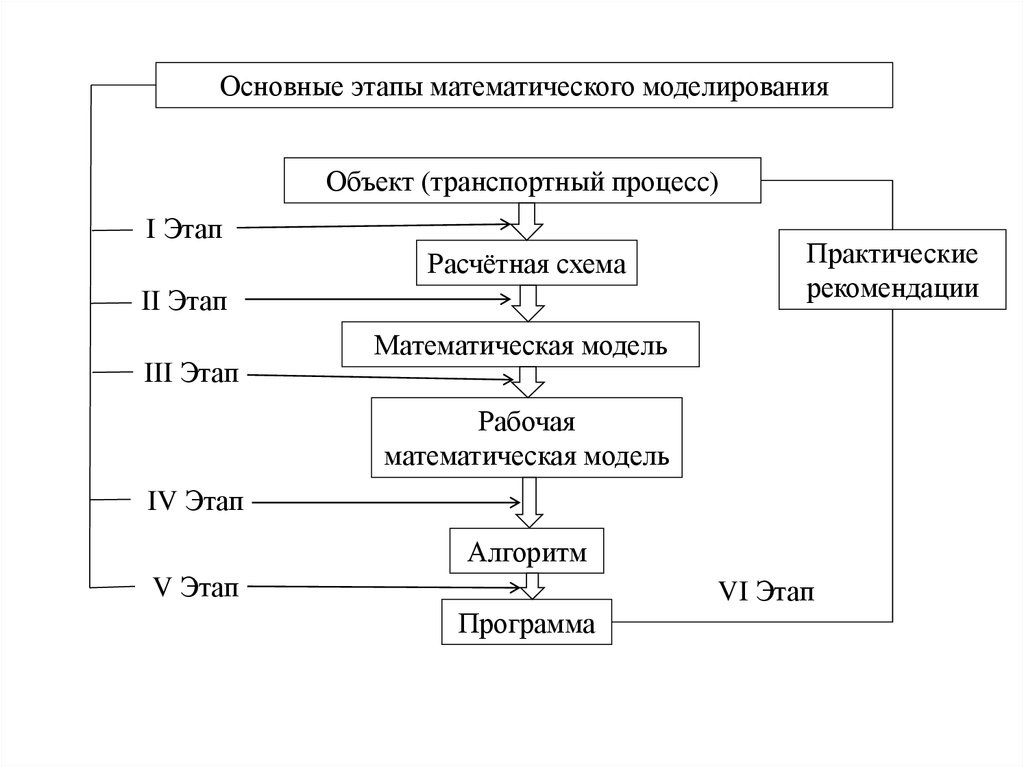
Основные этапы математического моделированияОбъект (транспортный процесс)
I Этап
Расчётная схема
II Этап
III Этап
Практические
рекомендации
Математическая модель
Рабочая
математическая модель
IV Этап
Алгоритм
V Этап
VI Этап
Программа
19.
На первом этапе математического моделирования осуществляетсяпереход от объекта моделирования к расчётной схеме. Расчётная
схема – это содержательная или (и) концептуальная модель
объекта. Например: план перевозки грузов, маршрутная карта,
транспортная таблица и т.д.
На втором этапе осуществляется поиск и формализованное
описание процесса (процессов) расчётной схемы математической
моделью.
На третьем этапе выполняется качественный и количественный
анализ математической модели включающий: 1) упрощение, 2)
разрешение противоречий, 3) коррекция.
На четвёртом этапе разрабатывается эффективный алгоритм
математического моделирования, по которому на пятом этапе
создаётся программа для реализации математического
моделирования.
На шестом этапе выполняется получение практических
рекомендаций путём использования программы. Практические
рекомендации – это результат использования математической
модели для конкретной цели при исследовании объекта
(транспортного процесса).
20.
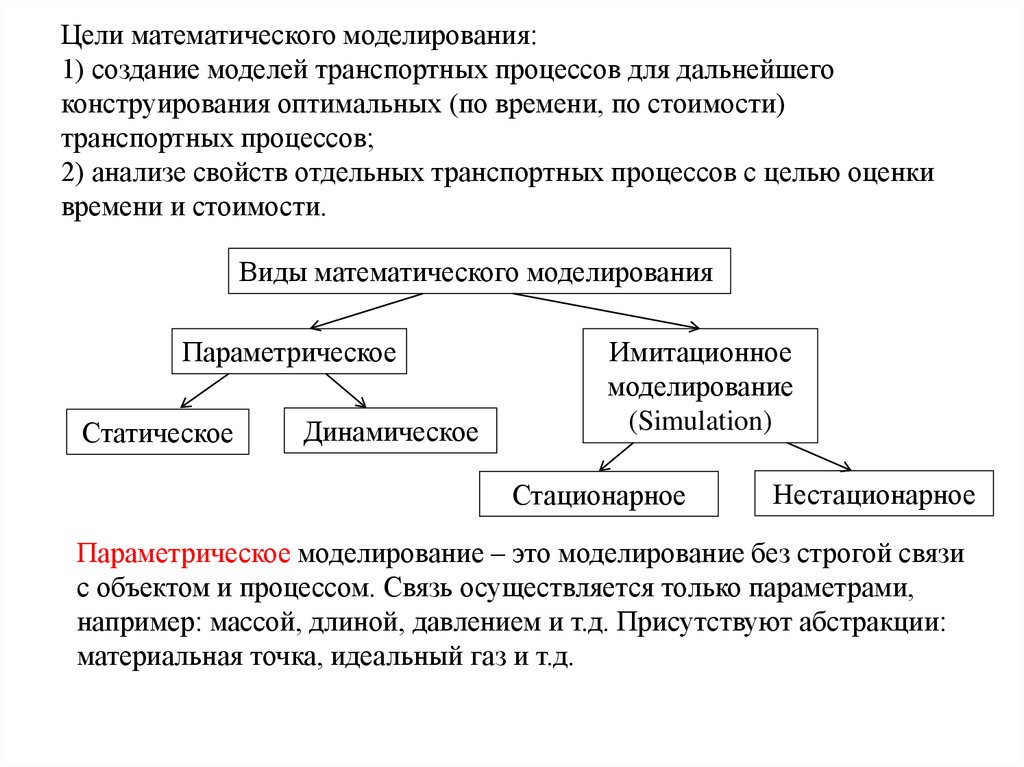
Цели математического моделирования:1) создание моделей транспортных процессов для дальнейшего
конструирования оптимальных (по времени, по стоимости)
транспортных процессов;
2) анализе свойств отдельных транспортных процессов с целью оценки
времени и стоимости.
Виды математического моделирования
Параметрическое
Статическое
Динамическое
Имитационное
моделирование
(Simulation)
Стационарное
Нестационарное
Параметрическое моделирование – это моделирование без строгой связи
с объектом и процессом. Связь осуществляется только параметрами,
например: массой, длиной, давлением и т.д. Присутствуют абстракции:
материальная точка, идеальный газ и т.д.
21.
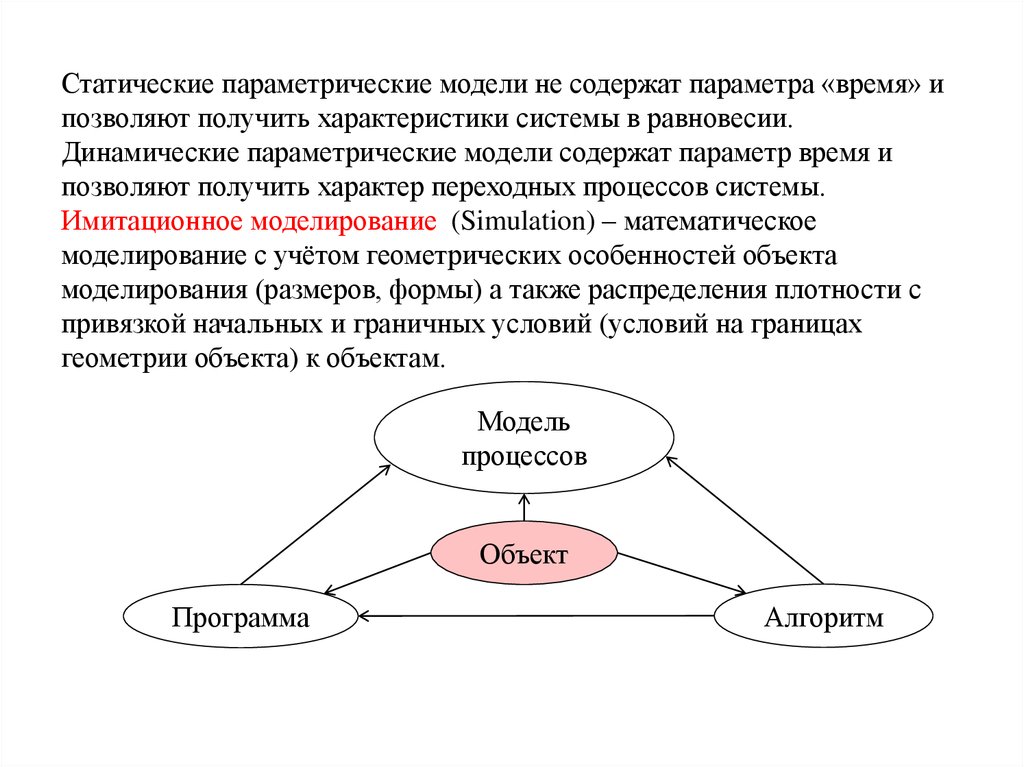
Статические параметрические модели не содержат параметра «время» ипозволяют получить характеристики системы в равновесии.
Динамические параметрические модели содержат параметр время и
позволяют получить характер переходных процессов системы.
Имитационное моделирование (Simulation) – математическое
моделирование с учётом геометрических особенностей объекта
моделирования (размеров, формы) а также распределения плотности с
привязкой начальных и граничных условий (условий на границах
геометрии объекта) к объектам.
Модель
процессов
Объект
Программа
Алгоритм
22.
Стационарное моделирование позволяет получить характеристикиобъекта в интервале времени стремящемся к нулю, то есть
«сфотографировать» характеристики объекта. Нестационарное
моделирование позволяет получить характеристики объекта с течением
времени.
Структура математической модели
Входные параметры
Уравнения,
зависимости и т.д.
Выходные параметры
Свойства математической модели:
1) Полнота – степень отражения известных свойств объекта;
2) Точность – порядок совпадения реальных (экспериментальных) и
найденных с помощью модели характеристик;
3) Адекватность – это способность модели описывать выходные
параметры с фиксированной точностью для фиксированных входных
параметров (область адекватности).
23.
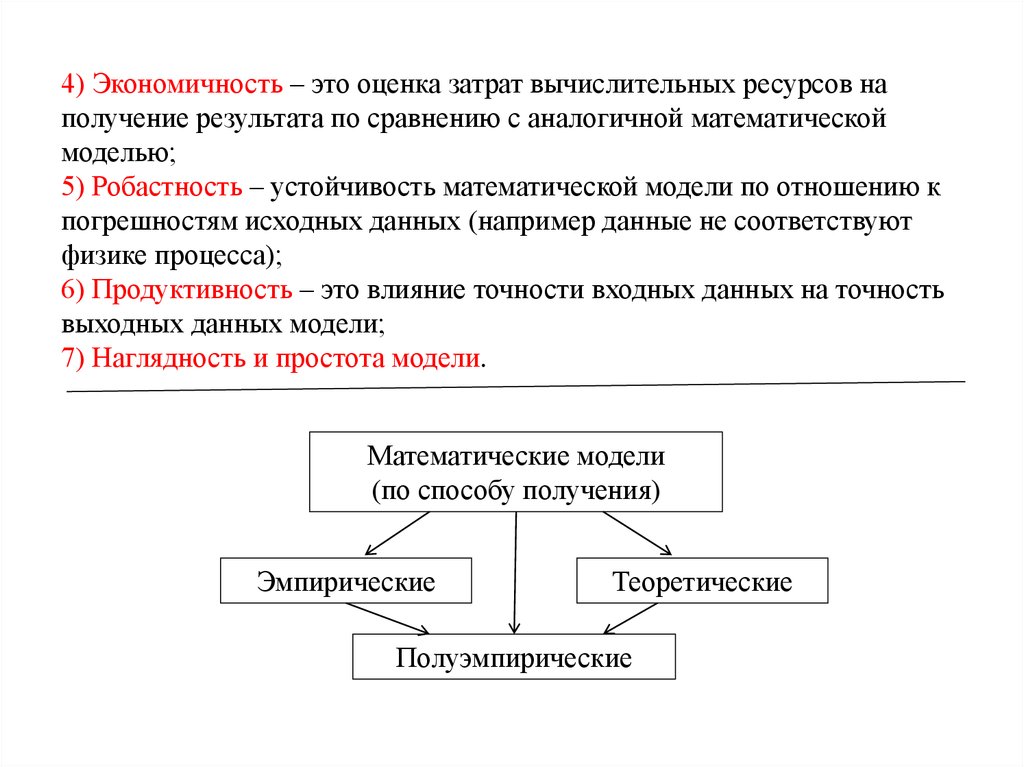
4) Экономичность – это оценка затрат вычислительных ресурсов наполучение результата по сравнению с аналогичной математической
моделью;
5) Робастность – устойчивость математической модели по отношению к
погрешностям исходных данных (например данные не соответствуют
физике процесса);
6) Продуктивность – это влияние точности входных данных на точность
выходных данных модели;
7) Наглядность и простота модели.
Математические модели
(по способу получения)
Эмпирические
Теоретические
Полуэмпирические
24.
Эмпирические математические модели получают путёмобработки и анализа результатов экспериментальных
данных. Идентификация – коррекция существующей
математической модели эмпирическими данными.
Теоретические математические модели получают
теоретическими методами – анализ, синтез, индукция,
дедукция и т.д.
25. Тема лекции № 1.2
Принципыимитационного
моделирования
транспортных
процессов.
25
26. Цель лекции – изучить основные принципы имитационного моделирования транспортных процессов
План лекции.1. Имитационное моделирование и
условия его применения.
2. Понятие модельного времени.
3. Способы имитации.
4. Этапы имитационного моделирования.
26
27. 1. Имитационное моделирование и условия его применения.
Имитационное моделирование - это методисследования, при котором изучаемая
система
заменяется
моделью
с
достаточной
точностью
описывающей
реальную систему и с ней проводятся
эксперименты
с
целью
получения
информации об этой системе.
Экспериментирование с моделью называют
имитацией (имитация это постижение
сути
явления,
не
прибегая
к
экспериментам на реальном объекте).
27
28.
Имитационнаямодель
логикоматематическое описание объекта, которое
может
быть
использовано
для
экспериментирования на компьютере в целях
проектирования,
анализа
и
оценки
функционирования объекта.
Условие использования.
Существует класс объектов, для которых по
различным причинам, не разработаны
аналитические модели либо не разработаны
аналитические методы решения полученной
модели. В таких случаях математическая
модель заменяется имитатором или
имитационной моделью.
28
29. Достоинства имитационного моделирования
1. Высокая адекватность между физической сущностьюописываемого процесса и его моделью.
2. Возможность описать сложную систему на достаточно
высоком уровне детализации.
3. Значительно большие охват исследования, чем
аналитическое моделирование.
4. Отсутствие ограничений на зависимости между
параметрами модели.
5. Возможность оценки функционирования системы не
только в стационарных состояниях, но и в переходных
процессах (режимах).
6. Получение большого числа данных об исследуемом
объекте (закон распределения случайных величин,
числовые значения абсолютные и относительные, и
многое другое).
7. Наиболее рациональное отношение «результат –
затраты» по отношению к аналитическому и
физическому моделированию.
29
30. Недостатки имитационного моделирования
1. Относительно большая сложность создания модели.2. Необходимость высокой квалификации исследователя
для написания модели.
3. Необходимость проведения верификации и валидации
данных моделирования.
Верификация (от лат. verus «истинный» и facere «делать») это
подтверждение соответствия конечного продукта
предопределённым эталонным требованиям.
Валидация (англ. Validation) - подтверждение на основе представления
объективных свидетельств того, что требования, предназначенные
для конкретного использования или применения, точно и в полном
объёме предопределены, а цель достигнута.
4. Индивидуальность реализации. Для широкого
применения моделью можно воспользоваться лишь при
детальном описании ее построения.
5. Не существует надежных методов оценки адекватности.
30
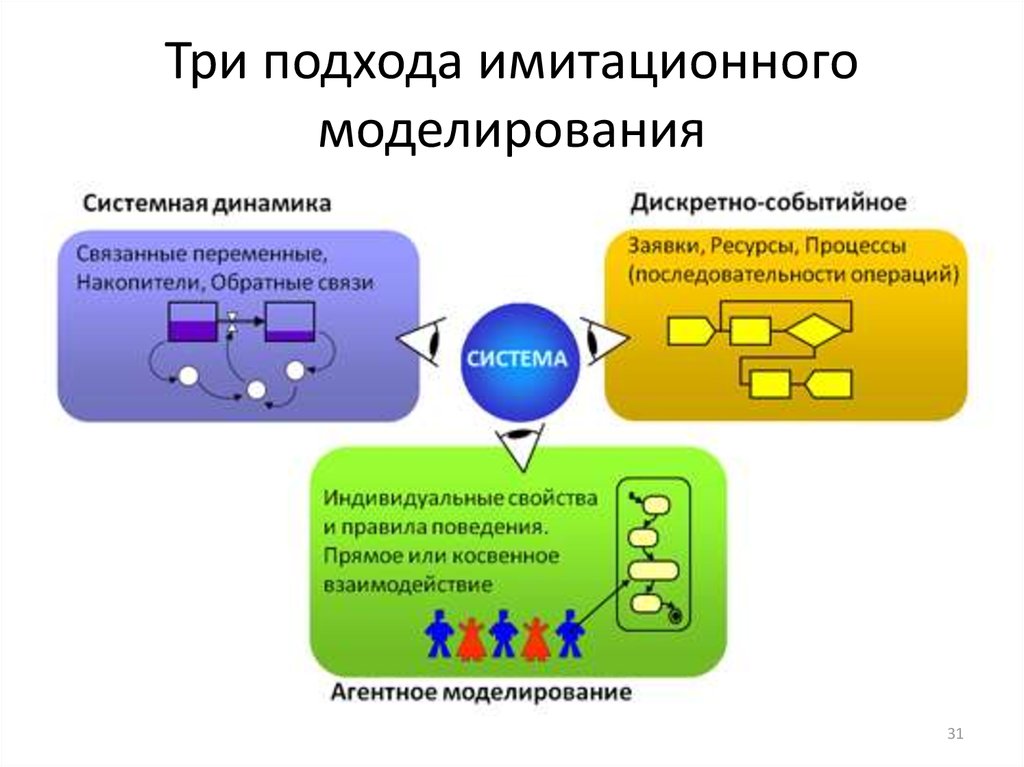
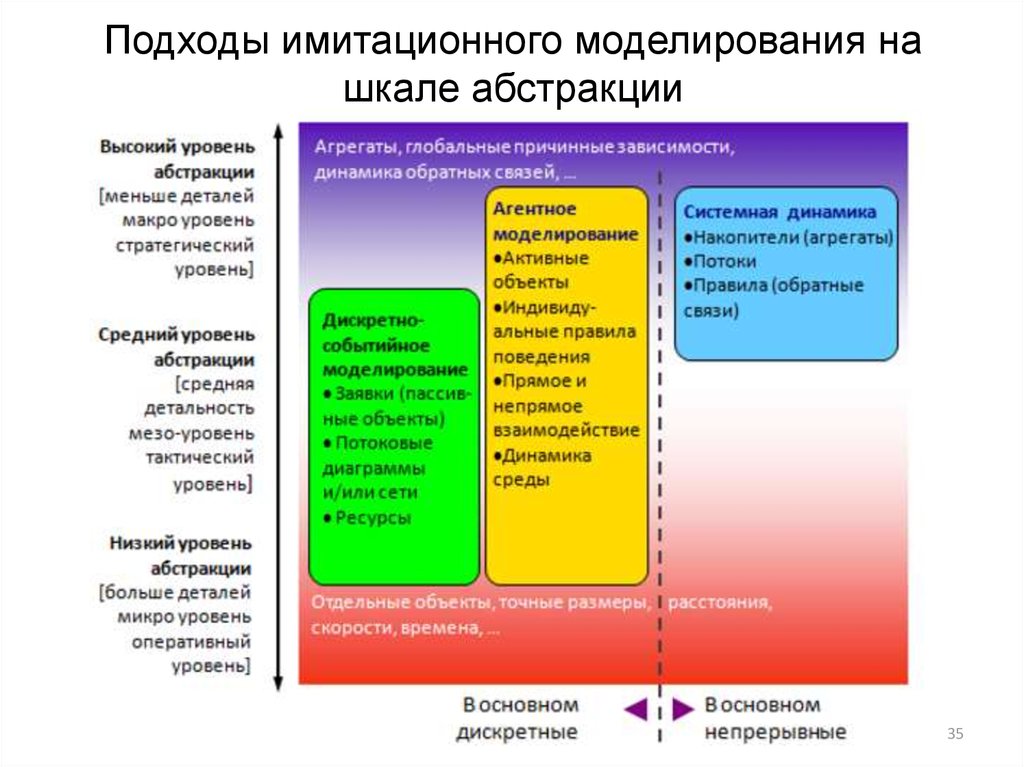
31. Три подхода имитационного моделирования
3132. Виды имитационного моделирования
1. Агентное моделирование — метод имитационногомоделирования, исследующий поведение
децентрализованных агентов и то, как такое поведение
определяет поведение всей системы в целом.
Цель агентных моделей — получить представление об
этих глобальных правилах, общем поведении системы,
исходя из предположений об индивидуальном,
частном поведении её отдельных активных объектов и
взаимодействии этих объектов в системе.
Агент — некая сущность, обладающая активностью,
автономным поведением, может принимать решения в
соответствии с некоторым набором правил,
взаимодействовать с окружением, а также
самостоятельно изменяться.
32
33. Виды имитационного моделирования
2. Дискретно-событийное моделирование —подход к моделированию, предлагающий
абстрагироваться от непрерывной природы
событий и рассматривать только основные
события моделируемой системы, такие, как:
«ожидание», «обработка заказа», «движение с
грузом», «разгрузка» и другие.
Дискретно-событийное моделирование наиболее
развито и имеет огромную сферу
приложений — от логистики и систем
массового обслуживания до транспортных и
производственных систем.
Этот вид моделирования наиболее подходит для
моделирования транспортных процессов.
33
34. Виды имитационного моделирования
3. Системная динамика — парадигмамоделирования, где для исследуемой системы
строятся графические диаграммы причинных
связей и глобальных влияний одних параметров
на другие во времени, а затем созданная на
основе этих диаграмм модель имитируется на
компьютере.
Данный вид моделирования более всех других
парадигм помогает понять суть происходящего
выявления причинно-следственных связей
между объектами и явлениями.
С помощью системной динамики строят модели
бизнес-процессов, развития города, модели
производства, динамики популяции, экологии
34
35. Подходы имитационного моделирования на шкале абстракции
3536. 2. Понятие модельного времени.
Особенности функционирования компьютерных программ,которые приходится учитывать при разработке
имитационных моделей (ИМ):
1. Сложная система S, как правило, состоит из многих
элементов, которые функционируют одновременно.
При этом параллельное выполнение нескольких
программ, имитирующих поведение отдельных
элементов, невозможно.
2. ИМ должны оперировать с конечным множеством
данных и, следовательно, имитировать поведение
системы S не во все моменты времени, а лишь в
некоторые, составляющие конечное множество
[0, T ],
где
- означает мощность множества
36
37.
Системное модельное время или модельное время(МВ) – специальная переменная t, используемая
для обеспечения имитации параллельных или
одновременных событий системы S на конечном
множестве моментов времени .
Способы формирования конечного множества
моментов времени (принципы изменения МВ):
1. «Принцип ∆t» заключается в изменении МВ с
фиксированным шагом ∆t.
2. «Принцип ∆х» заключается в изменении МВ при
скачкообразном изменении вектора состояния х
системы S на некоторую величину ∆х (∆х≠0).
37
38.
Особенности принципов.Пусть система S состоит из N элементов: А(1), …, А(N),
поведение которых предполагается моделировать:
S={А(1), …, А(N)}.
Для каждого элемента A(i) S (i 1,..., N )
(i )
Определим локальное модельное время (ЛМВ) t [0, T ]
Поведение элемента A(i) в течение интервала
моделирования определяется некоторой
последовательностью действий
(i )
g1(i ) , g 2(i ) ,..., g M
, g (ji ) G, j 1,..., M i
где G – множество всевозможных действий для элементов
S.
На множестве G будем выделять подмножество действий
D G
D:
для выполнения которых в ИМ требуется некоторое
ненулевое модельное время.
38
39.
Будем обозначать такие действияd1(i ) ,..., d m(i ) , (d (ji ) D G, j 1, mi , mi M i , i 1, N )
i
а интервалы МВ, затрачиваемые на выполнение этих
(i )
(i )
,...,
действий, соответственно: 1
mi .
(i )
{
Последовательность
j } ( j 1, mi )
является последовательностью случайных величин с
(i )
заданными законами распределения L{ j }, i 1, N
(i )
A
äëÿ Aj S
Момент ЛМВ наступления события
j
t (j i ) t * (j i ) , j 1,2,...
где j имитируется в соответствии с законом
(i )
распределения L{ j } , t* - текущее значение МВ.
(i )
39
40.
Состояниевремени t [0,T ]
системы
S
в
определяется вектором состояния
момент
x(t ) X Rn .
t (j i )
Состояния системы в моменты
наступления особых
событий будем называть особыми состояниями, а состояние
х(0) —начальным состоянием системы.
Случаи выбора «принципа Δt»
1) если Δt — мало, то выполняется много лишних вычислений
состояний системы в моменты, когда вектор z(t) не изменяется (за
счет этого возрастает машинное время имитации);
2) даже при сравнительно малом значении Δt моменты наступления
событий в системе (а, следовательно, и моменты изменения
состояния системы) не совпадают с моментами наступления
событий в ИМ, поэтому фазовая траектория, построенная с
помощью ИМ, на множестве t [0,T ] не совпадает с фазовой
траекторией системы S.
На практике предпочтение отдается принципу Δх.
40
41. Иллюстрация принципов «∆t» и «∆х»
A( 2)А(2)1
А(2)2
А(2)3
0
A(1)
t(2)1
0
А(1)1
t(2)2
t(1)1
t
А(1)2
t(1)2
∆ 2∆ 3∆ 4∆ 5∆ 6∆ 7∆
0
t(2)3
15∆
x
0
t(2)1
t(1)1
t(2)2
t(1)2
t(2)3
Рисунок 2.1 – Временная диаграмма
41
42. Рекомендация к применению
В большинстве практически важных случаев(i )
{
A
} наступают через случайные
события
j
i
интервалы времени {t j } . Поэтому способ задания
шага до следующего события экономичнее (в
смысле затрат машинного времени) и точнее (в
смысле точности аппроксимации) фазовой
траектории способа фиксированного изменения МВ.
По примеру, фазовая траектория системы S,
построенная с помощью ИМ, по принципу ∆х:
x(0), x(t1(2) ), x(t1(1) ), x(t2(2) ), x(t2(1) ), x(t3(2) ).
42
43. 3. Способы имитации.
Под способом имитации системы S понимают способформирования фазовой траектории системы.
Последний определяется способом изменения
вектора состояния x(t ), t J системы S.
Возможны три способа изменения х(t):
(i )
{
A
1) в моменты наступления события j };
(i )
2) в результате выполнения действий {d j }, на
выполнение которых требуются затраты модельного
(i )
{
};
времени
j
3) в результате выполнения хронологической
последовательности событий и действий,
называемой процессом.
43
44.
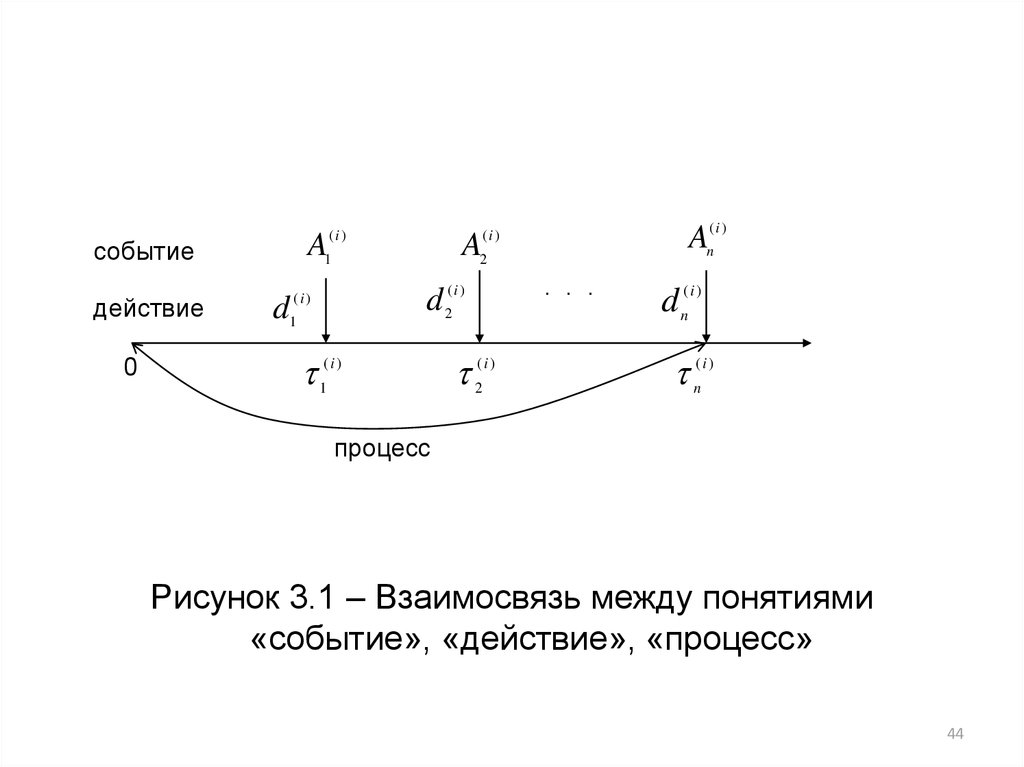
действие0
A2
A1
событие
d 2( i )
(i )
d1
An( i )
(i )
(i )
1( i )
2( i )
. . .
d n( i )
n( i )
процесс
Рисунок 3.1 – Взаимосвязь между понятиями
«событие», «действие», «процесс»
44
45.
В зависимости от того, какой из трех
способов формирования фазовой
траектории используется, различают
способы имитации:
событийный;
основанный на просмотре активностей;
процессный;
транзактный;
агрегатный.
45
46.
Событийный способ:1) множество особых событий можно разбить на
небольшое число L типов событий
N
{ A ,..., A } { Aj },( j 1, mi , i 1, N ), L mi ;
(1)
( L)
(i )
i 1
2) для каждого типа событий определена
последовательность действий, приводящая к
изменению состояния системы S;
3) определены условия перехода от одного события к
другому для всех типов событий;
4) интервалы времени между последовательными
наступлениями событий – случайные величины с
известными законами распределения вероятностей.
46
47.
Способ, основанный на просмотреактивностей:
1) все действия для элемента А(i) системы S
различны и приводят к наступлению
различных событий;
2) каждое действие d(i)j характеризуется
набором условий его выполнения;
3) времена выполнений действий {τ(i)j} являются
случайными величинами с известными
законами распределения вероятностей.
47
48.
Процессныйспособ
сочетает
особенности
событийного и способа, основанного на просмотре
активностей.
Применяется, когда поведение элементов А(i) системы S
может быть описано фиксированными для некоторого
класса систем последовательностями событий и
действий, так называемыми процессами.
Транзактный способ имитации сформирован в
результате развития процессного способа для
моделирования систем массового обслуживания.
Агрегатный способ основывается на использовании
агрегативных моделей.
48
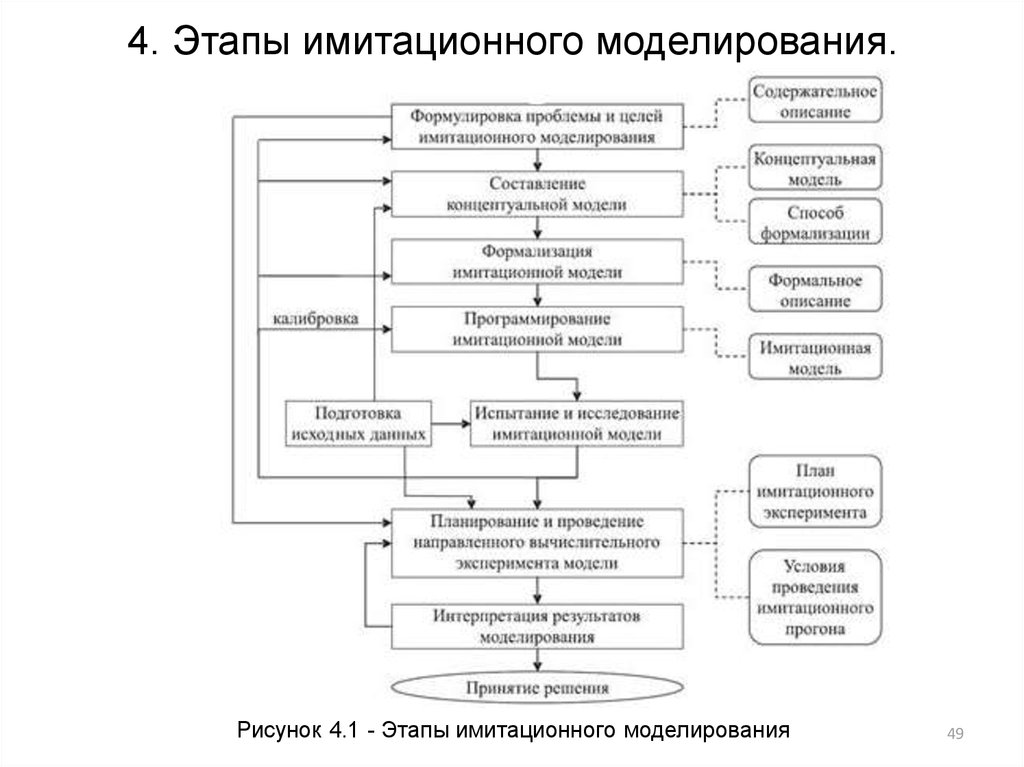
49. 4. Этапы имитационного моделирования.
Рисунок 4.1 - Этапы имитационного моделирования49
50.
Особенности этапов ИМ.1. Формулировка проблемы и определение целей
имитационного исследования. Документированным
результатом на этом этапе является составленное
содержательное описание объекта моделирования.
2. Разработка концептуального описания. Результатом
деятельности системного аналитика является
концептуальная модель (или вербальное описание) и
выбор способа формализации для заданного объекта
моделирования.
3. Формализация имитационной модели. Составляется
формальное описание объекта моделирования.
4. Программирование имитационной модели (разработка
программы-имитатора). На этапе осуществляется
выбор средств автоматизации моделирования,
алгоритмизация, программирование и отладка
имитационной модели.
50
51.
5. Испытание и исследование модели, проверкамодели. Проводится верификация модели, оценка
адекватности, исследование свойств имитационной
модели и другие процедуры комплексного
тестирования разработанной модели.
6. Планирование и проведение имитационного
эксперимента. На данном технологическом этапе
осуществляется стратегическое и тактическое
планирование имитационного эксперимента.
Результатом является составленный и
реализованный план эксперимента, заданные
условия имитационного прогона для выбранного
плана.
7. Анализ результатов моделирования. Проводится
интерпретация результатов моделирования и их
использование – собственно принятие решений.
51
52. Задача математического программирования
Переменные x1, х2, …, хnОграничения – уравнения или
неравенства, построенные в
соответствии с логическим
содержанием задачи.
Целевая функция (ЦФ) выражает
принятый критерий оптимальности.
Требуется найти такой набор значений
переменных, который удовлетворяет
системе ограничений и при котором
ЦФ принимает наибольшее или
наименьшее значение.
53. Задача математического программирования (линейный вид)
Z c1 x1 c2 x2 ... cn xn max(min)a11x1 a12 x2 ... a1n xn b1 ;
a
x
a
x
...
a
x
b
;
21
1
22
2
2
n
n
2
.............................................
a x a x ... a x b ;
mn n
m
m1 1 m 2 2
x j 0, i 1,2,...,m; j 1,2 ,...,n
54. Задача математического программирования (нелинейный вид)
Z f ( x1 , x2 ,...xn ) max(min)qi ( x1 , x2 ,...xn ) 0
x
0
,
i
1
,
2
,...,m;
j
1
,
2
,...,n
j
55.
Линейное программирование системаограничений
и
ЦФ
линейны относительно искомых
величин x1, х2, …, хn
Нелинейное
программирование
хотя
бы
одно
выражение.
- имеется
нелинейное
56.
План задачи - любаясовокупность численных значений
переменных.
План, удовлетворяющий
системе ограничений, называется
допустимым.
Допустимый план,
максимизирующий или
минимизирующий ЦФ, называется
оптимальным.
57.
Система ограничений,которой не отвечает ни одна
совокупность неотрицательных
значений переменных,
называется несовместной, т.е.
не имеет решения.
Совместной называется
система, имеющая хотя бы одно
допустимое решение.
58.
Методы стохастическогопрограммирования – исходные
параметры могут быть выражены
случайными числами.
Задачи, в которых нет
необходимости вычислять экстремум
на нескольких этапах, - одноэтапные
(статические).
Многоэтапные задачи требуют
применения динамического
программирования.
59.
Методы параметрическогопрограммирования – исходные
параметры могут изменяться в
определённых пределах.
Методы дискретного
программирования – параметры задач
могут принимать лишь ограниченное
число значений.
Также в экономических
исследованиях применяют и другие
количественные методы –
регрессионный, дисперсионный анализ,
межотраслевой баланс и т.д.
60. Лекция 2. Методы математического программирования.
План:1.
Графический метод решения задач линейного
программирования (ЗЛП)
2.
Симплексный метод решения ЗЛП
3.
Примеры решения ЗЛП в землеуправлении
61.
Графическое решение задач линейногопрограммирования
Задача линейного программирования с
двумя неизвестными может быть
решена графически
Замечание:
К такой форме может быть сведена и
каноническая задача (с ограничениями в
виде уравнений), когда число переменных n
больше числа уравнений m на 2
62.
Пусть задача линейного программированиязадана в виде:
63.
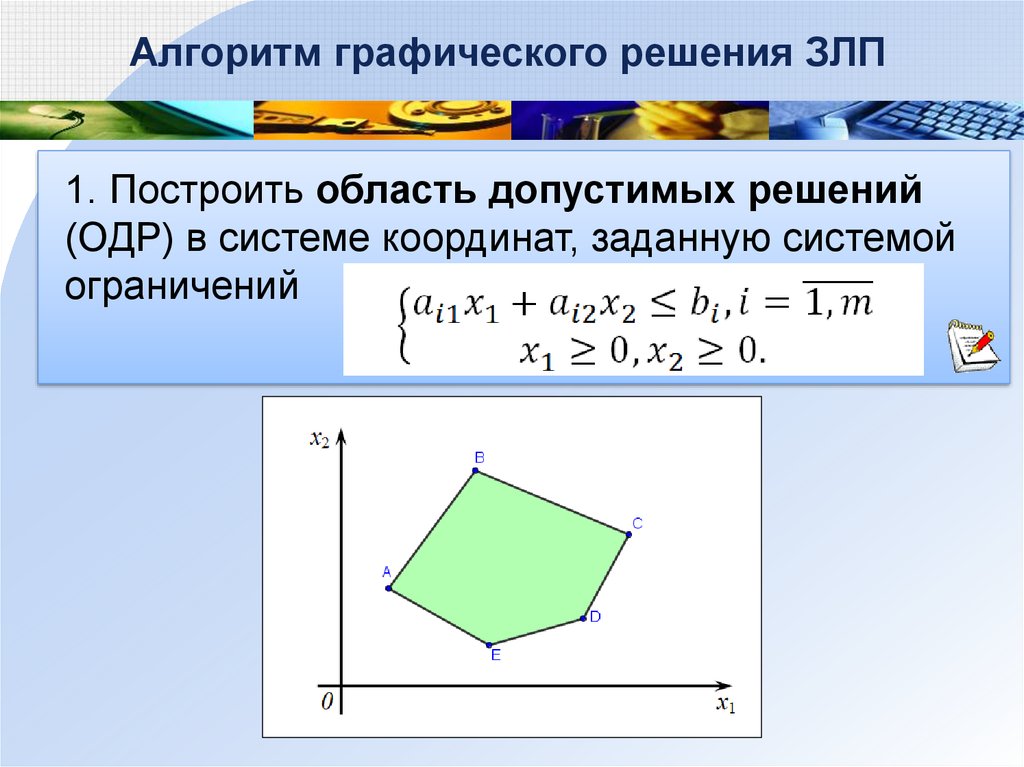
Алгоритм графического решения ЗЛП1. Построить область допустимых решений
(ОДР) в системе координат, заданную системой
ограничений
64.
Алгоритм графического решения ЗЛП2. Построить градиент целевой функции
F = с1х1+с2х2
(вектор нормали (вектор градиента) к прямой
с1х1+с2х2 = F)
65.
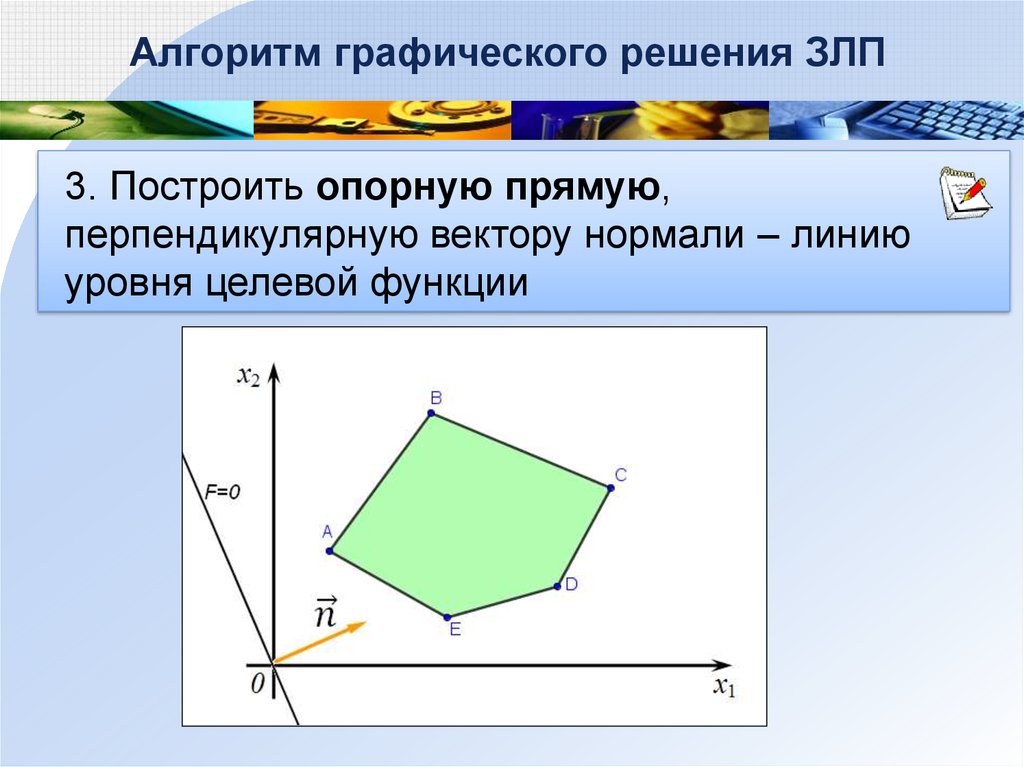
Алгоритм графического решения ЗЛП3. Построить опорную прямую,
перпендикулярную вектору нормали – линию
уровня целевой функции
66.
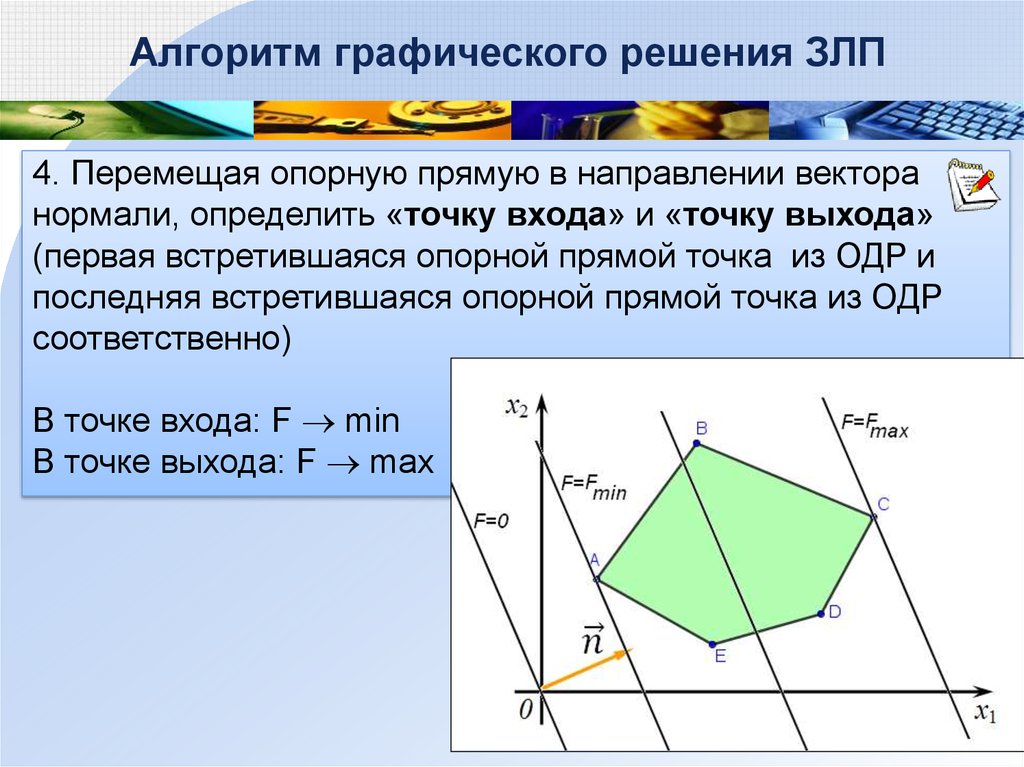
Алгоритм графического решения ЗЛП4. Перемещая опорную прямую в направлении вектора
нормали, определить «точку входа» и «точку выхода»
(первая встретившаяся опорной прямой точка из ОДР и
последняя встретившаяся опорной прямой точка из ОДР
соответственно)
В точке входа: F min
В точке выхода: F max
67.
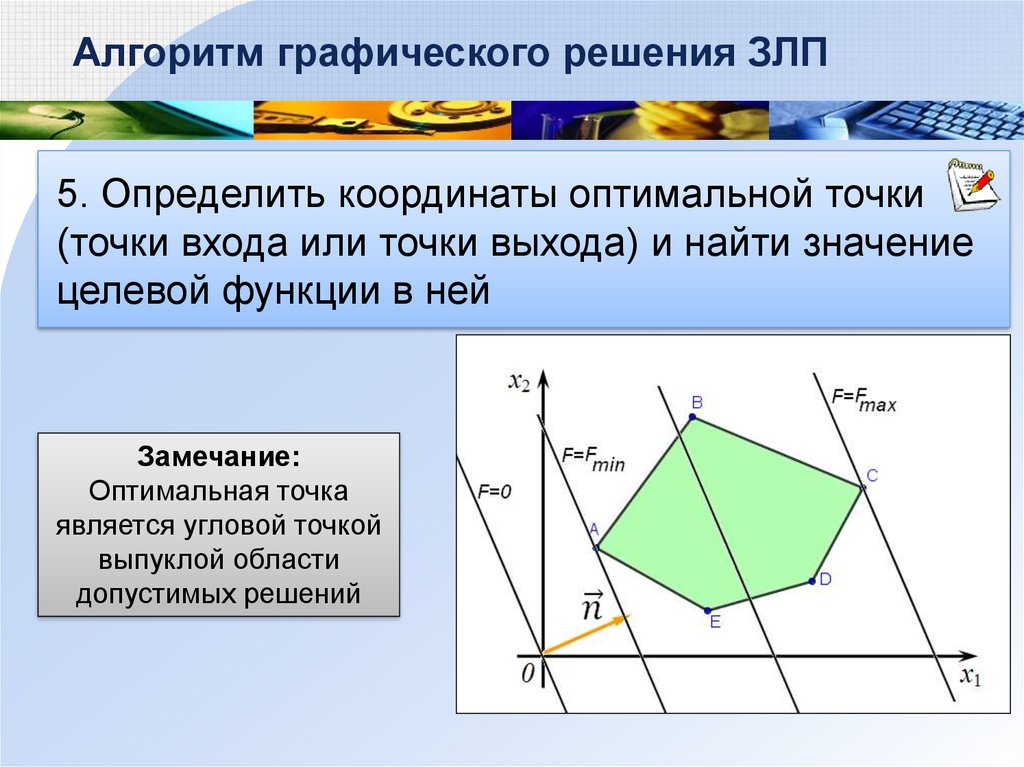
Алгоритм графического решения ЗЛП5. Определить координаты оптимальной точки
(точки входа или точки выхода) и найти значение
целевой функции в ней
Замечание:
Оптимальная точка
является угловой точкой
выпуклой области
допустимых решений
68.
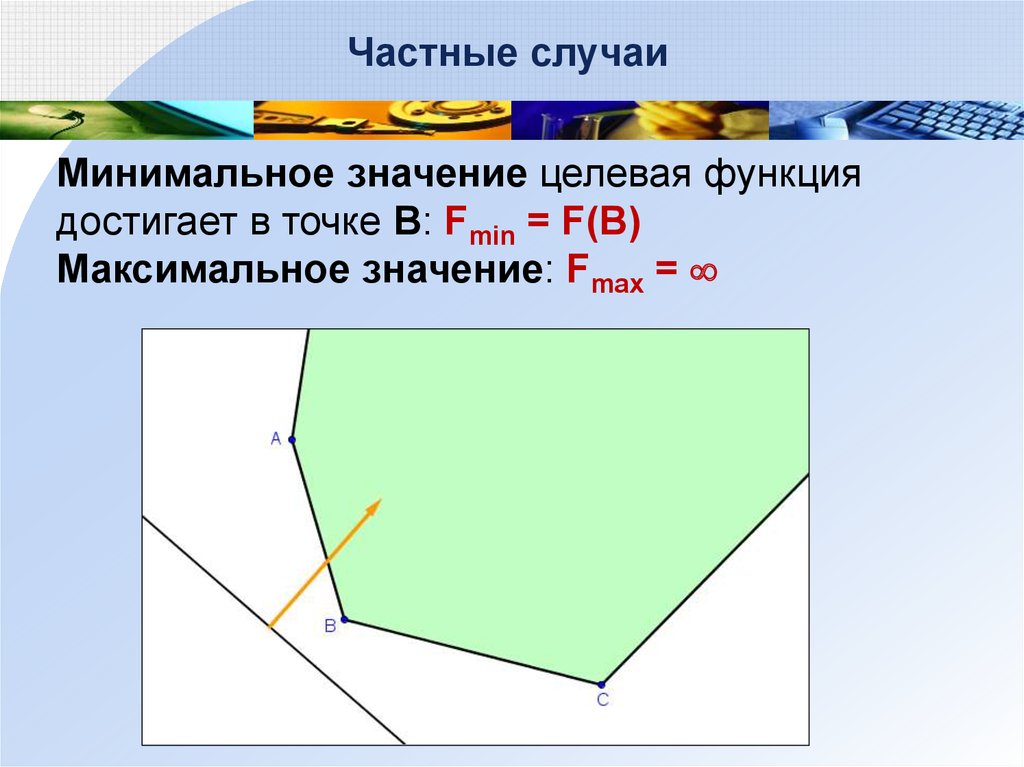
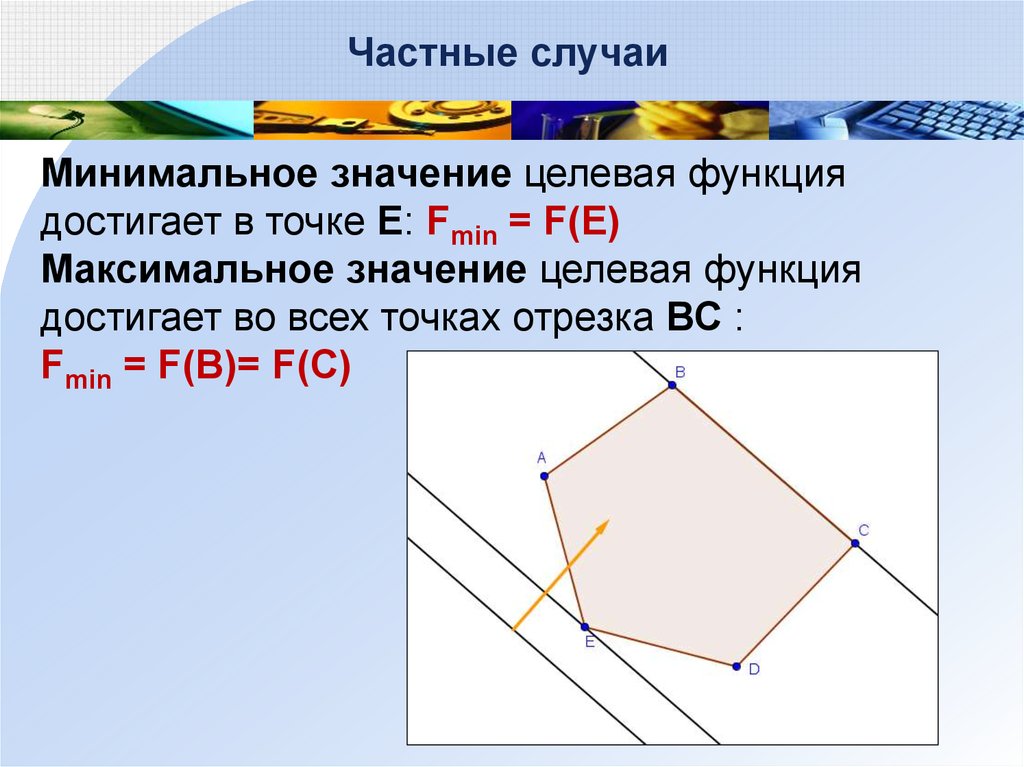
Частные случаиМинимальное значение целевая функция
достигает в точке В: Fmin = F(B)
Максимальное значение: Fmax =
69.
Частные случаиМинимальное значение целевая функция
достигает в точке E: Fmin = F(E)
Максимальное значение целевая функция
достигает во всех точках отрезка ВС :
Fmin = F(B)= F(C)
70.
ВСПОМНИМЛинейное неравенство
a1x1+a2x2 b
на плоскости задает полуплоскость,
границей которой является прямая
a1x1+a2x2=b
71.
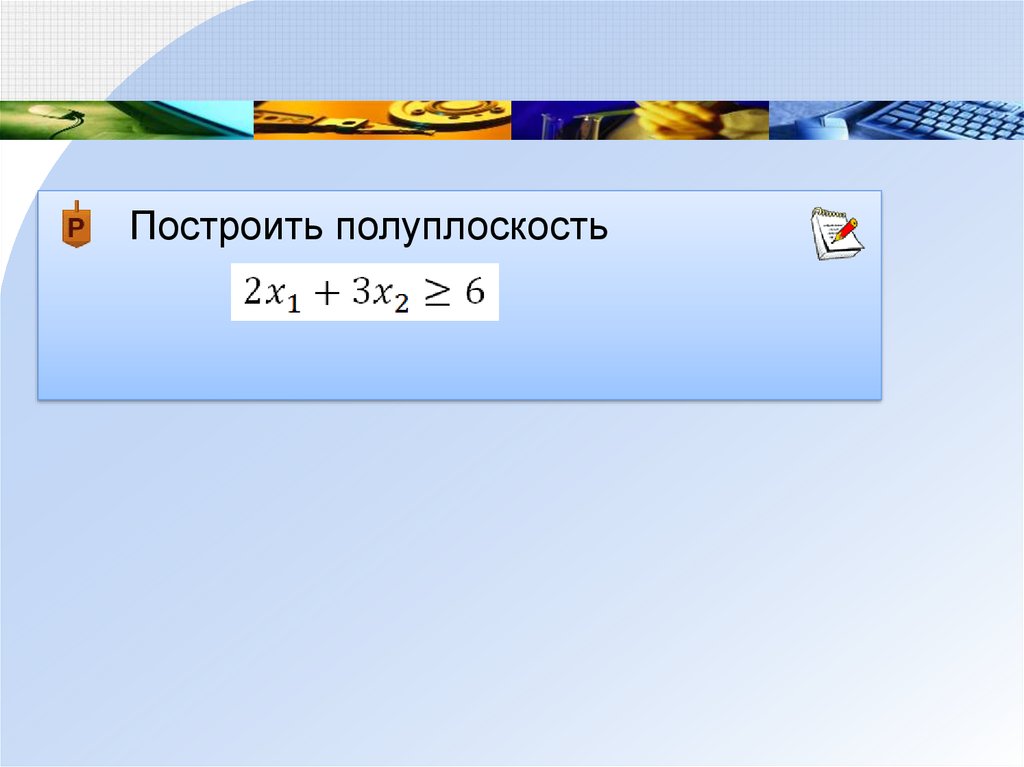
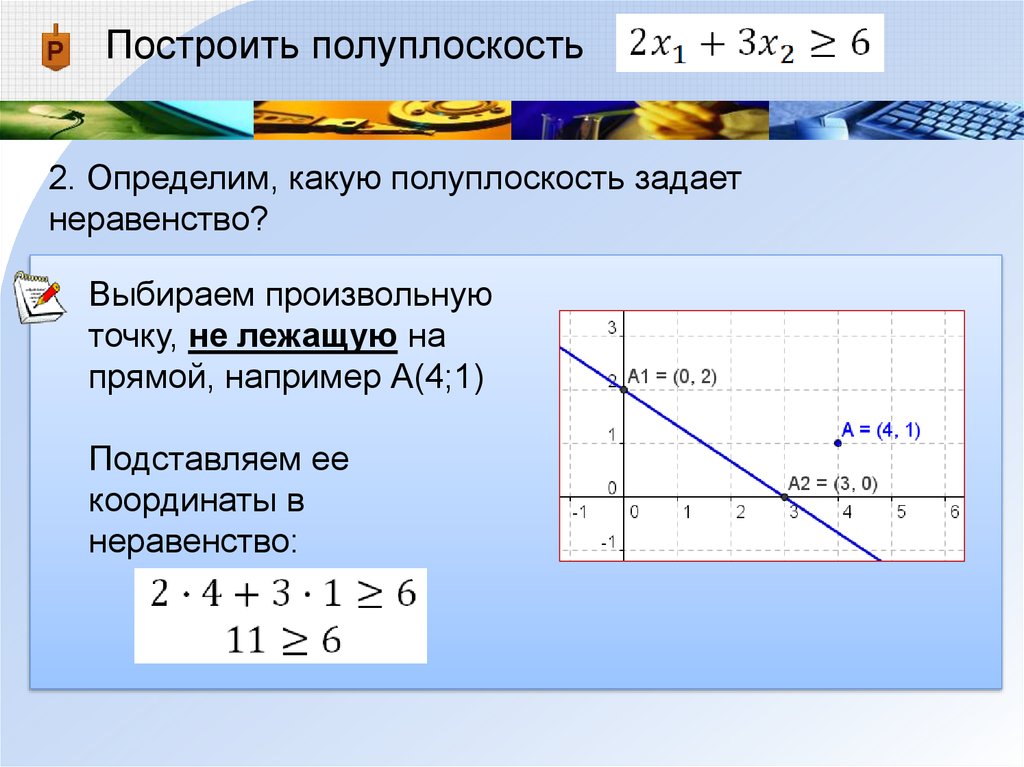
Построить полуплоскость72.
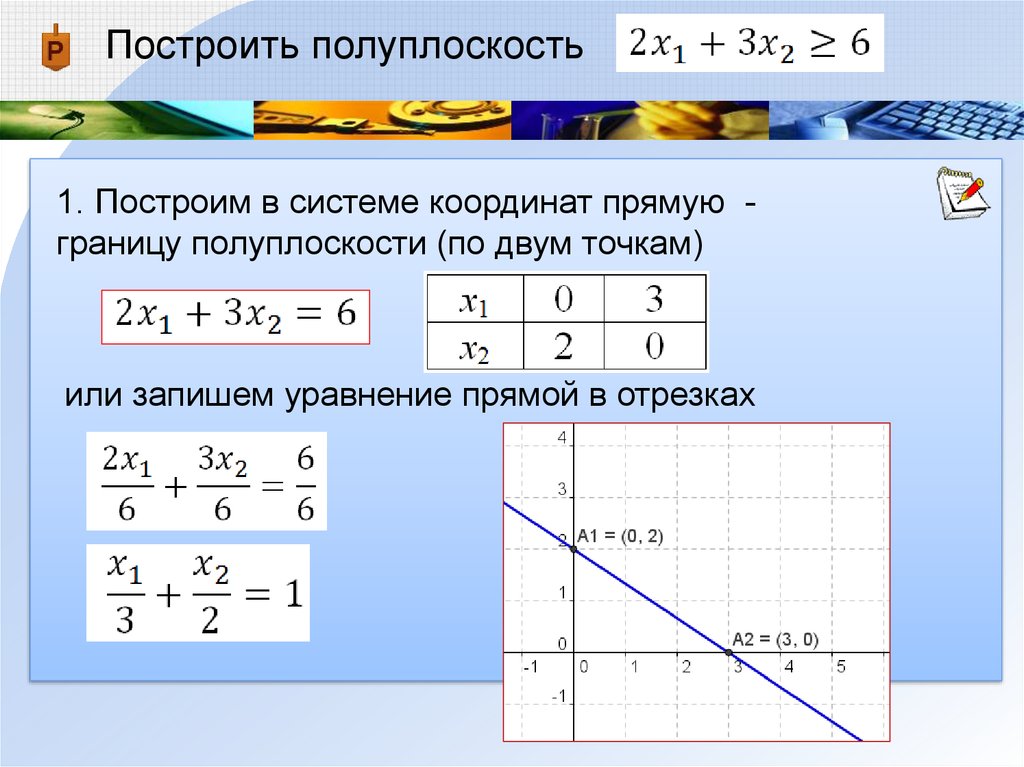
Построить полуплоскость1. Построим в системе координат прямую границу полуплоскости (по двум точкам)
или запишем уравнение прямой в отрезках
73.
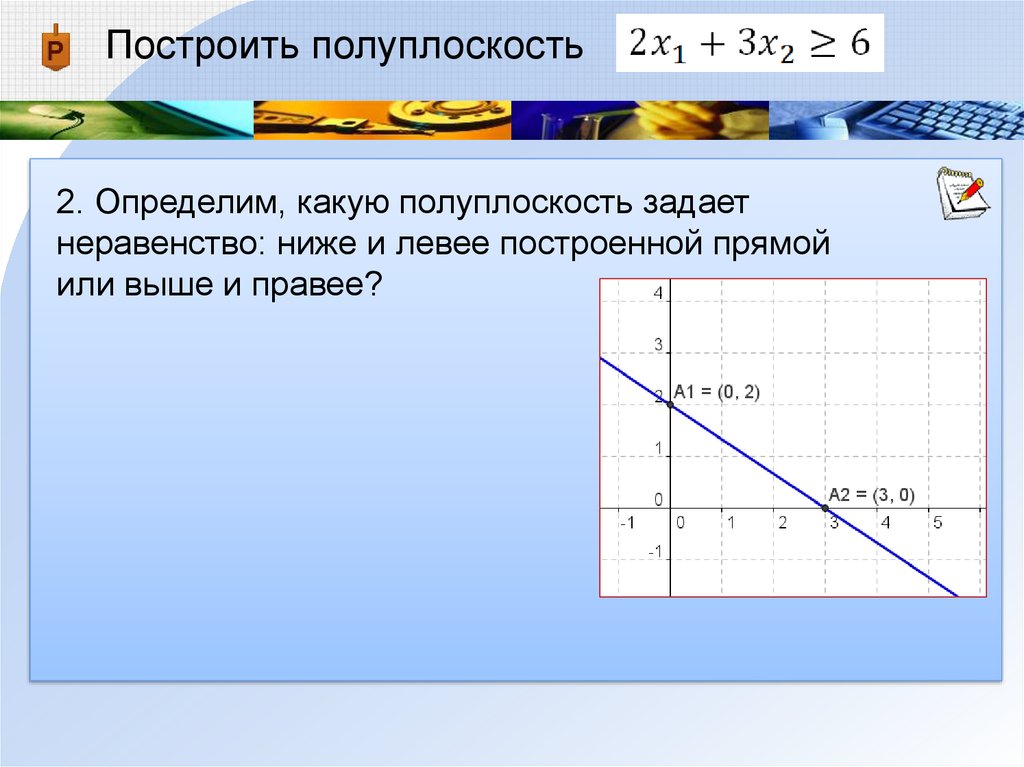
Построить полуплоскость2. Определим, какую полуплоскость задает
неравенство: ниже и левее построенной прямой
или выше и правее?
74.
Построить полуплоскость2. Определим, какую полуплоскость задает
неравенство?
Выбираем произвольную
точку, не лежащую на
прямой, например А(4;1)
Подставляем ее
координаты в
неравенство:
75.
Построить полуплоскость2. Определим, какую полуплоскость задает
неравенство?
Получили верное
числовое неравенство,
значит данное
неравенство задает
полуплоскость
содержащую точку А(4;1),
т.е. выше и правее прямой
76.
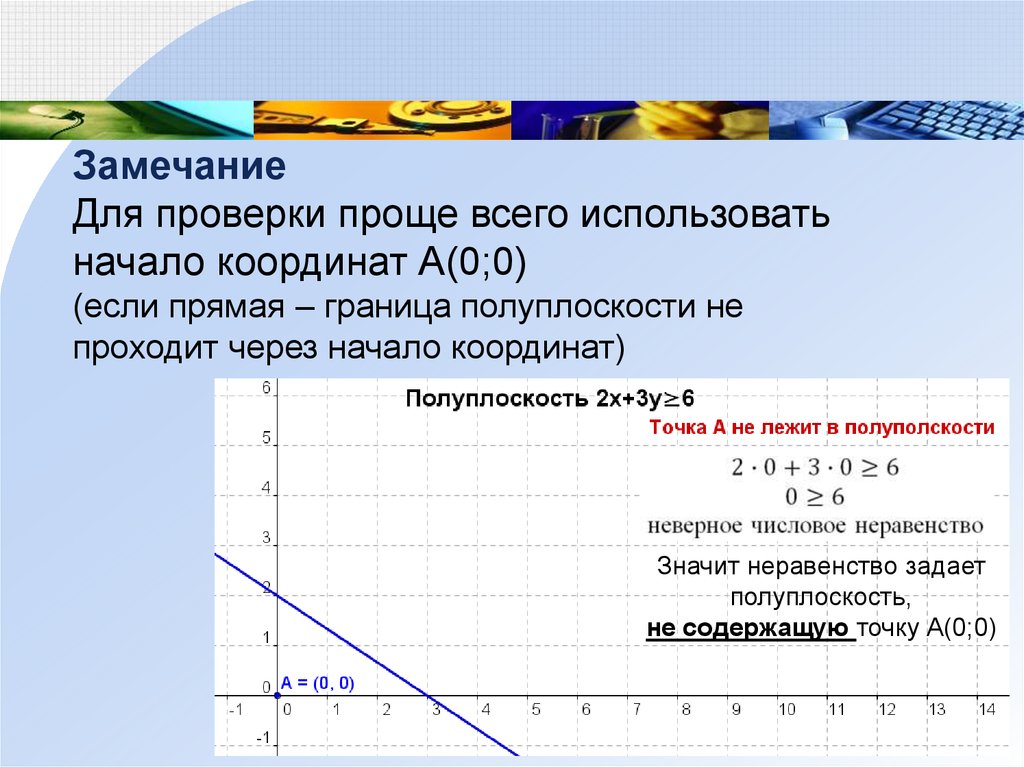
ЗамечаниеДля проверки проще всего использовать
начало координат А(0;0)
(если прямая – граница полуплоскости не
проходит через начало координат)
Значит неравенство задает
полуплоскость,
не содержащую точку А(0;0)
77.
Для построения множества точек,удовлетворяющих системе линейных
неравенств необходимо построить
пересечение полуплоскостей, заданных
всеми неравенствами
78.
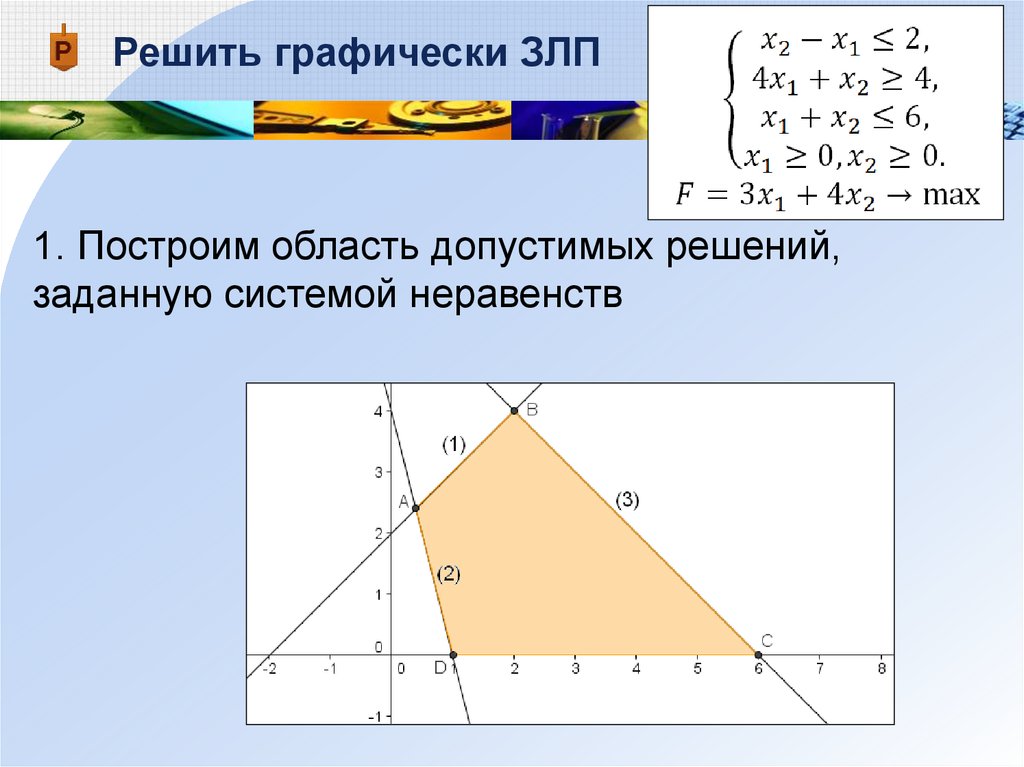
Решить графически ЗЛП79.
Решить графически ЗЛП1. Построим область допустимых решений,
заданную системой неравенств
80.
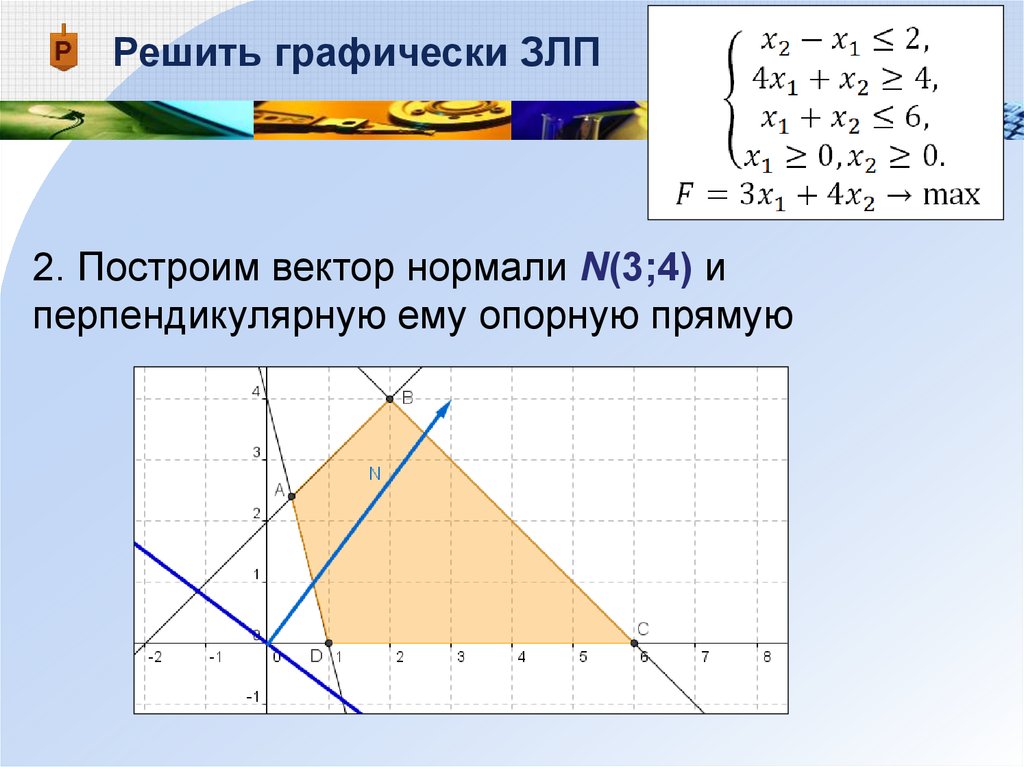
Решить графически ЗЛП2. Построим вектор нормали N(3;4) и
перпендикулярную ему опорную прямую
81.
Решить графически ЗЛП3. Перемещаем опорную прямую в направлении
вектора нормали и определяем «точку выхода»
В – точка выхода
82.
Решить графически ЗЛП4. Найдем координаты точки В, как точки
пересечения прямых (1) и (3)
83.
Решить графически ЗЛП4. Найдем координаты точки В, как точки
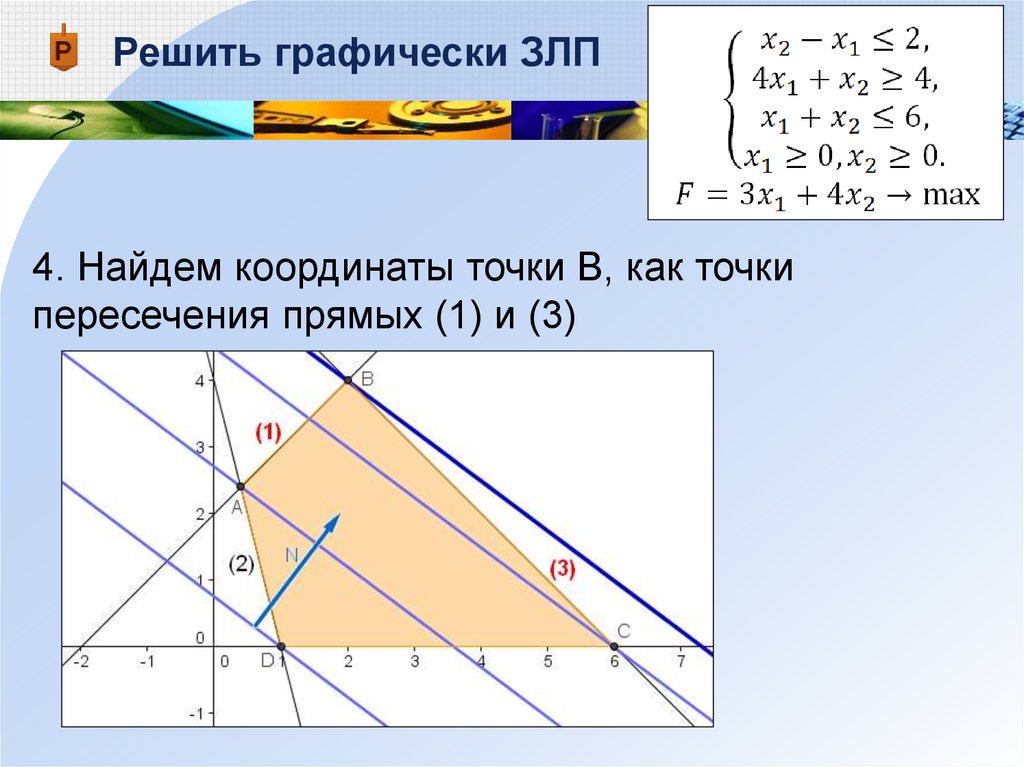
пересечения прямых (1) и (3):
84.
Решить графически ЗЛП5. Найдем значение целевой функции в точке В
85.
Решить графически ЗЛПОтвет:
86.
87.
88.
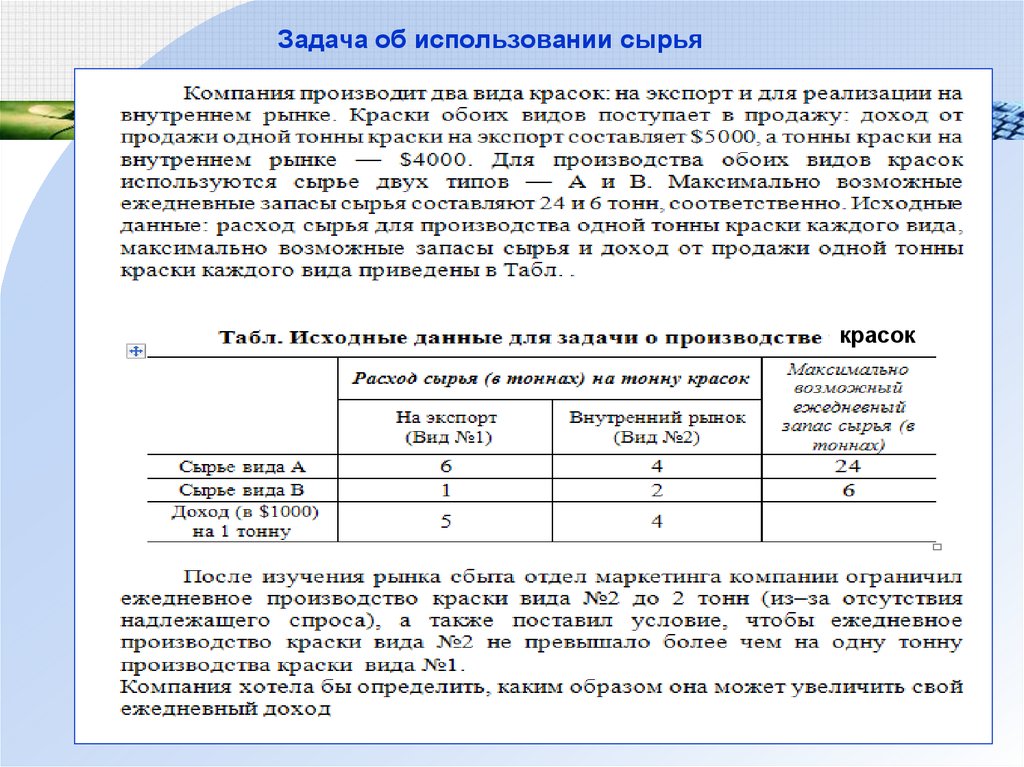
89. Задача об использовании сырья
красок90. Задача об использовании сырья
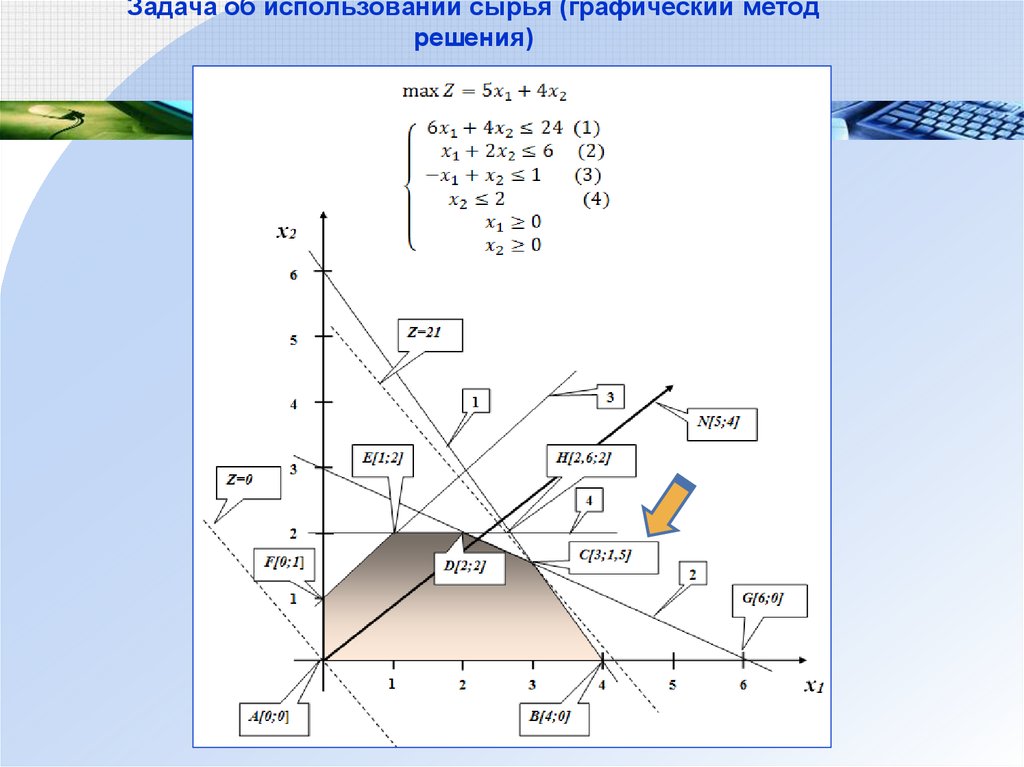
91. Задача об использовании сырья (графический метод решения)
92. Сущность метода
Симплекс-метод – универсальныйметод
решения
задач
линейного
программирования.
Суть
метода:
целенаправленный
перебор решений, соответствующих
вершинам
многогранника
области
допустимых решений.
93. Сущность метода
Метод применим к любой задаче линейногопрограммирования в канонической форме:
F ( x) c1 x1 c2 x2 ... cn xn с max(min)
a11 x1 a12 x2 ...a1n xn b1
a21 x1 a22 x2 ...a2 n xn b2
....
am1 x1 am 2 x2 ...amn xn bm
x j 0, j 1...n
Количество неизвестных (n) в системе
ограничений должно быть больше количества
уравнений (m).
94. Основные этапы решения задачи симплекс-методом
1. Приведение задачи к каноническому виду.2. Приведение
задачи
к
допустимому
виду
(выделение базиса) и преобразование целевой
функции.
3. Нахождение первого допустимого базисного
решения системы ограничений или установление
факта ее несовместности.
4. Проверка
полученного
решения
на
оптимальность. Если решение не оптимально, то
5. Поиск другого допустимого базисного решения,
при котором целевая функция достигает как
минимум не меньшего значения.
П. 4 и 5 повторяются до нахождения оптимального
решения
95. 1. Приведение задачи к каноническому виду
Для приведения задачи к каноническомувиду необходимо добавить в каждое из
ограничений
задачи,
представленных
неравенствами, по одной переменной.
Например:
Неканонический вид:
Канонический
вид:
F ( x) x1 2 x2 max
F ( x) x1 2 x2 max
x1 x2 6
x1 x2 x3 6
x1 2 x2 12
x1 2 x2 x4 12
.x ,x 0
1
2
x1 , x2 0
96. 2. Приведение задачи к допустимому виду
Для того, чтобы привести системууравнений
к
допустимому
виду,
необходимо
выразить
любые
m
неизвестных через остальные:
x1 a1m 1 xm 1 ...a1n xn b1
x2 a2 m 1 xm 1 ...a2 n xn b2
....
xm amm 1 xm 1 ...amn xn bm
bi ≥ 0
97. 2. Приведение задачи к допустимому виду
Неизвестные,которые
выражаются
через
остальные
неизвестные,
называются базисными, а весь набор
этих неизвестных – базисом.
Остальные неизвестные называются
свободными.
Количество
базисных
переменных
должно
равняться
количеству
уравнений в системе.
98. 2. Преобразование целевой функции
Далее необходимо преобразоватьцелевую функцию, исключив из нее
базисные переменные.
Для исключения базисных переменных
из целевой функции нужно умножить
первое уравнение системы ограничений
на c1, второе на c2, и т.д., сложить
полученные произведения и вычесть
целевую функцию.
99. 2. Преобразование целевой функции
Получим:m 1 xm 1 ... n xn F0 F
или
где
F F0 m 1 xm 1 ... n xn
m
F0 ci bi
i 1
m
j c1a1 j c2 a2 j ... cm amj c j ci aij c j
i 1
100. 3. Нахождение первого допустимого базисного решения
Приравняем свободные переменные кнулю и найдем значения базисных
переменных.
Получим
одно
из
базисных
решений
системы
ограничений.
Базисное
решение
называется
допустимым базисным решением или
опорным решением, если значения
базисных
переменных
в
нем
неотрицательны.
101. 3. Основная теорема симплекс-метода
Среди оптимальных планов задачилинейного
программирования
в
канонической форме обязательно есть
опорное
решение
ее
системы
ограничений.
Таким
образом
симплекс-метод
представ-ляет
собой
процедуру
направленного
перебора
опорных
решений.
102. 4. Проверка решения на оптимальность
Допустимое базисное решение системыограничений является оптимальным
решением
задачи
линейного
программирования тогда и только тогда,
когда все ∆j ≥ 0.
Если все ∆j строго положительны, то
решение является единственным.
103. 5. Поиск другого допустимого базисного решения
Если полученное допустимое базисноерешение системы ограничений не
является оптимальным, необходимо
найти другое допустимое базисное
решение, при котором целевая функция
достигает как минимум не меньшего
значения.
104. Основные этапы решения задачи симплекс-методом
1. Приведение задачи к каноническому виду.2. Приведение
задачи
к
допустимому
виду
(выделение базиса) и преобразование целевой
функции.
3. Нахождение первого допустимого базисного
решения системы ограничений или установление
факта ее несовместности.
4. Проверка
полученного
решения
на
оптимальность. Если решение не оптимально, то
5. Поиск другого допустимого базисного решения,
при котором целевая функция достигает как
минимум не меньшего значения.
П. 4 и 5 повторяются до нахождения оптимального
решения
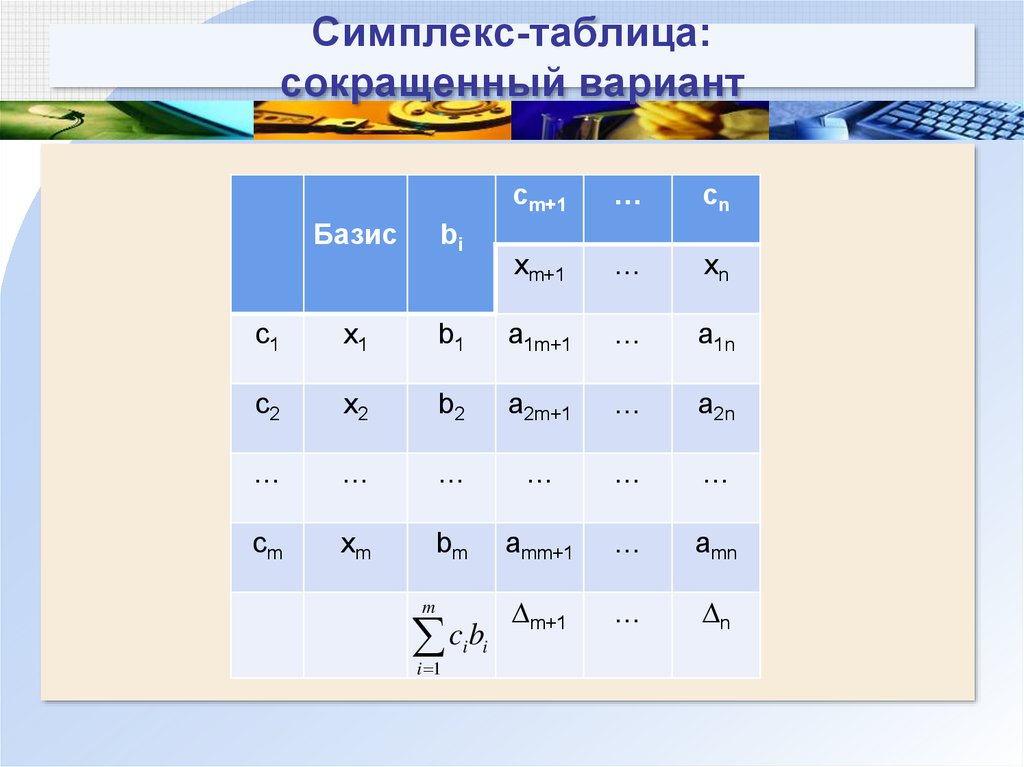
105. Симплекс-таблица
Пусть задача приведена к виду:m 1 xm 1 ... n xn F0 F
x1 a1m 1 xm 1 ...a1n xn b1
x2 a2 m 1 xm 1 ...a2 n xn b2
....
xm amm 1 xm 1 ...amn xn bm
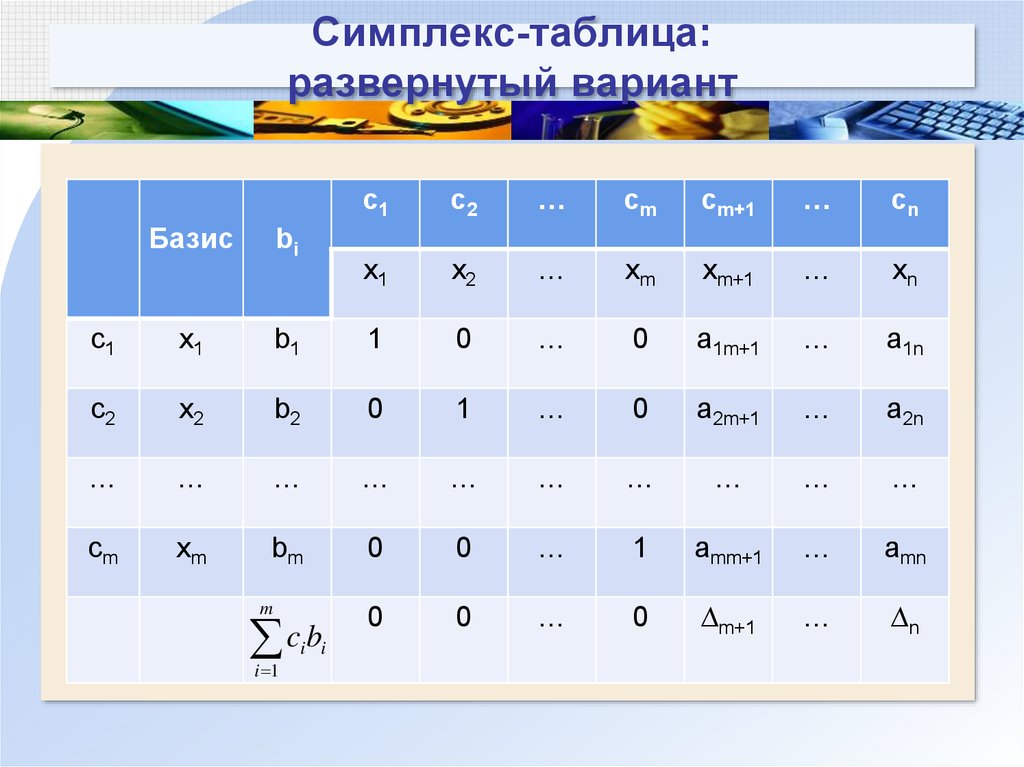
106. Симплекс-таблица: развернутый вариант
Базисbi
c1
c2
…
cm
cm+1
…
cn
x1
x2
…
xm
xm+1
…
xn
c1
x1
b1
1
0
…
0
a1m+1
…
a1n
c2
x2
b2
0
1
…
0
a2m+1
…
a2n
…
…
…
…
…
…
…
…
…
…
cm
xm
bm
0
0
…
1
amm+1
…
amn
0
0
…
0
∆m+1
…
∆n
m
cibi
i 1
107. Симплекс-таблица: сокращенный вариант
Базисbi
cm+1
…
cn
xm+1
…
xn
c1
x1
b1
a1m+1
…
a1n
c2
x2
b2
a2m+1
…
a2n
…
…
…
…
…
…
cm
xm
bm
amm+1
…
amn
c b
∆m+1
…
∆n
m
i 1
i i
108. Симплекс-таблица: алгоритм решения
1. Просматривается последняя строкатаблицы, среди коэффициентов этой
строки (исключая столбец свободных
членов)
выбирается
наименьшее
отрицательное число. Если такового
нет, то исходное базисное решение
является оптимальным.
109. Симплекс-таблица: алгоритм решения
2. Столбец таблицы, соответствующийвыбранному
отрицательному
коэффици-енту в последней строке
называется ключевым. В этом столбце
выбираются
положительные
коэффициенты. Если таковых нет, то
задача решений не имеет.
110. Симплекс-таблица: алгоритм решения
3. Среди положительных коэффициентовключевого столбца выбирается тот, для
которого абсолютная величина отношения
соответствующего свободного члена к
этому
элементу
минимальна.
Этот
коэффициент называется разрешающим
или ключевым, а строка, в которой он
находится, ключевой.
111. Симплекс-таблица: алгоритм решения
4. Базисная переменная, отвечающаястроке ключевого элемента, должна
быть переведена в разряд свободных, а
свободная переменная, отвечающая
столбцу ключевого элемента, вводится
в число базисных. Новая таблица
строится по следующему алгоритму.
112. Симплекс-таблица: алгоритм решения
4а) в обозначениях строк и столбцов переменная,вводимая в базис и переменная, выводимая из
него, меняются местами;
4б) на месте ключевого элемента записываем
обратное ему число;
4в) ключевую строку (за исключением ключевого
элемента)
делим
на
ключевой
элемент;
полученную строку вписываем на место ключевой;
4г) ключевой столбец (за исключением ключевого
элемента) делим на ключевой элемент с
противоположным знаком; полученный столбец
вписываем на место ключевого;
113. Симплекс-таблица: алгоритм решения
4д) все остальные элементы таблицы,включая строку оценок и столбец
свободных членов, пересчитываем по так
называемому «правилу прямоугольника»:
на основе пересчитываемой клетки и
клетки с ключевым элементом мысленно
составляем
прямоугольник,
далее
перемножаем элементы, стоящие в двух
оставшихся его вершинах, полученное
произведение делим на ключевой элемент
и
вычитаем
из
пересчитываемого
элемента.
114. Симплекс-таблица: алгоритм решения
5. Новая симплекс-таблица отвечаетновому
допустимому
базисному
решению. Проверяем новое решение на
оптимальность, если решение не
оптимально, то повторяем алгоритм.
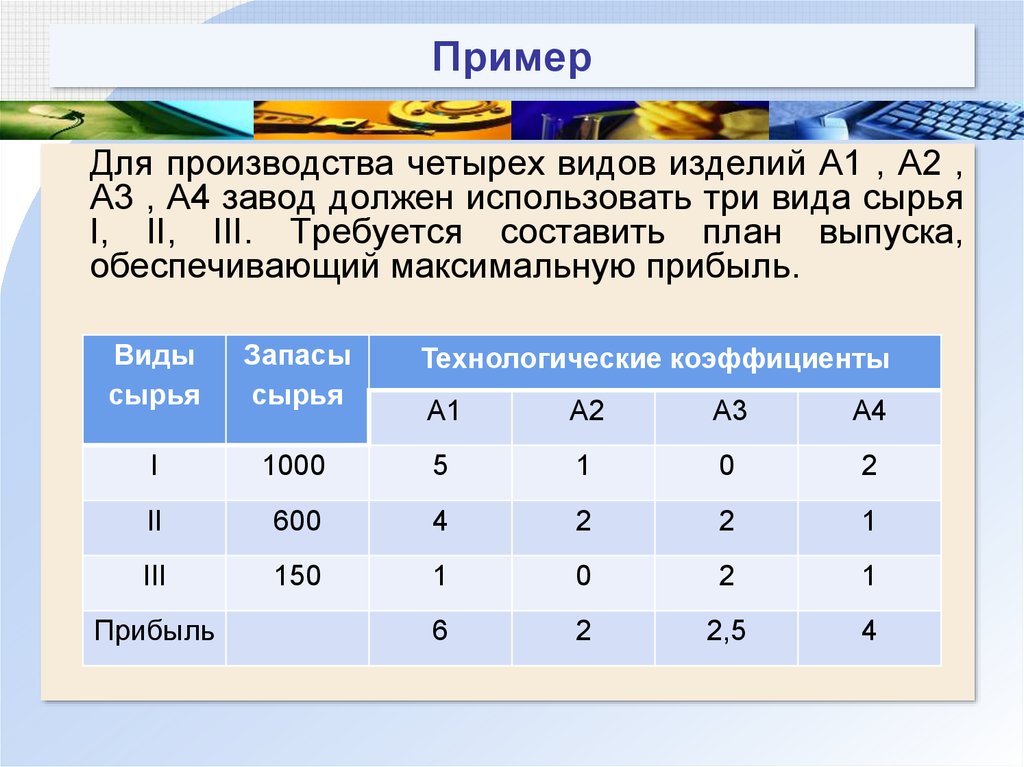
115. Пример
Для производства четырех видов изделий A1 , A2 ,A3 , A4 завод должен использовать три вида сырья
I, II, III. Требуется составить план выпуска,
обеспечивающий максимальную прибыль.
.
Виды
сырья
Запасы
сырья
I
Технологические коэффициенты
A1
A2
A3
A4
1000
5
1
0
2
II
600
4
2
2
1
III
150
1
0
2
1
6
2
2,5
4
Прибыль
116. Пример
Математическая модель задачи:F ( x) 6 x1 2 x2 2,5 x3 4 x4 max
5 x1 x2 2 x4 1000
4 x1 2 x2 2 x3 x4 600
x1 2 x3 x4 150
x j 0, j 1,2,3,4
.
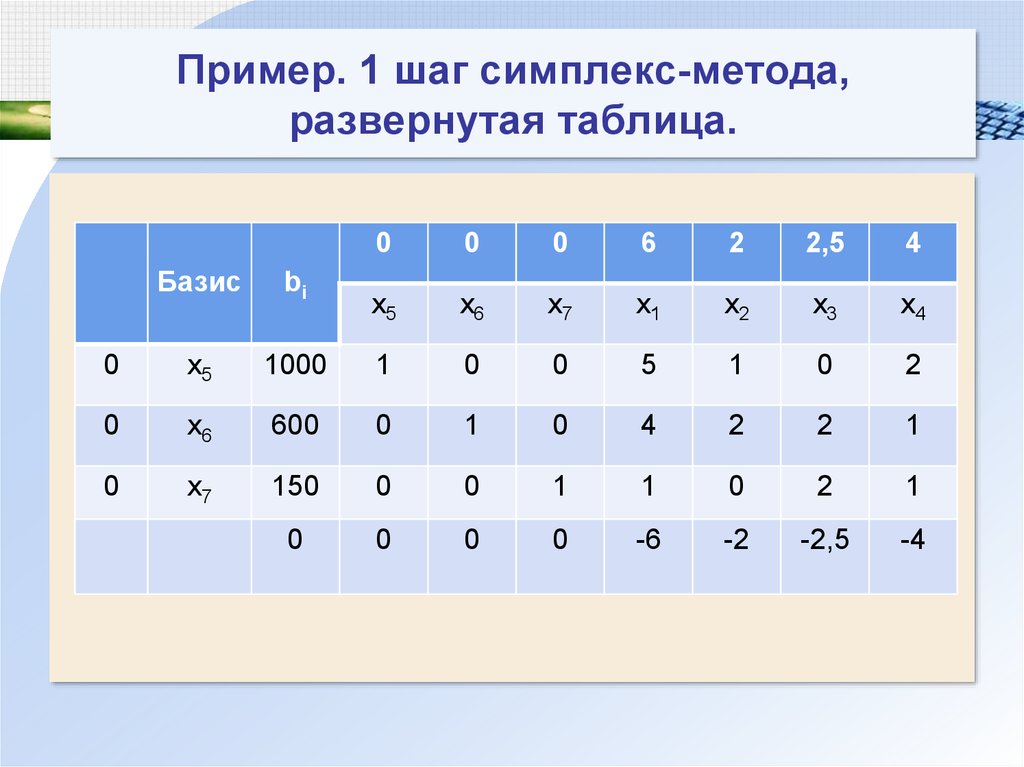
117. Пример
Приведение задачи к каноническому виду:F ( x) 6 x1 2 x2 2,5 x3 4 x4 max
5 x1 x2 2 x4 x5 1000
4 x1 2 x2 2 x3 x4 x6 600
x1 2 x3 x4 x7 150
x j 0, j 1,2,3,4,5,6,7
Примем за базисные переменные x5, x6, x7.
Тогда первое опорное решение:
(0; 0; 0; 0; 1000; 600; 150).
118. Пример. 1 шаг симплекс-метода, развернутая таблица.
00
0
6
2
2,5
4
x5
x6
x7
x1
x2
x3
x4
Базис
bi
0
x5
1000
1
0
0
5
1
0
2
0
x6
600
0
1
0
4
2
2
1
0
x7
150
0
0
1
1
0
2
1
0
0
0
0
-6
-2
-2,5
-4
119. Пример. 1 шаг симплекс-метода, сокращенная таблица.
62
2,5
4
x1
x2
x3
x4
Базис
bi
0
x5
1000
5
1
0
2
0
x6
600
4
2
2
1
0
x7
150
1
0
2
1
0
-6
-2
-2,5
-4
120. Пример. 1 шаг симплекс-метода
Базисное решение (0; 0; 0; 0; 1000; 600;150).
Поиск ключевой строки:
1000 600 150
min{
;
;
} 150
5
4
1
Выводим из базиса переменную x7 и
вводим переменную x1
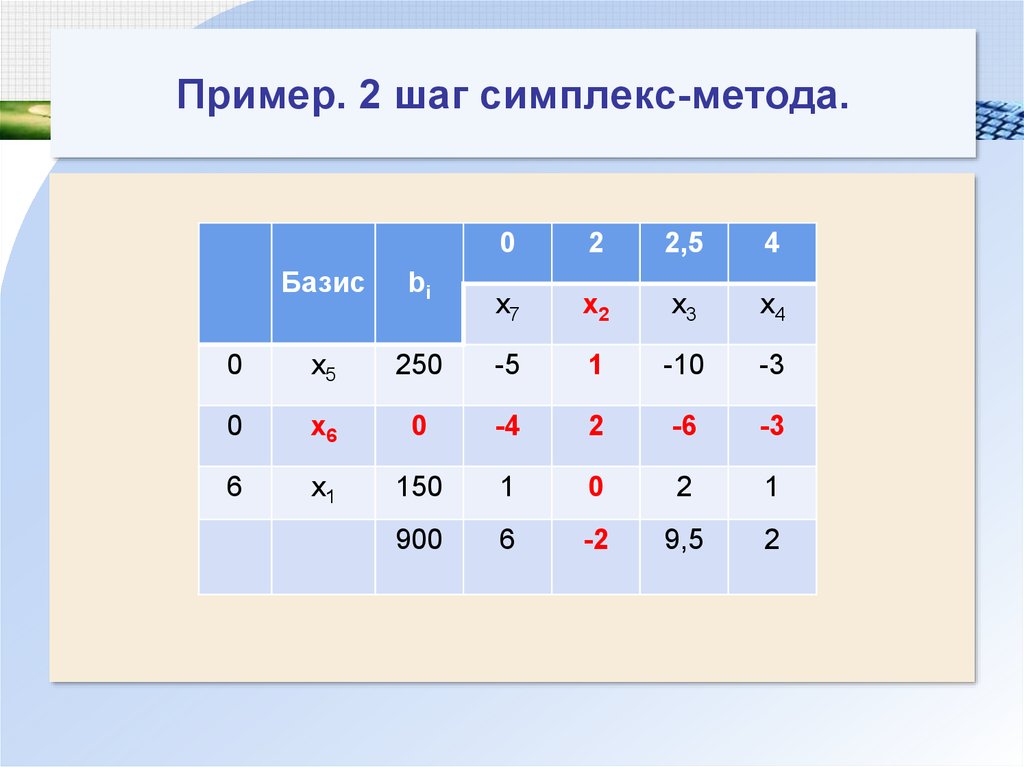
121. Пример. 2 шаг симплекс-метода.
02
2,5
4
x7
x2
x3
x4
Базис
bi
0
x5
250
-5
1
-10
-3
0
x6
0
-4
2
-6
-3
6
x1
150
1
0
2
1
900
6
-2
9,5
2
122. Пример. 2 шаг симплекс-метода
Базисное решение (150; 0; 0; 0; 250; 0; 0).Определение ключевой строки:
0 250
min{ ;
} 0
2 1
Выводим из базиса переменную x6 и
вводим переменную x2.
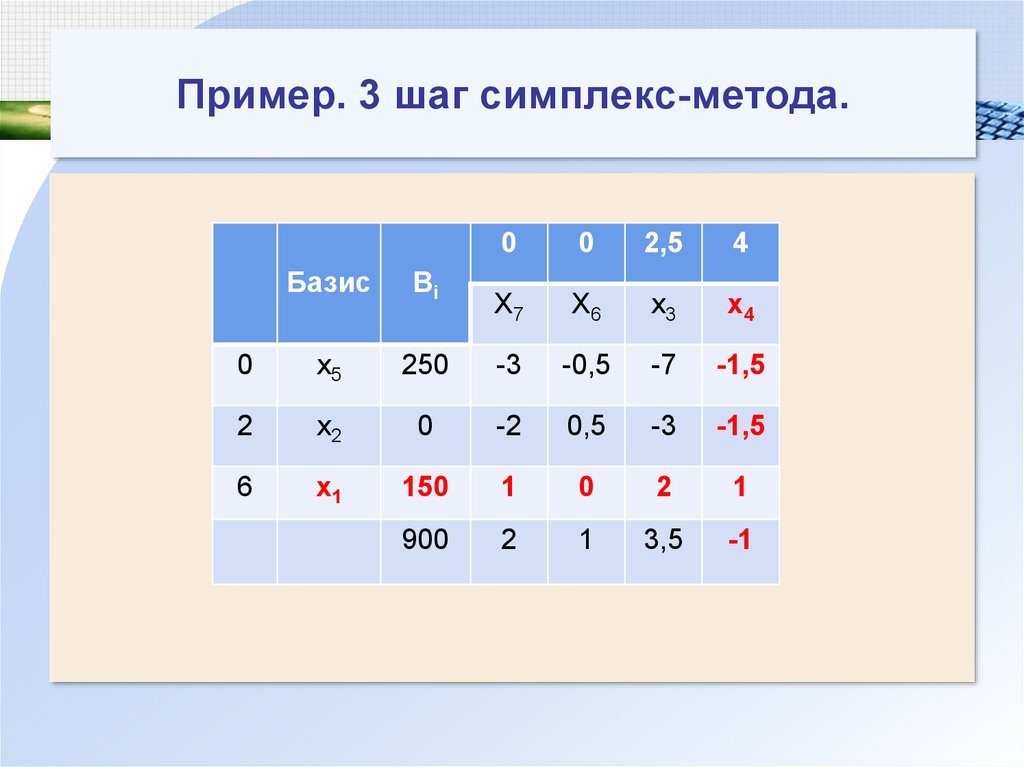
123. Пример. 3 шаг симплекс-метода.
00
2,5
4
X7
X6
x3
x4
Базис
Bi
0
x5
250
-3
-0,5
-7
-1,5
2
x2
0
-2
0,5
-3
-1,5
6
x1
150
1
0
2
1
900
2
1
3,5
-1
124. Пример. 3 шаг симплекс-метода
Базисное решение (150; 0; 0; 0; 250; 0; 0).Определение ключевой строки:
150
min{ } 150
1
Выводим из базиса переменную x1 и
вводим переменную x4.
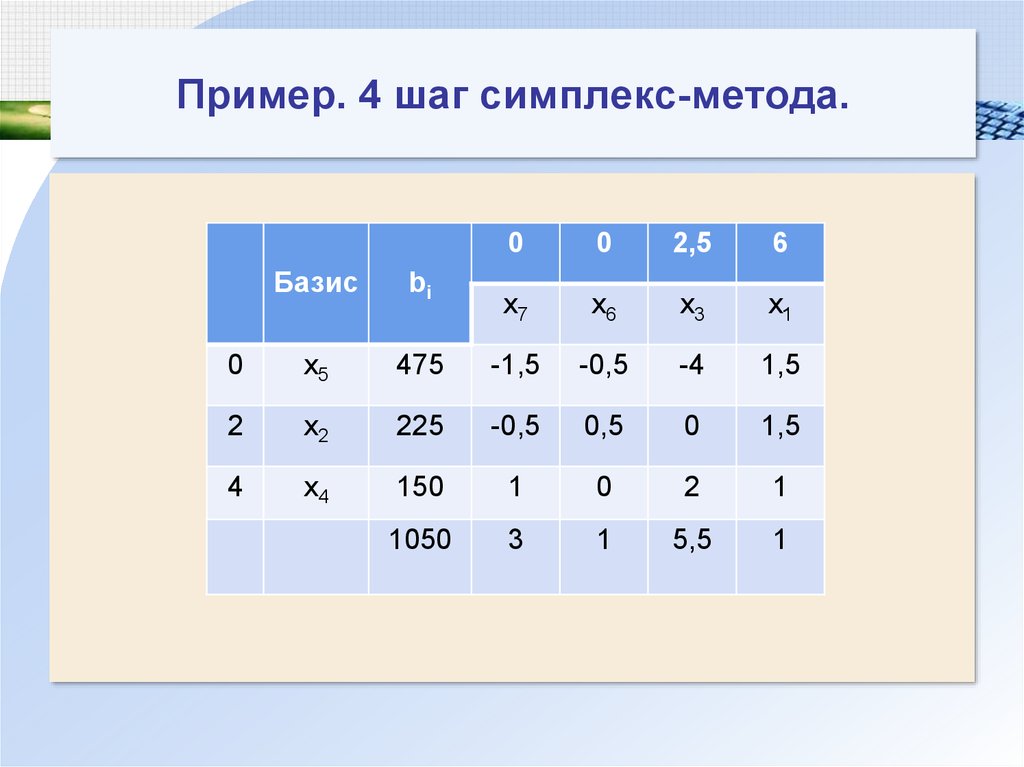
125. Пример. 4 шаг симплекс-метода.
00
2,5
6
x7
x6
x3
x1
Базис
bi
0
x5
475
-1,5
-0,5
-4
1,5
2
x2
225
-0,5
0,5
0
1,5
4
x4
150
1
0
2
1
1050
3
1
5,5
1
126. Пример. 4 шаг симплекс-метода
Оптимальное решение:(0; 225; 0; 150; 475; 0; 0),
при котором Fmax = 1050.
То есть, для получения наибольшей
прибыли, равной 1050 денежных единиц,
предприятие должно выпустить 225
единиц продукции вида A2, 150 единиц
продукции вида A4. Продукцию вида A1 и
A3 производить не выгодно. При этом
сырье типа II и III будет использовано
полностью, а 475 единиц сырья типа I
останутся неизрасходованными.
127.
Транспортная задача128.
129. Решение транспортной задачи
Решение транспортной задачи разбивается на два этапа:а) определение исходного опорного решения;
б) построение последовательных итераций, т.е. приближение к
оптимальному решению.
Решение считается оптимальным, если найденная
неотрицательная матрица X удовлетворяет условиям
Теорема: для разрешимости
транспортной задачи необходимо
и достаточно, чтобы выполнялось
условие баланса:
130.
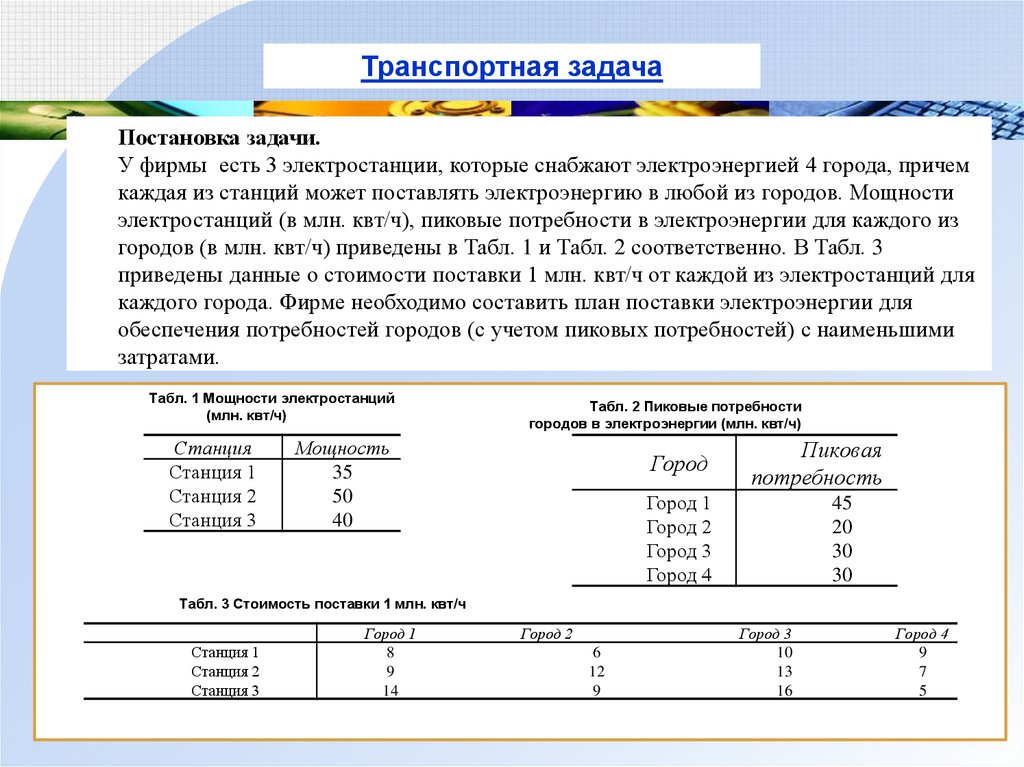
Транспортная задачаПостановка задачи.
У фирмы есть 3 электростанции, которые снабжают электроэнергией 4 города, причем
каждая из станций может поставлять электроэнергию в любой из городов. Мощности
электростанций (в млн. квт/ч), пиковые потребности в электроэнергии для каждого из
городов (в млн. квт/ч) приведены в Табл. 1 и Табл. 2 соответственно. В Табл. 3
приведены данные о стоимости поставки 1 млн. квт/ч от каждой из электростанций для
каждого города. Фирме необходимо составить план поставки электроэнергии для
обеспечения потребностей городов (с учетом пиковых потребностей) с наименьшими
затратами.
Табл. 1 Мощности электростанций
(млн. квт/ч)
Станция
Станция 1
Станция 2
Станция 3
Табл. 2 Пиковые потребности
городов в электроэнергии (млн. квт/ч)
Мощность
35
50
40
Город
Пиковая
потребность
Город 1
Город 2
Город 3
Город 4
45
20
30
30
Табл. 3 Стоимость поставки 1 млн. квт/ч
Станция 1
Станция 2
Станция 3
Город 1
8
9
14
Город 2
6
12
9
Город 3
10
13
16
Город 4
9
7
5
131.
План решения транспортной задачи=СУММПРОИЗВ(C6:F8;C13:F15)
=СУММ(C13:F13)
=СУММ(F13:F16)
132.
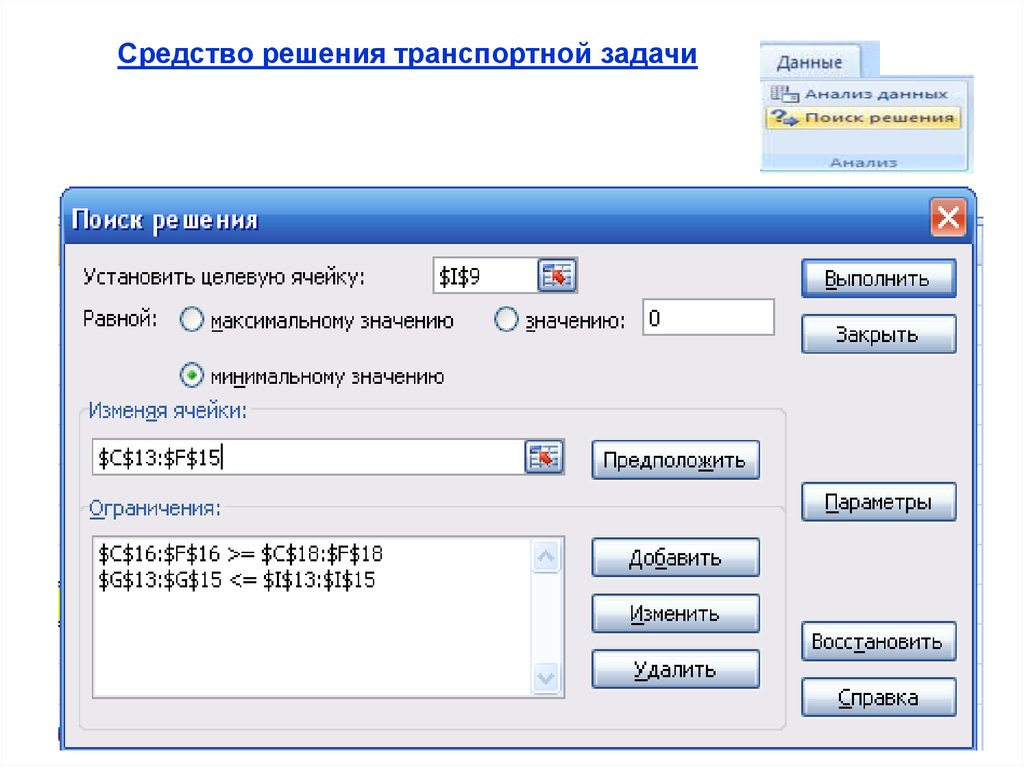
Средство решения транспортной задачи133.
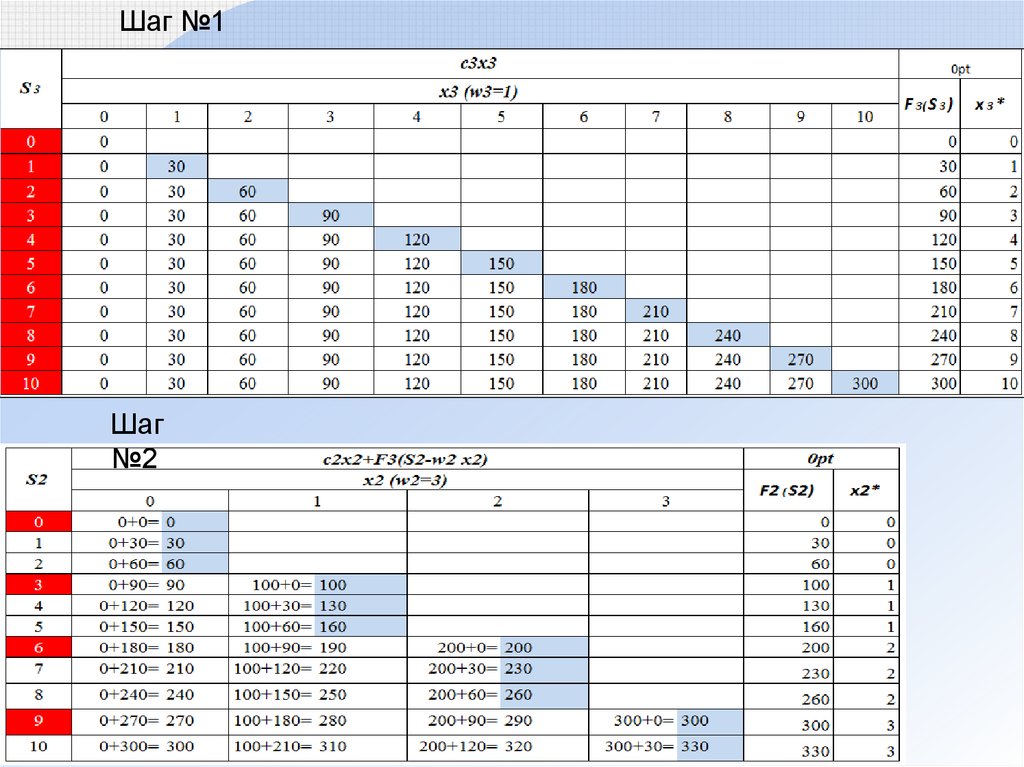
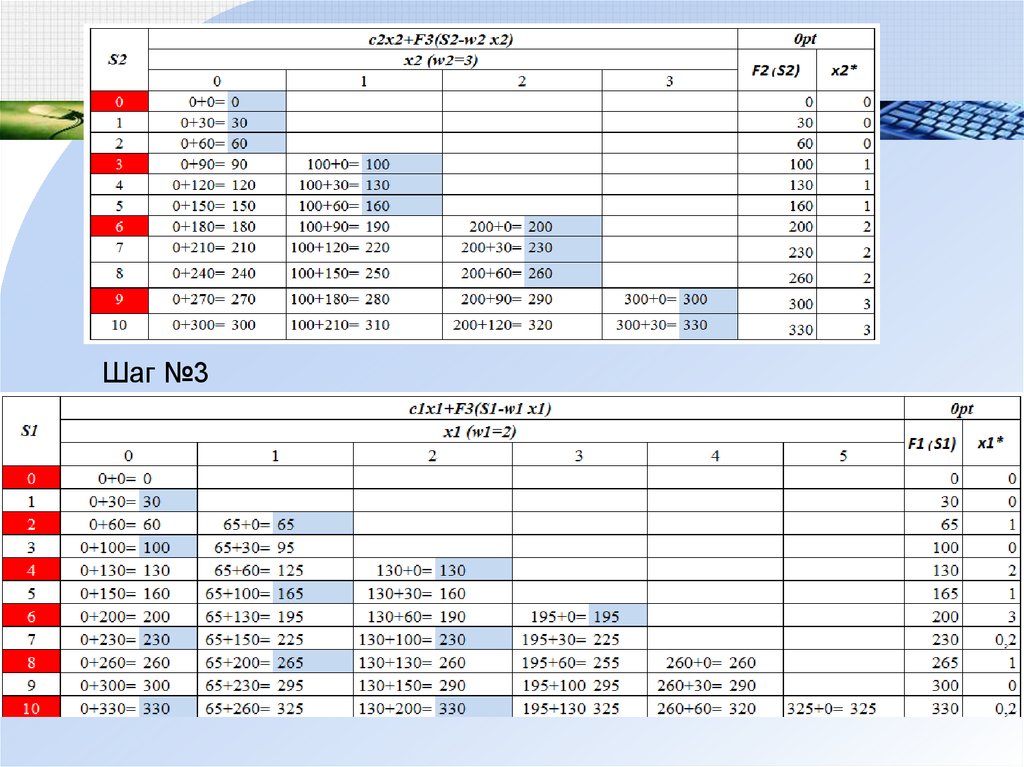
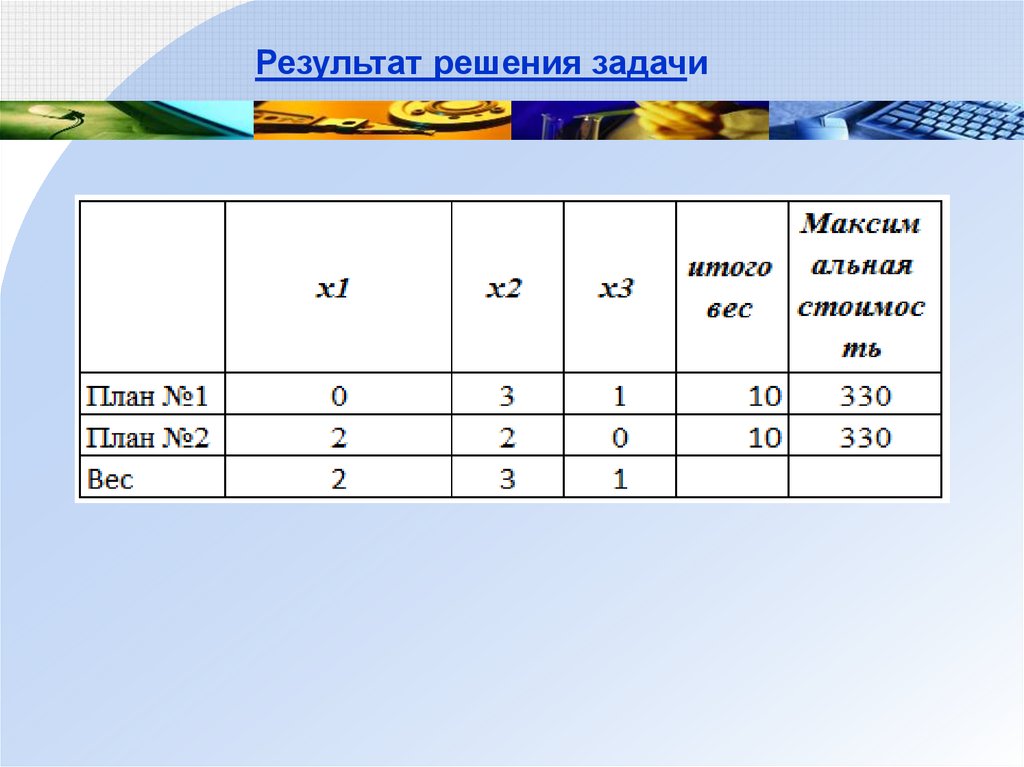
2. Задача о рюкзаке (динамическое программирование)Постановка задачи
Самолет загружается предметами N различных типов с весом wj и
стоимостью cj. Максимальная грузоподъемность равна W = 10 тонн. Определить
план загрузки, максимальную стоимость груза, вес которого не более W = 10 тонн.
134.
Шаг №1Шаг
№2
































































































 Математика
Математика








