Похожие презентации:
Введение в биомедицинскую статистику
1.
ВВЕДЕНИЕВ БИОМЕДИЦИНСКУЮ СТАТИСТИКУ
МОРДОВСКИЙ ЭДГАР АРТУРОВИЧ
К.М.Н., ДОЦЕНТ
1
2. ПЛАН
• Биомедицинская статистика: назначение, задачи• Статистическое исследование
• Типы переменных в статистике
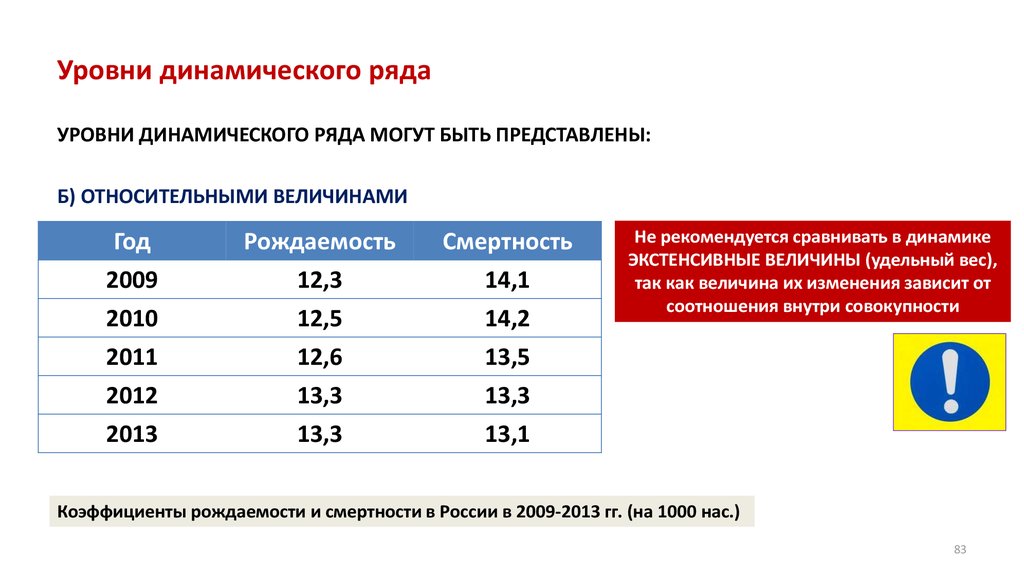
• Относительные величины в медицинской статистике
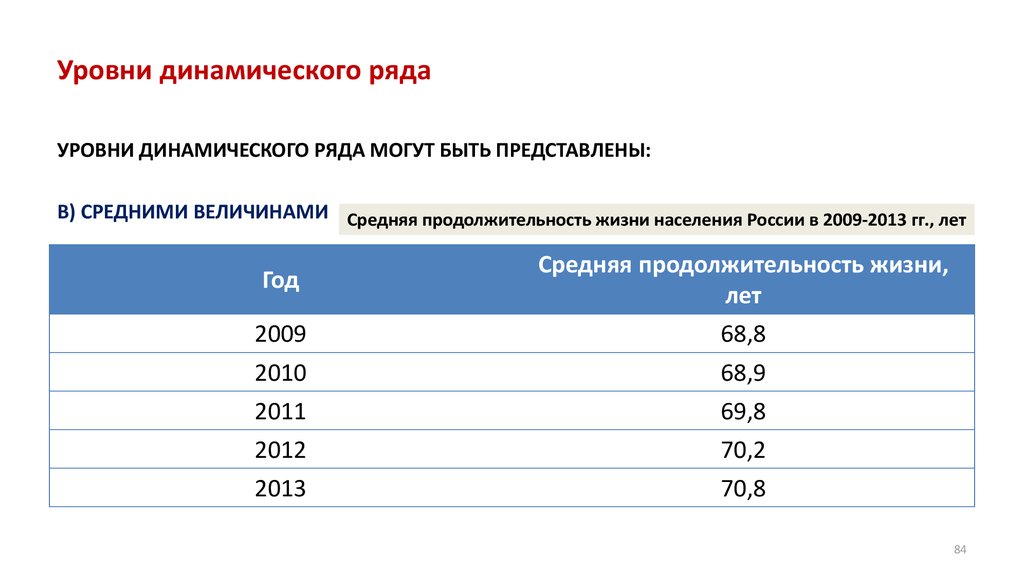
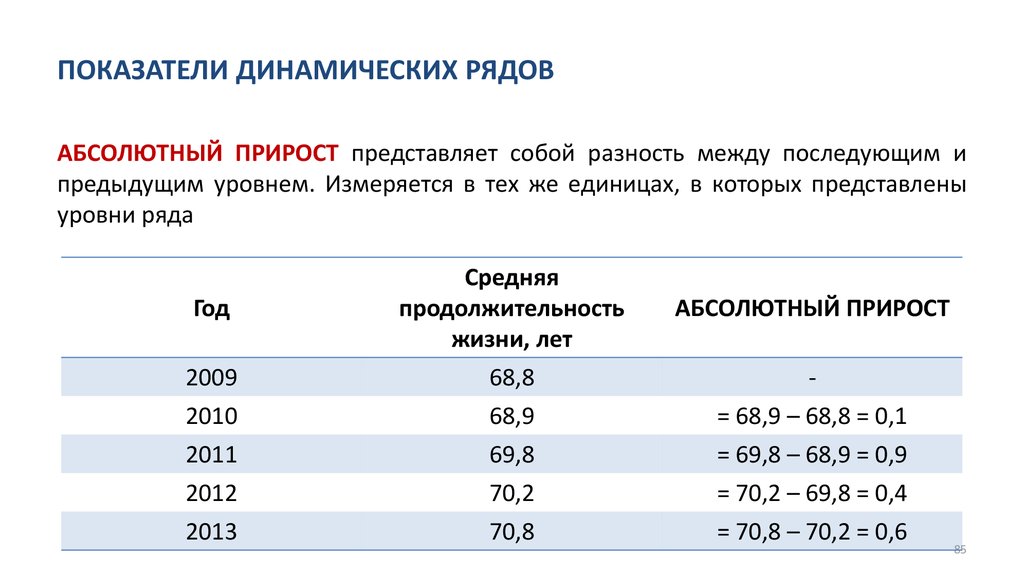
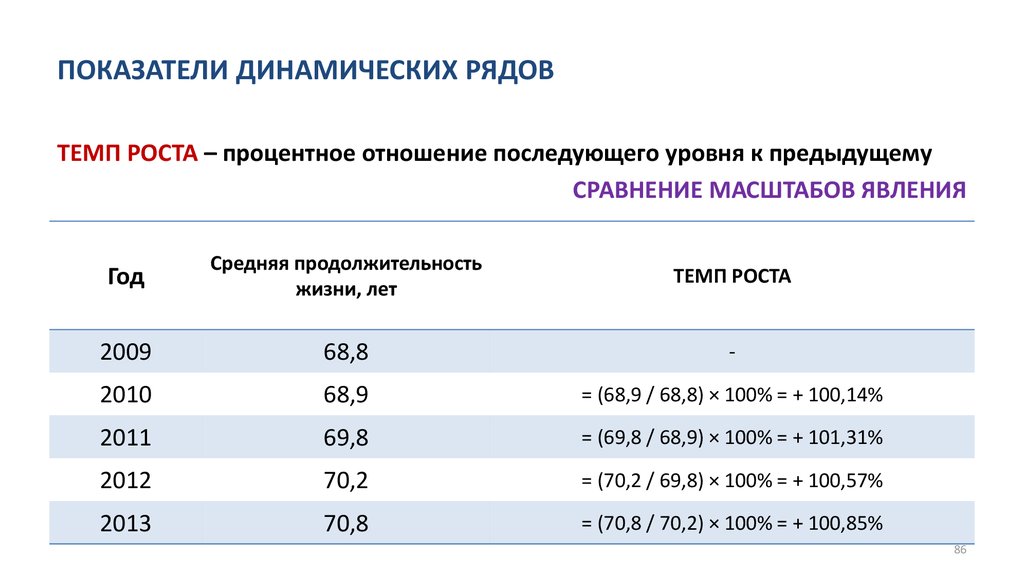
• Анализ динамических рядов
3. Медицинская статистика: Назначение, Задачи
МЕДИЦИНСКАЯ СТАТИСТИКА: НАЗНАЧЕНИЕ, ЗАДАЧИ3
4. СТАТИСТИКА
отрасль знаний, в которой излагаются общие вопросы сбора, измерения ианализа массовых статистических (количественных или качественных) данных
«СТАТИСТИКА» (от лат. «status» - состояние, положение)
Впервые термин применил Готфрид Ахенвалль (сер. XVIII в.)
при описании состояния государства
(нем. statistik, от итал. stato - государство)
4
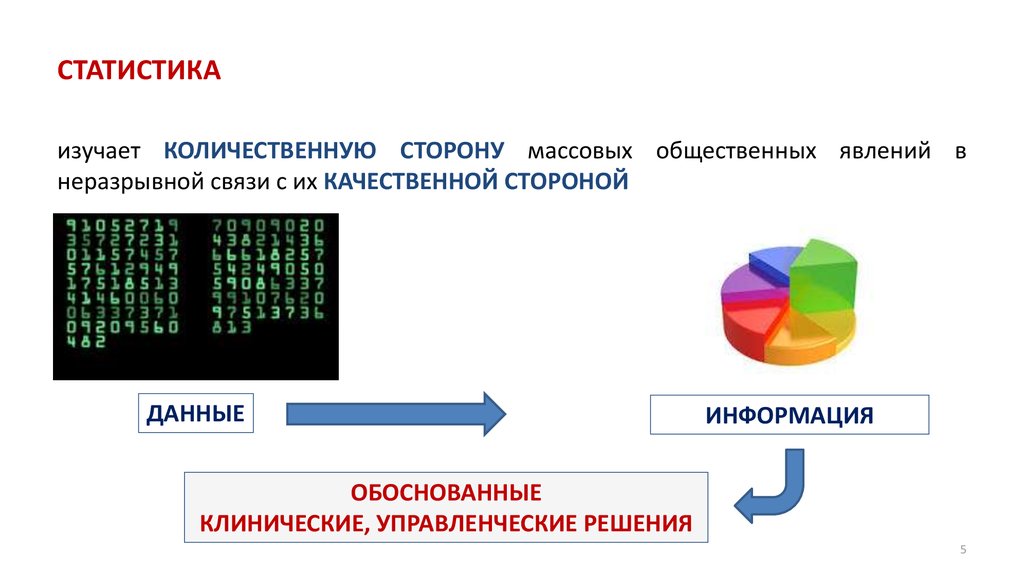
5. СТАТИСТИКА
изучает КОЛИЧЕСТВЕННУЮ СТОРОНУ массовых общественных явлений внеразрывной связи с их КАЧЕСТВЕННОЙ СТОРОНОЙ
ДАННЫЕ
ИНФОРМАЦИЯ
ОБОСНОВАННЫЕ
КЛИНИЧЕСКИЕ, УПРАВЛЕНЧЕСКИЕ РЕШЕНИЯ
5
6. Закон больших чисел
ЗАКОН БОЛЬШИХ ЧИСЕЛ: количественные закономерности массовых явленийотчетливо проявляются лишь на достаточно большом числе единиц наблюдения
Сущность его заключается в том, что в числах, получающихся в результате
массового наблюдения, выступают определенные закономерности, которые не
могут быть обнаружены в небольшом числе фактов
2 следствия
6
7. Закон больших чисел
следствие 1ЭКОЛОГИЧЕСКАЯ ОШИБКА (ecological fallacy) – результаты, полученные на
выборке, нельзя экстраполировать на единицу наблюдения
Закономерности, обнаруженные на выборке, не могут являться императивом
действий с конкретным человеком (пациентом)
АТОМИСТИЧЕСКАЯ ОШИБКА (atomistic fallacy) – данные, полученные на единице
наблюдения, нельзя экстраполировать на выборку
Мнение одного эксперта не должно быть императивом действий на выборке
7
8. Закон больших чисел
следствие 2Манипулируйте единицами наблюдения и получайте КАКИЕ УГОДНО результаты
«…цифры обманчивы, особенно когда я сам ими занимаюсь; по этому
поводу справедливо высказывание, приписываемое Дизраэли:
«существует три вида лжи: ложь, наглая ложь и статистика».
Марк Твен, 5 июля 1907 г.
8
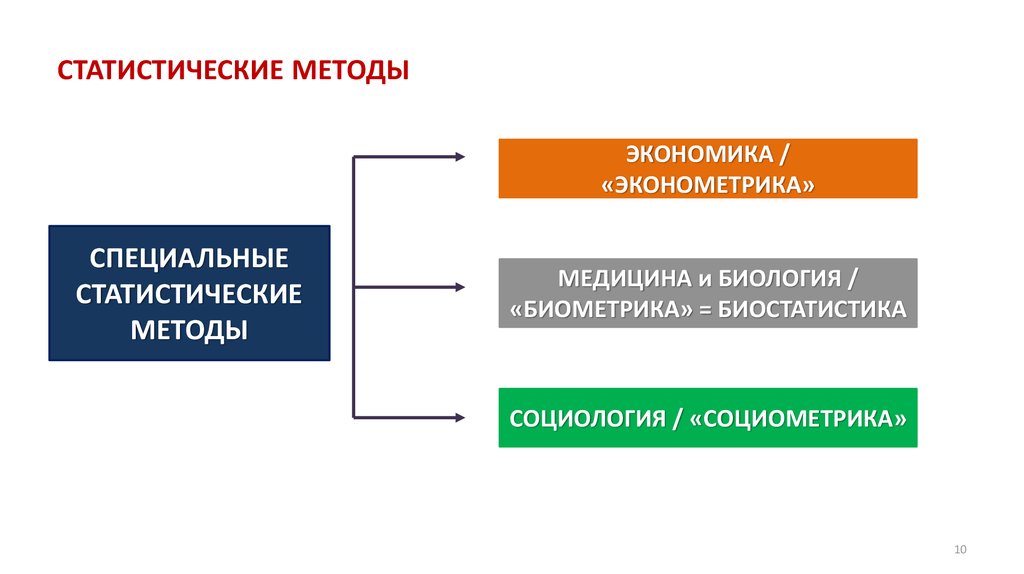
9. СТАТИСТИЧЕСКИЕ МЕТОДЫ
Статистические методы - методы анализа статистических данныхметоды прикладной
статистики
применяются во всех областях
научных исследований
и любых отраслях экономики
и управления
специальные методы
статистики
применяются в отдельных областях
научных исследований
+
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
9
10. СТАТИСТИЧЕСКИЕ МЕТОДЫ
ЭКОНОМИКА /«ЭКОНОМЕТРИКА»
СПЕЦИАЛЬНЫЕ
СТАТИСТИЧЕСКИЕ
МЕТОДЫ
МЕДИЦИНА и БИОЛОГИЯ /
«БИОМЕТРИКА» = БИОСТАТИСТИКА
СОЦИОЛОГИЯ / «СОЦИОМЕТРИКА»
10
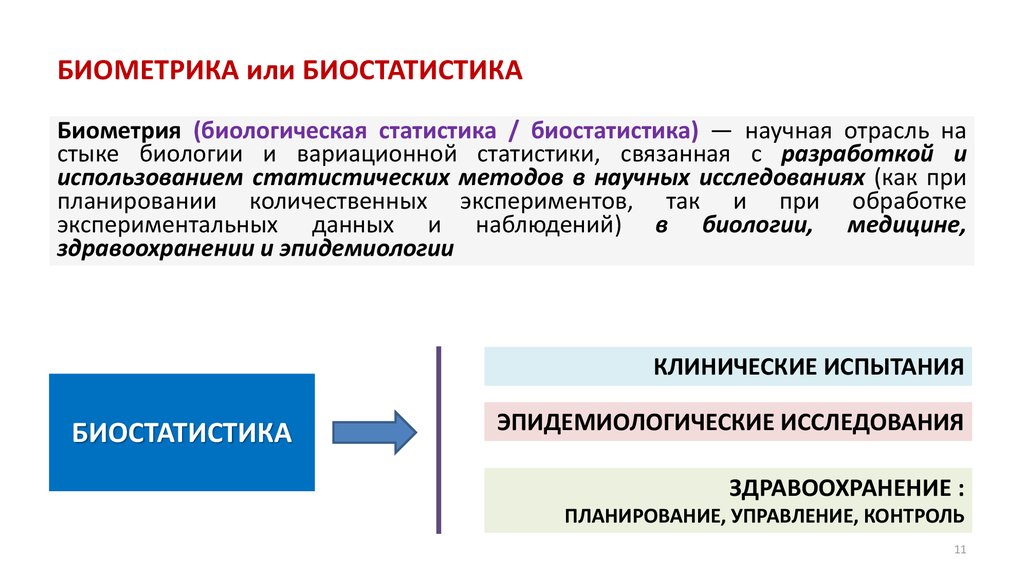
11. БИОМЕТРИКА или БИОСТАТИСТИКА
Биометрия (биологическая статистика / биостатистика) — научная отрасль настыке биологии и вариационной статистики, связанная с разработкой и
использованием статистических методов в научных исследованиях (как при
планировании количественных экспериментов, так и при обработке
экспериментальных данных и наблюдений) в биологии, медицине,
здравоохранении и эпидемиологии
КЛИНИЧЕСКИЕ ИСПЫТАНИЯ
БИОСТАТИСТИКА
ЭПИДЕМИОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ
ЗДРАВООХРАНЕНИЕ :
ПЛАНИРОВАНИЕ, УПРАВЛЕНИЕ, КОНТРОЛЬ
11
12. ИНФОРМАЦИОННАЯ БАЗА СИСТЕМЫ ЗДРАВООХРАНЕНИЯ
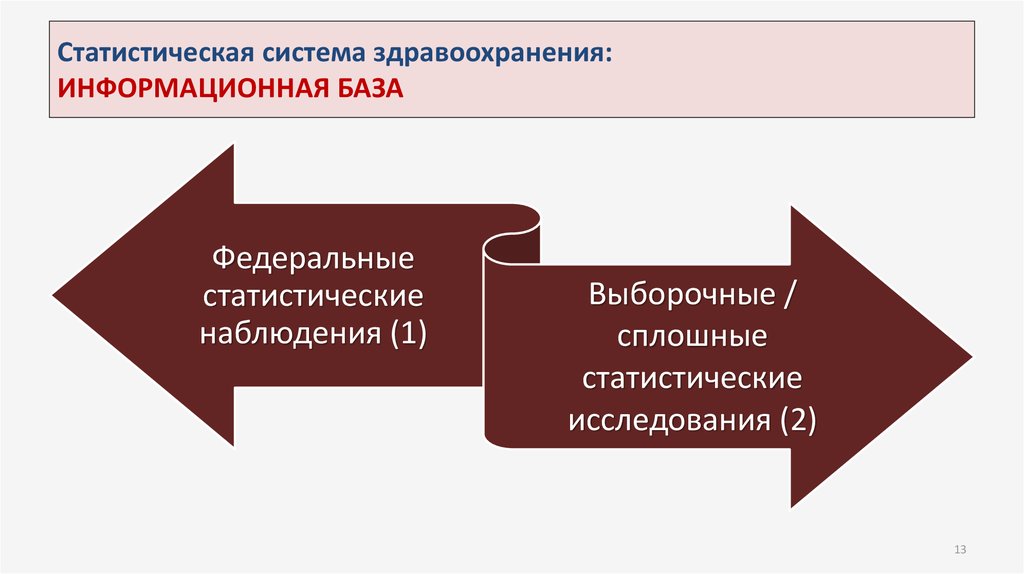
1213. Статистическая система здравоохранения: ИНФОРМАЦИОННАЯ БАЗА
Федеральныестатистические
наблюдения (1)
Выборочные /
сплошные
статистические
исследования (2)
13
14. Статистическая система здравоохранения. ИНФОРМАЦИОННАЯ БАЗА (1). ФЕДЕРАЛЬНЫЕ СТАТИСТИЧЕСКИЕ НАБЛЮДЕНИЯ
Статистическое наблюдение – это массовое, планомерное, научноорганизованное наблюдение за явлениями социальной иэкономической жизни, которое заключается в регистрации
отобранных признаков у каждой единицы совокупности
14
15. Статистическая система здравоохранения. ИНФОРМАЦИОННАЯ БАЗА (1). ФЕДЕРАЛЬНЫЕ СТАТИСТИЧЕСКИЕ НАБЛЮДЕНИЯ
В отечественной статистике используются три организационные формы(типа) статистического наблюдения:
- ОТЧЕТНОСТЬ (предприятий, организаций, учреждений и т. п.)
- СПЕЦИАЛЬНО ОРГАНИЗОВАННОЕ СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ (переписи,
единовременные учеты, обследования сплошного и несплошного характера)
- РЕГИСТРЫ
15
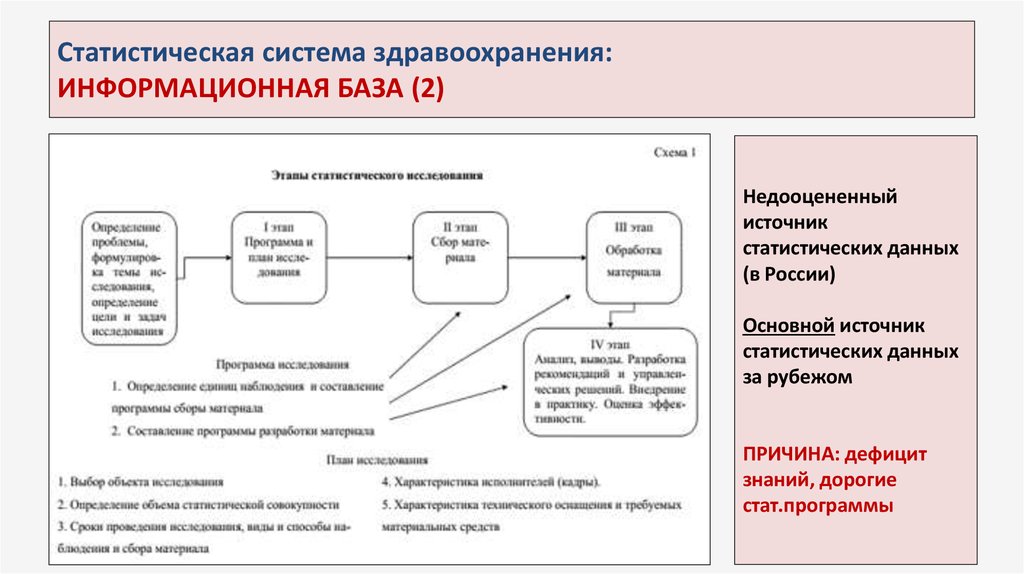
16. Статистическая система здравоохранения: ИНФОРМАЦИОННАЯ БАЗА (2)
Недооцененныйисточник
статистических данных
(в России)
Основной источник
статистических данных
за рубежом
ПРИЧИНА: дефицит
знаний, дорогие
стат.программы
16
17. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ
СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ — это научно организованный по единойпрограмме сбор, сводка и анализ данных (фактов) о социально-экономических,
демографических и других явлениях и процессах общественной жизни в
государстве с регистрацией их наиболее существенных признаков в учетной
документации
17
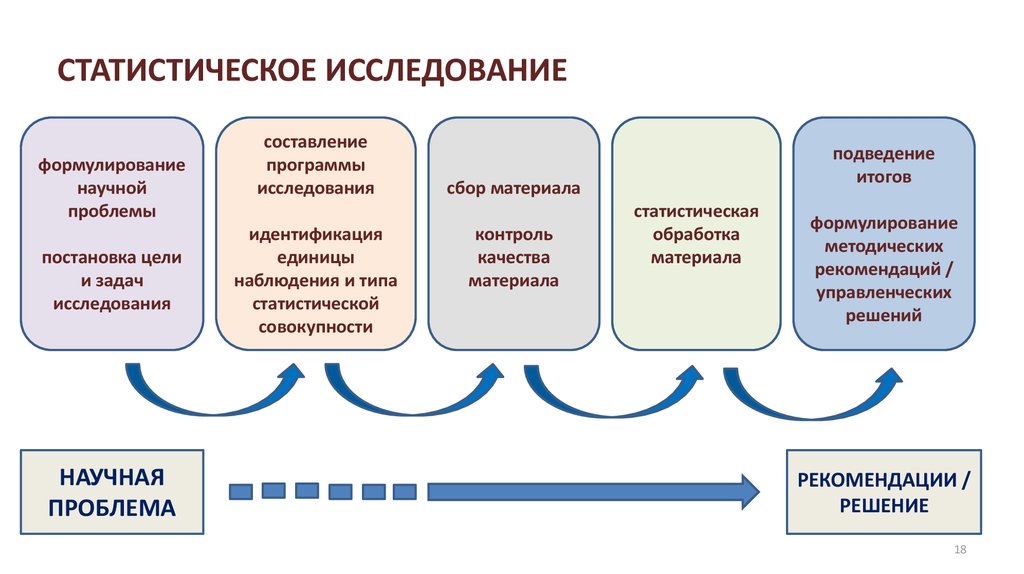
18. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ
формулированиенаучной
проблемы
постановка цели
и задач
исследования
НАУЧНАЯ
ПРОБЛЕМА
составление
программы
исследования
идентификация
единицы
наблюдения и типа
статистической
совокупности
подведение
итогов
сбор материала
контроль
качества
материала
статистическая
обработка
материала
формулирование
методических
рекомендаций /
управленческих
решений
РЕКОМЕНДАЦИИ /
РЕШЕНИЕ
18
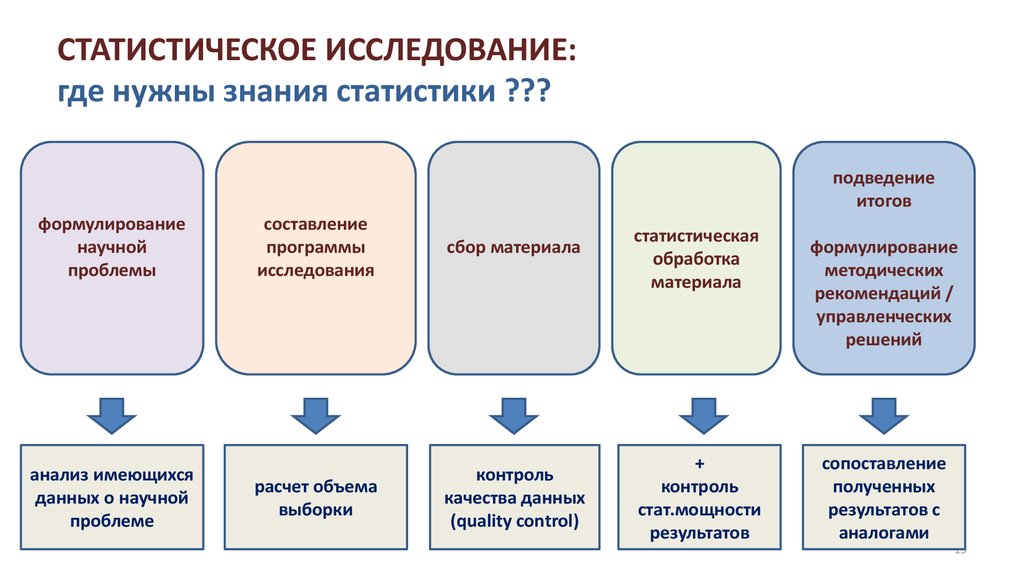
19. СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ: где нужны знания статистики ???
подведениеитогов
формулирование
научной
проблемы
анализ имеющихся
данных о научной
проблеме
составление
программы
исследования
сбор материала
расчет объема
выборки
контроль
качества данных
(quality control)
статистическая
обработка
материала
+
контроль
стат.мощности
результатов
формулирование
методических
рекомендаций /
управленческих
решений
сопоставление
полученных
результатов с
аналогами
19
20. ТИПЫ переменных В СТАТИСТИКЕ
ТИПЫ ПЕРЕМЕННЫХ В СТАТИСТИКЕ20
21.
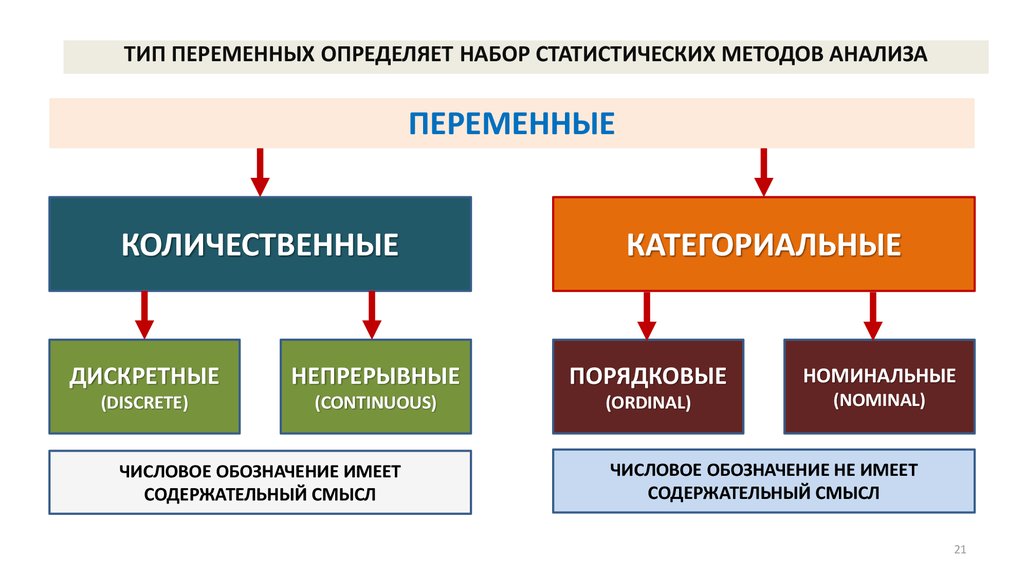
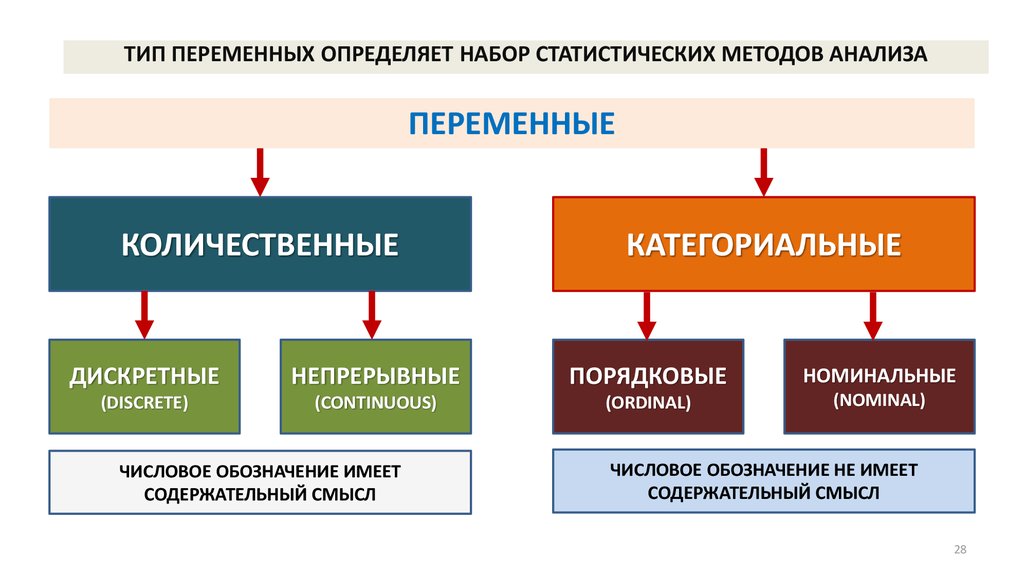
ТИП ПЕРЕМЕННЫХ ОПРЕДЕЛЯЕТ НАБОР СТАТИСТИЧЕСКИХ МЕТОДОВ АНАЛИЗАПЕРЕМЕННЫЕ
КОЛИЧЕСТВЕННЫЕ
КАТЕГОРИАЛЬНЫЕ
ДИСКРЕТНЫЕ
НЕПРЕРЫВНЫЕ
ПОРЯДКОВЫЕ
НОМИНАЛЬНЫЕ
(DISCRETE)
(CONTINUOUS)
(ORDINAL)
(NOMINAL)
ЧИСЛОВОЕ ОБОЗНАЧЕНИЕ ИМЕЕТ
СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ
ЧИСЛОВОЕ ОБОЗНАЧЕНИЕ НЕ ИМЕЕТ
СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ
21
22. КОЛИЧЕСТВЕННЫЕ НЕПРЕРЫВНЫЕ ПЕРЕМЕННЫЕ
МОГУТ ПРИНИМАТЬ ЛЮБЫЕ ЗНАЧЕНИЯ [В НЕКОТОРОМ ЗАДАННОМ ИНТЕРВАЛЕ]0,6 3,5 10,0 19,3 30,2 50,8 78,2
НАИБОЛЕЕ «ПЕРСПЕКТИВНЫЕ» :
- м.б. трансформированы в любые другие переменные
- максимальное количество статистических методов
ПРИМЕРЫ:
- Возраст
- Масса
- Рост
- АД
- Биохимические
показатели
22
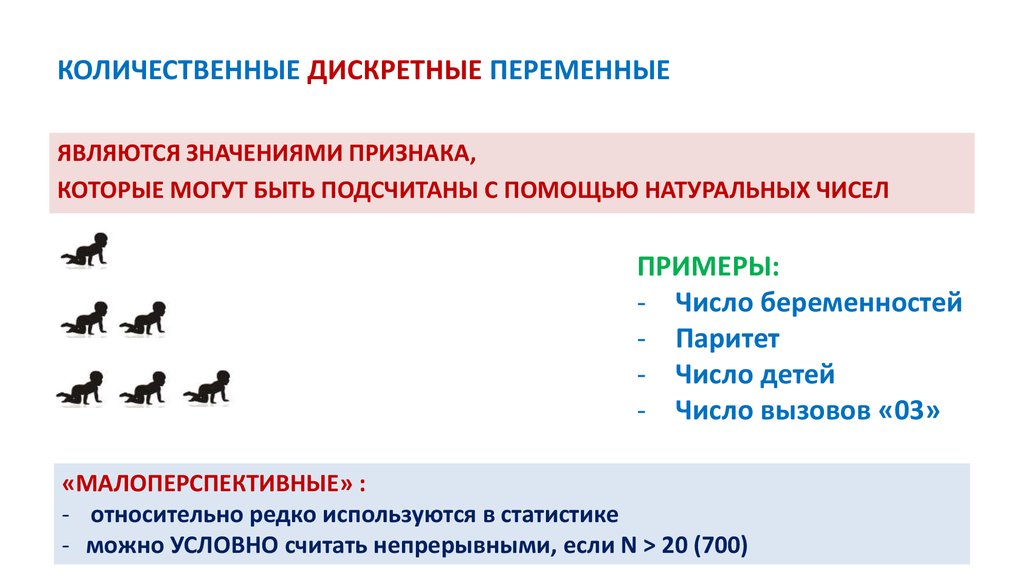
23. КОЛИЧЕСТВЕННЫЕ ДИСКРЕТНЫЕ ПЕРЕМЕННЫЕ
ЯВЛЯЮТСЯ ЗНАЧЕНИЯМИ ПРИЗНАКА,КОТОРЫЕ МОГУТ БЫТЬ ПОДСЧИТАНЫ С ПОМОЩЬЮ НАТУРАЛЬНЫХ ЧИСЕЛ
ПРИМЕРЫ:
- Число беременностей
- Паритет
- Число детей
- Число вызовов «03»
«МАЛОПЕРСПЕКТИВНЫЕ» :
- относительно редко используются в статистике
- можно УСЛОВНО считать непрерывными, если N > 20 (700)
23
24. КАТЕГОРИАЛЬНЫЕ НОМИНАЛЬНЫЕ ПЕРЕМЕННЫЕ
ДАННЫЕ, ДЛЯ КОТОРЫХ НЕТСОДЕРЖАТЕЛЬНОГО ИНТЕРПРЕТИРУЕМОГО ПОРЯДКА
«0»
«1»
ПРИМЕРЫ:
- Пол
- Профессия
- Расовая принадлежность
«ПЕРСПЕКТИВНЫЕ» :
- все чаще используются в статистике – идет развитие соответствующих
методов, в т.ч. регрессионного анализа
24
25. КАТЕГОРИАЛЬНЫЕ ПОРЯДКОВЫЕ ПЕРЕМЕННЫЕ
УРОВЕНЬ ОБРАЗОВАНИЯДАННЫЕ, ДЛЯ КОТОРЫХ ЕСТЬ
СОДЕРЖАТЕЛЬНЫЙ ИНТЕРПРЕТИРУЕМЫЙ ПОРЯДОК
«школа»
«1»
«ГПТУ»
«2»
«университет»
«3»
«аспирантура»
ПРИМЕРЫ:
- Уровень образования
«4» - не в 4 раза лучше, чем «1»
«4»
«ПЕРСПЕКТИВНЫЕ» :
- все чаще используются в статистике – идет развитие соответствующих
методов, в т.ч. регрессионного анализа
25
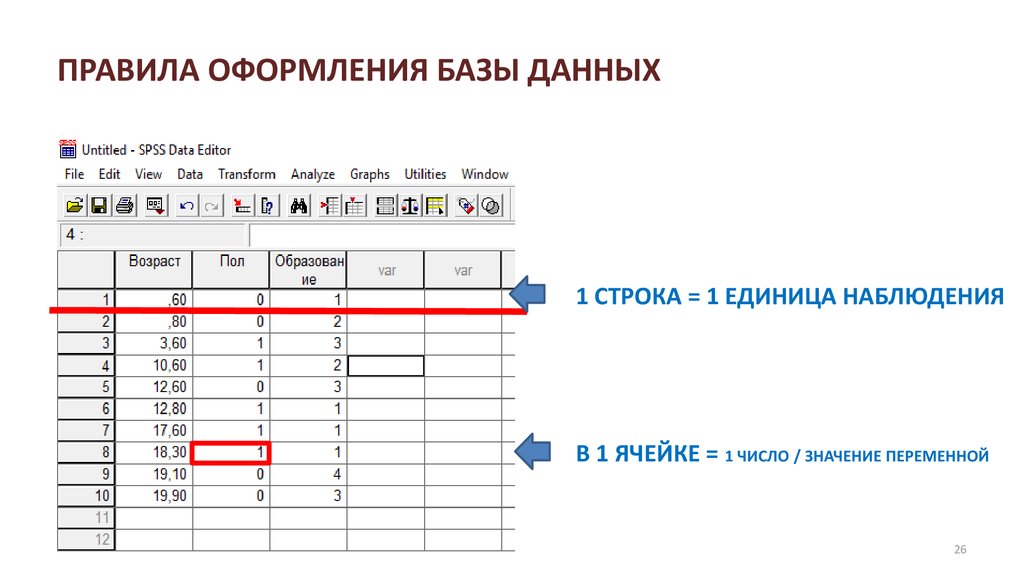
26. ПРАВИЛА ОФОРМЛЕНИЯ БАЗЫ ДАННЫХ
1 СТРОКА = 1 ЕДИНИЦА НАБЛЮДЕНИЯВ 1 ЯЧЕЙКЕ = 1 ЧИСЛО / ЗНАЧЕНИЕ ПЕРЕМЕННОЙ
26
27. СПОСОБЫ ПРЕЗЕНТАЦИИ ДАННЫХ В СТАТИСТИКЕ (ДИСКРИПТИВНАЯ / ОПИСАТЕЛЬНАЯ СТАТИСТИКА)
2728.
ТИП ПЕРЕМЕННЫХ ОПРЕДЕЛЯЕТ НАБОР СТАТИСТИЧЕСКИХ МЕТОДОВ АНАЛИЗАПЕРЕМЕННЫЕ
КОЛИЧЕСТВЕННЫЕ
КАТЕГОРИАЛЬНЫЕ
ДИСКРЕТНЫЕ
НЕПРЕРЫВНЫЕ
ПОРЯДКОВЫЕ
НОМИНАЛЬНЫЕ
(DISCRETE)
(CONTINUOUS)
(ORDINAL)
(NOMINAL)
ЧИСЛОВОЕ ОБОЗНАЧЕНИЕ ИМЕЕТ
СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ
ЧИСЛОВОЕ ОБОЗНАЧЕНИЕ НЕ ИМЕЕТ
СОДЕРЖАТЕЛЬНЫЙ СМЫСЛ
28
29. СПОСОБЫ ПРЕЗЕНТАЦИИ ДАННЫХ В СТАТИСТИКЕ (ДИСКРИПТИВНАЯ / ОПИСАТЕЛЬНАЯ СТАТИСТИКА)
ТИП ПЕРЕМЕННОЙНЕПРЕРЫВНЫЕ
(CONTINUOUS)
ДИСКРЕТНЫЕ
(DISCRETE)
ПОРЯДКОВЫЕ
(ORDINAL)
НОМИНАЛЬНЫЕ
(NOMINAL)
ЧАСТОТНОЕ
РАСПРЕДЕЛЕНИЕ
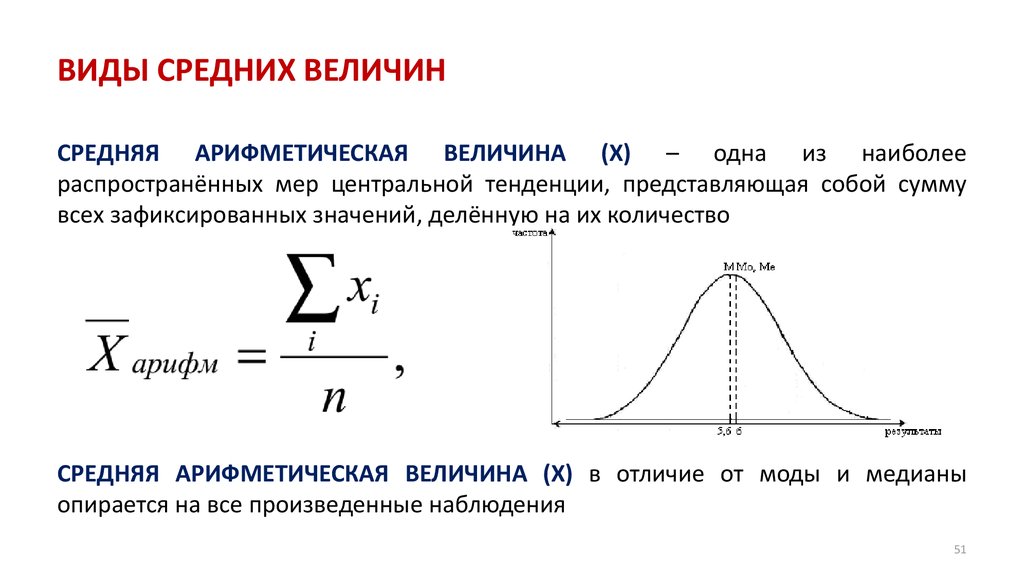
СРЕДНИЕ
ВЕЛИЧИНЫ
ТАБЛИЦЫ /
ГРАФИКИ
+
+
+
+
+
-
+
+
+
+
29
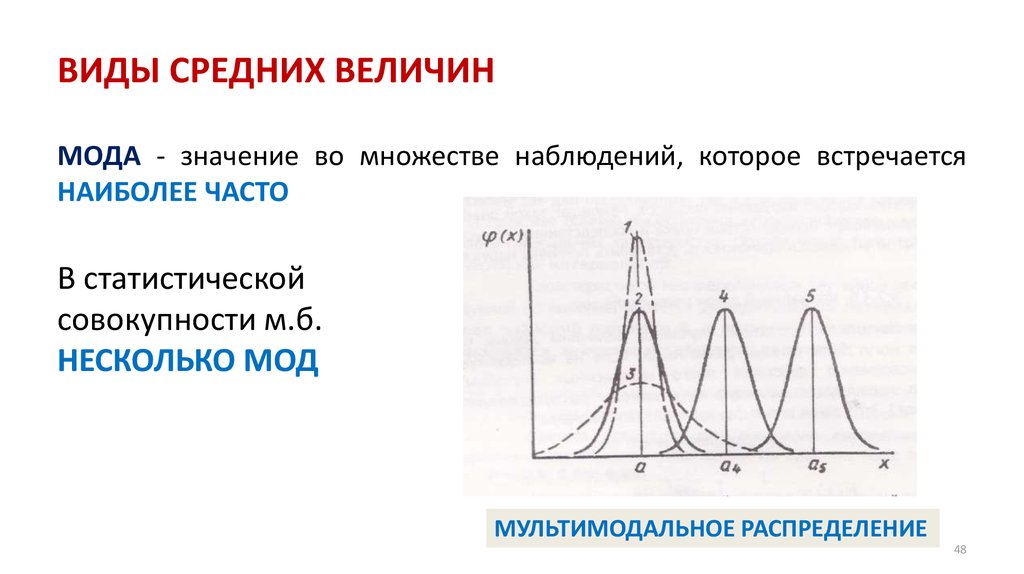
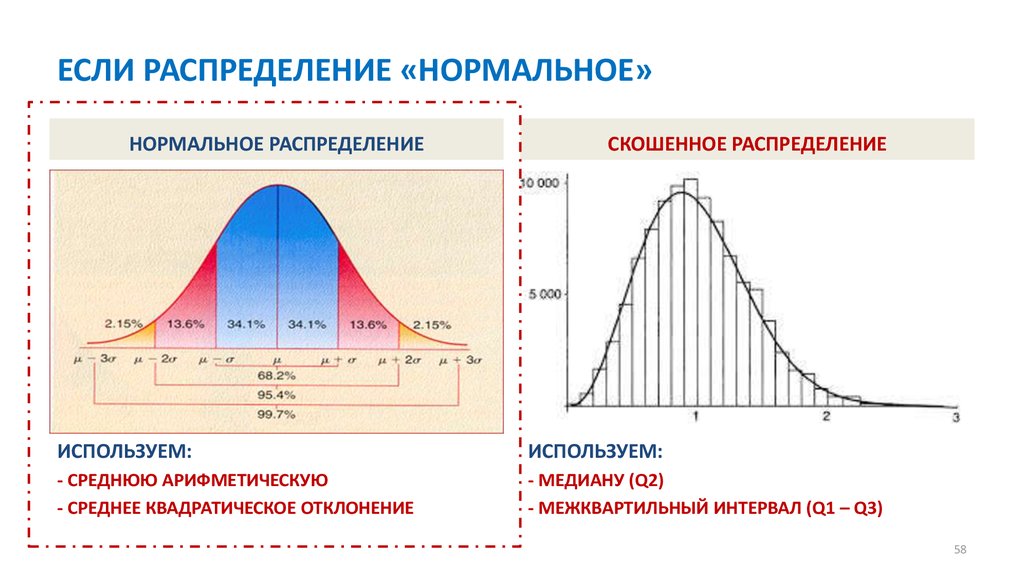
30. ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ
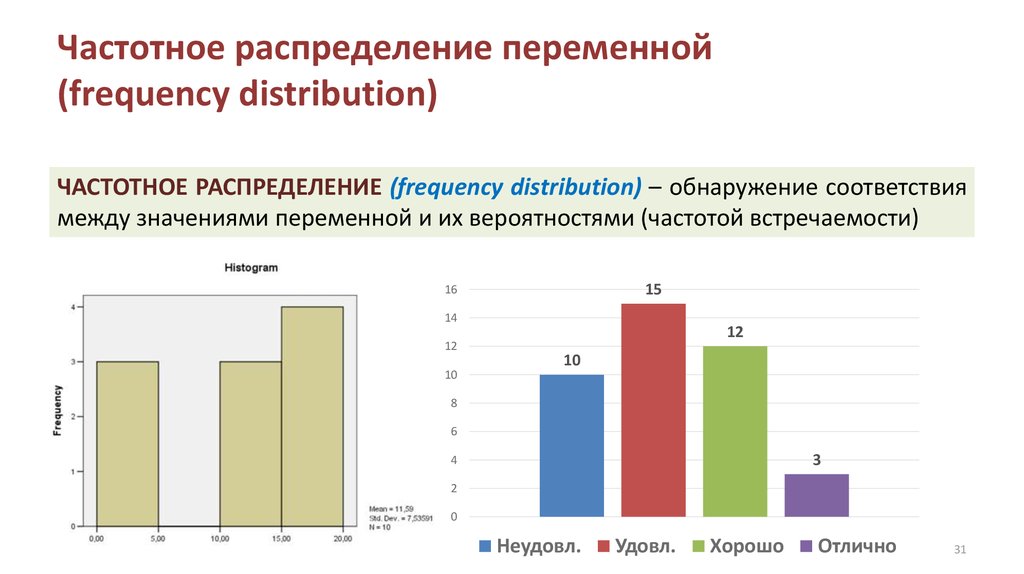
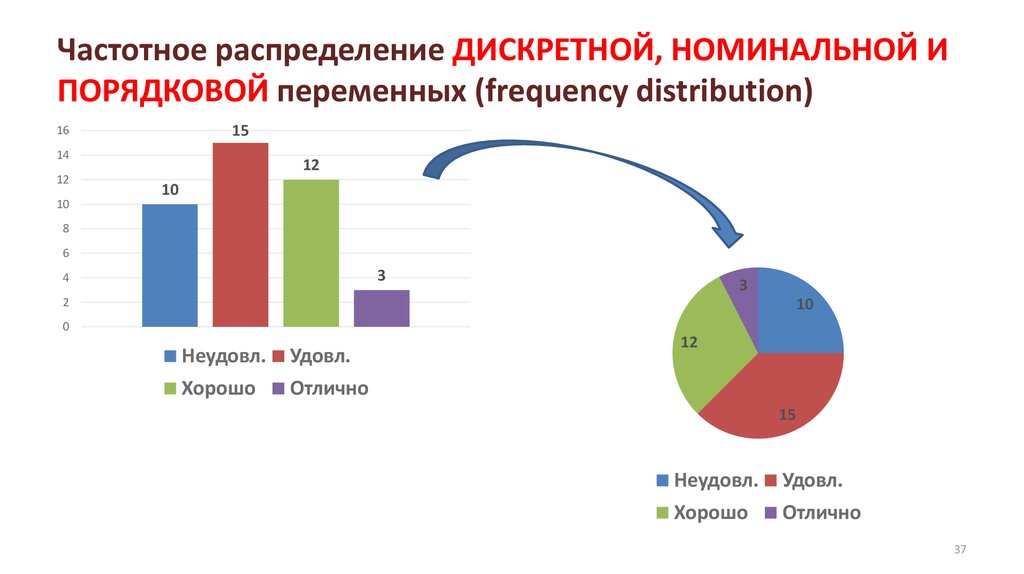
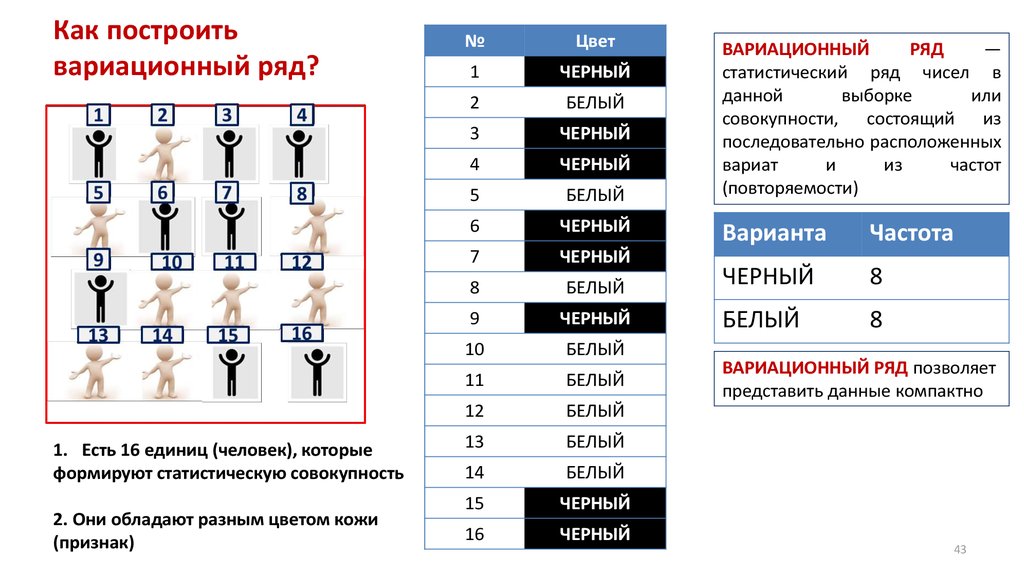
3031. Частотное распределение переменной (frequency distribution)
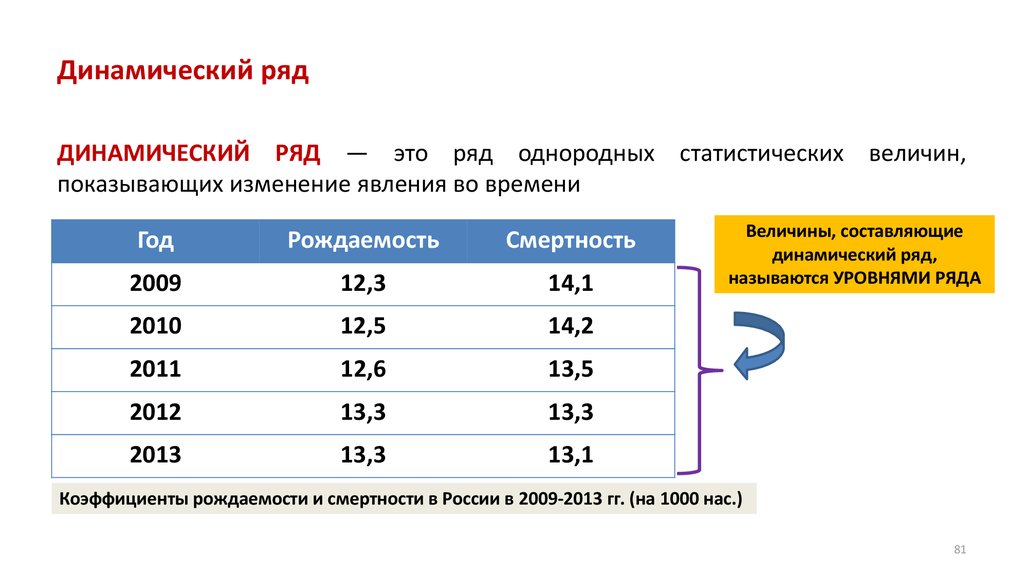
ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ (frequency distribution) – обнаружение соответствиямежду значениями переменной и их вероятностями (частотой встречаемости)
15
16
14
12
10
12
10
8
6
3
4
2
0
Неудовл.
Удовл.
Хорошо
Отлично
31
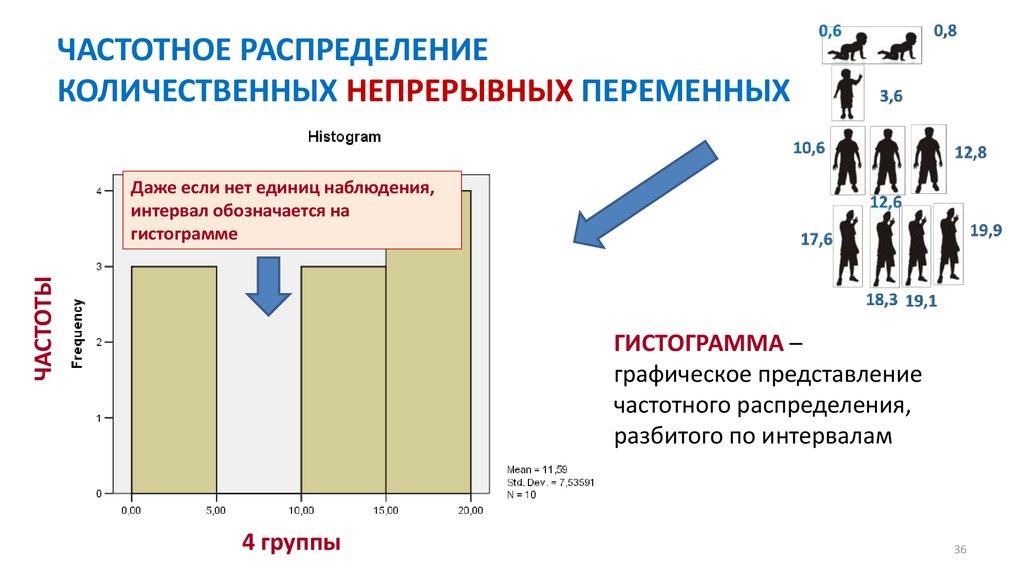
32. ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ НЕПРЕРЫВНЫХ ПЕРЕМЕННЫХ
МОГУТ ПРИНИМАТЬ ЛЮБЫЕ ЗНАЧЕНИЯ [В НЕКОТОРОМ ЗАДАННОМ ИНТЕРВАЛЕ]0,6 3,5 10,0 19,3 30,2 50,8 78,2
ПРИМЕРЫ:
- Возраст
- Масса
- Рост
- АД
- Биохимические
показатели
32
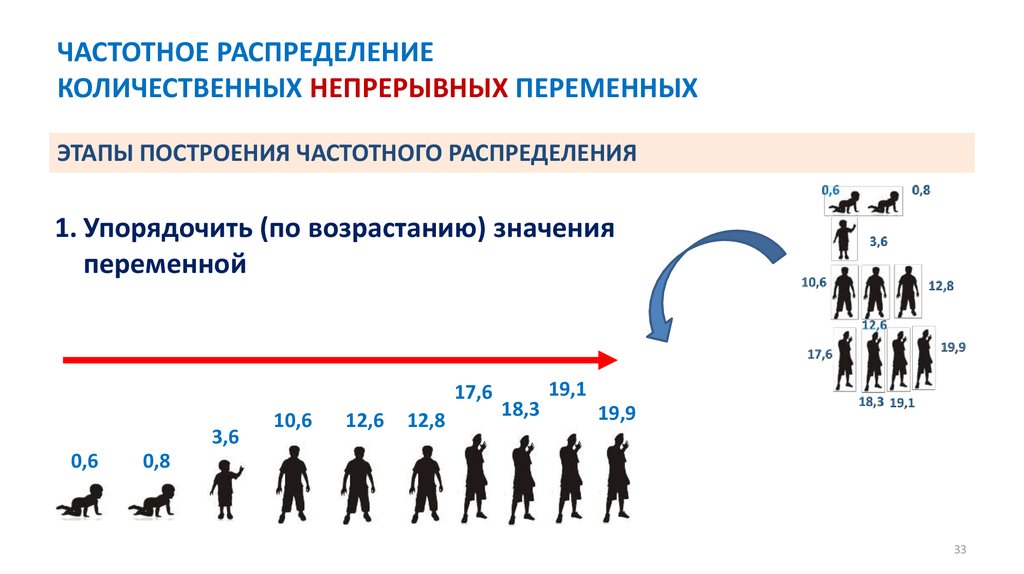
33. ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ НЕПРЕРЫВНЫХ ПЕРЕМЕННЫХ
ЭТАПЫ ПОСТРОЕНИЯ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ1. Упорядочить (по возрастанию) значения
переменной
17,6
3,6
0,6
10,6
12,6
12,8
18,3
19,1
19,9
0,8
33
34. ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ НЕПРЕРЫВНЫХ ПЕРЕМЕННЫХ
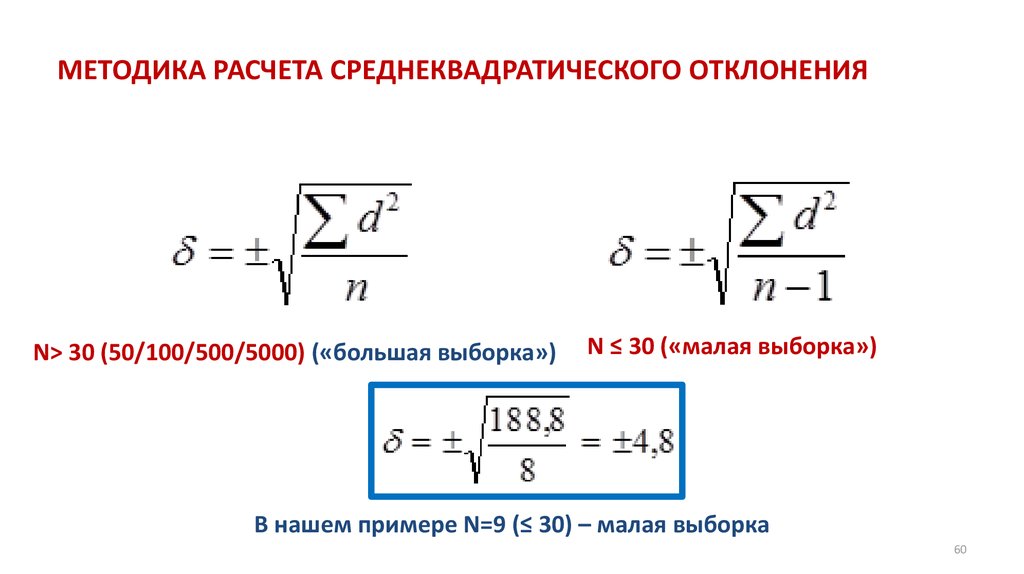
ЭТАПЫ ПОСТРОЕНИЯ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ2. Разбить выборку на группы по равным интервалам (по формуле Стерджесса)
n = 1 + 3.322lgN
n – число групп
N – количество единиц наблюдения
n = 1 + 3.322lg10 = 4
34
35. ЧАСТОТНОЕ РАСПРЕДЕЛЕНИЕ КОЛИЧЕСТВЕННЫХ НЕПРЕРЫВНЫХ ПЕРЕМЕННЫХ
ЭТАПЫ ПОСТРОЕНИЯ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ19,9
3. Рассчитать границы интервалов
0,6
Δ=
Δ=
max −

















































 Математика
Математика








