Похожие презентации:
Метод наименьших квадратов
1. Метод наименьших квадратов.
ВыполнилаСтудентка 2 курса, группа с-15-1б
Иняткина Анна
2.
Метод наименьших квадратовматематический метод, применяемыйдля решения различных задач,
основанный на минимизации суммы
квадратов отклонений некоторых
функций от искомых переменных.
3.
МНК является одним из базовыхметодов регрессионного анализа для
оценки неизвестных параметров
регрессионных моделей по
выборочным данным.
Применяется также для
приближённого представления
заданной функции другими (более
простыми) функциями и оказывается
полезным при обработке наблюдений.
4.
5. Плюсы и минусы данного метода.
+ он приводит к сравнительно простомуматематическому способу определения
параметров а, b, с, … искомого
функционала;
+ он дает довольно веское теоретическое
обоснование с вероятностной точки
зрения.
- основным недостатком МНК является
чувствительность оценок к резким
выбросам, которые встречаются в исходных
данных.
6.
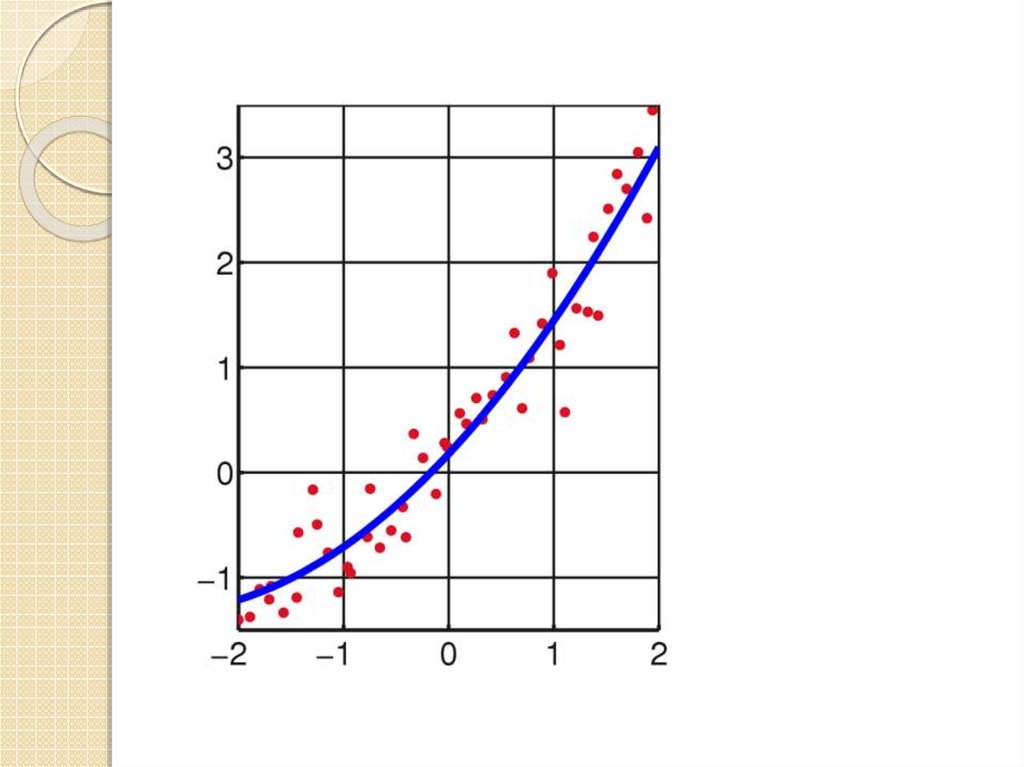
нам нужно подобрать функцию ,график которой проходит как можно
ближе к точкам. Такую функцию
называют аппроксимирующей
(аппроксимация –
приближение) или теоретической
функцией.
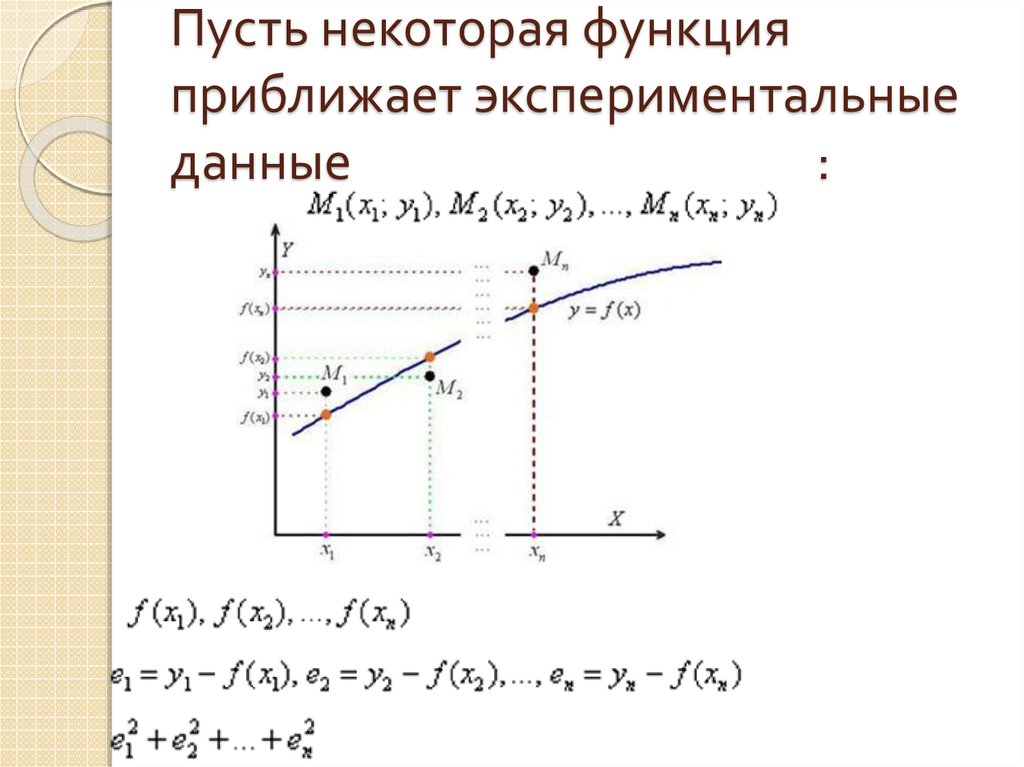
7. Пусть некоторая функция приближает экспериментальные данные :
8.
9.
Иными словами, задача состоит внахождении таких коэффициентов a и b –
чтобы сумма квадратов отклонений
была наименьшей.
10. Вывод формул для нахождения коэффициентов.
11. Из необходимых условий экстремума следует:
12. Алгоритм МНК:
1)2)
3)
4)
5)
Находим суммы
Составляем систему уравнений с
определённым кол-вом неизвестных.
Решаем систему. (метод Крамера)
В результате получаем стационарную
точку S (искомые коэффициенты a;b)
Вычисляем сумму квадратов отклонений
между эмпирическими и теоретическими
значениями.
13. Пример:
Методом наименьших квадратовнайти линейную функцию, которая
наилучшим образом приближает
эмпирические (опытные) данные.
14.
Коэффициенты a, b оптимальнойфункции y=ax+b найдём как решение
системы:
15.
.Таким образом, получаем следующую систему:
16. Проверка:
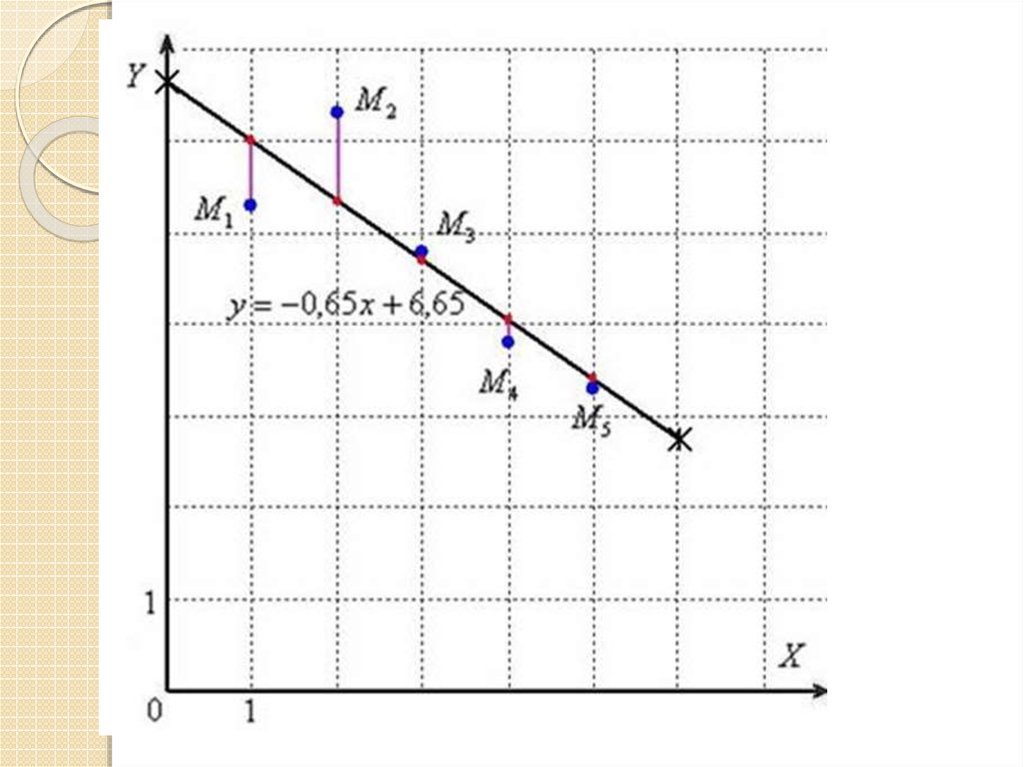
Таким образом, искомая аппроксимирующая функция:Для построения графика аппроксимирующей функции
найдём два её значения:
и выполним чертёж:
















 Математика
Математика








