Регрессионный анализ. Метод наименьших квадратов

1. Лекция №10 «Регрессионный анализ. Метод наименьших квадратов»

МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФАКУЛЬТЕТ ПЕРЕРАБАТЫВАЮЩИХ ТЕХНОЛОГИЙ
 Кафедра технологии хранения и переработки растениеводческой продукции
?????? ?10
«????????????? ??????. ????? ?????????? ?????????»

2. Регрессионный анализ

Регрессионный анализ неразрывно
связан с корреляционным анализом.
Если корреляция позволяет
измерить связь между признаками Х
и У, то регрессионный анализ
позволяет найти форму этой связи с
помощью нахождения уравнения
регрессии.

3. Регрессионный анализ

Если величина Х и У связаны точно
линейной функцией у=в0+в1х1, то
r=±1, а знак будет соответствовать
коэффициенту в1 , если величины Х и
У связаны произвольной
зависимостью, коэффициент имеет
значение -1< r <1.

4. Регрессионный анализ

Найти уравнение регрессии – это значит по
эмпирическим (фактическим) данным
математически описать изменения
взаимно коррелируемых величин.
Рассчитанные по уравнению регрессии
значения результативного признака
называют теоретическим и обычно
обозначают ух (у выровненный по х ) и
рассматривается как функция : у=ƒ(х).

5. Оценка значимости

Выбор теоретической линии регрессии
обусловлен формой эмпирической линии
регрессии, а также с учетом природы
изучаемых показателей и специфики их
взаимосвязи.

6.

Могут использоваться уравнения:
1 у=а0+а1х (прямая)
2 у= а0+а1х+а2х2 (парабола 2-го порядка)
3 у= а0+а11/х (гипербола)
4 у= а0а1х (показательная функция)
5 у= а0+blgx (логарифмическая)

7.

Обычно зависимость, выражаемую
уравнением прямой, называют
прямолинейной, а все остальное –
криволинейными.
Выбрав тип функции, по
эмпирическим данным определяют
параметры уравнения.

8. Регрессионная прямая

Существует несколько методов нахождения
параметров уравнения регрессии. Наиболее
часто используется метод наименьших
квадратов (МНК).
Суть метода заключается в следующем искомые
теоретические значения результативного
признака ух должны быть такими, при
которых бы обеспечивалась минимальная
сумма квадратов их отклонений от
эмпирических значений, т.е.
n
S ( yi y x ) min
i 1

9.

Предполагается что разброс точек относительно кривой подчиняется закону
нормального распределения.
Зависимость переменной у от х может выражаться формулой:
y f (x)
У – зависимая, х – независимая переменная.
y b0 b1 x

10.

Если же х представляет зависимую,
а у независимую, то речь идет о
регрессии х по у
х b0 b2 у
Величины b0, b1, b2 – коэффициенты
регрессии, постоянные величины.

11.

Они вычисляются по формулам:
b1
( x x)( y y )
( x x)
i
i
2
i
b0 y b1 x
Где хi и уi – частные эмпирические
значения изучаемых величин.

12.

Оценка значимости коэффициентов
уравнения регрессии проводится по
критерию Стьюдента:
(bi )
tp
Sbi
Где bi – коэффициенты уравнения регрессии;
Sbi – среднее квадратичное отклонение для
коэффициентов уравнения регрессии b0 и
b1 находят:

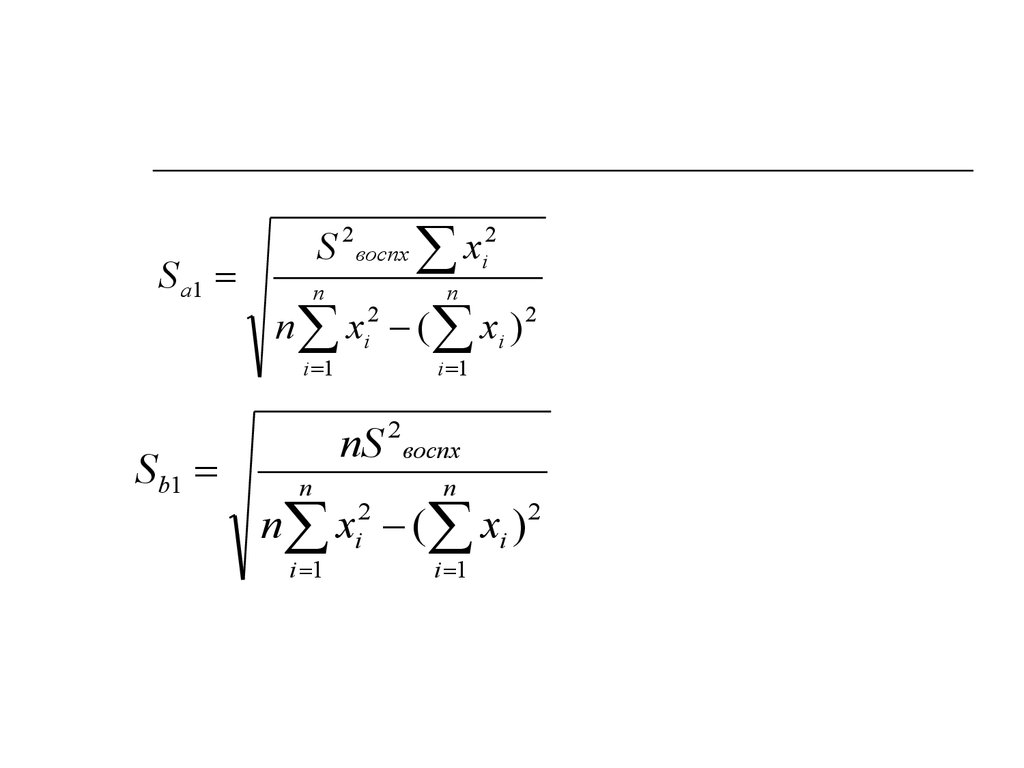
13.

S a1
Sb1
S 2 воспx xi2
n
n
i 1
i 1
n xi2 ( xi ) 2
nS
2
воспx
n
n
i 1
i 1
n xi2 ( xi ) 2

14.

Дисперсию воспроизводимости
определяют:
n
2
S восп
2
(
y
y
)
i
i 1
n 1
где n – количество экспериментов.
Если tрасч> tтабл, то коэффициент
значим.

15.

Адекватность уравнения проверяют по критерию
Фишера:
Fрасч
2
S ад
2
S воспр
Дисперсия адекватности определяется
уравнением:
n
2
S ад
2
ˆ
(
y
у
)
i i
i 1
Где l – число
n l значимых коэффициентов в
уравнении регрессии
(n-l) – число степеней свободы адекватности.

16.

При постановке ряда экспериментальных задач
необходимо не только нахождение уравнения
регрессии, описывающего зависимость тех или
иных факторов, но и поиск их оптимальных
значений.
Существует ряд методов оптимизации – метод
золотого сечения, метод координатного спуска,
метод спирального координатного спуска.
Задачи оптимизации, независимо от метода ставят
таким образом: поиск уравнения регрессии и
дальнейший анализ его с поиском наилучших
результатов.