Композиция. Пропорции. Клетка

1. Композиция. Тема № 7.

Пропорции.
Клетка.

2. Законы гармонии

• Закон единства и соподчинения
• Закон равновесия.
• Ритм
• Контраст
• Нюанс,
• Тождество
• Пропорции
• Масштаб

3. Во времена Гомера (древняя Греция)

• Гармониями называли скрепы,
соединяющие доски в обшивке корабля.
Лишенный гармоний корабль
распадался на отдельные доски.
• Важнейшее средство гармонизации –
Пропорции ( связи частей и
целого)

4.

5. Пропорции и есть то средство в котором заложена идея соотношения целого и составляющих это целое частей.

6.

7. В искусстве- пропорции- размерные соотношения элементов формы

В искусствепропорцииразмерные
соотношения
элементов формы

8. Начиная с древнегреческих философов, математиков, художников проводились теоретические исследования для нахождения самых

совершенных
гармоничных пропорций

9.

10. Гармония- соразмерность частей, слияние различных компонентов объекта в единое органичное целое. В греческой Философии гармония

рассматривалась как
организованность космоса,
в Эстетике- как характеристика
прекрасного.

11.

12.

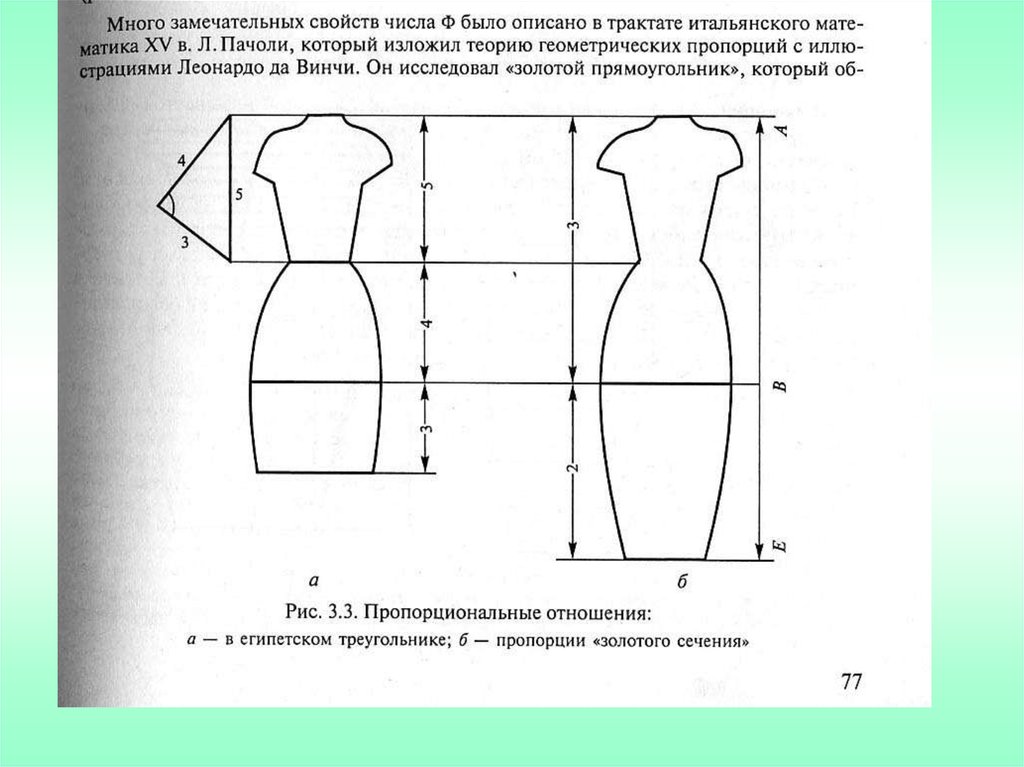
13. Пропорции можно разделить на две группы: 1. простые «египетский треугольник» с гармоничными соотношениями сторон – 3:4:5

14.

15. Архитектор эпохи Возрождения Альберти писал: «Существуют числа, благодаря которым гармония звуков пленяет слух, эти же числа

преисполняют и
глаза , дух чудесным
наслаждением.»

16. Древние греки вывели иррациональное число Ф(фи),которое символизировало пропорции «ЗОЛОТОГО СЕЧЕНИЯ» Буква Ф первая буква в

имени
великого скульптора Фидия,
который часто использовал
пропорции « золотого сечения»
в своих скульптурах.

17. Число Фи

1,62 = /3:2/
• 0,6666666……= 2:3
• Число иррациональное

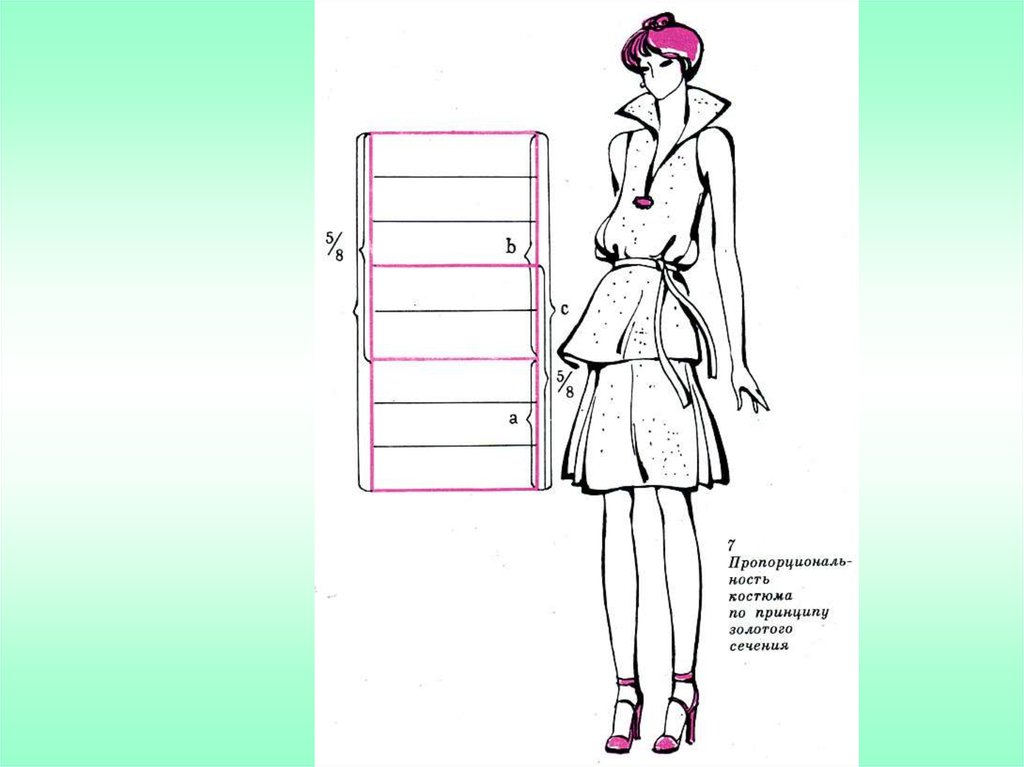
18. Золотое сечение

• В некотором приближении
отношения
• « золотого сечения»
• можно представить в виде
ряда: 2/3; 3/5; 5/8; 8/13…..

19.

20. Термин «Золотое сечение» сформулировал немецкий ученый А. Цейзинг в 19 веке и дал ему определение: 1. «Золотое

сечение»господствует в
архитектуре
2. «Золотое сечение»господствует в в
природе.
3. «Золотое сечение»господствует в
архитектуре именно потому, что оно
господствует в природе

21. Числа Фибоначчи

• 1,2,3,5,8,13,21,34……..
• Каждое последующее число,
начиная с третьего, равно
сумме двух предыдущих, их
придумал математик
Леонардо из Пизы по
прозвищу Фибоначчи

22. Иллюзию постепенного едва заметного убывания дают динамические квадраты Фибоначчи

23. Таким образом, гармоничные пропорциональные соотношения основаны на неравенстве пропорций.

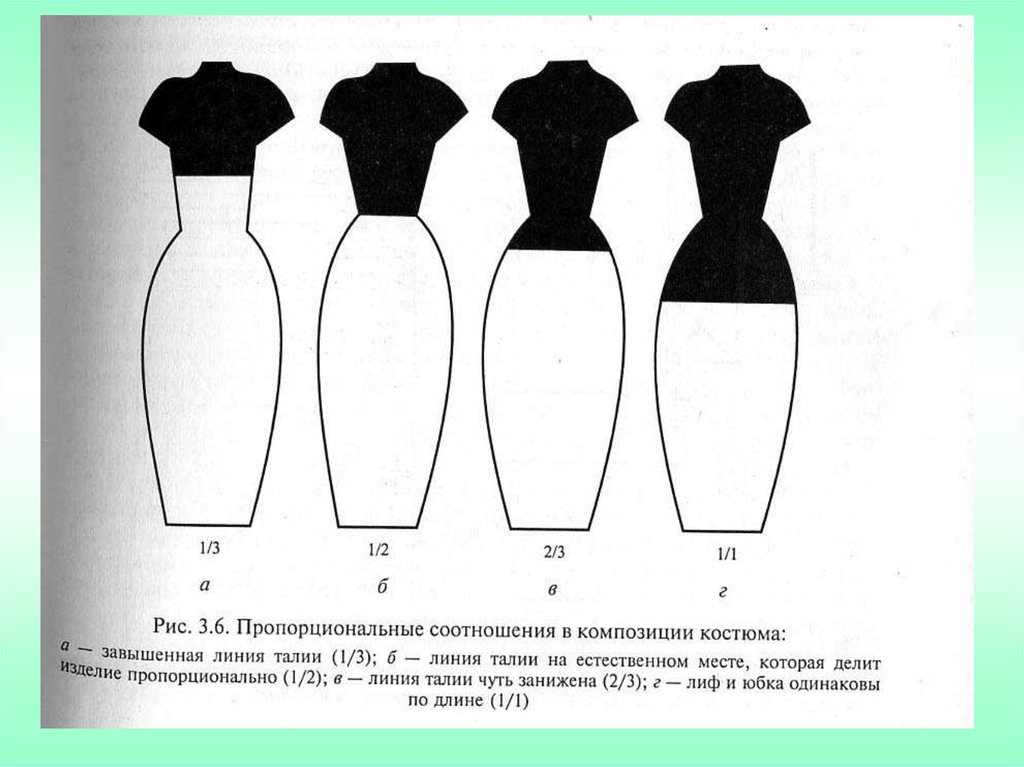
24. В моделировании одежды простые пропорциональные соотношения выражаются дробным числом, от1 до 8. Например: рукав ¾; мини

юбка1/3; пальто
7/8;, свитер 2/3 от целого.

25.

26.

27. Пропорции определяются интуитивно или задаются тенденциями моды. Каждое модное направление предлагает свои пропорциональные

членения костюма
и человека в костюме.

28.

29. Пропорции мужчин разного возраста

30.

31.

32.

33.

34.

35.

36.

37. задание

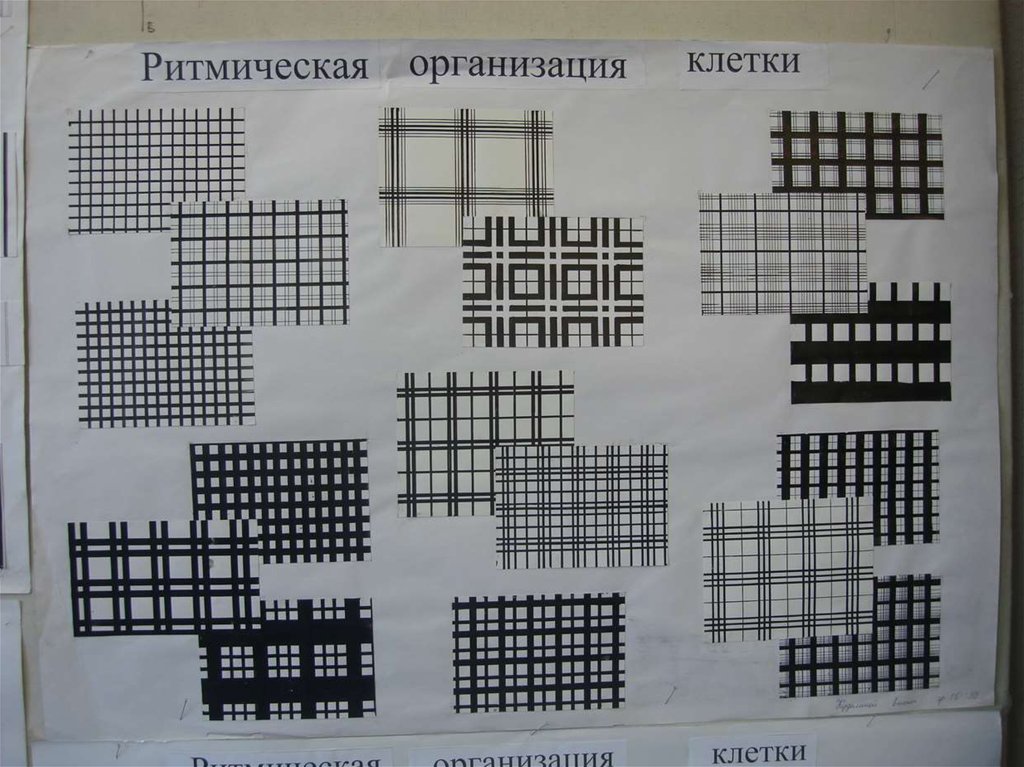
• 1. создать 7 эскизов клетки. Разных по
решению.
• А. Использовать линии разной толщины.
• Б. Использовать 2-3 серые тональные полосы
в некоторых клетках.
• В. Использовать гармоничные пропорции
полос и промежутков.
• Г. Использовать фактуру в широких полосах
некоторых эскизов.

38. Задание 2.

• Создать 5 эскизов костюмов разных
пропорциональных решений внешних и
внутренних разработок.
• из них 3 эскиза должны иметь
орнаментальное использование клетки,
разработанной ранее.