Вектора. Кинематика. Лекция №1

1.

Курс общей физики
Механика
Лекция №1
Вектора
Кинематика
к.ф.-м.н., доцент ШЕН
Стеблий Максим Евгеньевич
г. Владивосток
2019

2.

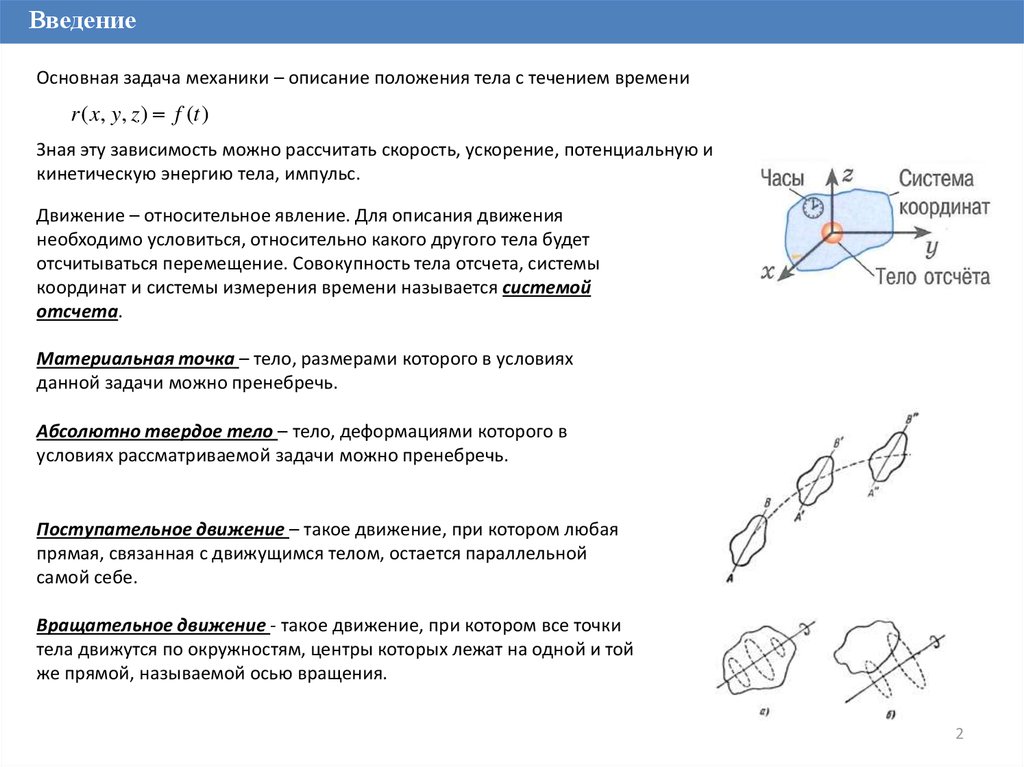
Введение
Основная задача механики – описание положения тела с течением времени
r ( x, y, z ) f (t )
Зная эту зависимость можно рассчитать скорость, ускорение, потенциальную и
кинетическую энергию тела, импульс.
Движение – относительное явление. Для описания движения
необходимо условиться, относительно какого другого тела будет
отсчитываться перемещение. Совокупность тела отсчета, системы
координат и системы измерения времени называется системой
отсчета.
Материальная точка – тело, размерами которого в условиях
данной задачи можно пренебречь.
Абсолютно твердое тело – тело, деформациями которого в
условиях рассматриваемой задачи можно пренебречь.
Поступательное движение – такое движение, при котором любая
прямая, связанная с движущимся телом, остается параллельной
самой себе.
Вращательное движение - такое движение, при котором все точки
тела движутся по окружностям, центры которых лежат на одной и той
же прямой, называемой осью вращения.
2

3.

Вектор
Траектория – кривая, описываемая некоторой точкой при движении. Длина
этой кривой – пройденный путь (S).
Перемещение – отрезок, соединяющий начало и конец траектории (r12).
Характеризуется длиной и направлением – векторная величина.
Величина, для описания которой достаточно одного числового значения –
скалярная величина.
Представление вектора:
1) две точки
A(a x , a y , a z ); B(bx , by , bz )
2) радиус-вектор - вектор, задающий
положения точки в пространстве относительно начала
координат.
r AB (bx ax , by a y , bz az )
3) через базис – упорядоченный набор векторов,
такой, что любой вектор пространства может быть
единственным образом представлен в виде линейной
комбинации векторов из этого набора.
r rx i ry j rz k
i, j, k - единичные вектора или орты — вектор, длина которых равна единице.
3

4.

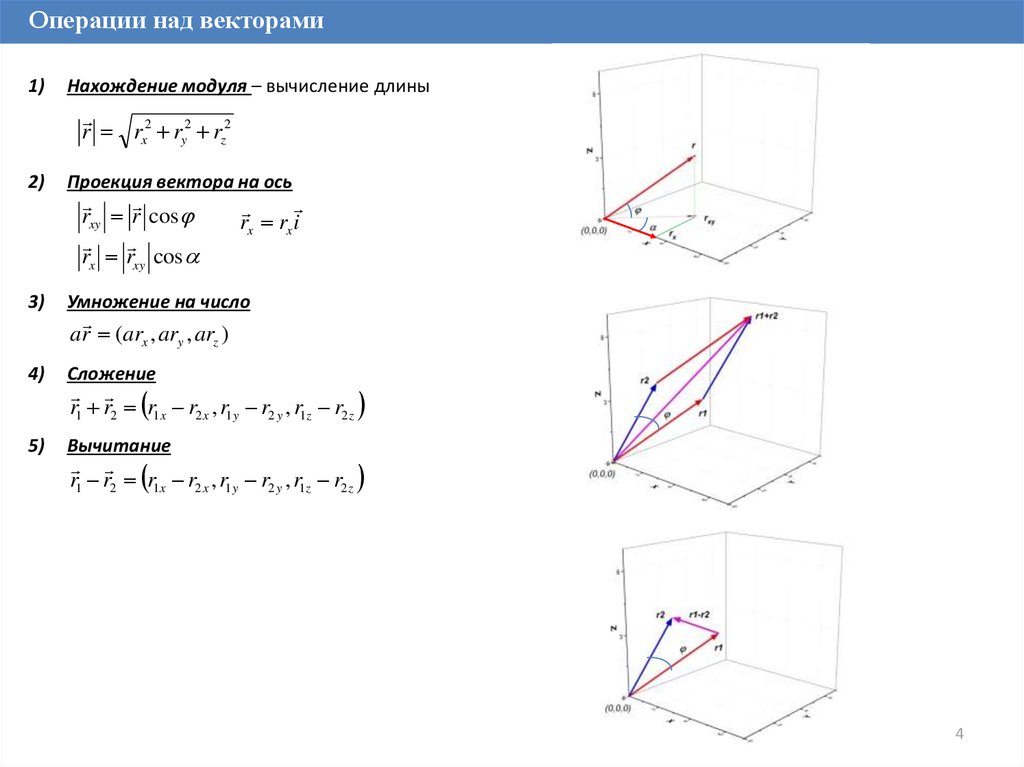
Операции над векторами
1)
Нахождение модуля – вычисление длины
r rx2 ry2 rz2
2)
Проекция вектора на ось
rxy r cos
rx rxy cos
rx rx i
3)
Умножение на число
4)
Сложение
5)
Вычитание
ar (arx , ary , arz )
r1 r2 r1x r2 x , r1 y r2 y , r1z r2 z
r1 r2 r1x r2 x , r1 y r2 y , r1z r2 z
4

5.

Операции над векторами
6)
Скалярное произведение векторов - операция над двумя векторами,
результатом которой является число, характеризующее длины
векторов-сомножителей и угол между ними.
ab a b cos( a , b )
ab a x bx a y by a z bz
7)
- через длины и угол
- через координаты
Векторное произведение векторов вектор, перпендикулярный обоим исходным
векторам, норма которого равна площади параллелограмма,
образованного исходными векторами, а направление которого
определяется по правилам правого винта.
с ab a b
c a b a b sin( a, b )
вращаем винт от первого
множителя ко второму
- обозначение
- длина вектора
a (a x , a y , a z )
b (bx , by , bz )
i
j k
ab a x a y a z
bx
by
bz
ab a y bz a z by , a z bx a x bz , a x by a y bx
- координаты результирующего вектора
5

6.

Скорость. Ускорение.
Положение материальной точки в пространстве зададим радиус-вектором r.
Перемещение точки за время Δt будет соответствовать изменению радиусвектора Δr, не совпадающему в общем случае с ΔS.
r
s dr ds
lim
lim
t 0 t
t 0 t
dt dt
м / c
y
ΔS
a
V1
Скорость – векторная физическая величина, характеризующая
быстроту перемещения и направление движения материальной
точки относительно выбранной системы отсчёта. Предел отношения
dr к dt. Касательная к траектории.
r1 Δr
V2
r2
x
В общем случае, в прямоугольной декартовой системе координат,
скорость определяется
xi y j z k
dx dy dz
i
j k
dt
dt
dt
Пройденный путь
S lim
t 0
t2
N
t (t )dt
i 1
i
i
t1
6

7.

Скорость. Ускорение.
Скорость – векторная физическая величина, характеризующая
быстроту перемещения и направление движения материальной
точки относительно выбранной системы отсчёта. Предел отношения
dr к dt. Касательная к траектории.
r
s dr ds
lim
lim
t 0 t
t 0 t
dt dt
y
м / c
ΔS
a
V1
r1 Δr
V2
r2
Ускорение — векторная физическая величина, определяющая
быстроту изменения скорости тела, то есть первая производная
от скорости по времени.
dv
a lim
t 0 t
dt
a м / c 2
t
0 adt
x
В общем случае, в прямоугольной декартовой системе
координат, ускорение определяется
d 2x d 2 y d 2z
a 2 i 2 j 2 k
dt
dt
dt
0
0 at
Пройденный путь при равнопеременном движении
t
at 2
S ( 0 at )dt 0t
2
0
7

8.

Ускорение при криволинейном движении
Рассмотрим движение по окружности радиусом R с постоянной скоростью υ.
За время Δt точка сместиться из положения 1 в положение 2, совершив
поворот на угол Δϕ и пройдя путь ΔS. Перенесем вектор скорости из точки 2 в
точку 1 и найдем разность этих векторов. Получим равнобедренный
треугольник 134. Вектор Δυ имеет направление n.
Ускорение можно представить в виде:
/ 2
sin
(sin )
2
2
То же самое сделаем для треугольника 012:
S / 2
2
R
2
τ
3
n
υ
2
4
a lim
lim
n
t 0 t
t 0 t
Выразим ускорение через известные величины R и υ. Рассмотрим
треугольник 134. Опустим перпендикуляр и учтем, что для малых углов:
sin
1
R
Рассмотрим случай криволинейного движения. Ускорением называется
изменение скорости, но скорость – векторная величина, а то есть, может
изменятся как по величине, так и по направлению.
S
R
1
0
0
Δυ/2
3
Δυ
ΔS/2
4
1
ΔS
Представим эти выводы в формулу для ускорения:
S
S
a lim
n lim
n lim
n n lim
n
t 0 t
t 0
t 0 R t
t
R t 0 t R
2
an
n
R
При стремлении Δϕ, а значит и ΔS, к нулю,
вектор n’ совпадет по направлению с
нормалью n (перпендикуляром) к скорости υ.
Нормальное ускорение - компонента ускорения точки, характеризующая быстроту изменения направления 8
вектора скорости для траектории с кривизной 1/R, направлено к центру кривизны траектории.
2

9.

Ускорение при криволинейном движении
1
υ
3
τ
n
Если движение криволинейное (не окружность), то вектор скорости υ
изменяется как по направлению, так и по величине. Изменение вектора
скорости Δυ можно разложить на компоненты: Δυτ и Δυn, сонаправленные с
единичными векторами n’ и τ’ (при стремлении Δϕ к нулю, эти вектора
совпадут c векторами n и τ).
2
4
τ’
R
В общем виде ускорение можно найти представив скорость в виде (величина
скорости умножить на направление скорости):
d ( ) d
d
a
dt
dt
dt
Производная произведения. Вторая компонента описывает изменение
скорости по направлению, значение было найдено ранее.
0
d 2
a an a
n
dt
R
2 2
a an a
Тангенциальное ускорение aτ — компонента ускорения, направленная
по касательной к траектории движения. Характеризует изменение модуля скорости.
Нормальное ускорение an - компонента ускорения точки, характеризующая быстроту
изменения направления вектора скорости для траектории с кривизной 1/R, направлено
к центру кривизны траектории.
9

10.

Вращательно движение
При вращательном движение все точки твердого тела движутся по окружностям, центры которых лежат на
общей оси OO. Радиус вектор каждой точки ri за время Δt поворачивается на один и тот же угол Δϕ. При
этом пройденный путь ΔSi может быть разным.
Вращательное движение характеризуется угловой скоростью ω.
Угловая скорость – векторная физическая величина, характеризующая изменение углового
положения материальной точки относительно центра вращения. Указывает направление
вращения и численно равна углу описываемому радиус-вектором точки за единицу времени.
d
t 0 t
dt
lim
рад / c
Вектор угловой скорости ω всегда ориентирован вдоль оси вращения.
Направление вектора ω определяется по правилу правого винта: искомый вектор ориентирован
по направлению поступательного движения правого винта при его повороте, совпадающем с
направлением вращения рассматриваемой точки.
Вращение с постоянной угловой скоростью характеризуется временем полного оборота – период T.
2
2
T c
T
T
Величина обратная периоду называется частотой вращения, соответствует числу оборотов за
единицу времени.
1
T
c 1 Герц
Изменение угловой скорости, как по величине, так и по направлению, характеризуется угловым
ускорением:
d
t 0 t
dt
lim
рад / c
2
Вектор углового ускорения β сонаправлен с вектором угловой скорости ω если точка ускоряется, и
направлен противоположно, если точка замедляется.
10

11.

Связь поступательного и вращательного движения
Во вращающемся теле угловая скорость ω всех точек одинакова. Однако в
зависимости от радиуса описываемой окружности R точки могут проходить разный
путь ΔS, а значит будут иметь разную линейную скорость υ. Найдем взаимосвязь
между угловой и линейной скоростью.
За время Δt точка повернется на угол Δϕ. Точка находящаяся на расстояние R от оси
вращения, проходит при этом путь ΔS. Выразим пройденный путь через угол
рассматривая равнобедренный треугольник 012 (как в случае нахождения
нормального ускорения):
ω
0
S R
Подставим это выражение в формулу определения скорости:
2
1
S
R lim
R
t 0 t
t 0 t
lim
Полученная взаимосвязь интересна тем, что все три величины уравнения являются
векторными: вектор угловой скорости ω направлен по оси, радис-вектор R проводится
от оси вращения до точки, линейная скорость υ – касательная к траектории.
Если результатом перемножения двух векторов является третий вектор,
ориентированный перпендикулярно плоскости образованной двумя исходными
векторами, то такая взаимосвязь описывается векторным произведением:
R
11