Похожие презентации:
Сечения
1. СЕЧЕНИЯ.
Сабля Татьяна Евгеньевнаучитель математики
Лицей № 488
Выборгский район
Санкт-Петербург.
СЕЧЕНИЯ.
2.
1.СЕЧЕНИЕ.
2
3.
Разрежем тетраэдр на какие-нибудь две части.Многоугольник, полученный
на срезе, называют
сечением тетраэдра
4.
Таким образом можно получить сечение любогомногогранника.
Например:
5.
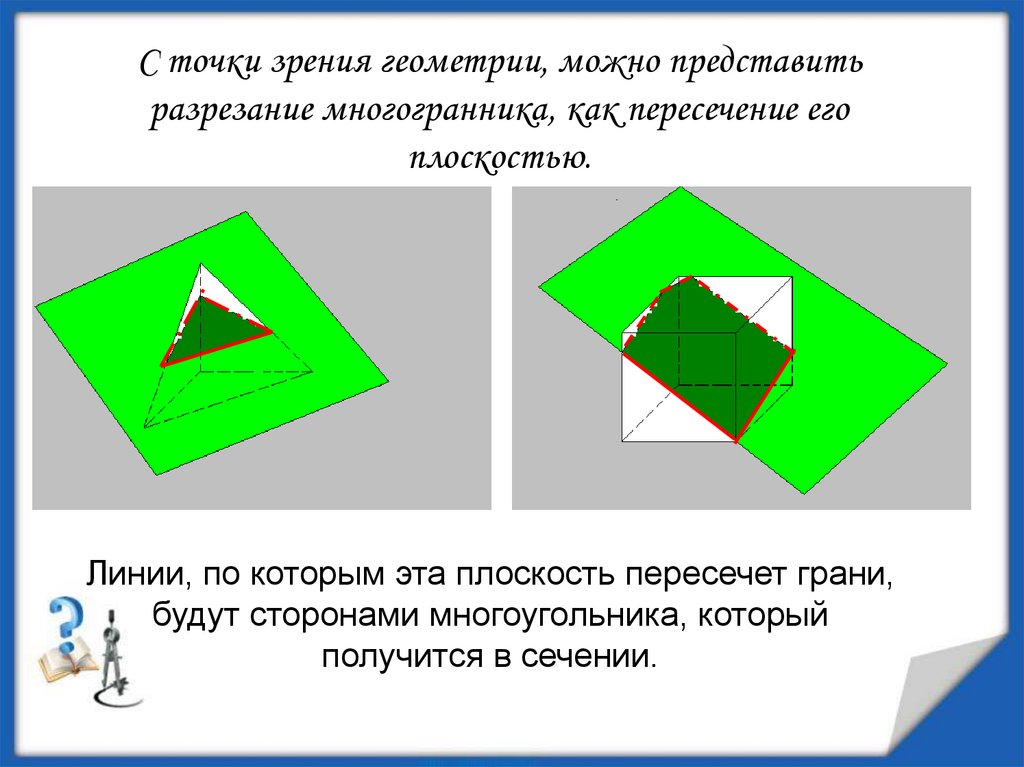
С точки зрения геометрии, можно представитьразрезание многогранника, как пересечение его
плоскостью.
Линии, по которым эта плоскость пересечет грани,
будут сторонами многоугольника, который
получится в сечении.
6.
2.«Особенности»
сечений.
6
7.
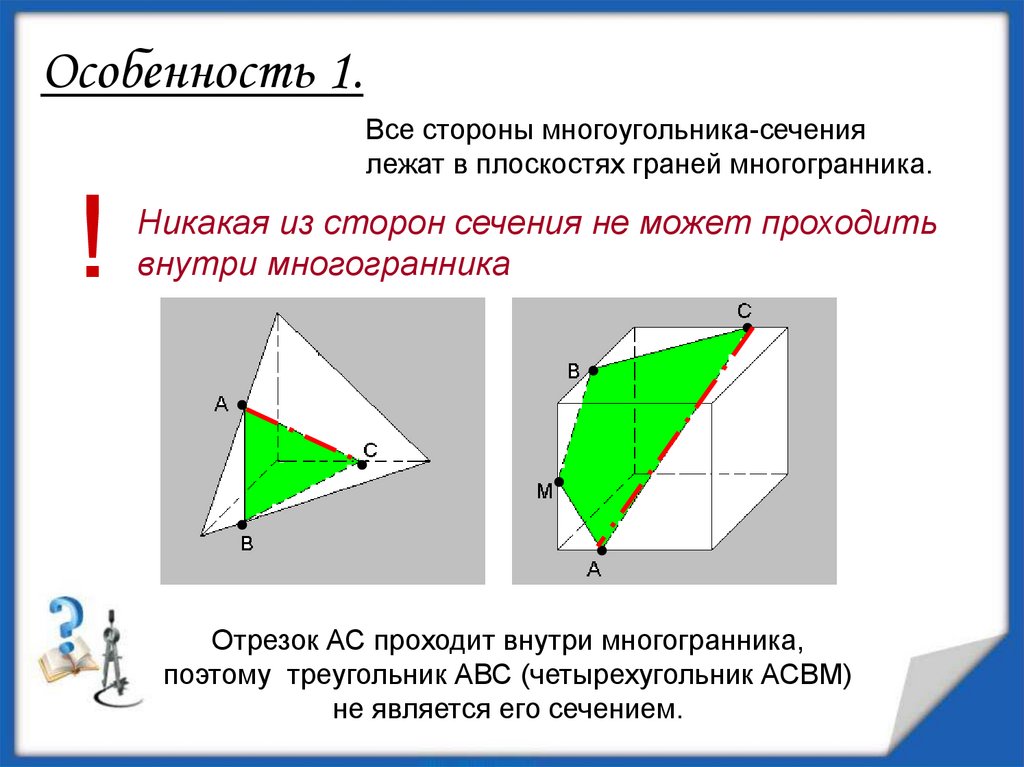
Особенность 1.Все стороны многоугольника-сечения
лежат в плоскостях граней многогранника.
!
Никакая из сторон сечения не может проходить
внутри многогранника
Отрезок АС проходит внутри многогранника,
поэтому треугольник АВС (четырехугольник АСВМ)
не является его сечением.
8.
Особенность 2.(Следует из аксиомы о пересечение двух плоскостей)
Каждую грань многогранника сечение может
пересекать не более, чем по одной прямой.
или
Ни одну из граней многогранника сечение не
может пересекать по двум (трем и т.д.) прямым.
АВСМК не является сечением
параллелепипеда, т.к. две его
стороны, АВ и ВС, лежат на
передней грани,
а, как известно, все общие точки
двух плоскостей лежат на
единственной прямой – прямой их
пересечения.
9.
АВСМК не являетсясечением октаэдра, т.к.
две его стороны ВС и МК
лежат на одной его
грани.
!
Каждая грань многогранника
содержит не более одной
стороны сечения.
10.
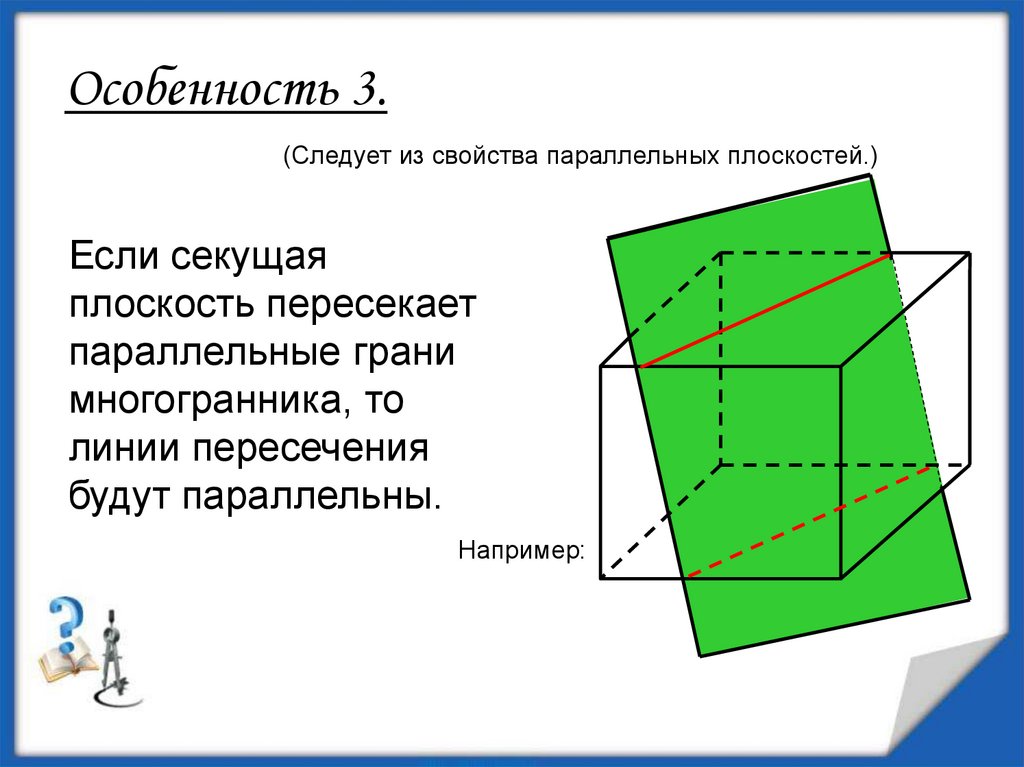
Особенность 3.(Следует из свойства параллельных плоскостей.)
Если секущая
плоскость пересекает
параллельные грани
многогранника, то
линии пересечения
будут параллельны.
Например:
11.
Итак:!
!
1. Никакая из сторон сечения
не может проходить внутри
многогранника
2. Каждая грань многогранника
содержит не более одной
стороны сечения.
!
3. Если секущая плоскость
пересекает параллельные
грани многогранника, то
линии пересечения будут
параллельны.
12.
3.Построение
сечений.
12
13.
Задачи напостроение
Часть первая –
само построение
и описание
построения.
Часть вторая –
доказательство того,
что построенный
многоугольник и есть
искомое сечение.
14.
В условиях задач на построение сечений обычно указывается несколькоточек, принадлежащих сечению и/или дополнительные условия,
которым должно соответствовать построенное сечение.
Данные точки могут лежать на
ребрах многогранника
и/или на его гранях
D
M
M
N
N
A
K
C
K
B
N принадлежит (ADB)
15.
Если соединив данные в условии точки, мы получиммногоугольник, все стороны которого будут лежать на гранях
многогранника, то сечение построено.
D
1.M (ADC) , N (ADC) =>
MN ( ADC )
2 M
(ADB), K
(ADB) =>
MK ( ADB )
M
N
A
C
K
B
3. K
(BDC), N
(BDC) =>
KN (BDC )
(MNK) – искомое сечение.
Но это может произойти только тогда, когда
каждые две соединяемые нами точки лежат в
одной грани.
16.
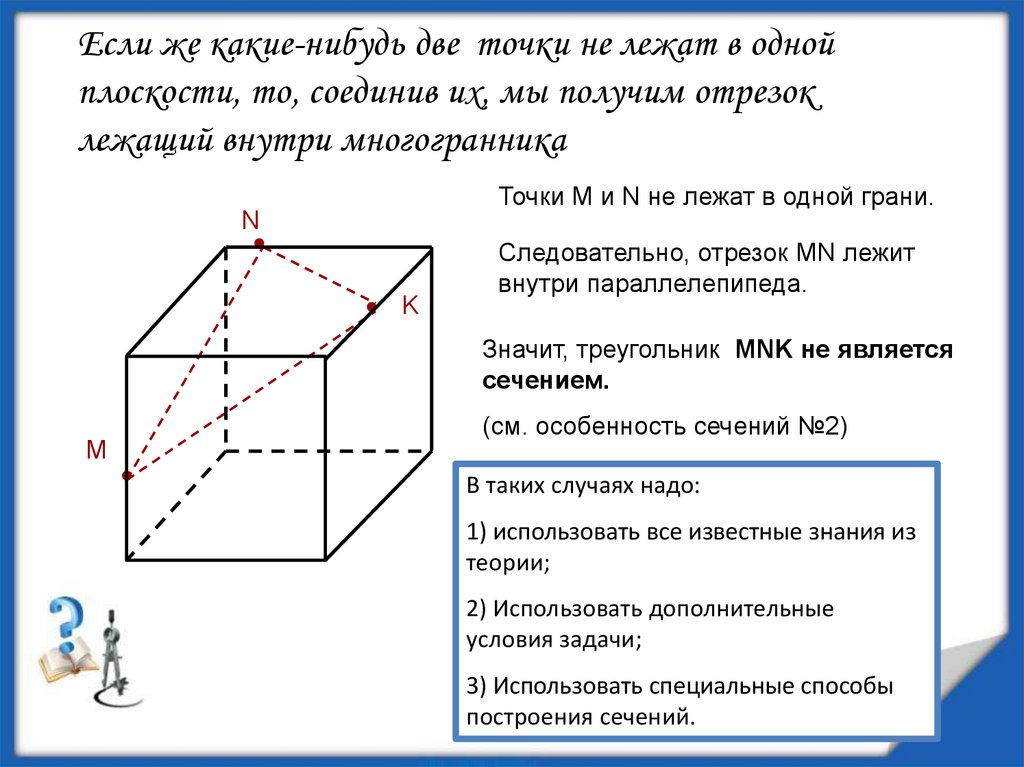
Если же какие-нибудь две точки не лежат в однойплоскости, то, соединив их, мы получим отрезок
лежащий внутри многогранника
Точки М и N не лежат в одной грани.
N
K
Следовательно, отрезок МN лежит
внутри параллелепипеда.
Значит, треугольник MNK не является
сечением.
(см. особенность сечений №2)
M
В таких случаях надо:
1) использовать все известные знания из
теории;
2) Использовать дополнительные
условия задачи;
3) Использовать специальные способы
построения сечений.
17.
Построить сечение,проходящее через точки
M, N, K
B1
N
C1
K
В этом случае мы
должны вспомнить, что
противоположные грани
параллелепипеда
параллельны.
Следовательно, секущая
плоскость пересечет их
по параллельным
прямым (особенность
сечений №3).
A1
M
D1
B
C
A
D
18.
В1N
Построение.
С1
1. N (BB1C1), K (BB1C1)
=> NK (BB1C1)
K
А1
D1
M
В
А
С
D
2. (BB1C1) || (AA1D1)
следовательно линии
пересечения секущей
плоскости с этими гранями
будут параллельны.
Секущая плоскость пересекает
(BB1C1) по прямой NK и имеет с
плоскостью (AA1D1) общую точку
M.
Следовательно, надо в плоскости (AA1D1) через
точку М провести прямую, параллельную NK.
19.
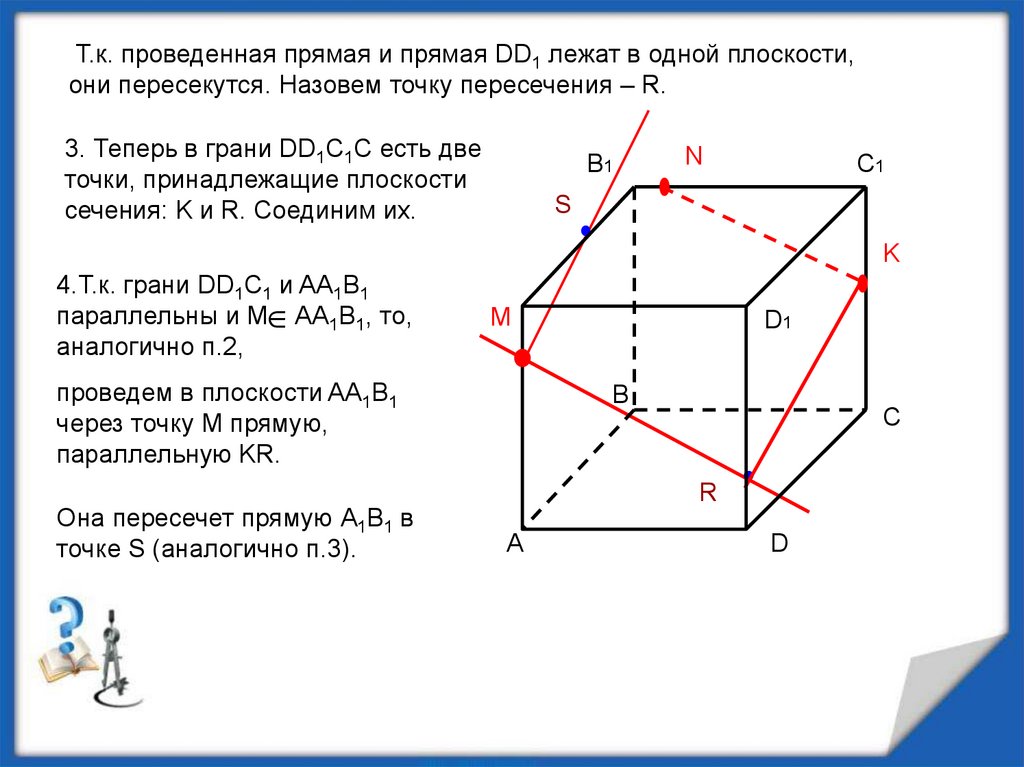
Т.к. проведенная прямая и прямая DD1 лежат в одной плоскости,они пересекутся. Назовем точку пересечения – R.
3. Теперь в грани DD1C1С есть две
точки, принадлежащие плоскости
сечения: K и R. Соединим их.
В1
N
С1
S
K
4.Т.к. грани DD1C1 и AA1B1
параллельны и М AA1B1, то,
аналогично п.2,
M
проведем в плоскости AA1B1
через точку М прямую,
параллельную KR.
Она пересечет прямую А1B1 в
точке S (аналогично п.3).
D1
В
С
R
А
D
20.
Теперь в верхней грани A1B1C1D1есть две точки сечения: S и N.
Соединим их.
В1
N
С1
S
K
M
D1
В
С
R
А
D
MRKNS – искомое
сечение
21.
Оформлениерешения задач.
22.
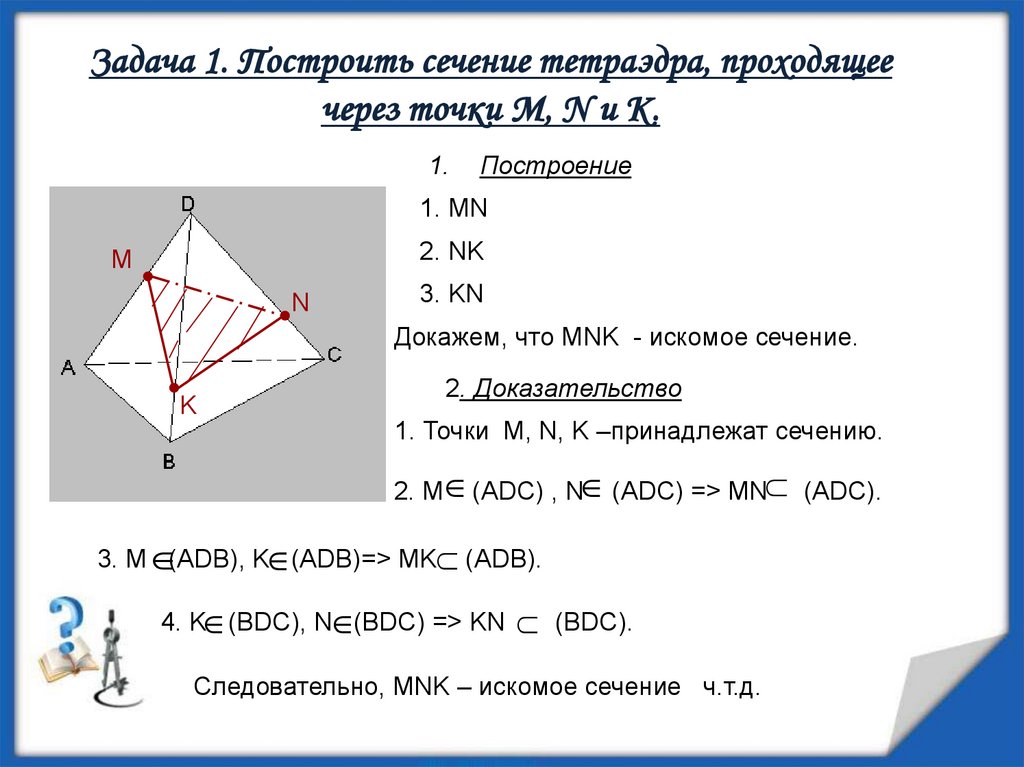
Задача 1. Построить сечение тетраэдра, проходящеечерез точки M, N и K.
1.
Построение
1. MN
2. NK
M
N
3. KN
Докажем, что MNK - искомое сечение.
K
2. Доказательство
1. Точки M, N, K –принадлежат сечению.
2. M (ADC) , N (ADC) => MN (ADC).
3. M (ADB), K (ADB)=> MK (ADB).
4. K (BDC), N (BDC) => KN
(BDC).
Следовательно, MNK – искомое сечение ч.т.д.
23.
Задача 2. Построить сечение параллелограмма,проходящее через точки M, N и K.
1.
B1
Построение
1. NK
N
C1
S
A1
K
2. В плоскости AA1D MR II NK,
MR∩ DD1=R
D1
3. RK
M
B
C
4. В плоскости AA1B1 MS II RK,
A
R
D
MS ∩ A1B1=S
5. SN
Докажем, что MRKNS – искомое сечение.
24.
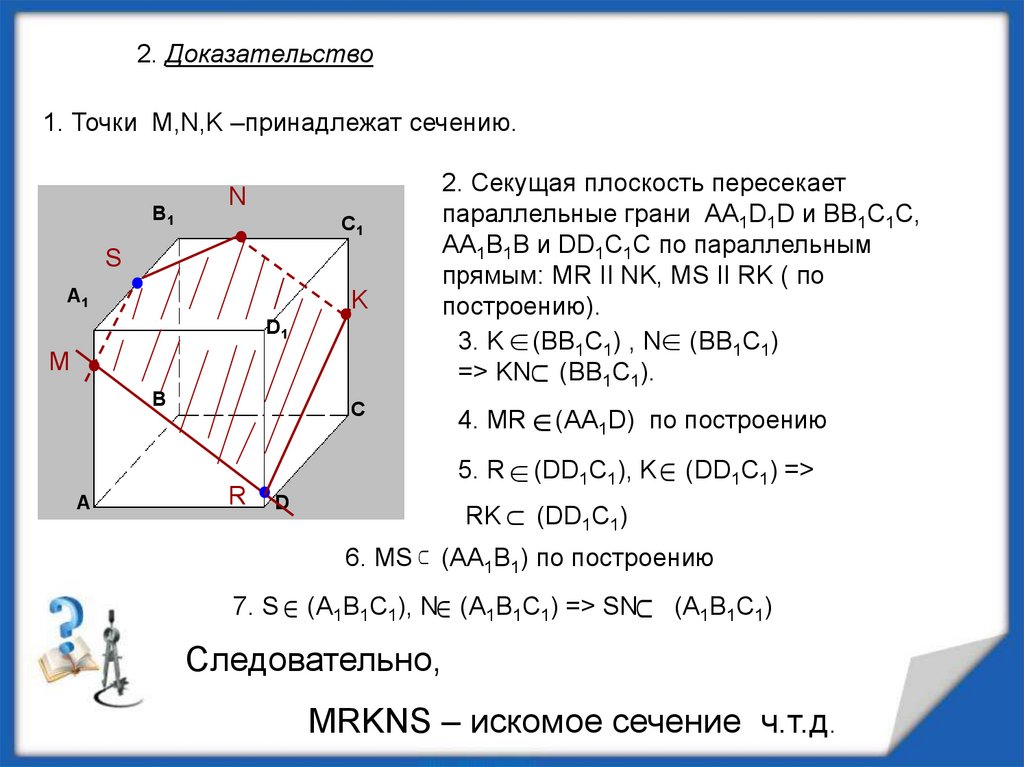
2. Доказательство1. Точки M,N,K –принадлежат сечению.
B1
N
C1
S
A1
K
D1
M
B
A
C
R
2. Секущая плоскость пересекает
параллельные грани AA1D1D и BB1C1C,
AA1B1B и DD1C1C по параллельным
прямым: MR II NK, MS II RK ( по
построению).
3. K (BB1C1) , N (BB1C1)
=> KN (BB1C1).
4. MR (AA1D) по построению
5. R (DD1C1), K (DD1C1) =>
RK (DD1C1)
D
6. MS (AA1B1) по построению
7. S (A1B1C1), N (A1B1C1) => SN (A1B1C1)
Следовательно,
MRKNS – искомое сечение ч.т.д.
25.
Задача 3. Построить сечение тетраэдра, проходящеечерез точки R, S и P, P (ABD).
1.
Построение
1. SR
2. SP, SP∩ AD = V
V
R
P
3. VR
Докажем, что RSV - искомое сечение.
2. Доказательство
S
1. Точки R, S, P принадлежат сечению.
2. S (BDC) , R (BDC) => SR (BDC).
3. S (ADB), P (ADB)=> PS (ADB), V (ADB)
4. V (ADC), R (ADC) => VR (ADC).
Следовательно, RSV – искомое сечение ч.т.д.
26.
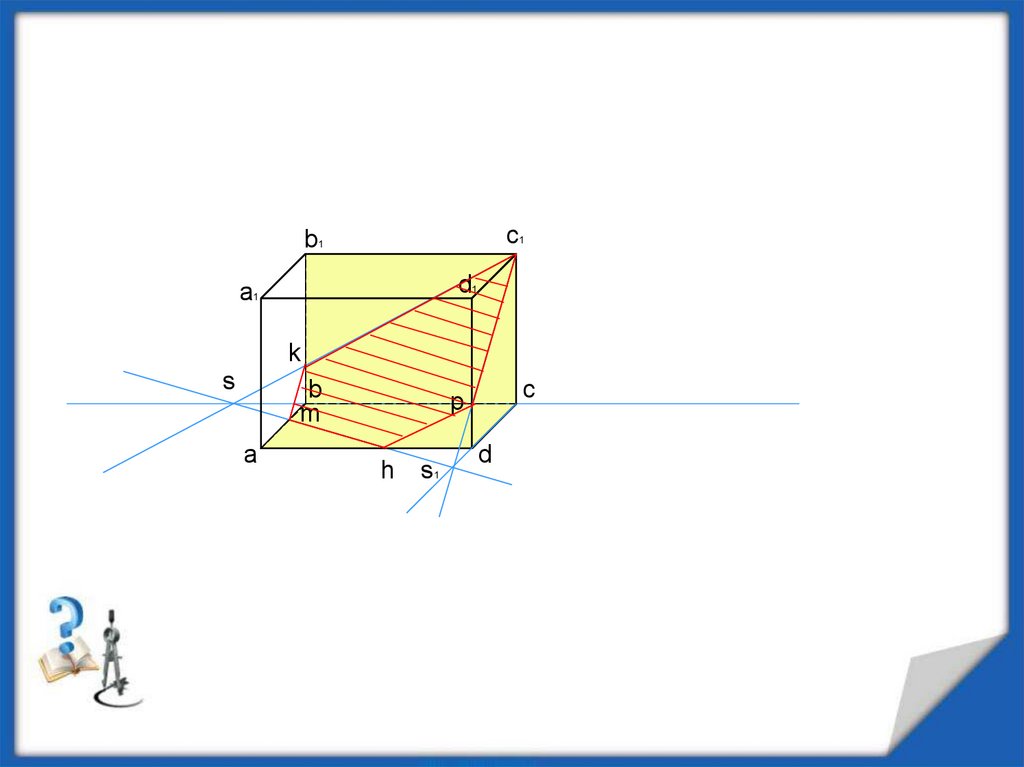
Задачи.26
27.
cb
1
1
d
a
1
1
k
s
b
m
a
c
p
h
d
s
1



















 Математика
Математика








