Похожие презентации:
Площадь сферы и объем шара
1. Площадь сферы и объем шара.
xО
2. Задание В13 ЕГЭ по математике
Тип заданий покодификатору
требований
Стереометрическая задача на нахождение
геометрических величин (длин, углов,
площадей, объемов)
Характеристика
задания
Несложное задание на вычисление элементов,
площадей поверхностей или объемов
многогранников или тел вращения.
Комментарий
Для решения задачи достаточно знать
свойства правильных пирамид и призм,
формулы площадей поверхности и объемов
пирамиды, призмы, цилиндра, конуса и шара.
3. Сфера
RО
Сферой называется
поверхность, состоящая
из всех точек
пространства,
расположенных на
данном расстоянии от
данной точки
Центром сферы является
данная точка, в данном
случаи точка О.
Радиусом сферы является
любой отрезок,
соединяющий центр и
какую-нибудь точку
сферы.
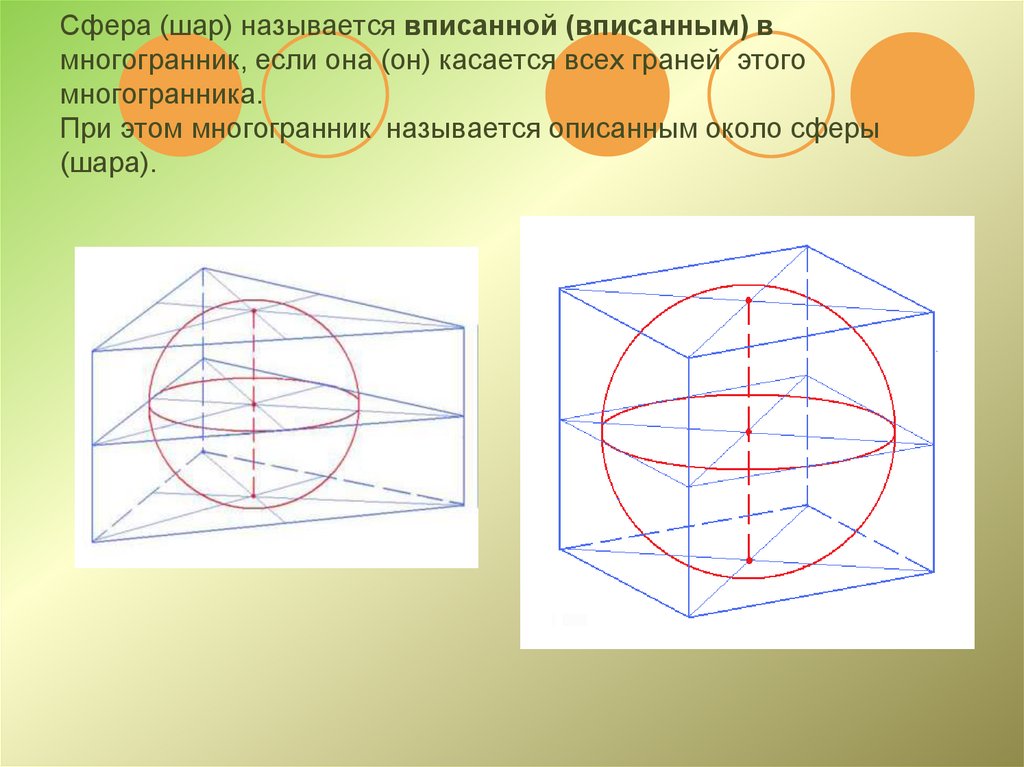
4. Сфера (шар) называется вписанной (вписанным) в многогранник, если она (он) касается всех граней этого многогранника. При этом
многогранник называется описанным около сферы(шара).
5. Шар
Шаром называется тело,ограниченное сферой.
Центр, радиус и диаметр
сферы являются так же
центром, радиусом и
диаметром шара,
где О – центр шара
Сечением шара плоскостью,
является круг.
6. Формулы для вычисления объема шара и площади сферы
Площадь сферы равна:S = 4 πR2 ,
где R – это радиус сферы
Объем шара равен:
V = 4/3πR3
где R – это радиус шара
7. Время вспомнить о ЕГЭ.
8. Решение тренировочных упражнений
№1. Объем одного шара в 27 разбольше объема второго. Во сколько раз
площадь поверхности первого шара
больше площади поверхности второго?
Ответ: в 9 раз
9. Решение тренировочных упражнений
№2. В куб с ребром 3 вписан шар.Найдите объем этого шара, деленный
на П.
Ответ: 4,5
10. Решение тренировочных упражнений
№3. Радиусы трех шаров равны3, 4 и 5. Найдите радиус шара, объем
которого равен сумме их объемов.
Ответ: 6
11. Решение тренировочных упражнений
№4. Сколько нужно взять шароврадиуса 2 см, чтобы сумма их объемов
равнялась объему шара радиуса 6 см?
Ответ: 27
12. Решение тренировочных упражнений
№5.Около конуса описана сфера (сферасодержит окружность основания
конуса и его вершину) Центр сферы
совпадает с центром основания конуса.
Найдите радиус сферы,
если образующая конуса
равна 80
Ответ:80
13. Решение тренировочных упражнений
№6 Дан шар с центром в точке О и двакруга с площадями 12 и 16,
образованные сечениями шара
параллельными плоскостями. Точка О
является центром большего из кругов,
на окружности меньшего из кругов
взяли точку А. Найдите угол между
прямой ОА и плоскостью, содержащей
больший круг.
14. Решение тренировочных упражнений
№7. На шаровой поверхности лежат всевершины треугольника АВС. Точка О
– центр шара. Найдите угол между
прямой АО и плоскостью
треугольника, если АВ=АС=10, ВС=12,
АО=12,5.
15. Решение тренировочных упражнений
№8. Диаметр шара равен 4. Через конецдиаметра проведена плоскость под
углом 30° к нему. Найдите площадь
сечения шара этой плоскостью.
16. Домашнее задание: Повторение теоретического материала по теме «Прямоугольный параллелепипед».
Решение прототипов В9 открытогобанка заданий ЕГЭ по математике.
Нахождение длин и площадей в
прямоугольном параллелепипеде.

















 Математика
Математика








