Похожие презентации:
Объем шара и площадь сферы
1.
2. Объем шара и площадь сферы
xО
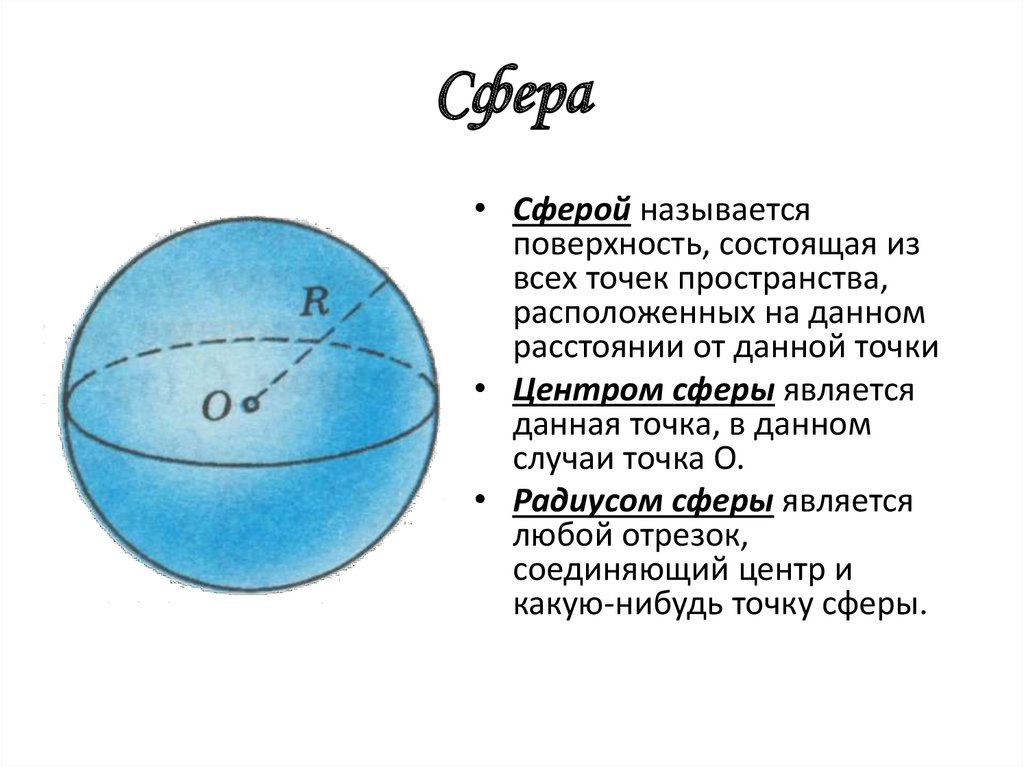
3. Сфера
• Сферой называетсяповерхность, состоящая из
всех точек пространства,
расположенных на данном
расстоянии от данной точки
• Центром сферы является
данная точка, в данном
случаи точка О.
• Радиусом сферы является
любой отрезок,
соединяющий центр и
какую-нибудь точку сферы.
4. Круговой сектор
Круговым сектором илипросто сектором
называется часть круга,
ограниченная дугой и
двумя радиусами,
соединяющими концы
дуги с центром круга.
Дуга, которая
ограничивает сектор,
называется дугой сектора.
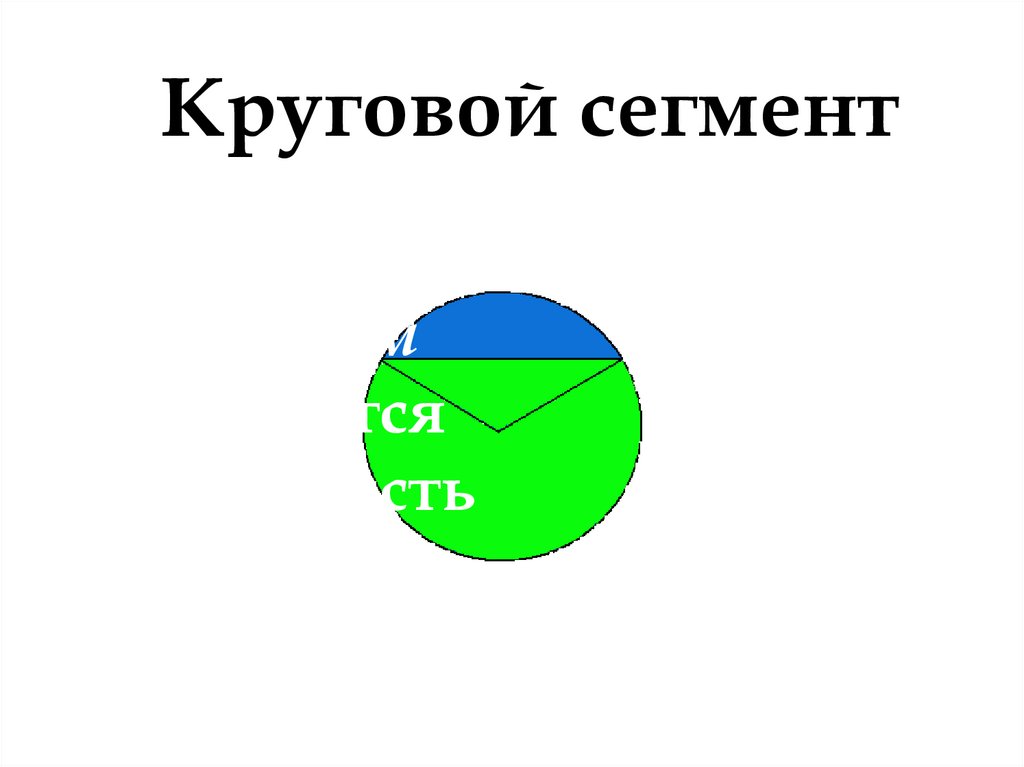
5. Круговой сегмент
Круговымсегментом
называется
общая часть
круга и
полуплоскос
ти
6. Шаровой слой
• Шаровым слоем называетсячасть шара, заключенная между
двумя параллельными
секущими плоскостями.
• Основаниями шарового слоя
являются круги, получившиеся в
сечении шара этими
плоскостями.
• Высотой шарового слоя
является расстояние между
плоскостями.
7. Шаровой сектор
• Шаровым сектором называетсятело, полученное вращением
кругового сектора с углом,
меньшим 90° , вокруг прямой,
содержащей один из
ограничивающих круговой сектор
радиусов.
• Шаровой сектор состоит из
шарового сегмента и конуса, где R
– это радиус шара.
• Высотой шарового сектора
является высота шарового
сегмента и она равна h.
8. Формулы для вычисления объема: шара, шарового сектора, шарового слоя, шарового сектора и площади сферы
Площадь сферы равна:
S = 4πR2 ,
где R – это радиус сферы
Объем шара равен:
V = 1⅓πR3 = 4/3πR3
где R – это радиус шара
Объем шарового сегмента равен:
V =πh2( R - ⅓h) ,
где R – это радиус шара, а h – это высота сегмента
Объем шарового слоя равен:
V = V1 – V2 ,
где V1 – это объем одного шарового сегмента, а V2 – это объем второго шарового сегмента
Объем шарового сектора равен:
V = ⅔πR2h ,
где R – это радиус шара, а h – это высота шарового сегмента
9. Разобрать задачи
10.
11. З
12. Выполните задания.
1. Куб вписан в шаррадиуса 8√3 .
Найдите объем
куба.
2. Конус вписан в
шар. Радиус
основания конуса
равен радиусу
шара. Объем
конуса равен 45.
Найдите объем
шара.
13. Задачу № 4 решите, введением системы координат.( на оценку 5, всем можно не решать)
3. Середина ребра куба 4.Длина диагонали куба ABCDA1B1C1D1
со стороной 1,8
равна 3. На луче A1C
является центром
отмечена точка P
шара радиуса 0,8.
так, что A1P = 4.
Найдите
а)
Докажите,
что
площадь S части
PBDC1 —
поверхности шара,
правильный тетраэд
лежащей внутри
р.
куба. В ответе
• б) Найдите длину отр
запишите S/π .
езка AP.











 Математика
Математика








