Похожие презентации:
Углы и отрезки, связанные с окружностью. 10 класс
1.
Учитель математики Папулина О.В.2.
3.
Образовательные :Рассмотреть все возможные комбинации углов и отрезков, связанных с
окружностью (углы между: касательной и хордой; двумя
пересекающимися хордами; двумя секущими, проведенными из одной
точки; касательной и секущей, проведенными из одной точки; двумя
касательными, проведенными с одной точки); формировать навык
чтения чертежей.
Развивающие:
Развить воображение учащихся при решении геометрических задач,
геометрическое мышление, интерес к предмету, математическую речь,
память, внимание, умение делать выводы и обобщение.
Воспитательные:
Воспитывать у учащихся ответственное отношение к учебному труду,
формировать эмоциональную культуру и культуру общения, чувство
патриотизма, умение четко организовывать самостоятельную и
индивидуальную работу.
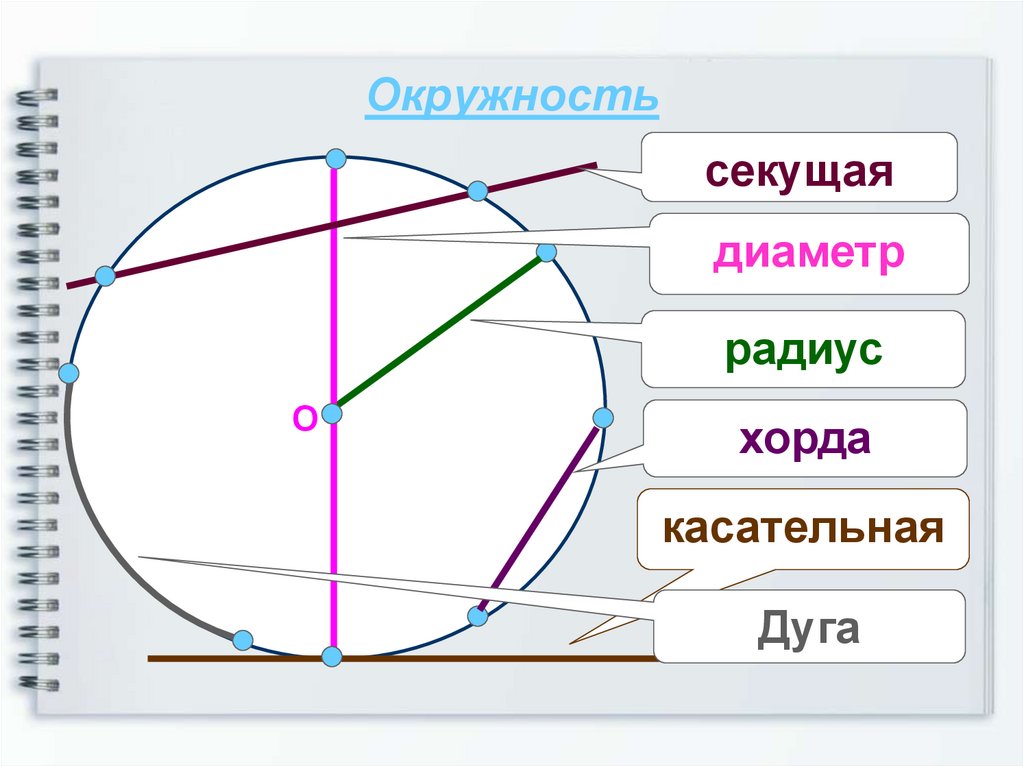
4. Окружность
секущаядиаметр
радиус
О
хорда
касательная
Дуга
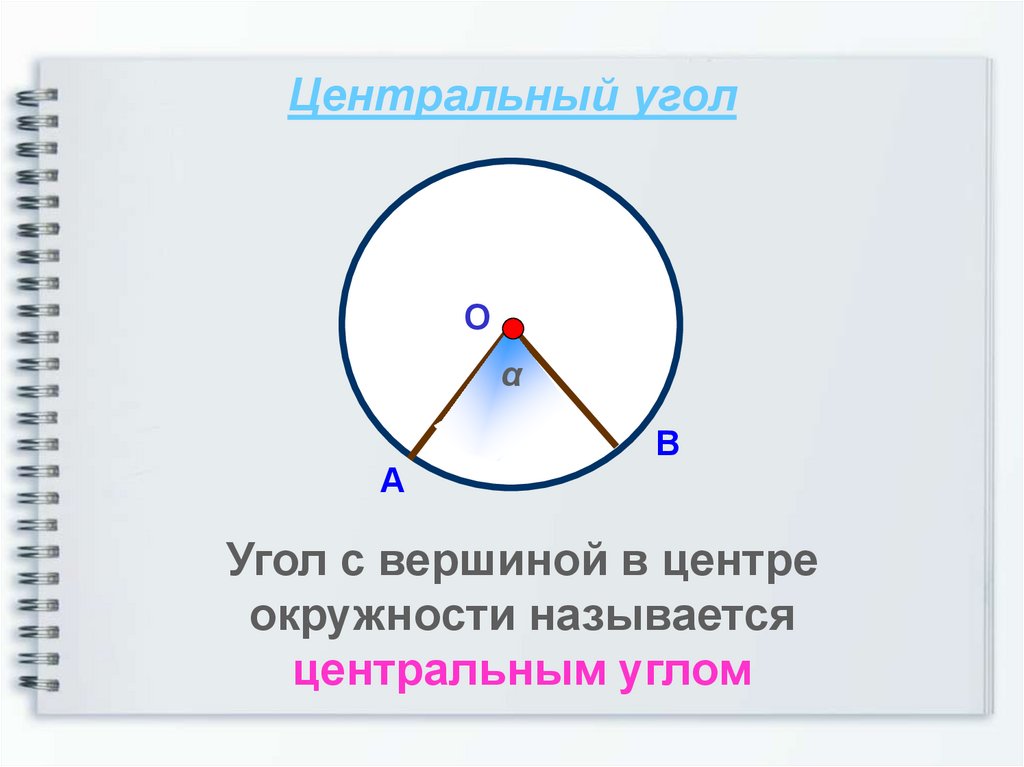
5. Центральный угол
Оα
А
В
Угол с вершиной в центре
окружности называется
центральным углом
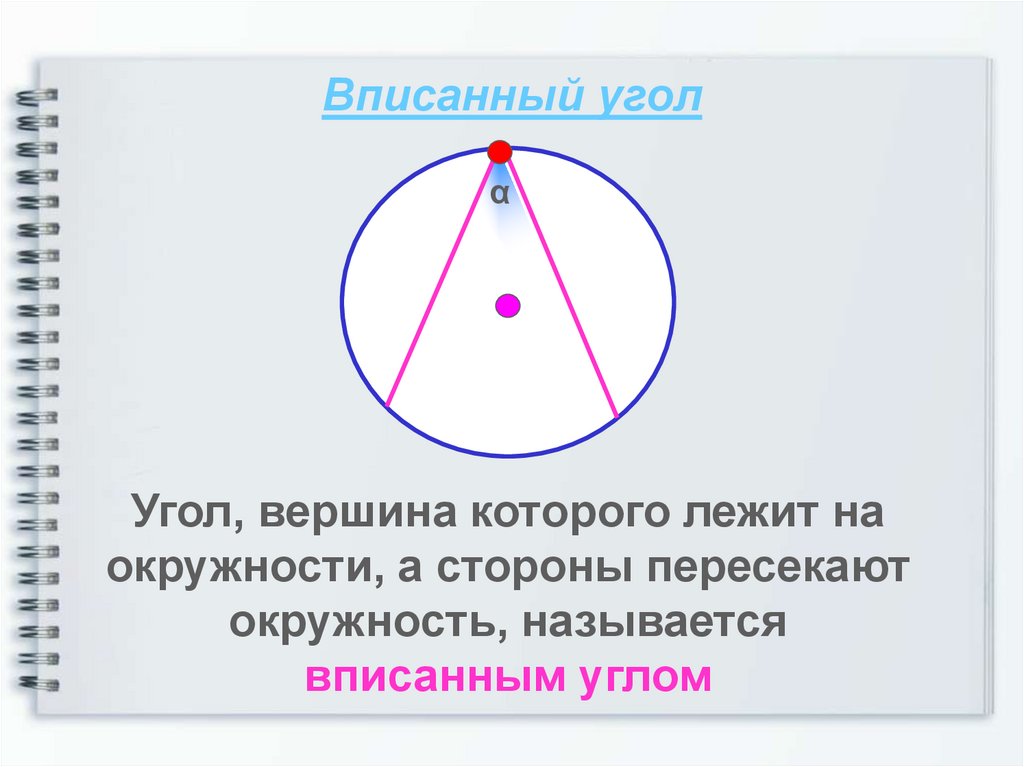
6. Вписанный угол
αУгол, вершина которого лежит на
окружности, а стороны пересекают
окружность, называется
вписанным углом
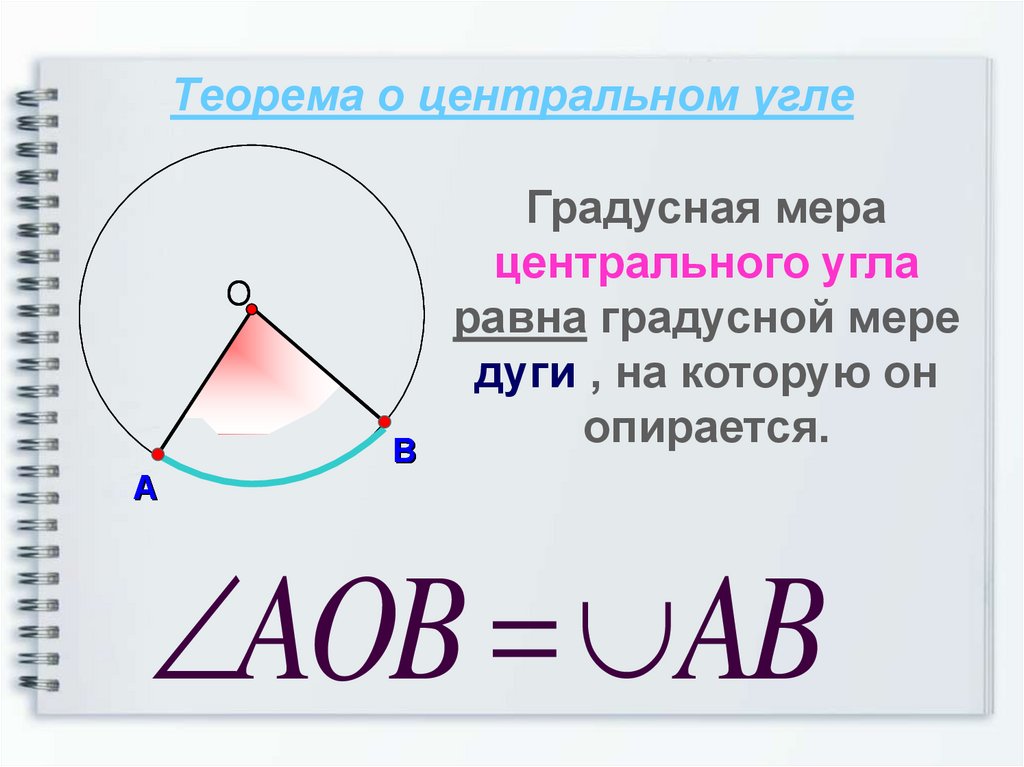
7. Теорема о центральном угле
ОА
В
Градусная мера
центрального угла
равна градусной мере
дуги , на которую он
опирается.
AOB AB
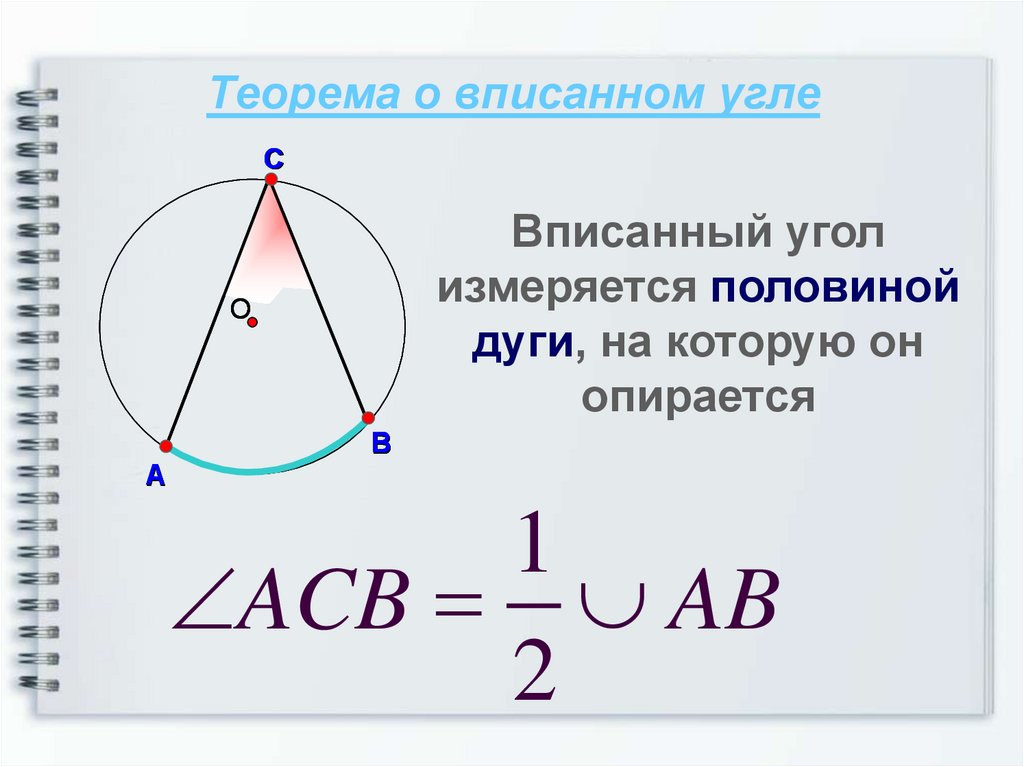
8. Теорема о вписанном угле
СВписанный угол
измеряется половиной
дуги, на которую он
опирается
О
А
В
1
ACB AB
2
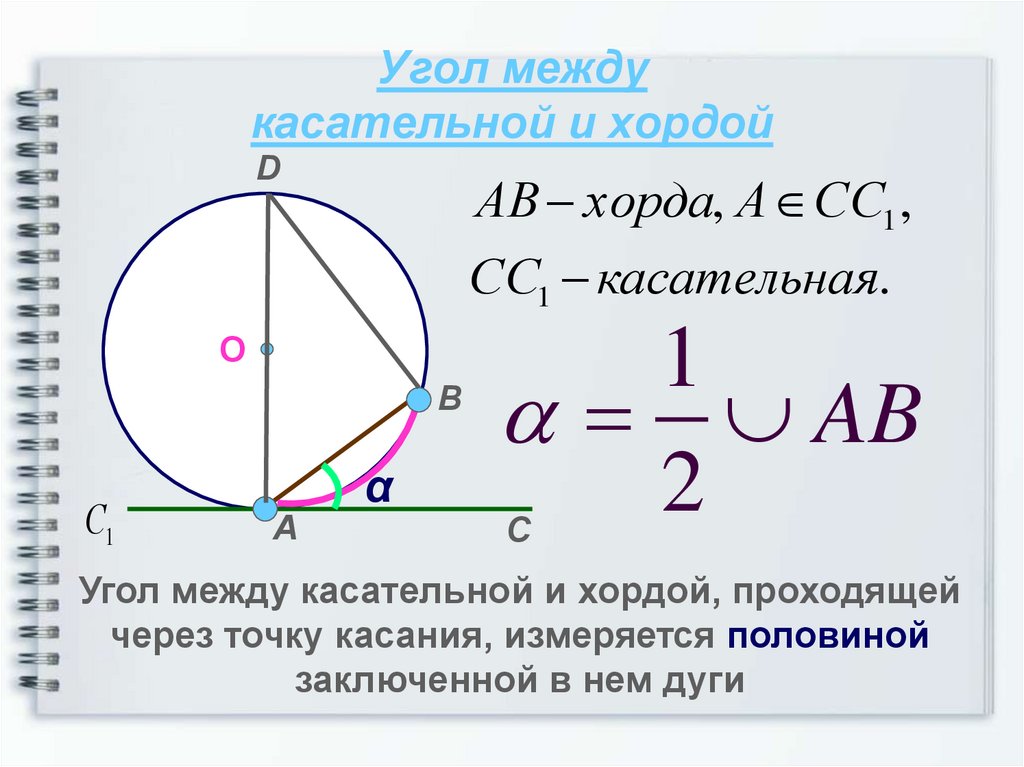
9. Угол между касательной и хордой
DАВ хорда, А СС1 ,
СС1 касательная.
О
В
С1
А
α
1
AB
2
С
Угол между касательной и хордой, проходящей
через точку касания, измеряется половиной
заключенной в нем дуги
10. Теорема об отрезках пересекающихся хорд
СА
Е
В
AB, CD – хорды,
AB ∩ CD = E.
АЕ · ВЕ = СЕ ·DЕ
D
Произведение отрезков одной из двух
пересекающихся хорд равно
произведению отрезков другой хорды.
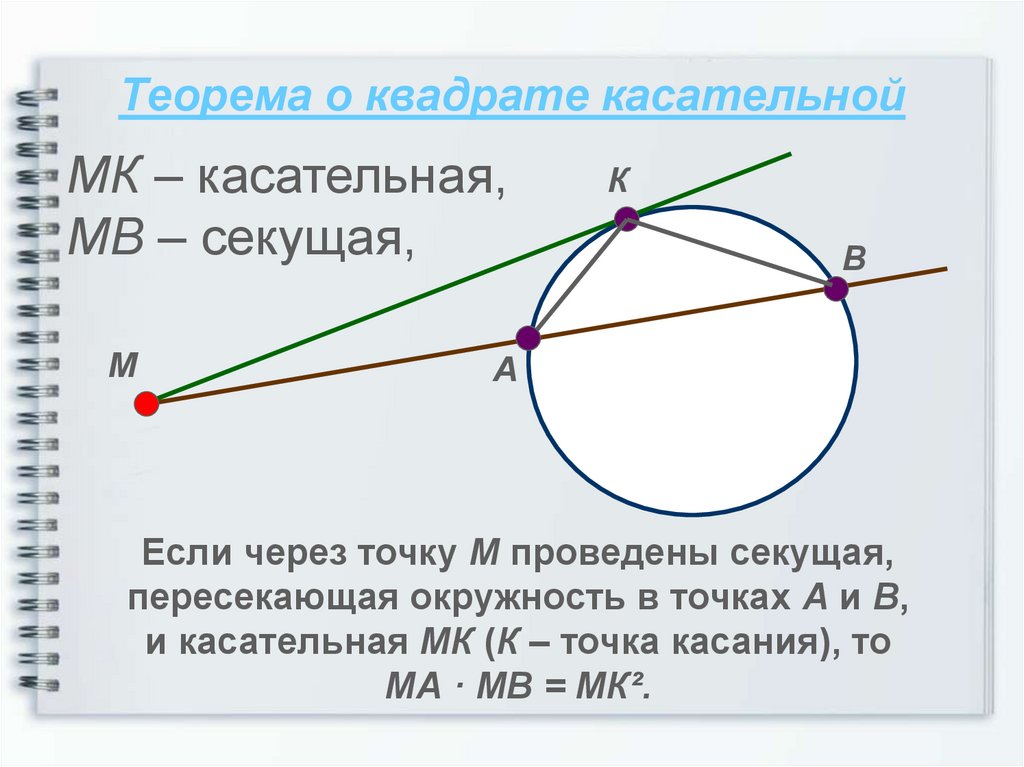
11. Теорема о квадрате касательной
МК – касательная,МВ – секущая,
М
К
В
А
Если через точку М проведены секущая,
пересекающая окружность в точках А и В,
и касательная МК (К – точка касания), то
МА · МВ = МК².
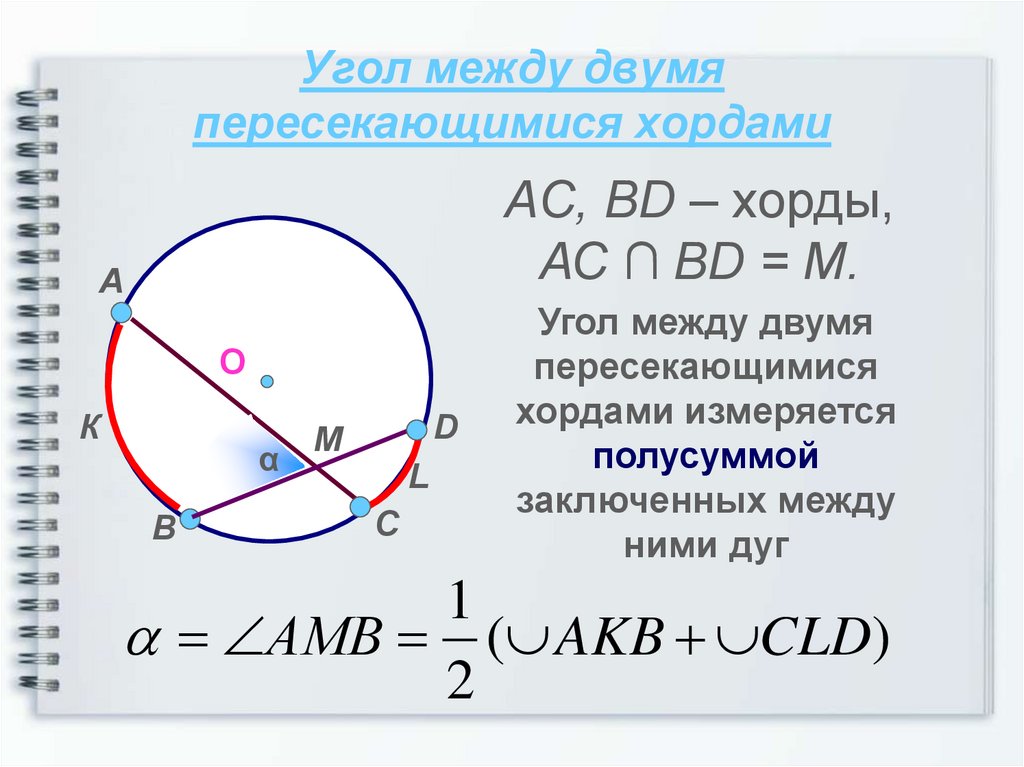
12. Угол между двумя пересекающимися хордами
AC, BD – хорды,АС ∩ BD = M.
А
О
К
α
В
D
М
L
C
Угол между двумя
пересекающимися
хордами измеряется
полусуммой
заключенных между
ними дуг
1
АМВ ( AKB CLD)
2
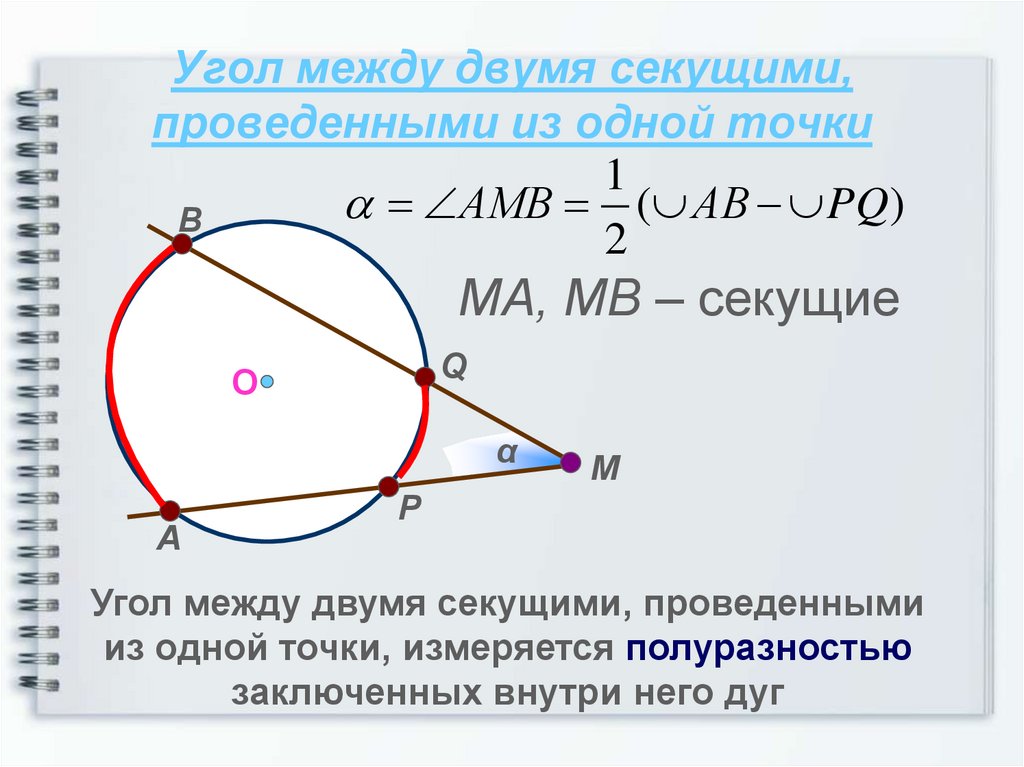
13. Угол между двумя секущими, проведенными из одной точки
1АМВ ( АВ PQ)
B
2
МА, МВ – секущие
Q
О
α
A
M
P
Угол между двумя секущими, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
14. Угол между касательной и секущей, проведенными из одной точки
1АМК ( АК ВК )
2
К
МК – касательная,
МА – секущая.
О
А
В
α
М
Угол между касательной и секущей, проведенными
из одной точки, измеряется полуразностью
заключенных внутри него дуг
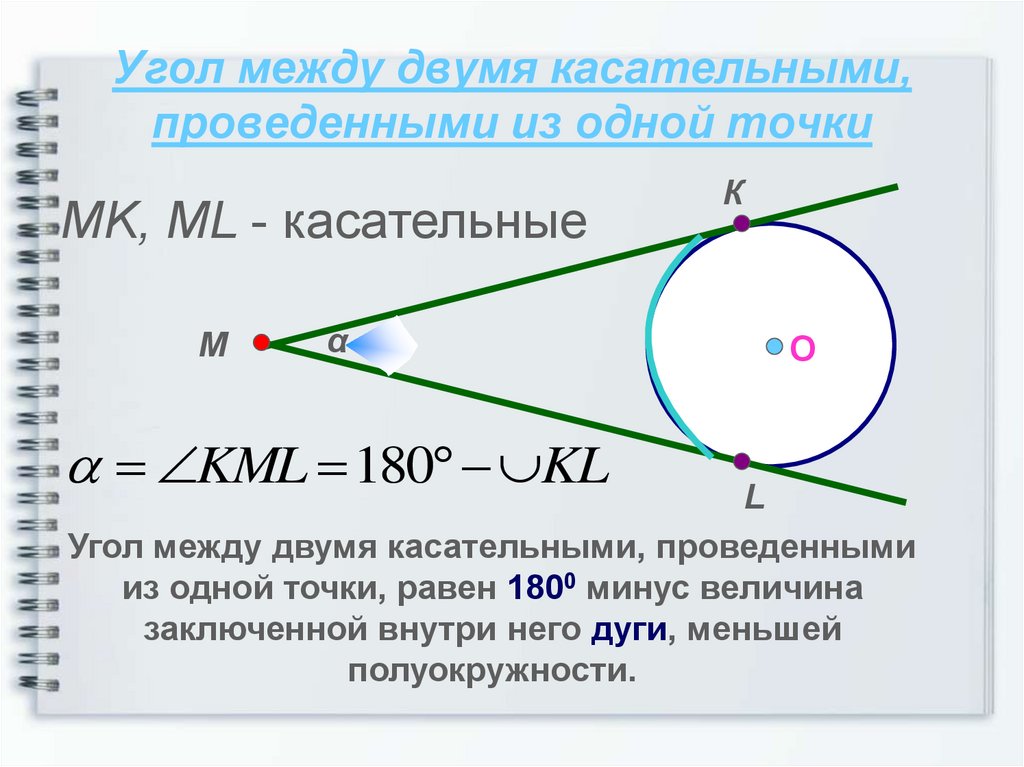
15. Угол между двумя касательными, проведенными из одной точки
MK, ML - касательныеМ
α
KML 180 KL
К
О
L
Угол между двумя касательными, проведенными
из одной точки, равен 1800 минус величина
заключенной внутри него дуги, меньшей
полуокружности.
16. Решение задач по готовым чертежам
1В
D
О
А
ACB : ADB 3: 5
Дано:
Найти:
С
BAE
Решение:
Е
1
1) BAE ACB
2
2) АСВ : ADB 3 : 5,
(по теореме об угле между
касательной и хордой)
3 5 8 частей
3
АСВ ADB 360 , АСВ 360 135 .
8
3)
1
ВАЕ 135 67,5 .
2
Ответ:
67,50
17.
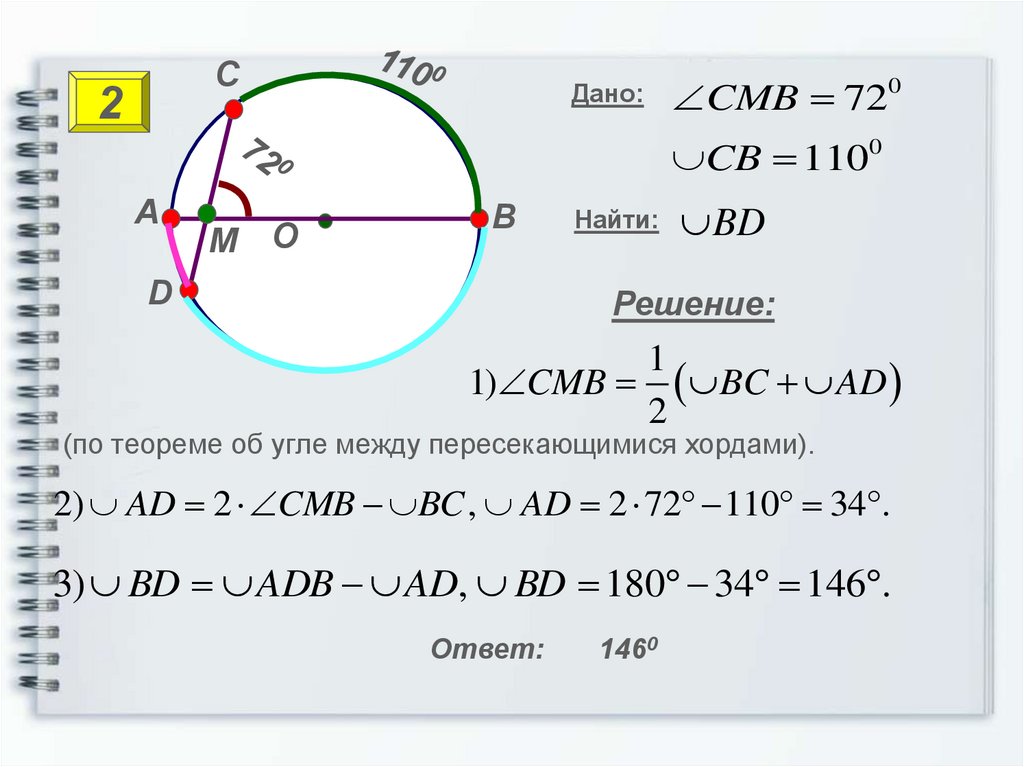
С2
Дано:
CMB 720
CB 1100
А
M
О
В
D
Найти:
BD
Решение:
1
1) CMB BC AD
2
(по теореме об угле между пересекающимися хордами).
2) AD 2 CMB BC , AD 2 72 110 34 .
3) BD ADB AD, BD 180 34 146 .
Ответ:
1460
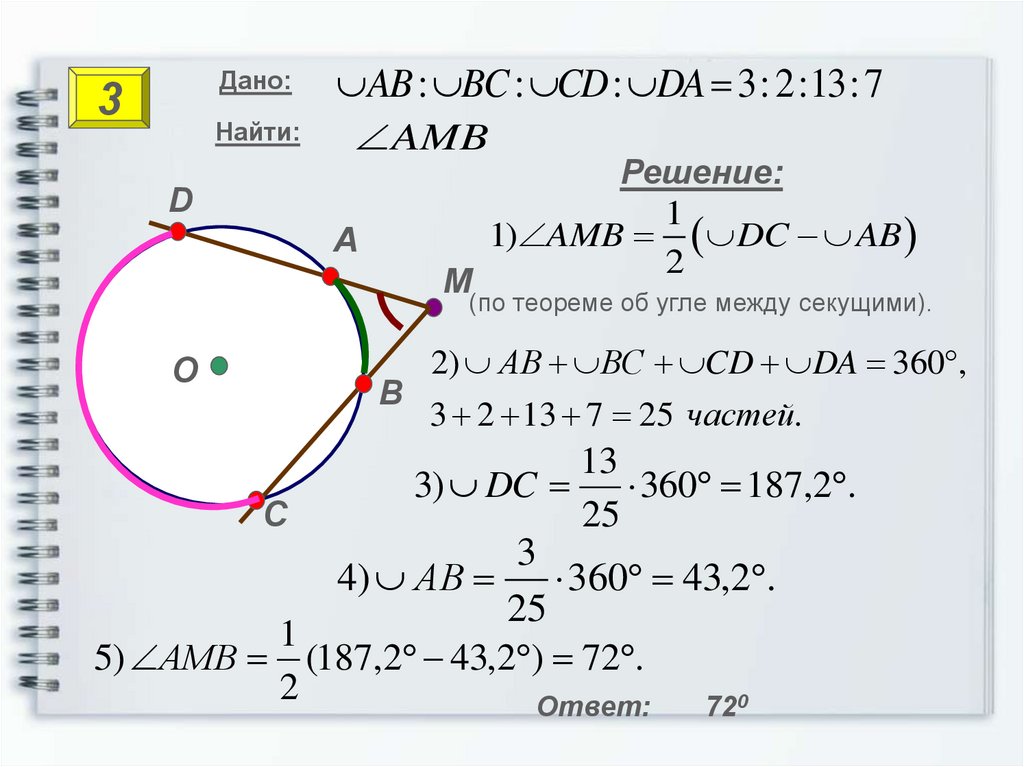
18.
Дано:3
Найти:
AB : BC : CD : DA 3: 2:13: 7
AMB
D
А
M
Решение:
1
1) AMB DC AB
2
(по теореме об угле между секущими).
О
B
2) АВ ВС CD DA 360 ,
3 2 13 7 25 частей.
13
3) DC 360 187,2 .
C
25
3
4) АВ
360 43,2 .
25
1
5) АМВ (187,2 43,2 ) 72 .
2
Ответ:
720
19.
4Дано: BDC 112 , BD : DC 7 : 9.
Найти:
BAD
Решение:
1
1) BAD DC DB
2
(по теореме об угле между касательной
и секущей).
2) BDC BD DC
A
7 9 16 частей.
9
9
3) DC BDC 112 63 .
16
16
7
7
4) DB BDC 112 49 .
16
16
1
5) BAD (63 49 ) 7 .
2
Ответ:
70
20.
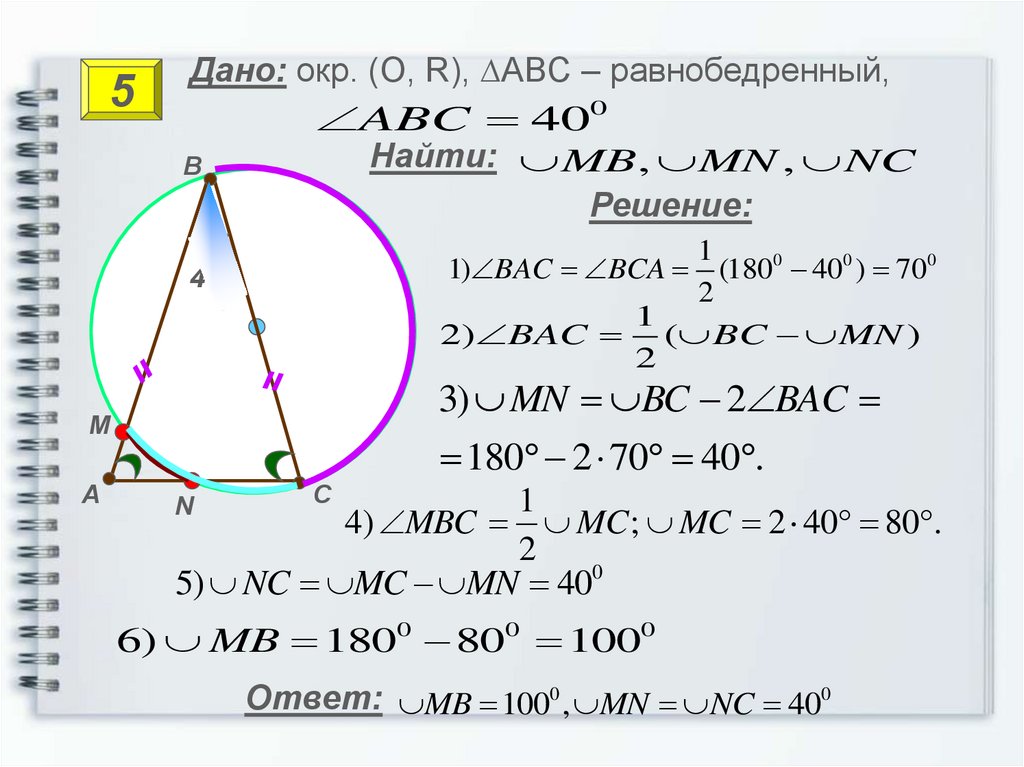
5Дано: окр. (О, R), ∆ABC – равнобедренный,
ABC 400
Найти: MB, MN , NC
B
Решение:
1
1) BAC BCA (1800 400 ) 700
2
1
2) BAC ( BC MN )
2
400
3) MN BC 2 BAC
M
A
180 2 70 40 .
C
1
4) MBC MC ; MC 2 40 80 .
2
5) NC MC MN 400
N
6) MB 1800 800 1000
Ответ: MB 1000 , MN NC 400
21. Решение задач по учебнику
№ 816 у доски№ 817 у доски
Дополнительно: № 821 у доски
Углы и отрезки, связанные с
окружностью.pptx
22. Итог урока
Закончи фразу1) Угол между касательной и хордой, проходящей
через точку касания, измеряется …
2) Произведение отрезков одной из двух
пересекающихся хорд равно …
3) Произведение секущей на её внешнюю часть
равно …
4) Угол между двумя пересекающимися хордами
измеряется …
5) Угол между двумя секущими, проведенными из
одной точки, измеряется …
6) Угол между касательной и секущей,
проведенными из одной точки, измеряется …
7) Угол между двумя касательными,
проведенными из одной точки, равен …
23. Домашнее задание
§ 1, пп. 85 – 87, стр. 187 – 190№ 818
№819
№ 820











 Математика
Математика








