Объём цилиндра

1. Объём цилиндра

Урок 34

2. Решение задач

№ 663 г

3.

Вопросы для повторения:
— Что называется цилиндром, осью цилиндра, высотой
цилиндра, радиусом цилиндра?
— Что является основанием цилиндра?
— Что является развёрткой боковой поверхности
цилиндра?

4.

Что называется цилиндром, осью цилиндра, высотой
цилиндра, радиусом цилиндра?
Цилиндр — тело, ограниченное цилиндрической
поверхностью и двумя кругами с границами O(r), O1(r)
Ось цилиндра — прямая OO1
Высота цилиндра — длина образующей
Радиус цилиндра — радиус основания
O1
O
r T
1
r
T

5.

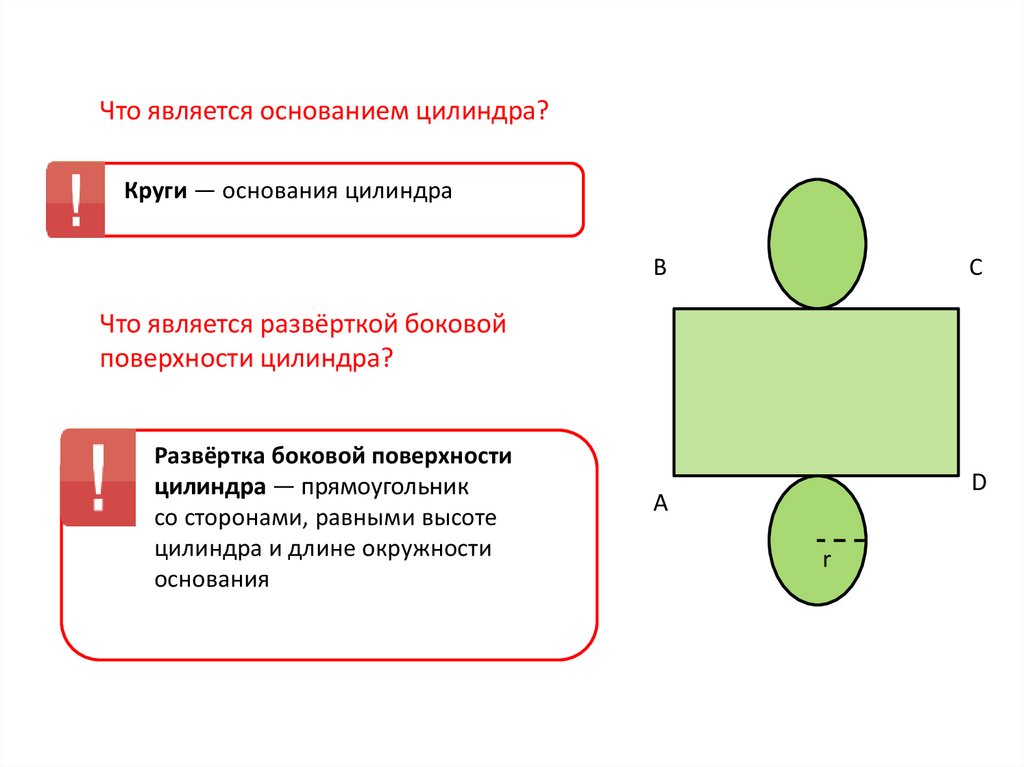
Что является основанием цилиндра?
Круги — основания цилиндра
B
C
Что является развёрткой боковой
поверхности цилиндра?
Развёртка боковой поверхности
цилиндра — прямоугольник
со сторонами, равными высоте
цилиндра и длине окружности
основания
D
A
r

6.

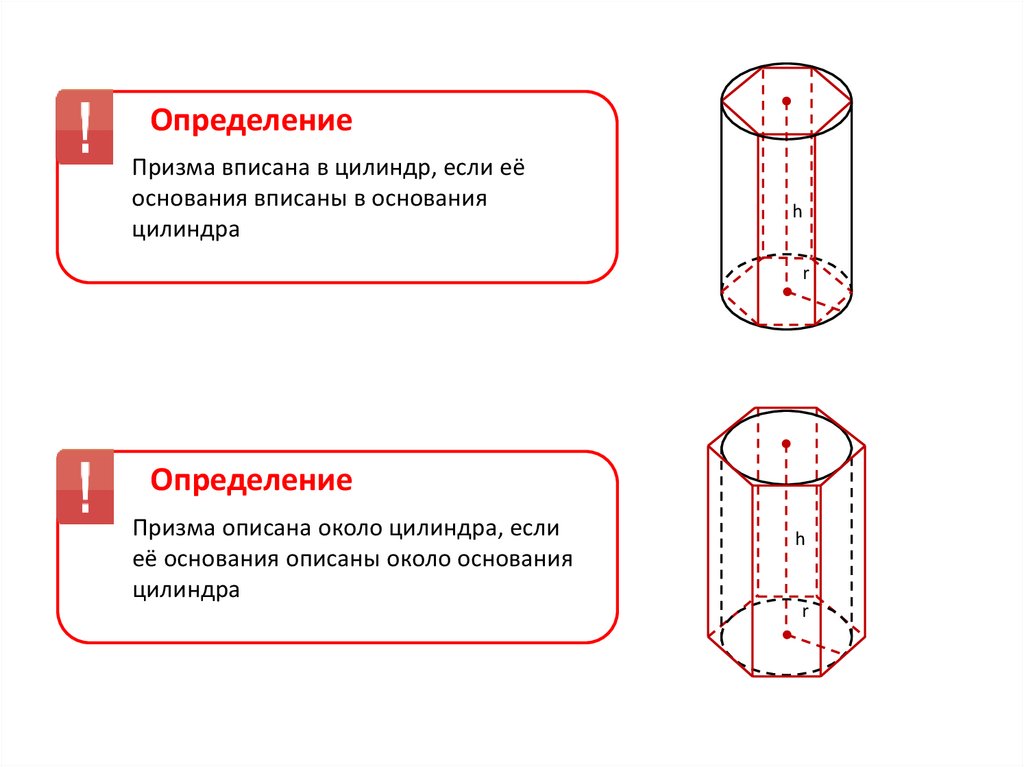
Определение
Призма вписана в цилиндр, если её
основания вписаны в основания
цилиндра
h
r
Определение
Призма описана около цилиндра, если
её основания описаны около основания
цилиндра
h
r

7.

Теорема
Объём цилиндра равен произведению
площади основания на высоту
V=
2
πr h

8.

Теорема
Объём цилиндра равен произведению площади основания
на высоту
Дано:
цилиндр P
n → ∞, rn → r ⇒ Vn → V
r — радиус, h — высота
limn →∞ Vn = V
Доказать: Vцил. = Sосн.· h
(1) ⇒ limn →∞ Sn · h = V
Доказательство:
Но limn →∞ Sn = πr2
Fn — n-угольная призма, вписанная в
цилиндр Р радиуса r и высотой h
Pn — цилиндр, rn — радиус
V = πr2h
Теорема доказана
h
Fn — описанная призма для Pn
V и Vn — объёмы цилиндров P и Pn
r
⇒ Vn < Sn · h < V
(1)

9. Решение упражнений

№ 666 (ав)

10.

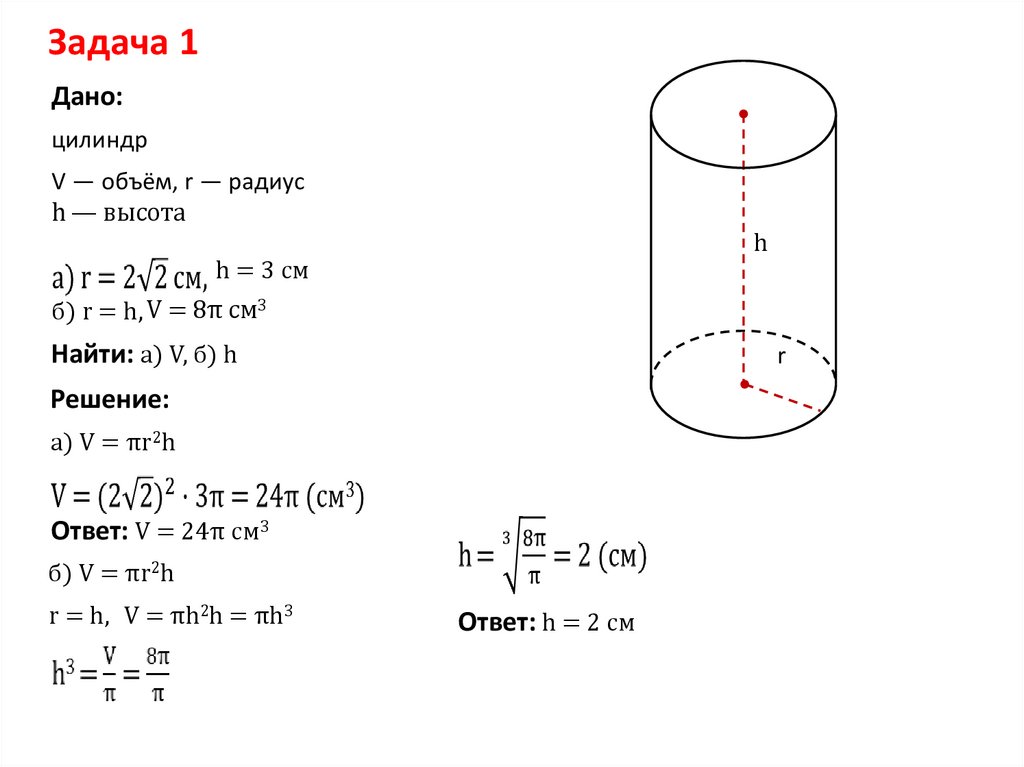
Задача 1
Дано:
цилиндр
V — объём, r — радиус
h — высота
h
h = 3 см
б) r = h, V = 8π см3
Найти: а) V, б) h
r
Решение:
a) V = πr2h
Ответ: V = 24π см3
б) V = πr2h
r = h, V = πh2h = πh3
Ответ: h = 2 см

11.

Задача 2
Дано:
цилиндры
h1 = 45 см
V1 = V2 — объём жидкости
d2 = 3d1
Найти: h2
Решение:
h1
V1 = V2
h2
V = πr2h
V1 = πr12 ∙ 45
V2 = πr22 ∙ h2
πr12 ∙ 45 = πr22 ∙ h2
d2 = 3d1, r2 = 3r1
r12 ∙ 45 = (3r1)2h2
r12 ∙ 45 = 9r12h2
h2 = 5 см
Ответ: h2 = 5 см
d1
d2

12.

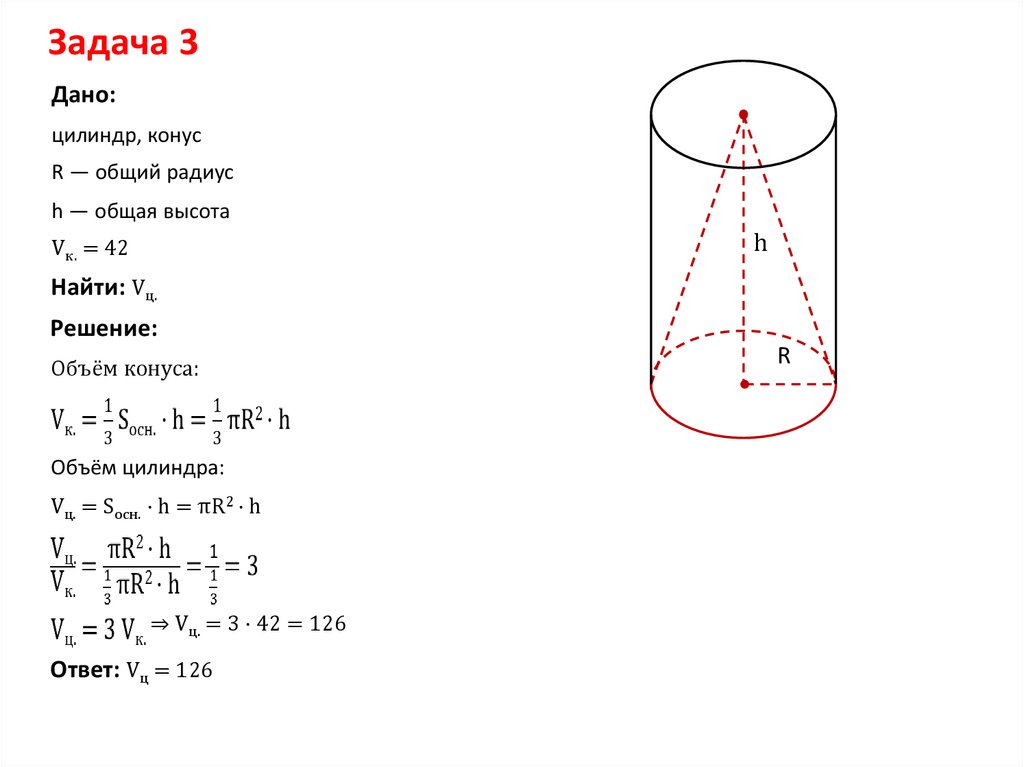
Задача 3
Дано:
цилиндр, конус
R — общий радиус
h — общая высота
h
Vк. = 42
Найти: Vц.
Решение:
Объём конуса:
Объём цилиндра:
Vц. = Sосн. · h = πR2 · h
⇒ Vц. = 3 · 42 = 126
Ответ: Vц = 126
R

13. Домашнее задание

• П.77
• № 666 б
• № 667