Похожие презентации:
Двугранный угол. Решение задач. Трехгранный угол
1.
Урок по геометрии в 10 классе разработанпо учебнику Л.С.Атанасяна.
Учитель Отдельнова Л.В.
2. Двугранный угол. Решение задач. Трехгранный угол.
3. Цель урока:
Сформировать у обучающихсяконструктивный подход по выработке умений
и навыков находить угол между плоскостями.
Познакомить обучающихся с понятием
многоугольного угла и трёхгранного угла,
примерами этих углов. Рассмотреть
ограничения на плоские углы многогранных
Заслушать отчёт исследовательской работы
по свойству линейных углов трёхгранного
угла.
4. Вид урока: изучение и первичное закрепление новых знаний
Оборудование: компьютер, проектор,слайды, диск “Открытая математика”,
модели многогранников, чертежные
инструменты, цветные мелки.
5.
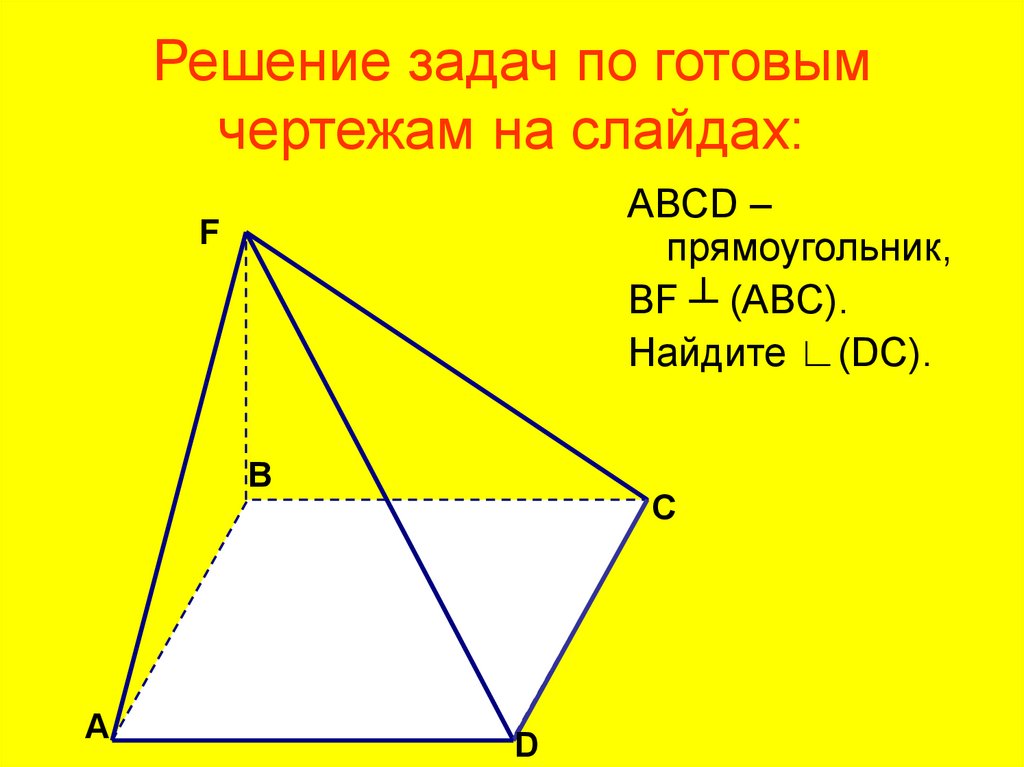
Решение задач по готовымчертежам на слайдах:
ABCD –
прямоугольник,
BF ┴ (ABC).
Найдите ∟(DC).
F
B
C
А
D
6.
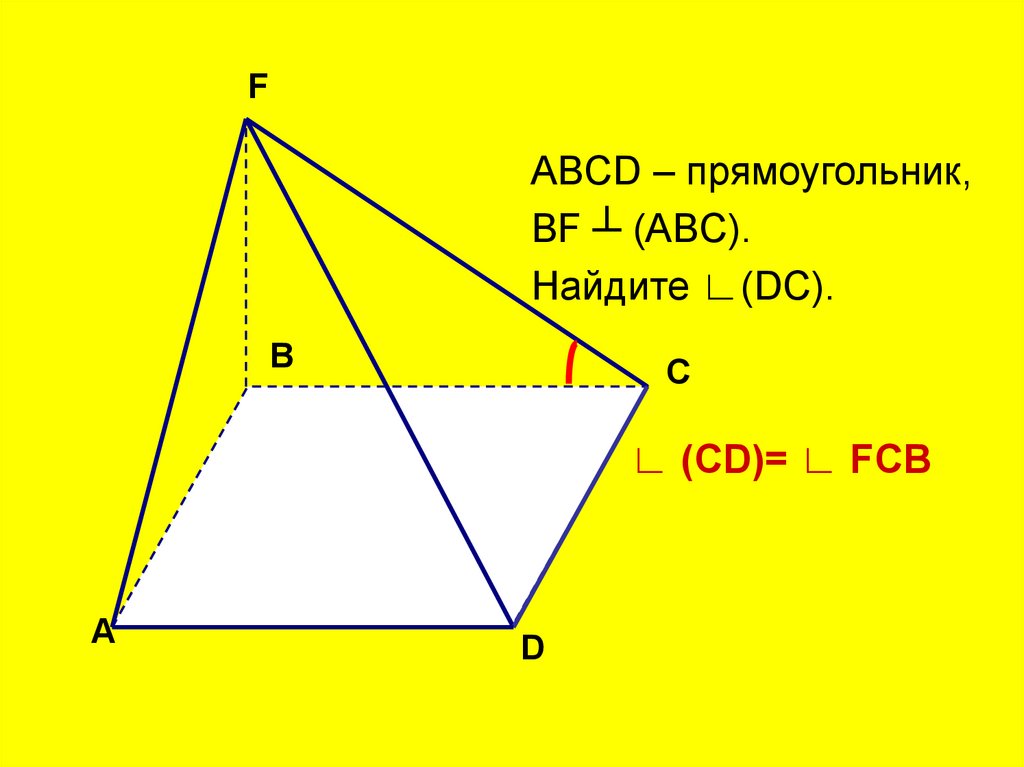
FABCD – прямоугольник,
BF ┴ (ABC).
Найдите ∟(DC).
B
C
∟ (СD)= ∟ FCB
А
D
7.
В1С1
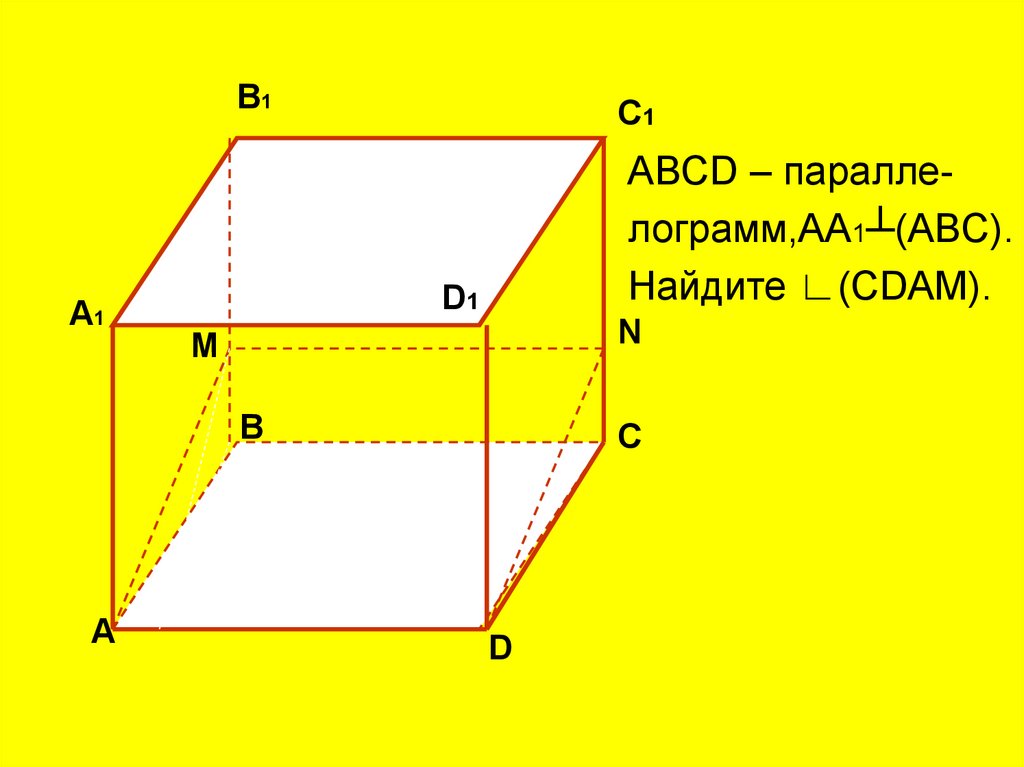
ABCD – параллелограмм,АА1┴(ABC).
Найдите ∟(СDАМ).
D1
А1
N
M
B
А
С
D
8.
В1С1
∟ CDAM= ∟ MKB
D1
А1
N
M
B
А
K
С
D
9.
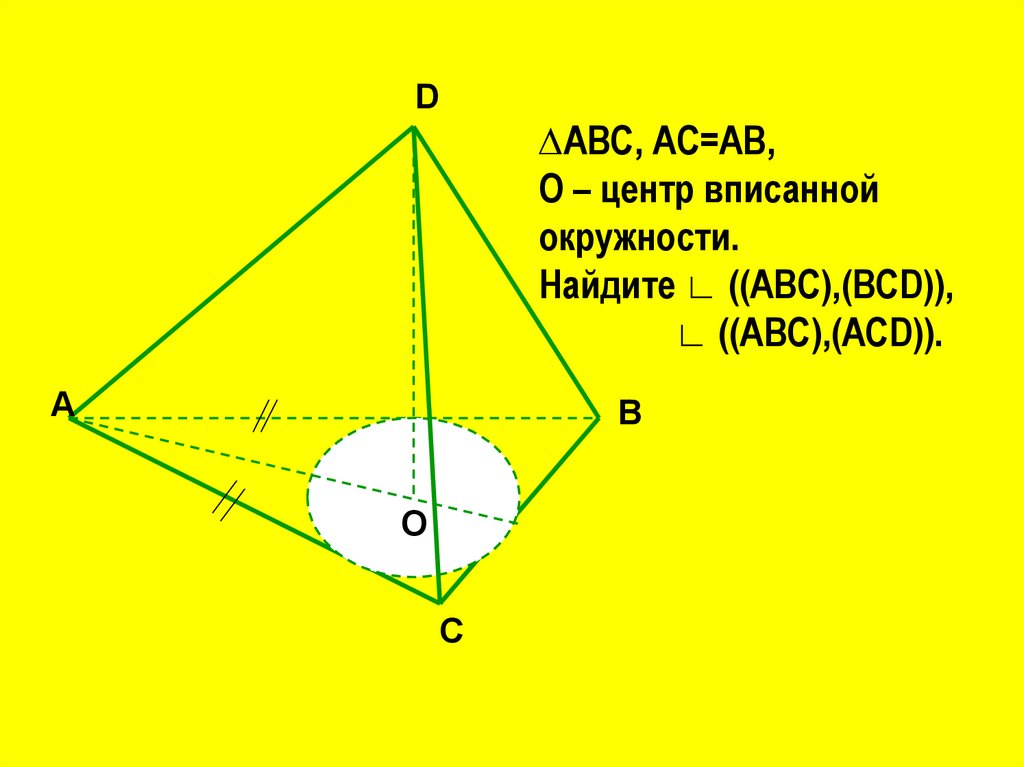
D∆АВС, АС=АВ,
О – центр вписанной
окружности.
Найдите ∟ ((АВС),(ВСD)),
∟ ((ABC),(ACD)).
А
В
О
С
10.
D∆АВС, АС=АВ,
О – центр вписанной
окружности.
Найдите ∟ ((АВС),(ВСD)),
∟ ((ABC),(ACD)).
А
В
О
P
L
С
∟((ABC),(BCD))= ∟ DPO
∟((ABC),(ACD))= ∟ DLO
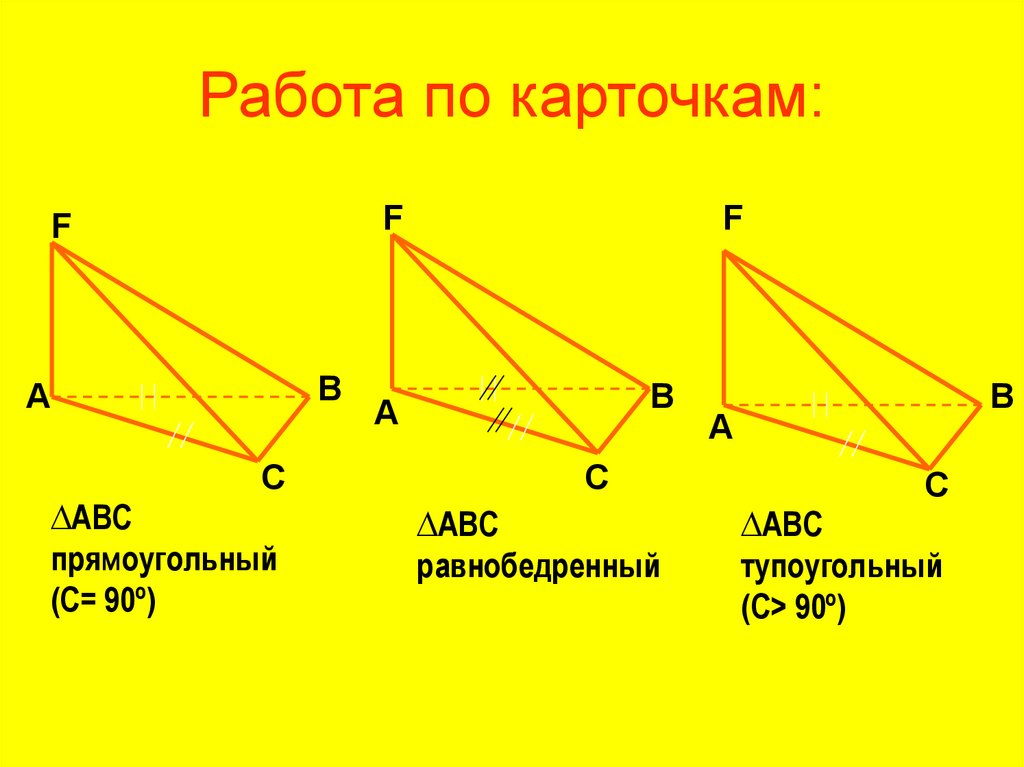
11. Работа по карточкам:
FF
В
А
С
∆АВС
прямоугольный
(С= 90º)
F
В
А
С
∆АВС
равнобедренный
В
А
С
∆АВС
тупоугольный
(С> 90º)
12.
FВ
А
С
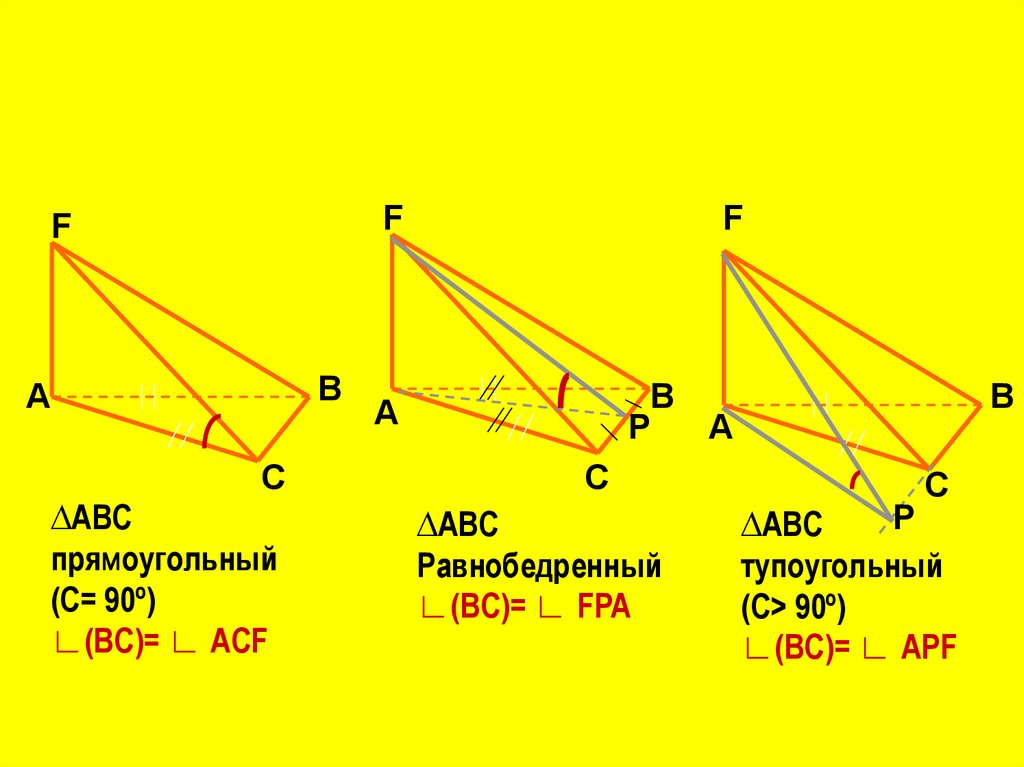
∆АВС
прямоугольный
(С= 90º)
∟(BC)= ∟ ACF
F
F
А
В
Р
А
С
∆АВС
Равнобедренный
∟(BC)= ∟ FPA
В
С
Р
∆АВС
тупоугольный
(С> 90º)
∟(BC)= ∟ APF
13.
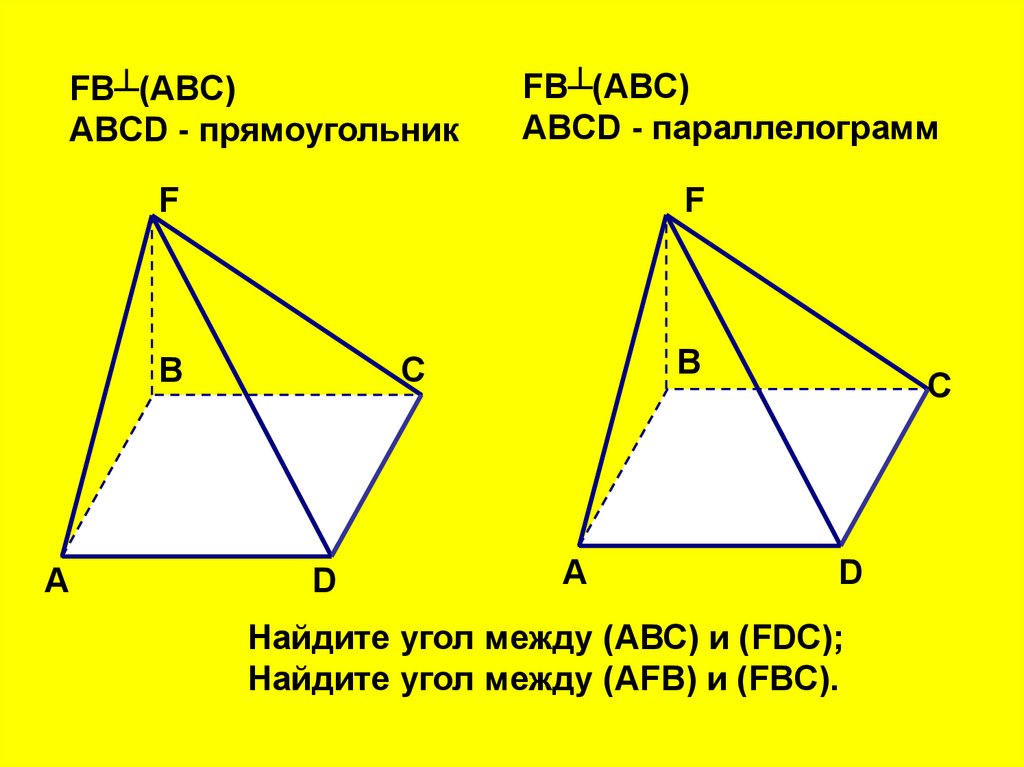
FB┴(ABC)ABCD - прямоугольник
FB┴(ABC)
ABCD - параллелограмм
F
F
В
А
B
С
D
A
C
D
Найдите угол между (АВС) и (FDC);
Найдите угол между (AFB) и (FBC).
14.
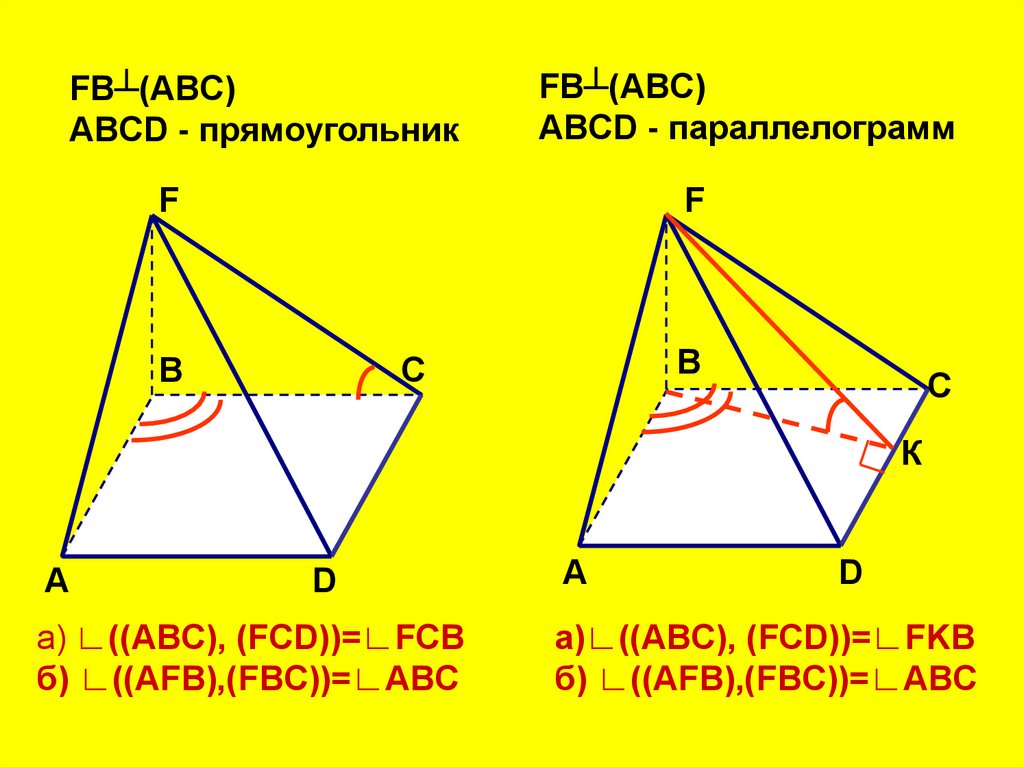
FB┴(ABC)ABCD - прямоугольник
FB┴(ABC)
ABCD - параллелограмм
F
F
В
B
С
C
К
А
D
a) ∟((ABC), (FCD))=∟FCB
б) ∟((AFB),(FBC))=∟ABC
A
D
а)∟((ABC), (FCD))=∟FKB
б) ∟((AFB),(FBC))=∟ABC
15. Шкала оценки:
• Если вы правильно выполнили задание1 - поставьте себе оценку «3».
• Если вы правильно выполнили задание
1,2(а) или 1, 2(б) - поставьте себе
оценку «4».
• Если вы правильно выполнили задание
1, 2 (а, б) - поставьте себе оценку «5».
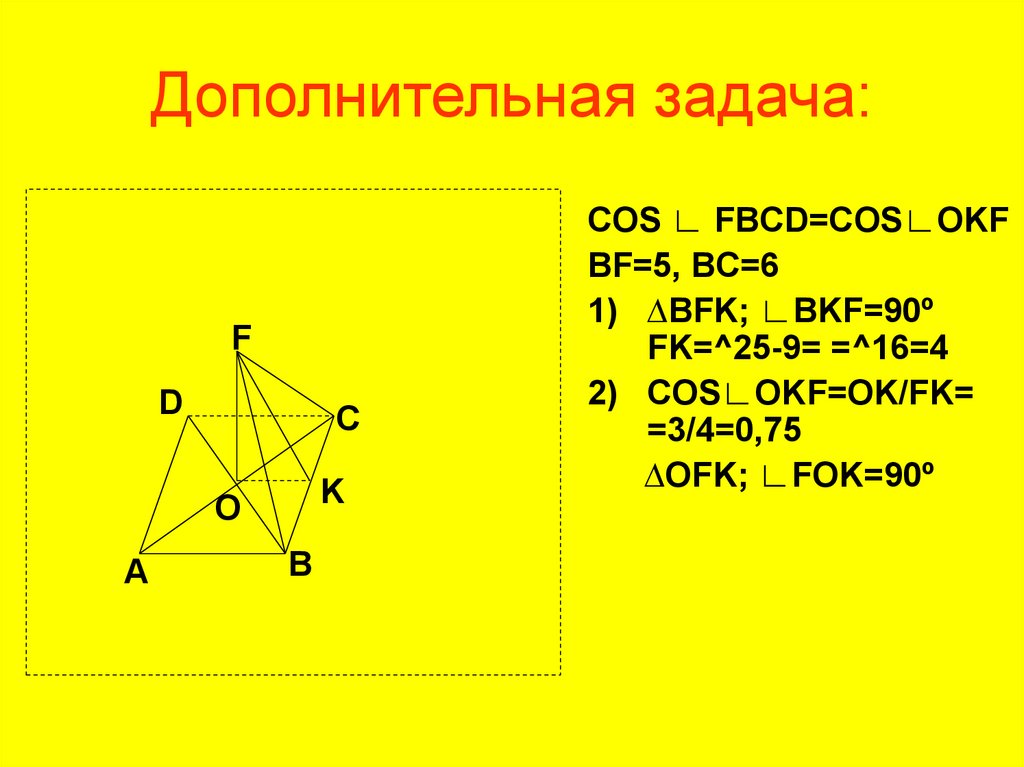
16. Дополнительная задача:
FD
C
K
O
A
B
COS ∟ FBCD=COS∟OKF
BF=5, BC=6
1) ∆BFK; ∟BKF=90º
FK=^25-9= =^16=4
2) COS∟OKF=OK/FK=
=3/4=0,75
∆OFK; ∟FOK=90º
17. Решить задачи:
• №172• №174
18. Изучение нового материала:
1. В тетраэдре FABCD – трехгранныеуглы
2. Показать на моделях
3. Теория и свойства через диск
19. Ограничение на значения плоских углов
• Каждый плоский угол многогранногоугла меньше 180º.
• Сумма всех плоских углов при вершине
многогранного угла меньше 360º.
• Во всяком многогранном угле любой
плоский угол меньше суммы всех
остальных.
20.
OD
К
A
H
М
С
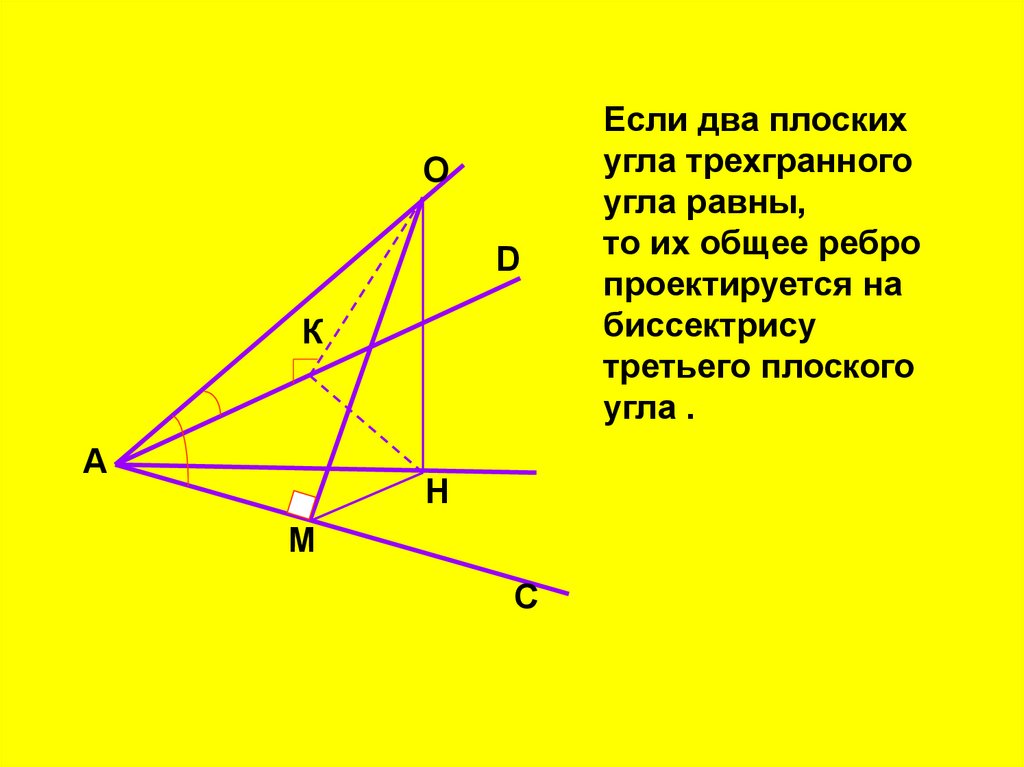
Если два плоских
угла трехгранного
угла равны,
то их общее ребро
проектируется на
биссектрису
третьего плоского
угла .
21. Решение задач:
Боковая поверхность треугольнойпирамиды равна S, а каждое из боковых
ребер l. Найдите плоские углы при
вершине, зная, что они образуют
арифметическую прогрессию П/3.
22. Проверка:
L,B,Y;B=L+П/3; Y=B+П/3=L+2П/3
Y<L+B L+2П/3<L+L+П/3;
L>П/3
Итак, L>П/3, но B=L+П/3>2П/3;
Y=L+2П/3>П/3+2П/3
Вывод: такого угла не существует.
23. Дополнительная задача:
Все грани параллелепипеда равные ромбы состороной a и острым углом 60º. Найдите
высоту параллелепипеда.
24. Домашнее задание:
1. п. 22,23.2. Изучить определение
перпендикулярных плоскостей,
теорему














 Математика
Математика








