Похожие презентации:
Вписанные и описанные окружности
1.
Вписанные иописанные окружности
2.
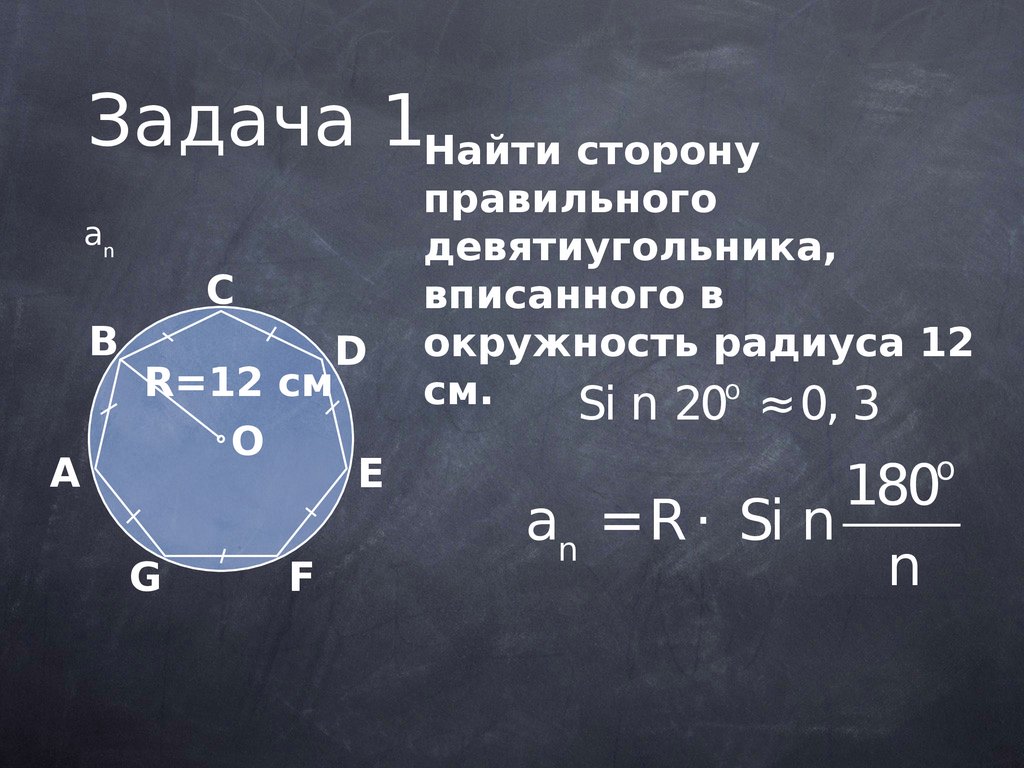
Задача 1Найти сторонуan
C
B
A
R=12 см
O
G
F
D
E
правильного
девятиугольника,
вписанного в
окружность радиуса 12
o
см.
Si n 20 ≈0, 3
o
180
an =R ⋅ Si n
n
3.
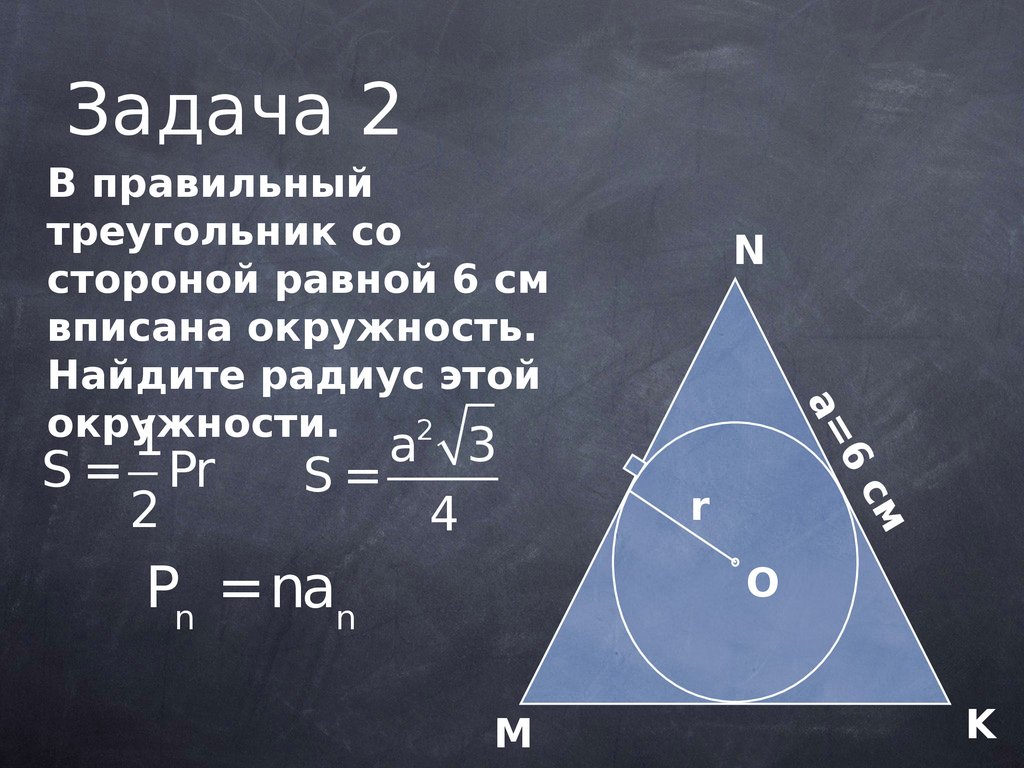
Задача 2В правильный
треугольник со
стороной равной 6 см
вписана окружность.
Найдите радиус этой
окружности.
2
1
3
r
4
Pn =nan
см
S=
6
a=
S = Pr
2
a
N
O
M
K
4.
2 o1
AB
=a
=R
⋅
Si
n60
M
N
3
M
N
=2r
3
P(
ABC)
=3
3
R
P(
M
NK)
=6
3
⋅
r
AB
=R
3
3
S = Pr
S=
2
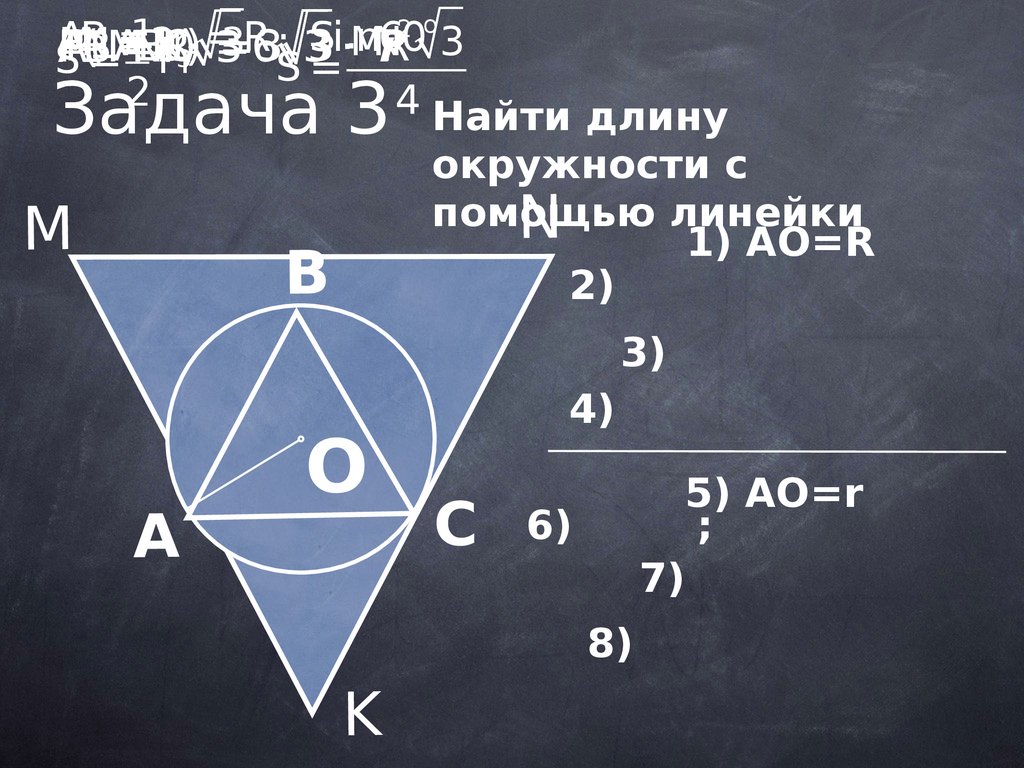
4 Найти длину
окружности с
помощью
линейки
N
M
1) AO=R
B
2)
Задача 3
3)
A
O
4)
C
5) AO=r
;
7)
6)
8)
K
5.
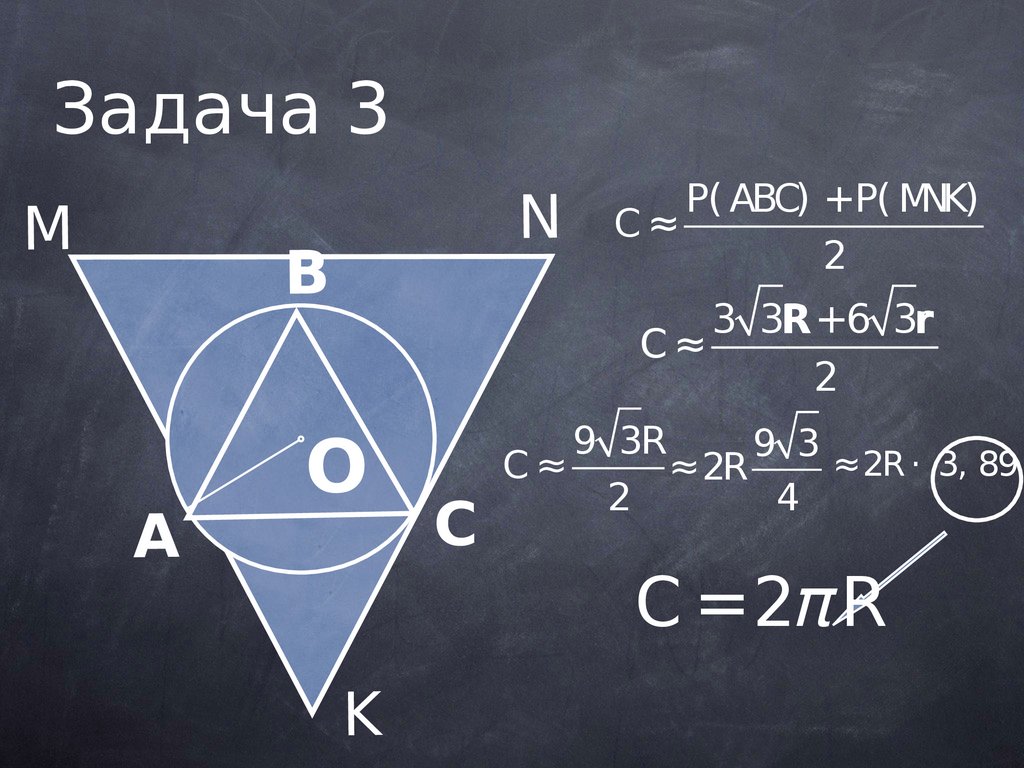
Задача 3M
N
B
A
P( ABC) +P( MNK)
C≈
2
3 3R
R +6 3rr
C≈
2
O
C
9 3R
9 3
≈2R ⋅ 3, 89
C≈
≈2R
2
4
C =2π R
K
6.
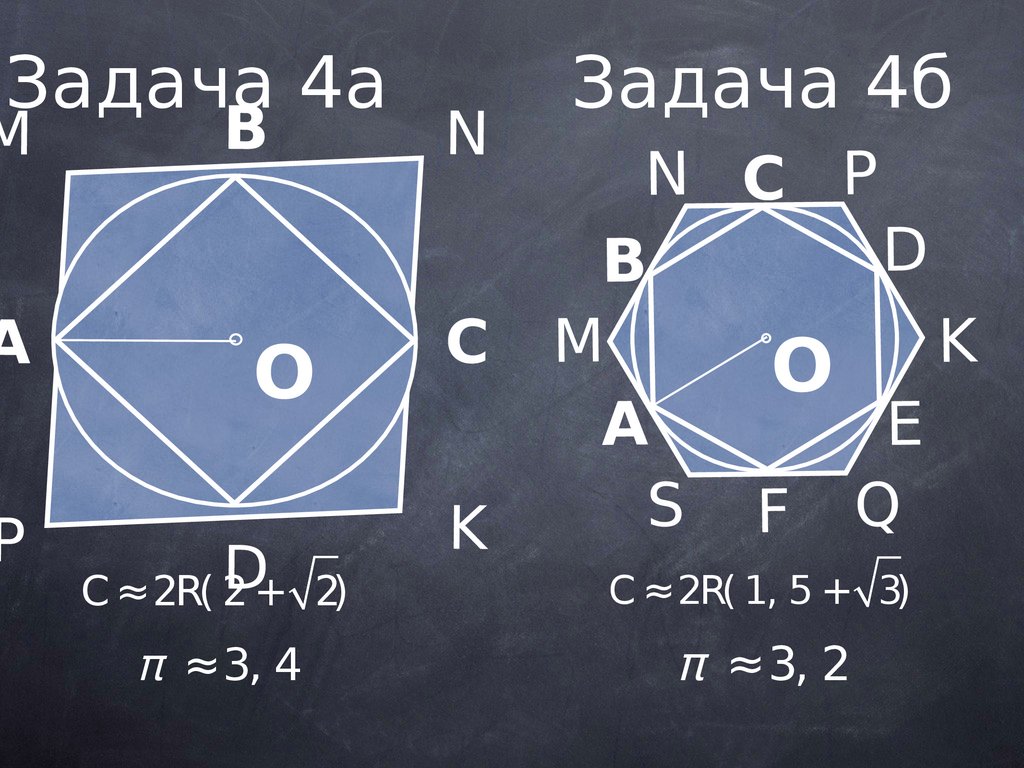
Задача 4аM
A
P
B
O
D
C ≈2R( 2 +
π ≈3, 4
N
C
K
2)
Задача 4б
N C P
D
B
K
M
O
E
A
S F Q
C ≈2R( 1, 5 + 3)
π ≈3, 2
7.
n-угольникВ 200-х годах до
н.э. Архимед
просчитал число
«пи» для
π96-тиугольника
≈3, 142857142857143
В 416-х годах н.э.
Цзу Чунжи
просчитал число
«пи» для
12288-тиугольника
3, 1415926 <π <3, 1415927
O
8.
19октября
2011
года
Александр
Йи
и
Сигэру
Кондо
рассчитали
число
«пи»
с
точностью
в
10
триллионов
знаков
после
запятой
9.
То, что принято бездоказательств, может
быть и отвергнуто без
доказательств.
(Евклид)




 Математика
Математика








