Тест по теме: "Векторы в пространстве"

1. МКОУ «Погорельская СОШ» Кощеев М.М.

Тест по теме:
«Векторы в
пространстве»
Вариант 1
Вариант 2
Использован шаблон создания тестов в PowerPoint

2. Результат теста

Верно: 10
Ошибки: 0
Отметка: 5
Время: 0 мин. 26 сек.
ещё

3. Вариант 1

а) Векторы называются компланарными, если при откладывании их от одной и
той же точки они будут лежать в одной плоскости
в) Для сложения трех некомпланарных векторов используют правило
параллелепипеда
г) Любые три вектора компланарны
д) Любые три вектора некомпланарны
3

4. Вариант 1

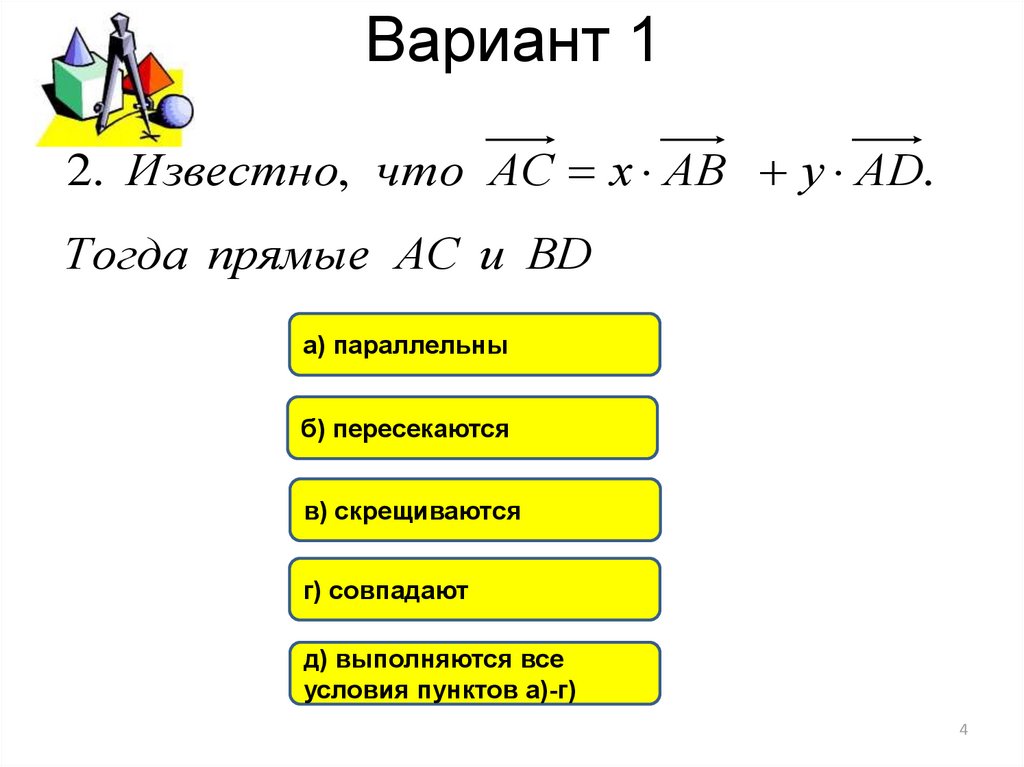
2. Известно, что АС х АВ у АD.
Тогда прямые АС и ВD
а) параллельны
б) пересекаются
в) скрещиваются
г) совпадают
д) выполняются все
условия пунктов а)-г)
4

5. Вариант 1

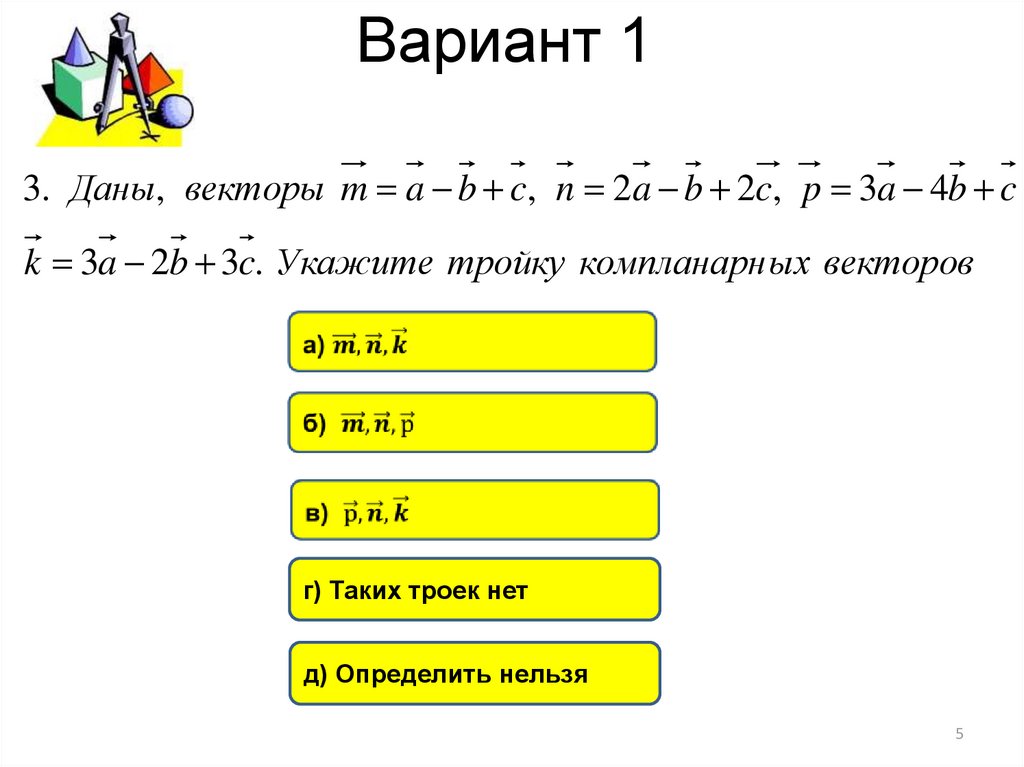
3. Даны, векторы m a b c, n 2a b 2c, p 3a 4b c
k 3a 2b 3c. Укажите тройку компланарн ых векторов
г) Таких троек нет
д) Определить нельзя
5

6. Вариант 1

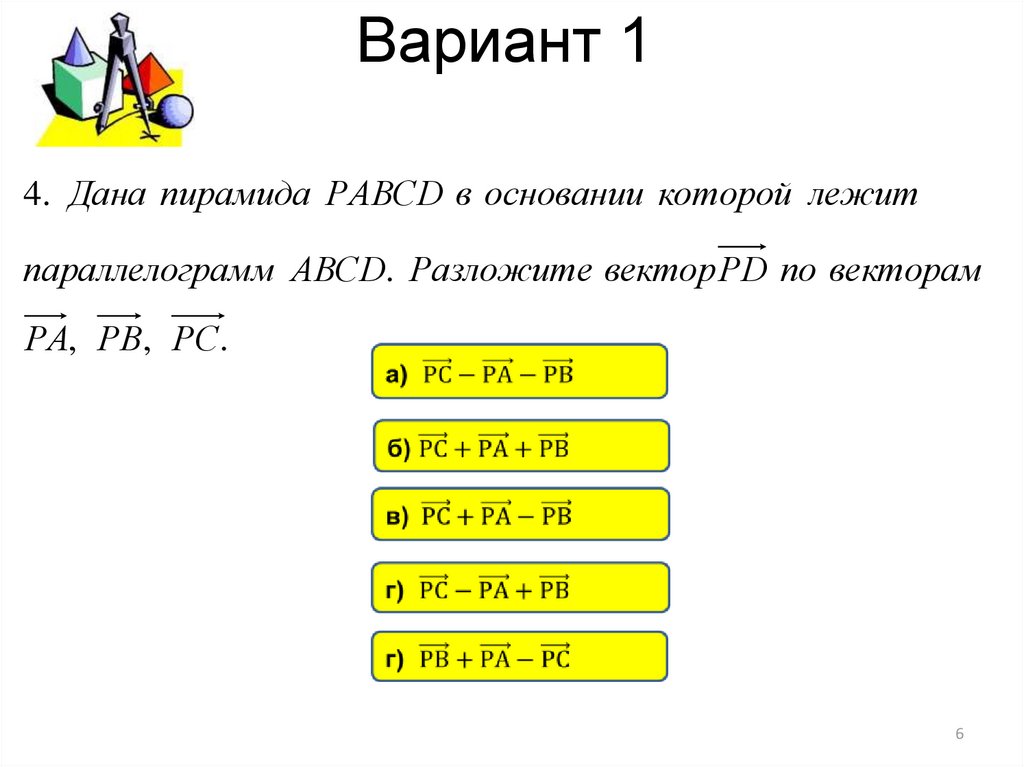
4. Дана пирамида РАВСD в основании которой лежит
параллелограмм АВСD. Разложите вектор РD по векторам
РА, РВ, РС.
6

7. Вариант 1

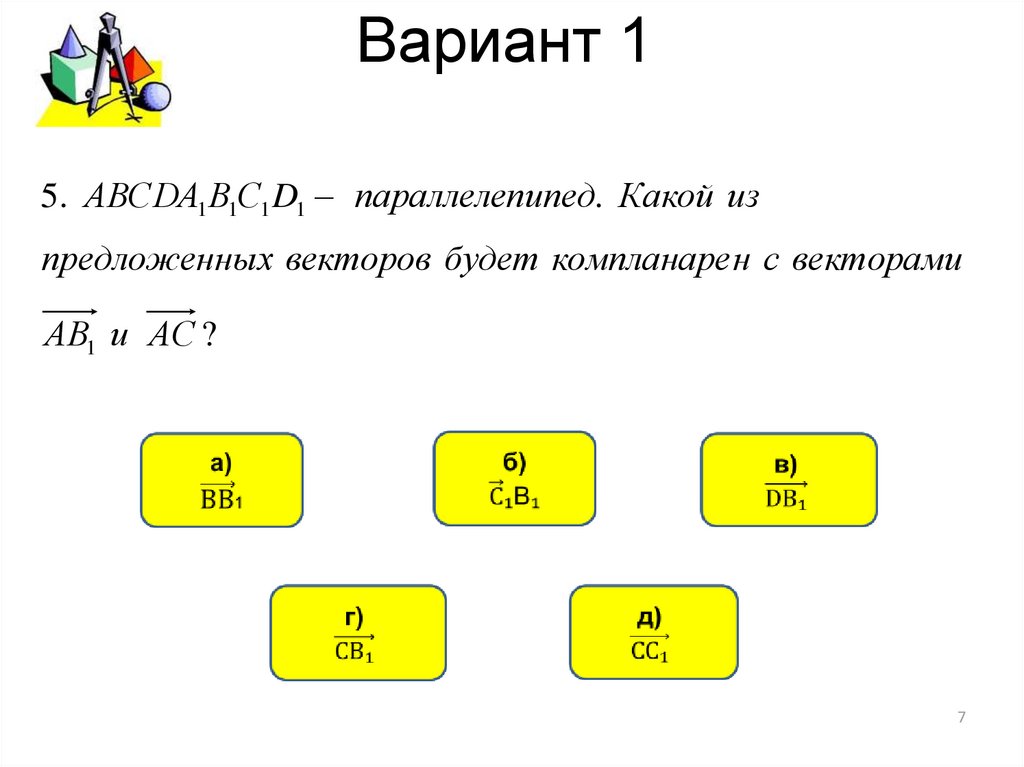
5. АВСDА1 В1С1 D1 параллелепипед. Какой из
предложенных векторов будет компланаре н с векторами
АВ1 и АС ?
7

8. Вариант 1

6. Векторы а, р, b некомплана рны :
а) Если при откладывании из одной точки они не лежат в одной плоскости
б) Два из данных векторов коллинеарны
в) Один из данных векторов нулевой
8

9. Вариант 1

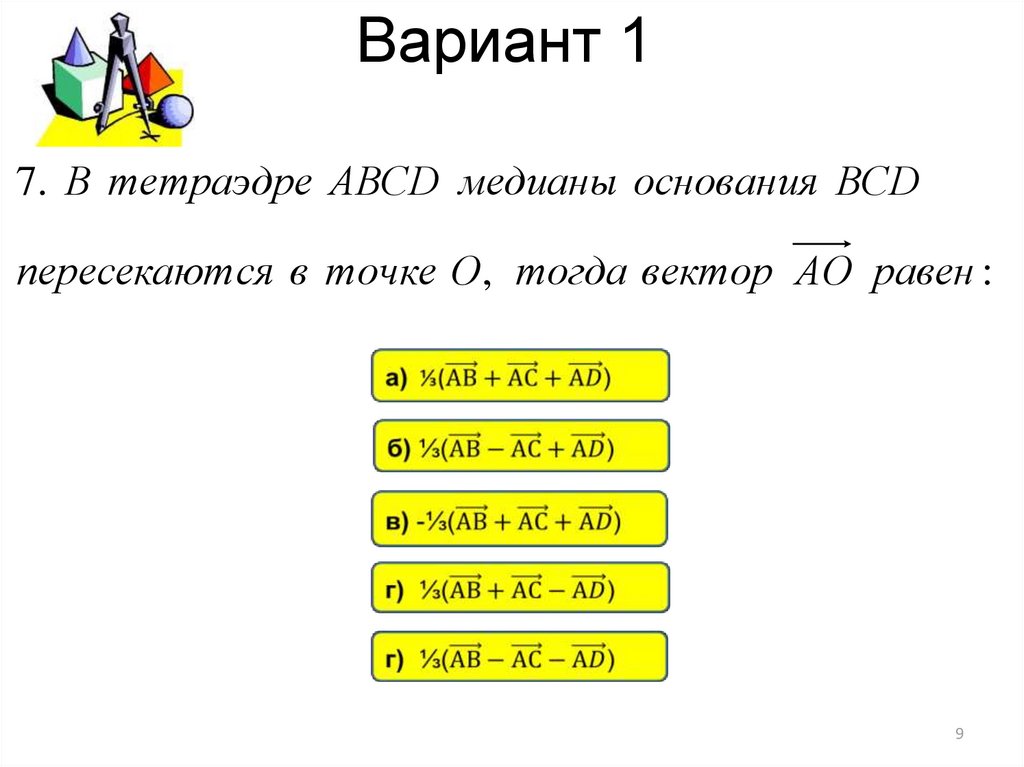
7. В тетраэдре АВСD медианы основания ВСD
пересекают ся в точке О, тогда вектор АО равен :
9

10. Вариант 1

8. Даны векторы с 2а 3b, d 3a 2b, p 2c 3d .
Найдите коэффициен ты х и у разложения вектора р,
по векторам а и b.
а)
х=13, у=0
б)
х=-5, у=-12
в)
х=5, у=-12
г)
х=-5, у=0
д)
х=5, у=12
10

11. Вариант 1

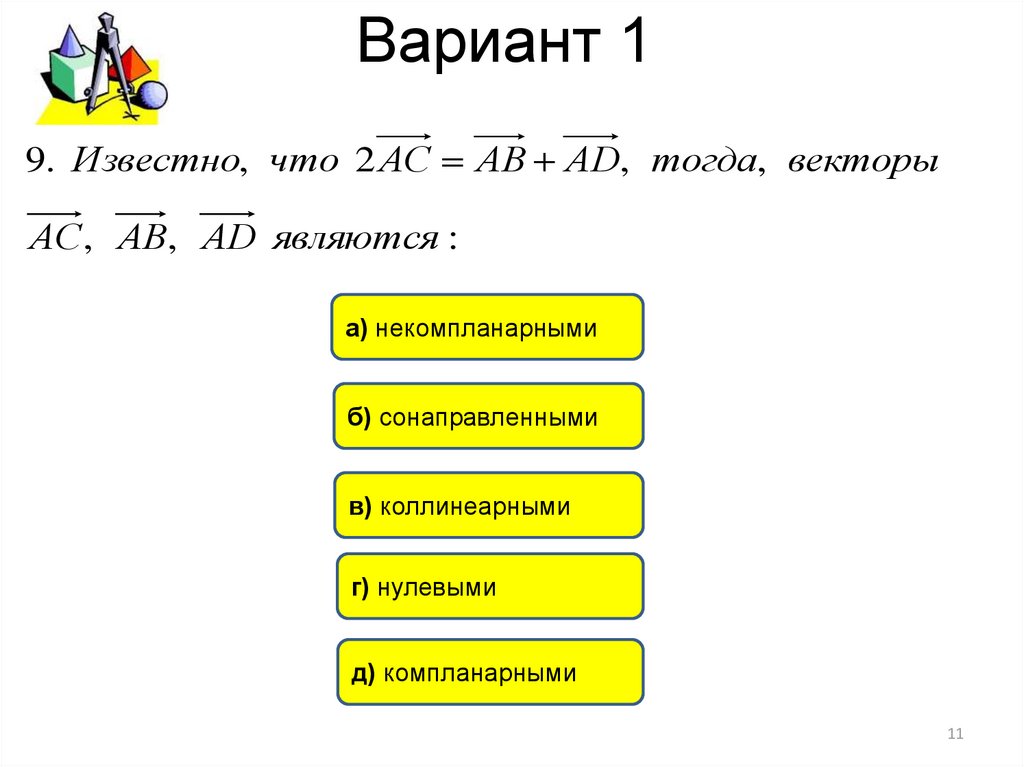
9. Известно, что 2 АС АВ АD, тогда, векторы
АС, АВ, АD являются :
а) некомпланарными
б) сонаправленными
в) коллинеарными
г) нулевыми
д) компланарными
11

12. Вариант 1

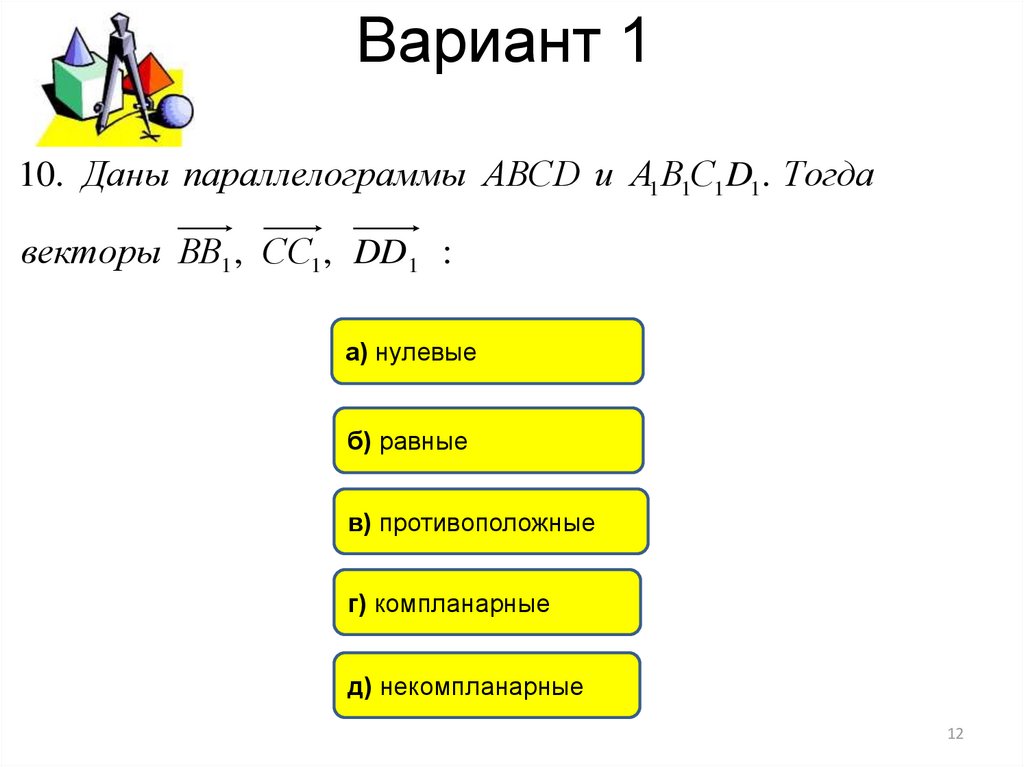
10. Даны параллелограммы АВСD и А1 В1С1 D1. Тогда
векторы ВВ1 , СС1 , DD 1 :
а) нулевые
б) равные
в) противоположные
г) компланарные
д) некомпланарные
12

13. Вариант 2

а) Три вектора будут компланарными, если один из них нулевой
в) Для сложения трех некомпланарных векторов не используют правило
параллелепипеда
г) Любые два вектора некомпланарны
д) Три нулевых вектора компланарны
13

14. Вариант 2

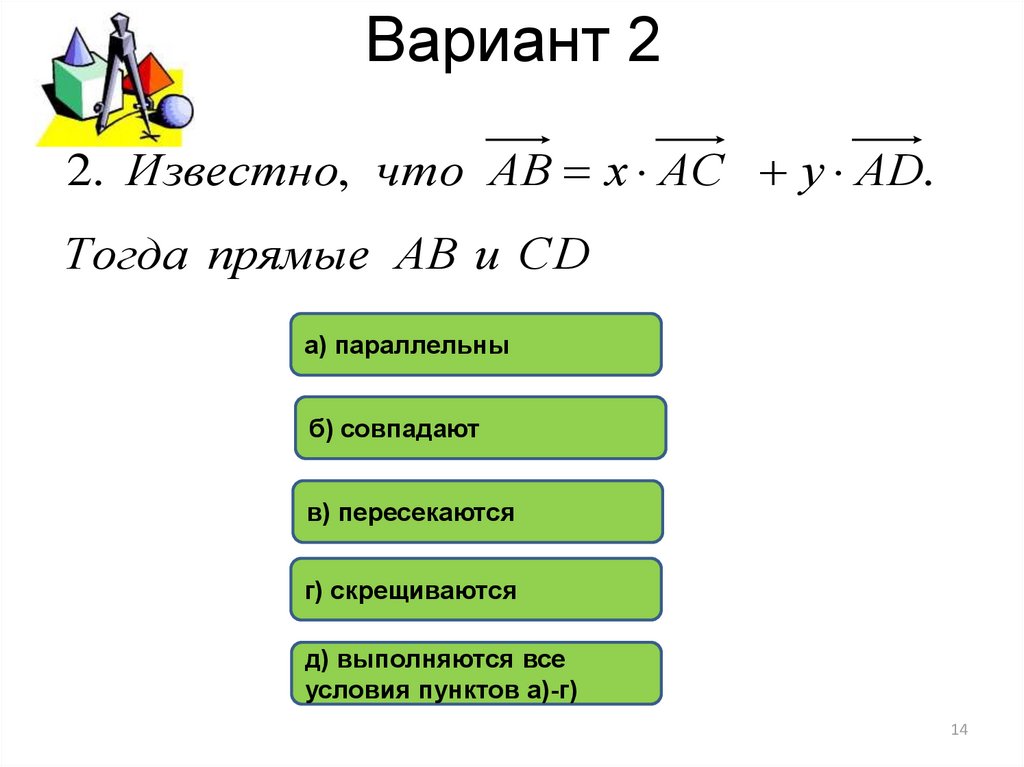
2. Известно, что АВ х АС у АD.
Тогда прямые АВ и СD
а) параллельны
б) совпадают
в) пересекаются
г) скрещиваются
д) выполняются все
условия пунктов а)-г)
14

15. Вариант 2

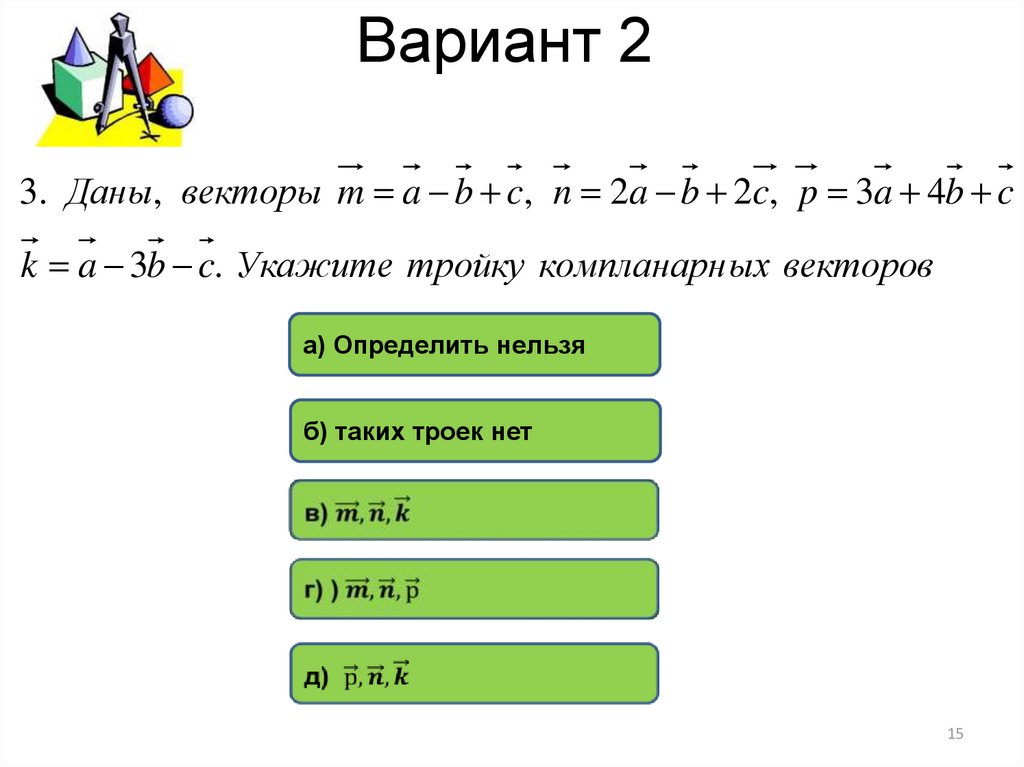
3. Даны, векторы m a b c, n 2a b 2c, p 3a 4b c
k a 3b c. Укажите тройку компланарн ых векторов
а) Определить нельзя
б) таких троек нет
15

16. Вариант 2

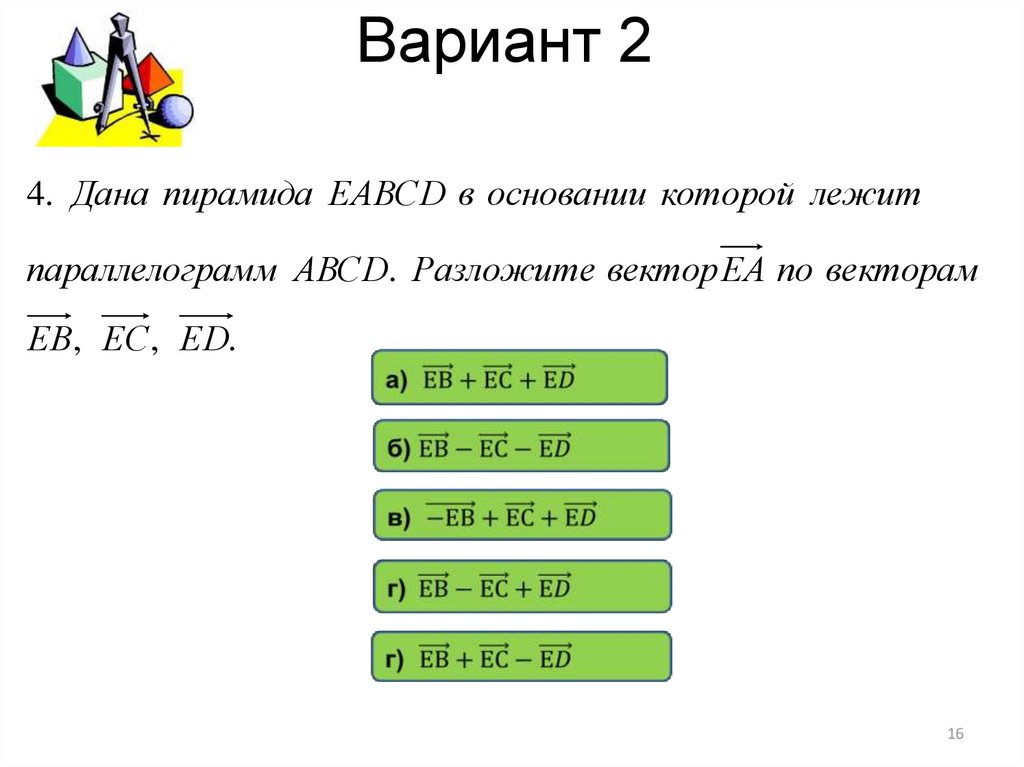
4. Дана пирамида ЕАВСD в основании которой лежит
параллелограмм АВСD. Разложите вектор ЕА по векторам
ЕВ, ЕС, ЕD.
16

17. Вариант 2

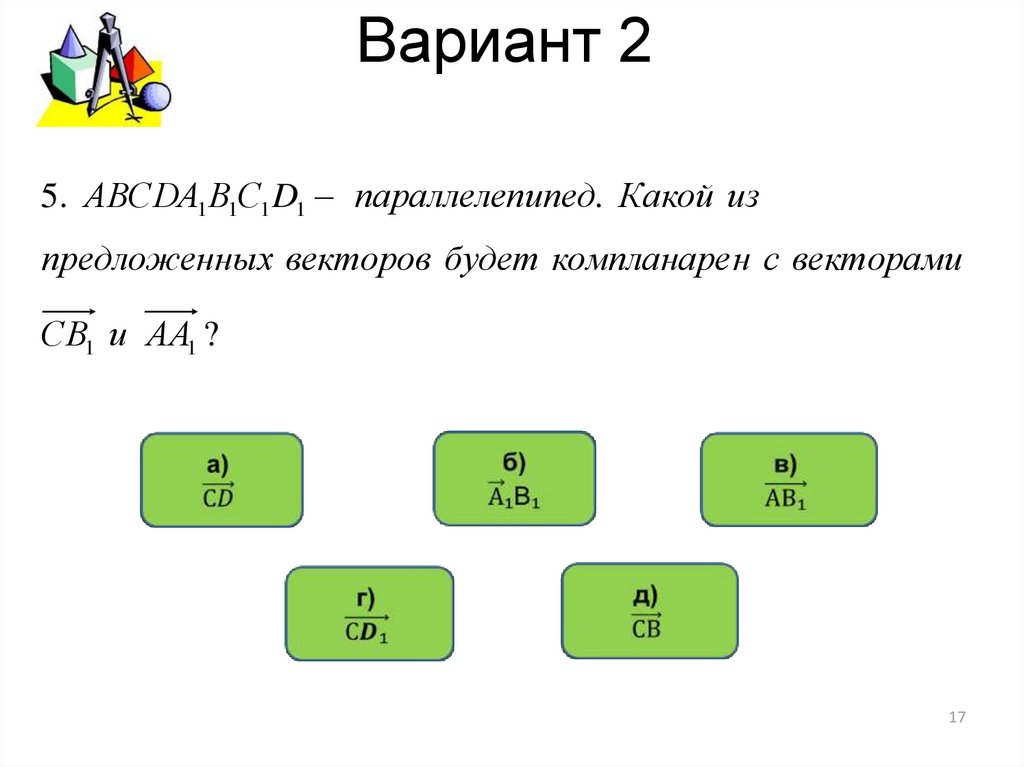
5. АВСDА1 В1С1 D1 параллелепипед. Какой из
предложенных векторов будет компланаре н с векторами
СВ1 и АА1 ?
17

18. Вариант 2

6. Векторы а, р, b компланарн ы :
а) Если при откладывании из одной точки они не лежат в одной плоскости
б) Два из данных векторов равны
в) Если любой вектор можно разложить по данным векторам
г) Если их сумму можно найти с помощью правила параллелепипеда
д) Если их длины являются измерениями параллелепипеда.
18

19. Вариант 2

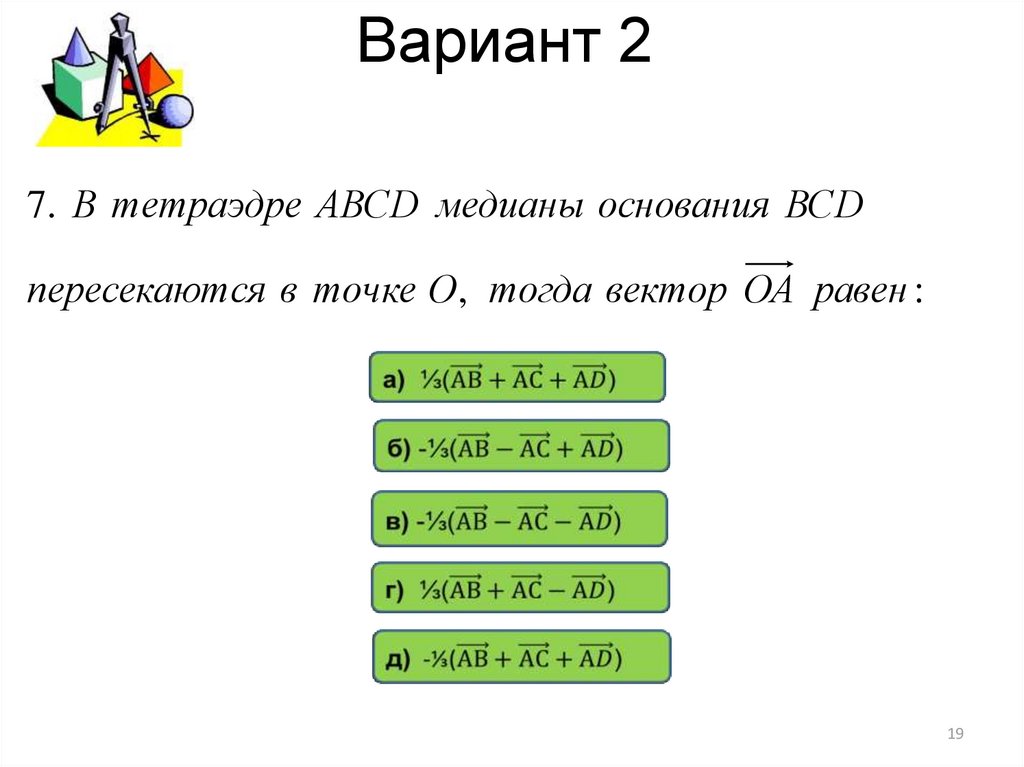
7. В тетраэдре АВСD медианы основания ВСD
пересекают ся в точке О, тогда вектор ОА равен :
19

20. Вариант 2

8. Даны векторы с 2а 3b, d 3a 2b, p 2c 3d .
Найдите коэффициен ты х и у разложения вектора р,
по векторам а и b.
а)
х=13, у=0
б)
х=-5, у=-12
в)
х=5, у=-12
г)
х=-5, у=0
д)
х=5, у=12
20

21. Вариант 2

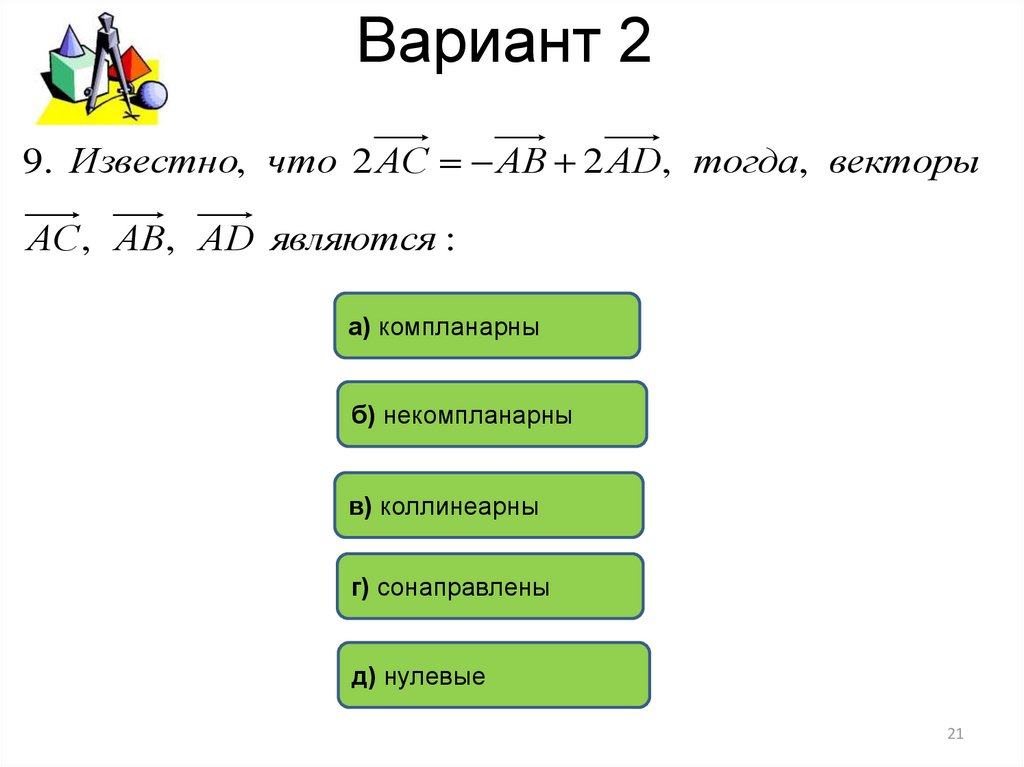
9. Известно, что 2 АС АВ 2 АD, тогда, векторы
АС, АВ, АD являются :
а) компланарны
б) некомпланарны
в) коллинеарны
г) сонаправлены
д) нулевые
21

22. Вариант 2

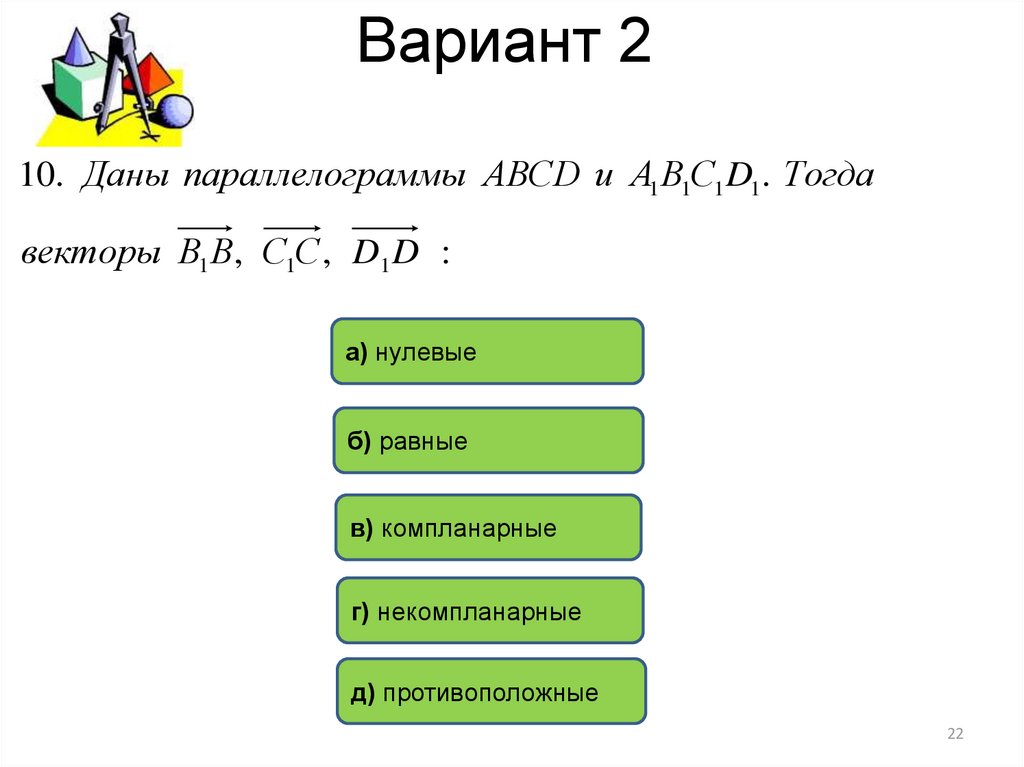
10. Даны параллелограммы АВСD и А1 В1С1 D1. Тогда
векторы В1 В, С1С , D1 D :
а) нулевые
б) равные
в) компланарные
г) некомпланарные
д) противоположные
22

23.

Ключи к тесту: Правильные многогранники.
1вариант
1
2
3
4
5
6
7
8
9
10
Отв.
д
б
а
в
г
а
а
б
д
г
2вариант
1
2
3
4
5
6
7
8
9
10
Отв.
г
в
д
г
д
б
д
в
а
в
Литература
Ю.А. Киселева. Геометрия 9-11 классы. Обобщающее повторение. Изд-во «Учитель», 2009г.
23