Похожие презентации:
Переключательные и комбинационнные схемы. ДМ.14
1. Дискретная математика
2. Схемы переключателей
Релейно-контактные схемы(или переключательные
схемы) широко используются в
технике автоматического
управления.
3. Схемы переключателей
Под переключательной схемойпонимают схематическое
изображение некоторого
устройства, состоящее из
следующих элементов:
1) переключателей (ключей);
2) соединяющих их проводников;
3) входов в схему и выходов из
нее (полюсов).
4. Схемы переключателей
Простейшая схема содержит одинпереключатель Р и имеет один
вход и один выход.
Переключателю Р ставится в
соответствие истинное
высказывание Р, гласящее
«переключатель Р замкнут», что
соответствует ситуации: «ток
идет»
5. Схемы переключателей
Простейшая схема содержит одинпереключатель Р и имеет один
вход и один выход.
Переключателю Р ставится в
соответствие истинное
высказывание Р, гласящее
«переключатель Р замкнут».
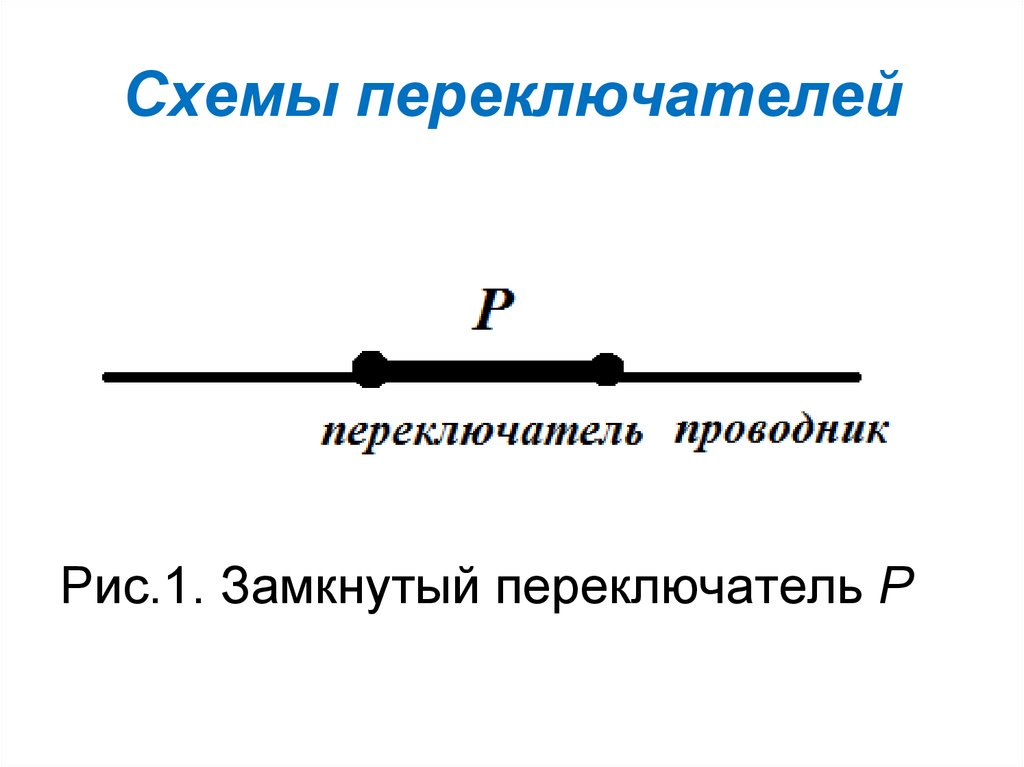
Замкнутый переключатель Р
приведен на рис.1
6. Схемы переключателей
Рис.1. Замкнутый переключатель Р7. Схемы переключателей
Переключателю Р ставится всоответствие истинное
высказывание: «переключатель Р
разомкнут» или «переключатель
Р замкнут».
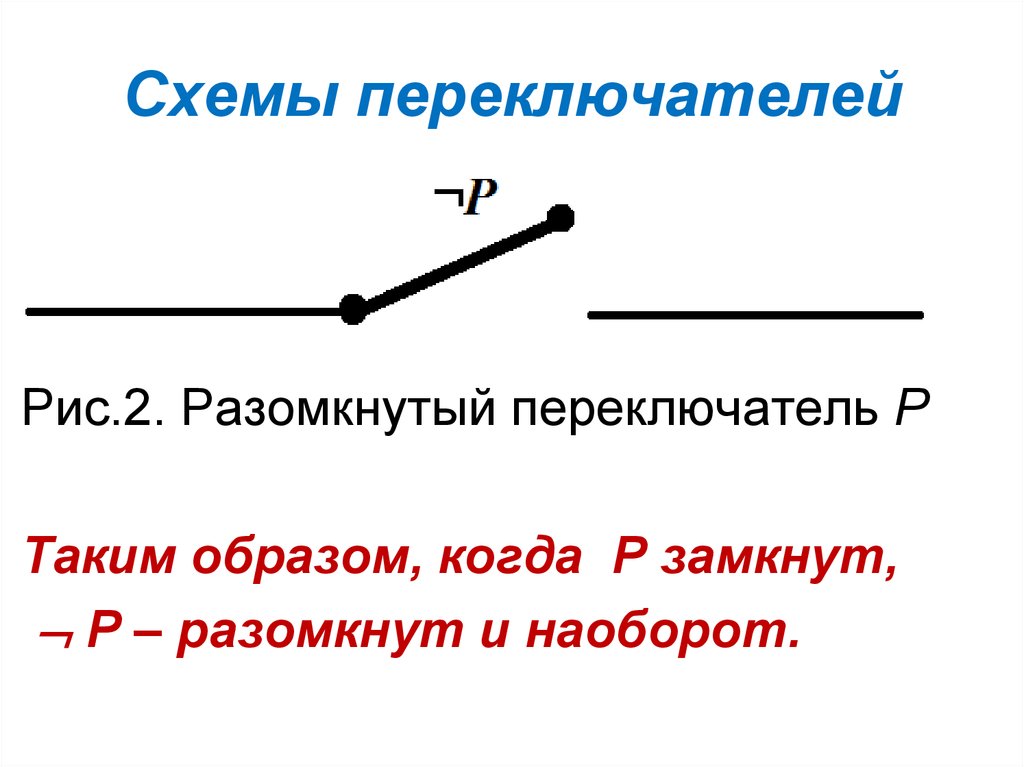
Разомкнутый переключатель Р
приведен на рис. 2
8. Схемы переключателей
Рис.2. Разомкнутый переключатель РТаким образом, когда Р замкнут,
Р – разомкнут и наоборот.
9. Схемы переключателей
Если высказывание Р истинно, топереключатель Р замкнут – схема
пропускает ток,
если высказывание Р ложно, то
переключатель Р разомкнут –
схема не пропускает ток.
Следовательно, любому высказыванию
может быть поставлена в соответствие
переключательная схема с двумя
полюсами (двухполюсная схема).
10. Схемы переключателей
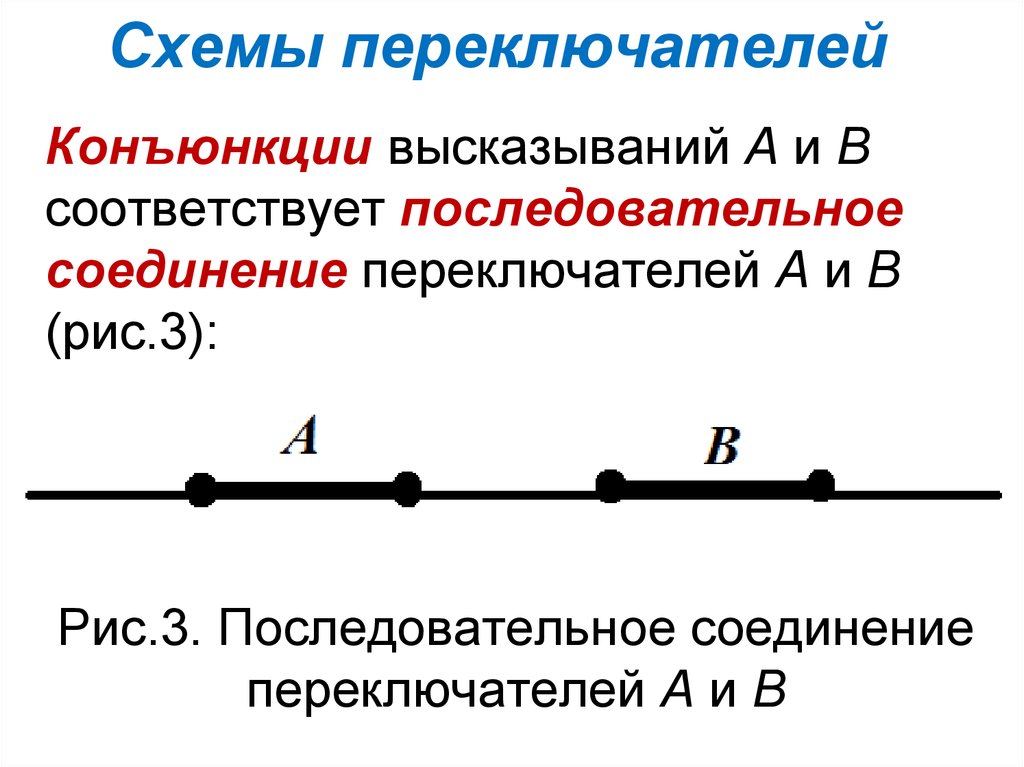
Конъюнкции высказываний А и Всоответствует последовательное
соединение переключателей А и В
(рис.3):
Рис.3. Последовательное соединение
переключателей А и В
11. Схемы переключателей
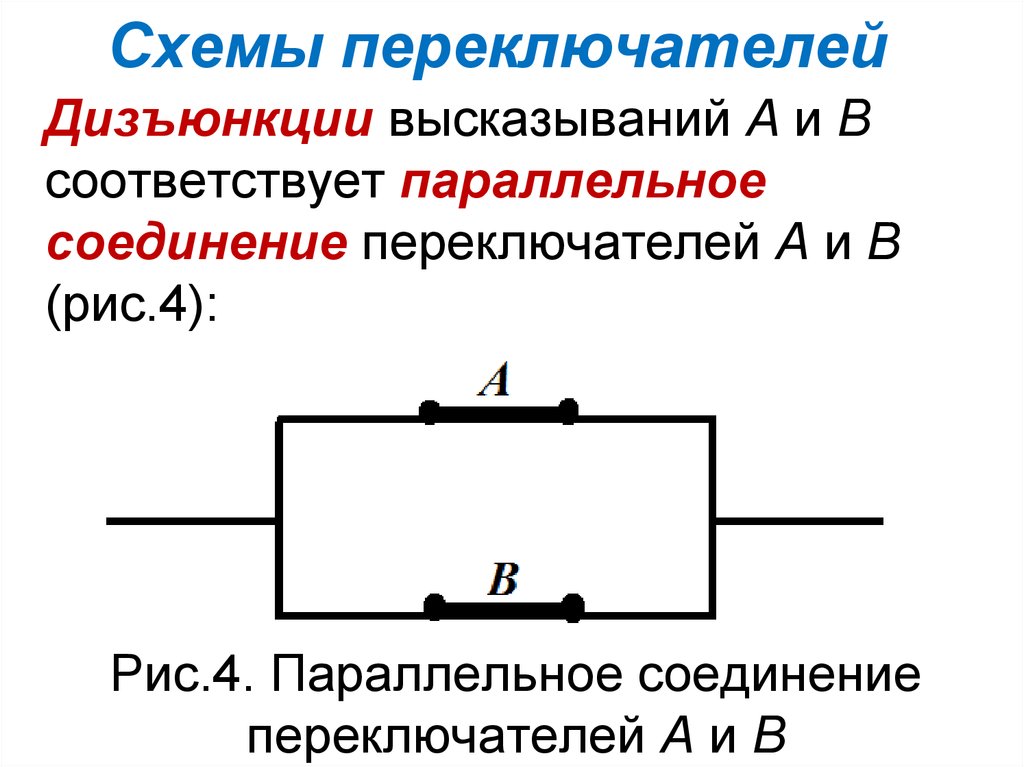
Дизъюнкции высказываний А и Всоответствует параллельное
соединение переключателей А и В
(рис.4):
Рис.4. Параллельное соединение
переключателей А и В
12. Схемы переключателей
На рисунке 5 приведена схема,содержащая переключатели
А и А, В и В, С и С.
Рис.5. Схема переключателей параллельно-последовательными соединениями.
13. Схемы переключателей
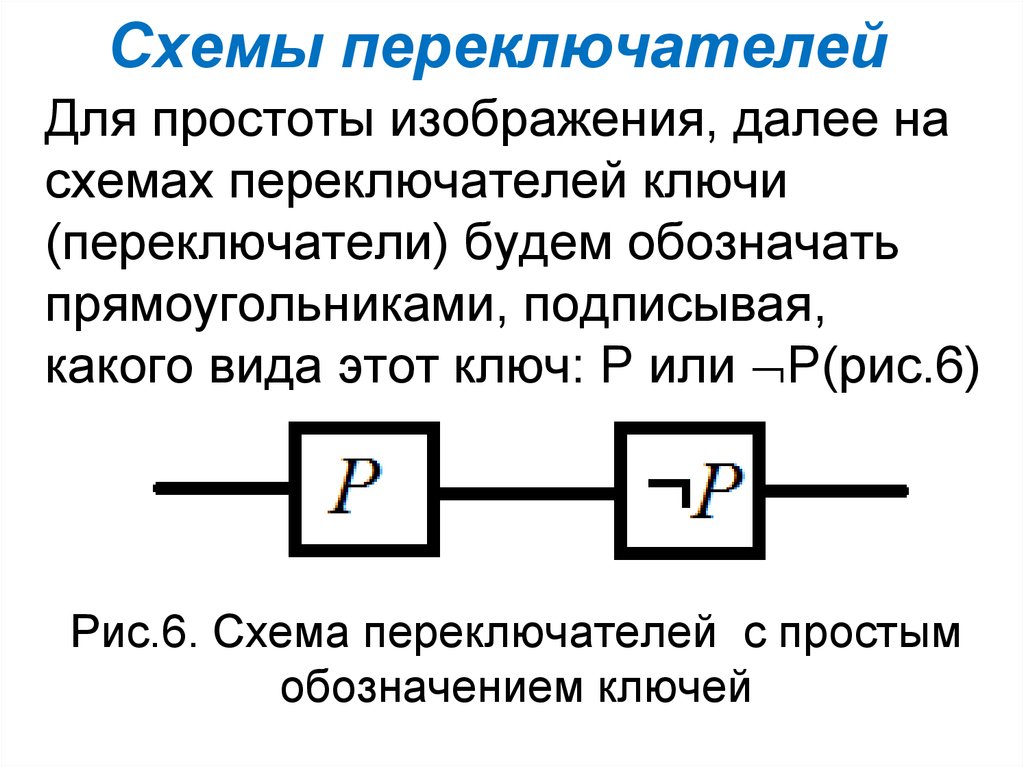
Для простоты изображения, далее насхемах переключателей ключи
(переключатели) будем обозначать
прямоугольниками, подписывая,
какого вида этот ключ: Р или Р(рис.6)
Рис.6. Схема переключателей с простым
обозначением ключей
14. Схемы переключателей
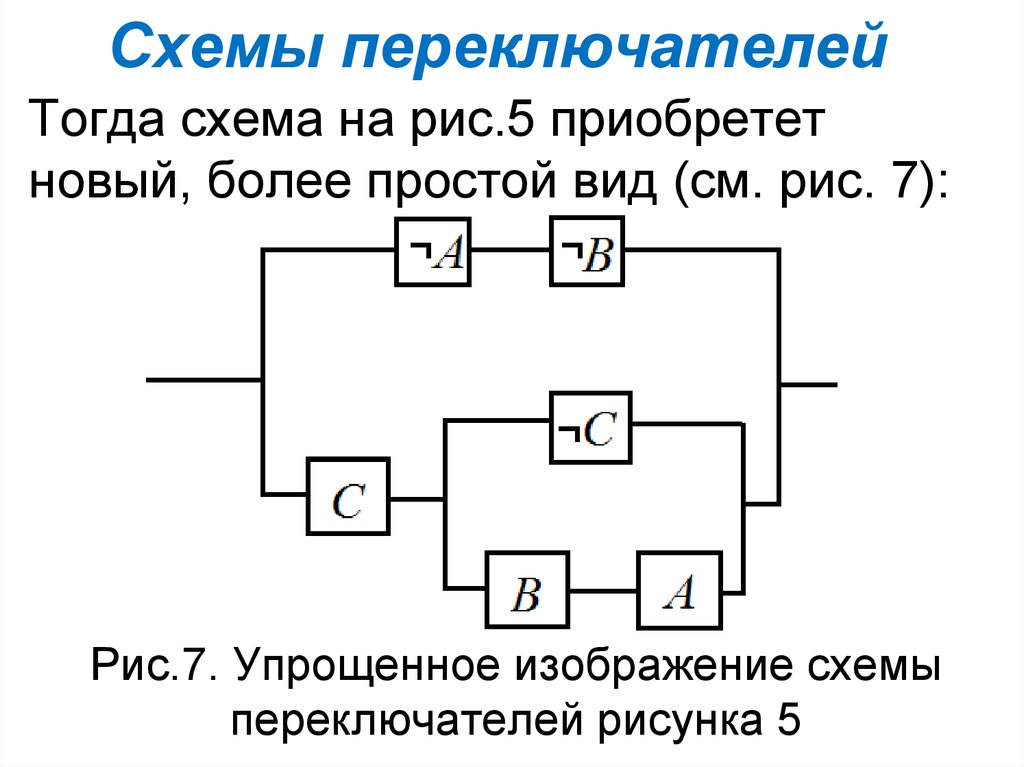
Тогда схема на рис.5 приобрететновый, более простой вид (см. рис. 7):
Рис.7. Упрощенное изображение схемы
переключателей рисунка 5
15. Схемы переключателей
Так как любая формула логикивысказываний может быть
записана в виде ДНФ или КНФ, то
ясно, что любой формуле можно
сопоставить схему
переключателей. Причем,
упрощение формулы ведет к
упрощению схемы.
16. Схемы переключателей
Упростим схему переключателей,приведенную на рисунке 7.
Построим булеву формулу,
соответствующую данной схеме.
17. Схемы переключателей
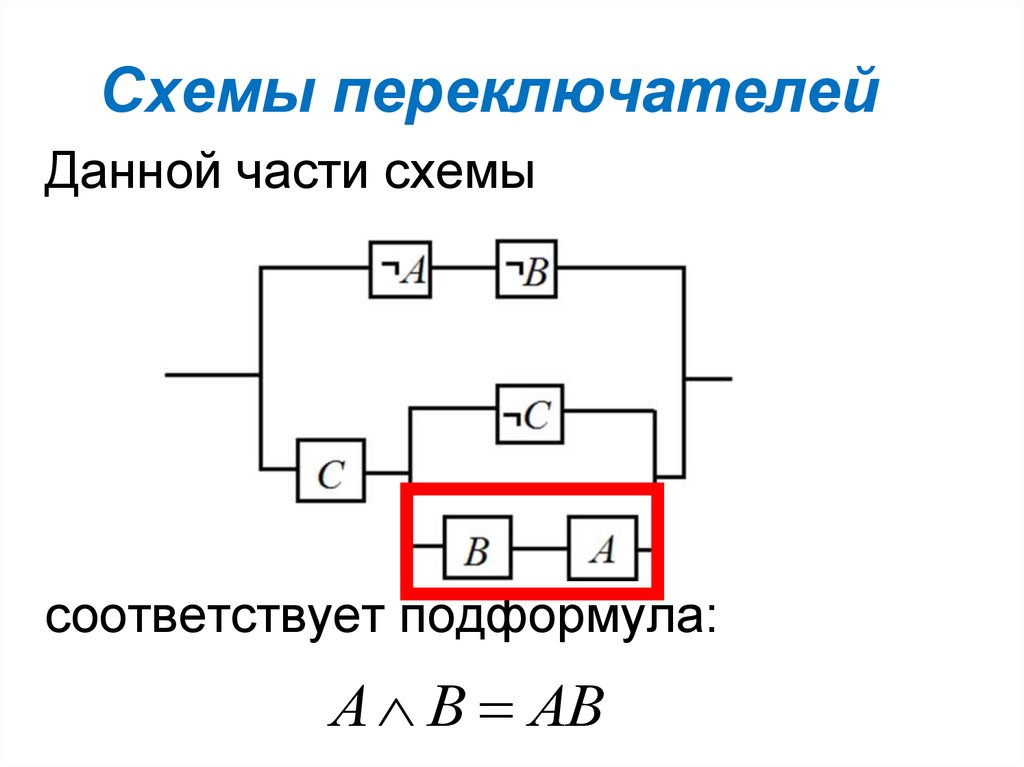
Данной части схемысоответствует подформула:
А В АВ
18. Схемы переключателей
Данной части схемысоответствует подформула:
А В АВ
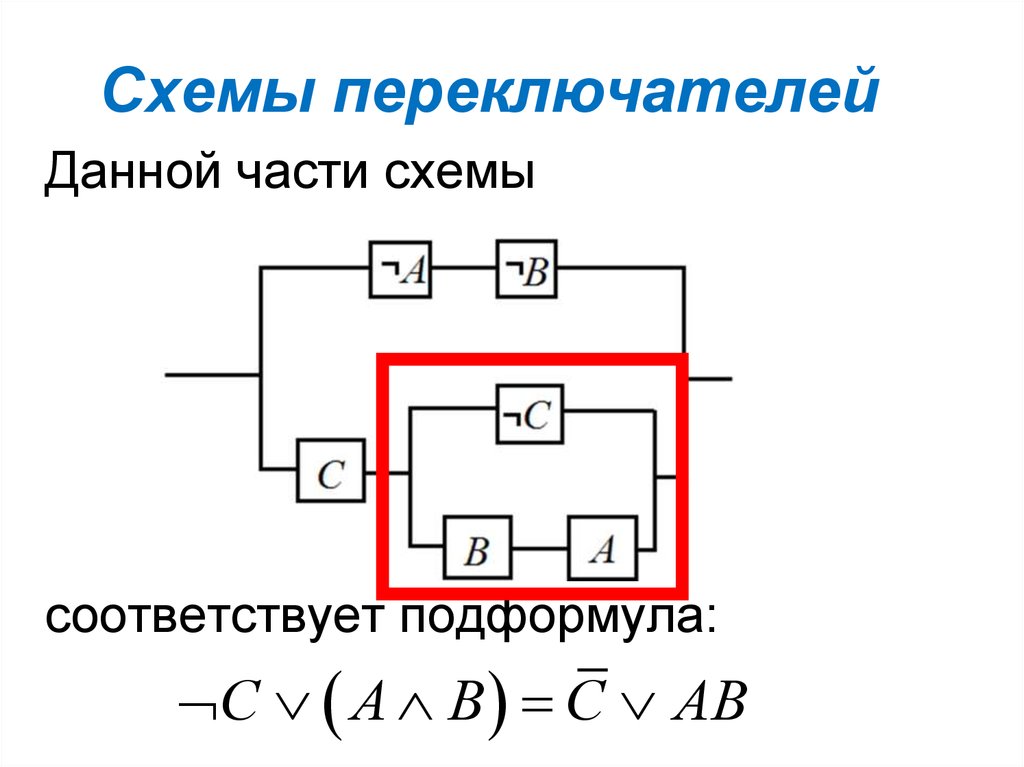
19. Схемы переключателей
Данной части схемысоответствует подформула:
С А В С АВ
20. Схемы переключателей
Данной части схемысоответствует подформула:
С С А В С С АВ
21. Схемы переключателей
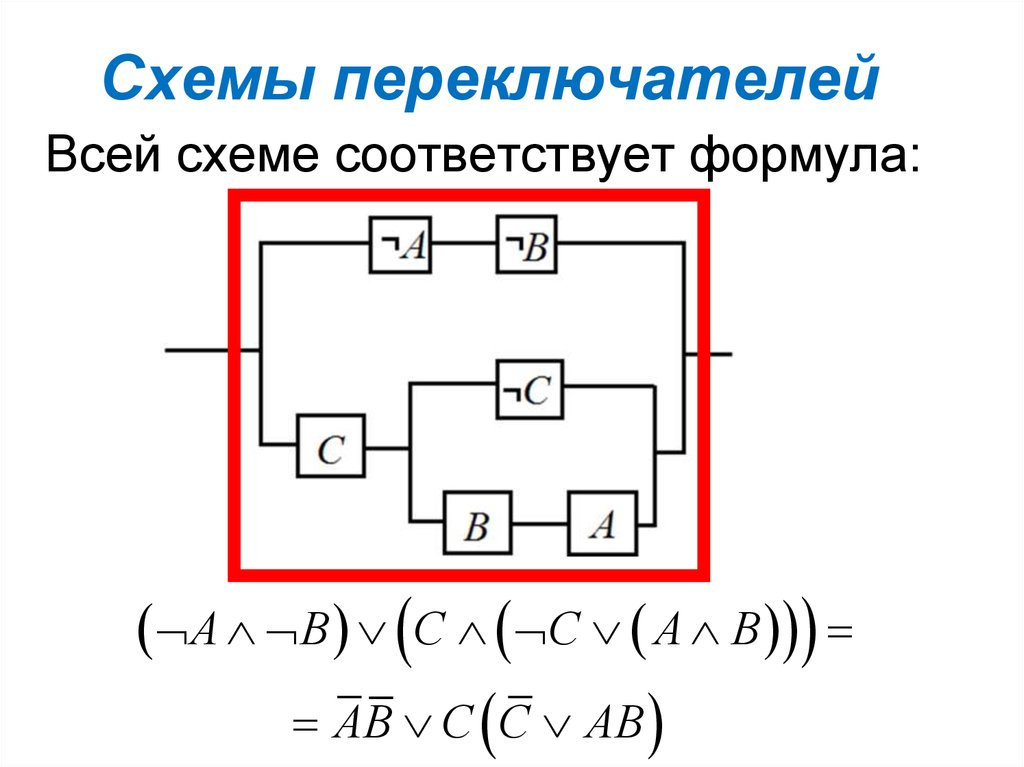
Всей схеме соответствует формула:А В С С А В
АВ С С АВ
22. Схемы переключателей
Упростим полученную булевуформулу.
АВ С С АВ АВ СС САВ
АВ САВ
Построим соответствующую схему
переключателей.
23. Схемы переключателей
АВ САВ24. Комбинационные схемы
Комбинационные элементы –электронные компоненты,
техническая реализация которых
может быть основана на
использовании различных
физических явлений: магнитных,
явлений в полупроводниках и т. д.
Они являются основными
компонентами компьютеров.
25. Комбинационные схемы
Все комбинационные элементыимеют один или более входов и
один выход. Каждый вход может
принимать одно из двух значений
(обычно низкое или высокое
напряжение).
Наиболее важные типы
комбинационных элементов
приведены в таблице 1.
26. Комбинационные схемы
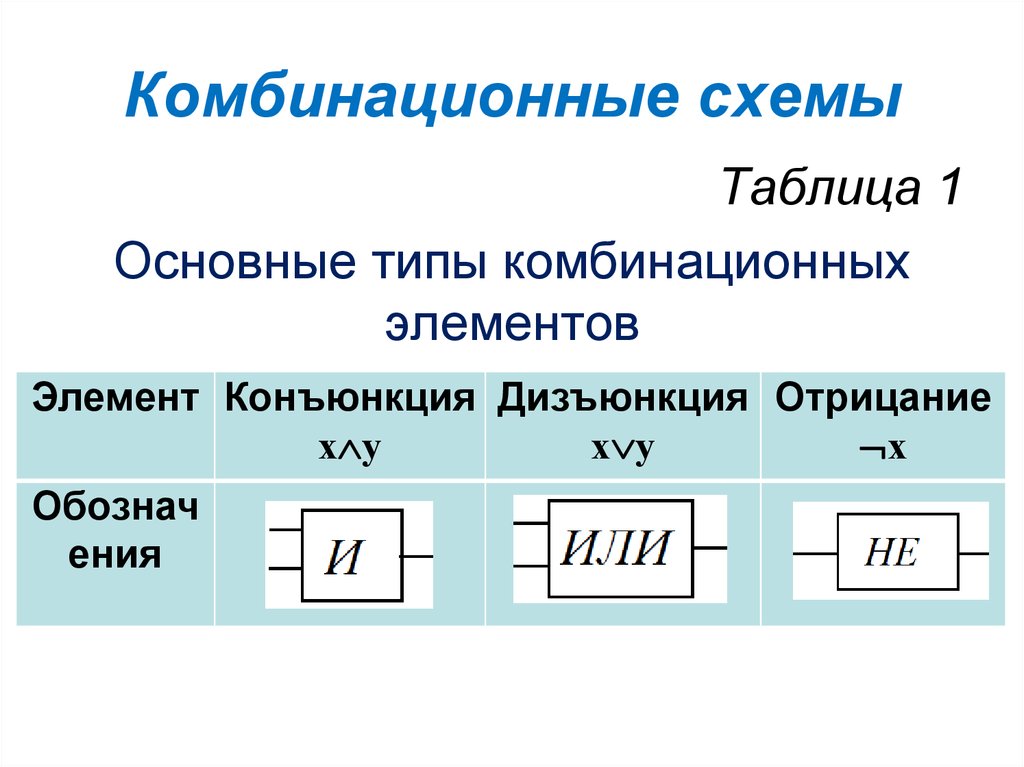
Таблица 1Основные типы комбинационных
элементов
Элемент Конъюнкция Дизъюнкция Отрицание
х у
х у
х
Обознач
ения
27. Комбинационные схемы
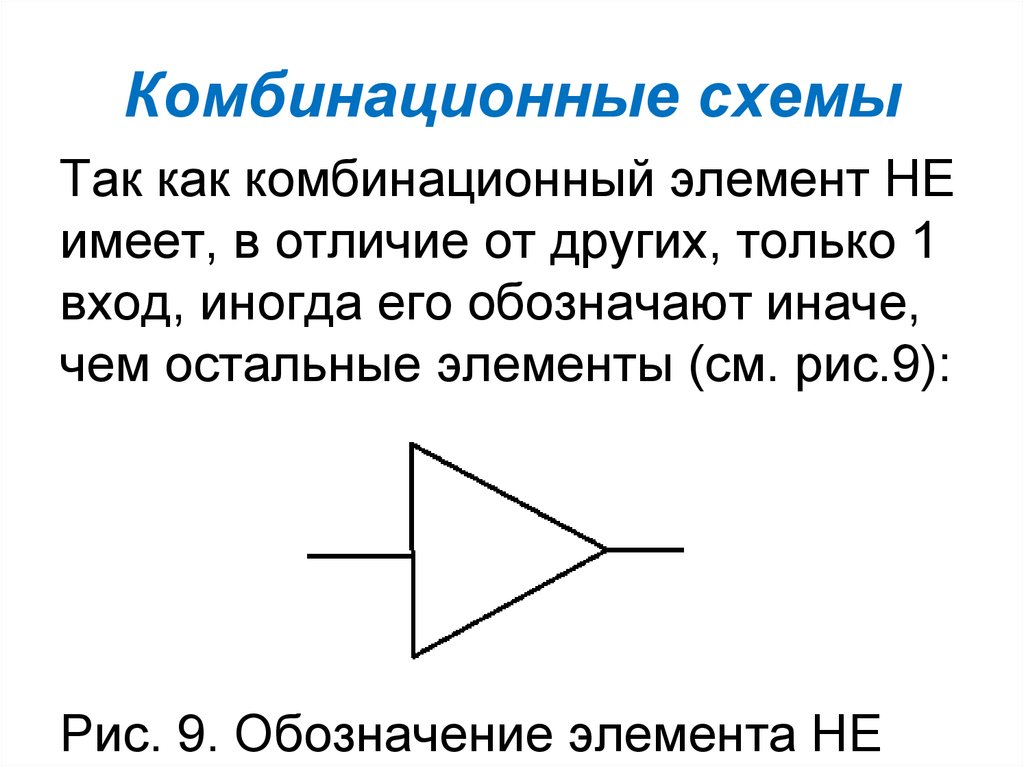
Так как комбинационный элемент НЕимеет, в отличие от других, только 1
вход, иногда его обозначают иначе,
чем остальные элементы (см. рис.9):
Рис. 9. Обозначение элемента НЕ
28. Комбинационные схемы
Различные комбинационныеэлементы могут быть связаны друг с
другом в цепи так, что выход одних
является входом других.
Такие цепи называются
комбинационными схемами
(логическими сетями).
29. Комбинационные схемы
Так как штрих Шеффера и стрелкаПирса являются функционально
полными системами, возможно
описание выходов комбинационных
схем с помощью каждого из этих
элементов.
30. Комбинационные схемы
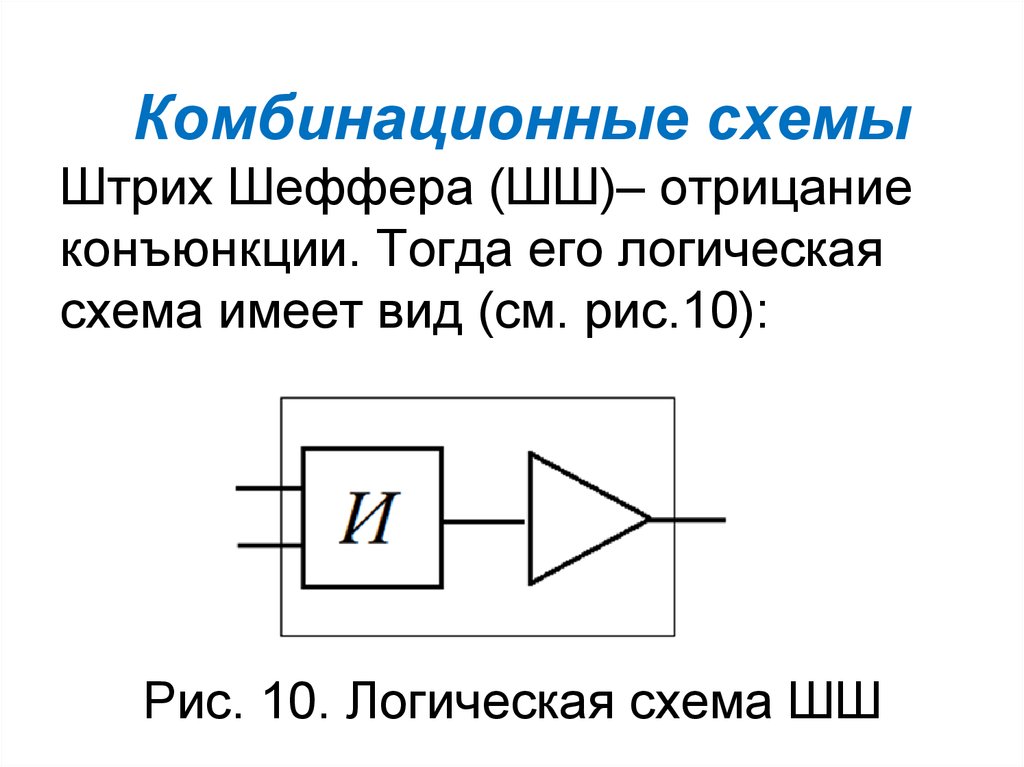
Штрих Шеффера (ШШ)– отрицаниеконъюнкции. Тогда его логическая
схема имеет вид (см. рис.10):
Рис. 10. Логическая схема ШШ
31. Пример
Записать формулу,соответствующую логической схеме,
приведенной на рисунке 11.
Рис.11. Логическая схема
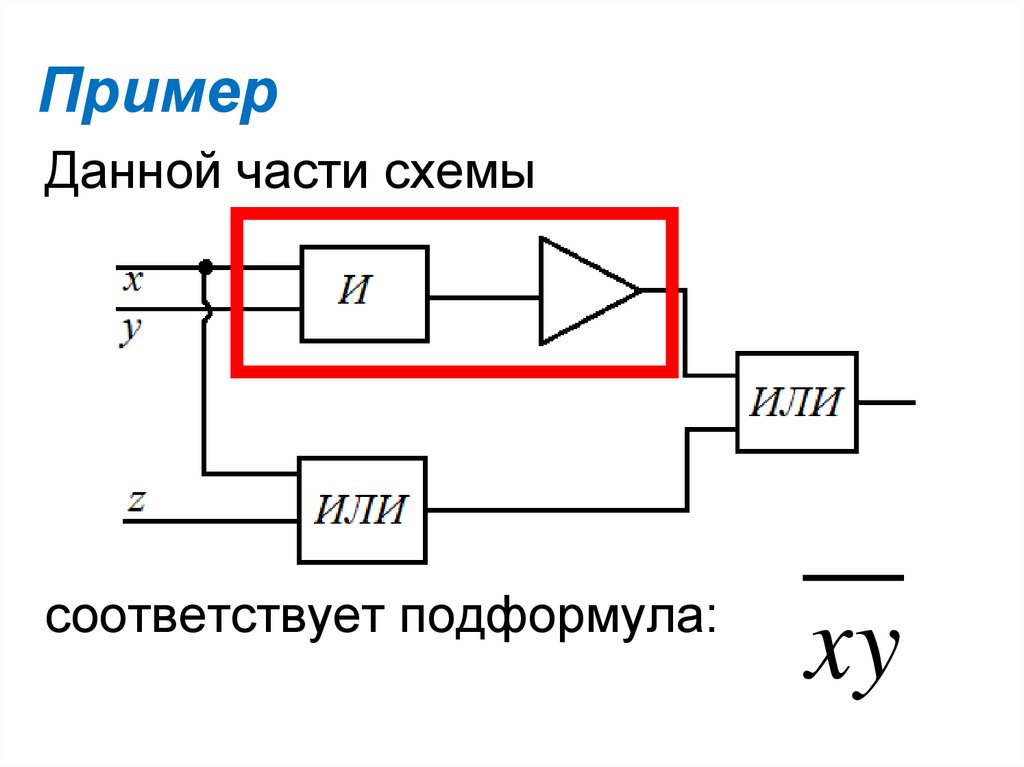
32. Пример
Данной части схемысоответствует подформула:
xy
33. Пример
Данной части схемысоответствует подформула:
x z
34. Пример
Всей схеме соответствует формулаf x, y, z xy x z
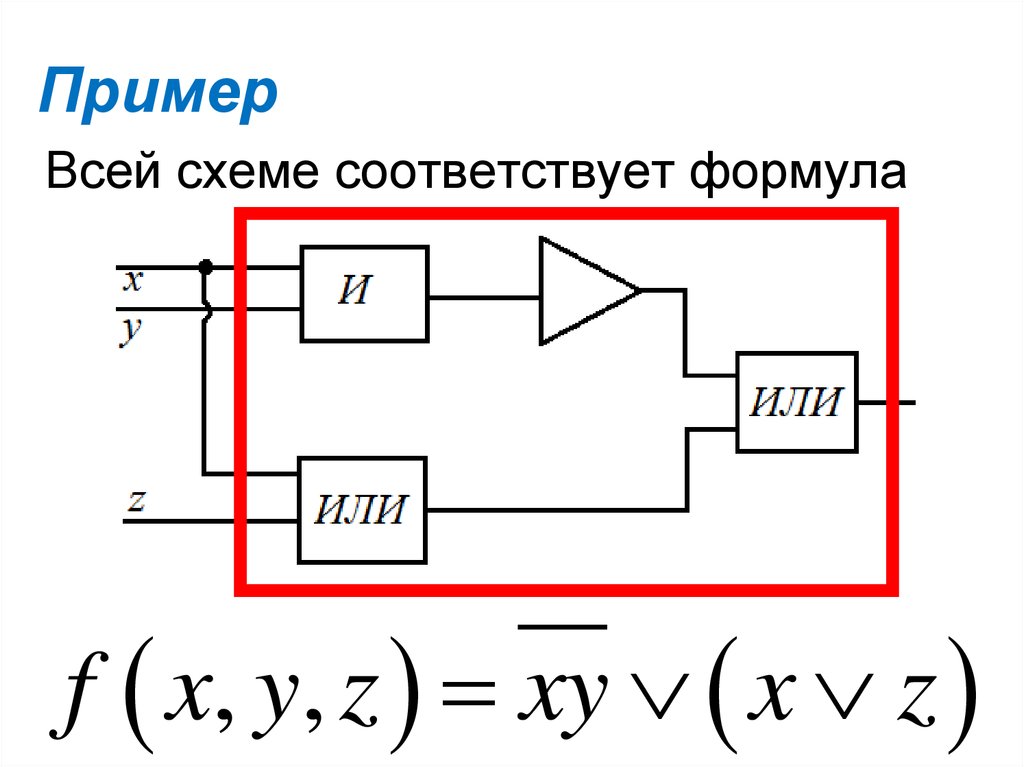
35. Пример
Иногда подформулы пишут насхеме. Получается скелет формулы.
xy
xy
f ( x, y, z )
x z





















 Математика
Математика








