Похожие презентации:
Две теоремы о функциональной полноте. ДМ.10
1. Дискретная математика
2.
Предполные классыФункционально полной называется такая система
функций , через функции которой можно выразить
любую логическую функцию.
Например, , , . Эта система функционально
полна, так как любая функция имеет булеву формулу.
Теорема.
Произвольная система будет функционально
полной, если она сводится к функционально полной
системе .
Это означает, что через функции системы можно
выразить все функции системы .
3.
Определение. Функция y f x1 , x2 , ... , xn сохраняет0, если y f 0, 0, ... , 0 0 .
Определение.
Функция
y f x1 , x2 , ... , xn
сохраняет 1, если y f 1,1, ... ,1 1.
y f x1 , x2 , ... , xn
Определение.
Функция
монотонная, если для любых двух наборов значений
аргументов и τ, таких что ≤ τ выполняется f( ) ≤ f(τ).
4.
Утверждение 1. Класс Т0 – функций, сохраняющих0, замкнут.
Утверждение 2. Класс Т1 – функций, сохраняющих
1, замкнут.
Утверждение 3. Класс S – самодвойственных
функций замкнут.
Утверждение 4. Класс L – линейных функций
замкнут.
5.
Теорема о булевой формуле монотоннойфункции. У каждой булевой формулы, отличной от 0 и
1 существует булева формула без отрицаний. Каждая
булева формула без отрицаний описывает монотонную
функцию, отличную от 0 и 1.
Что бы проверить, есть ли у данной функции булева
формула без отрицаний, достаточно построить ее
сокращенную ДНФ. Если она содержит отрицания,
значит, булевой формулы без отрицаний у этой
функции
не
существует.
Следовательно,
она
немонотонна.
Утверждение 5. Класс М – монотонных функций
замкнут.
6.
Лемма 1.Если функция y f ( x1 , x 2 , ... , x n ) – немонотонна,
то подстановкой n - 1 константы из нее можно получить
отрицание.
Доказательство. Пусть функция y f x1 , x2 , ... , xn
- немонотонна. Тогда существуют два набора
аргументов и τ, таких что ≤ τ, при этом f( ) > f(τ).
Пусть
набор
= ( 1, 2, …, n),
τ = (τ1, τ2, …, τn), причем f( ) = 1, а f(τ) = 0.
набор
Образуем цепочку соседних наборов, переводящих
в τ:
= δ1 ≤ δ2 ≤ … δk-1 ≤ δk = τ.
7.
Среди этих наборов есть δi ≤ δi+1 , которыеотличаются лишь в одной координате 0 и 1 . Но
i
i+1
при этом f(δ ) = 1, а f(δ ) = 0. Остальные координаты
этих наборов одинаковы. Если подставить значения
остальных координат вместо n - 1 переменной функции
y f x1 , x2 , ... , xn .
Функция
оставшейся
одной
переменной является отрицанием:
i
j
i
i
g(x ) = x .
i 1
j
8.
Лемма 2.Если функция y f x1 , x2 , ... , xn – нелинейна, то
подстановкой n - 2 констант из нее можно получить
дизъюнкцию и конъюнкцию.
Доказательство. Пусть y f x1 , x2 , ... , xn –
нелинейна. Тогда в ее полиноме Жегалкина есть
конъюнкция различных переменных. Обозначим эту
конъюнкцию K xi xi ...xi . Подставим вместо
1
2
k
переменных xi3 , xi4 , ..., xik единицу, вместо
переменных, не вошедших в конъюнкцию K – нули.
9.
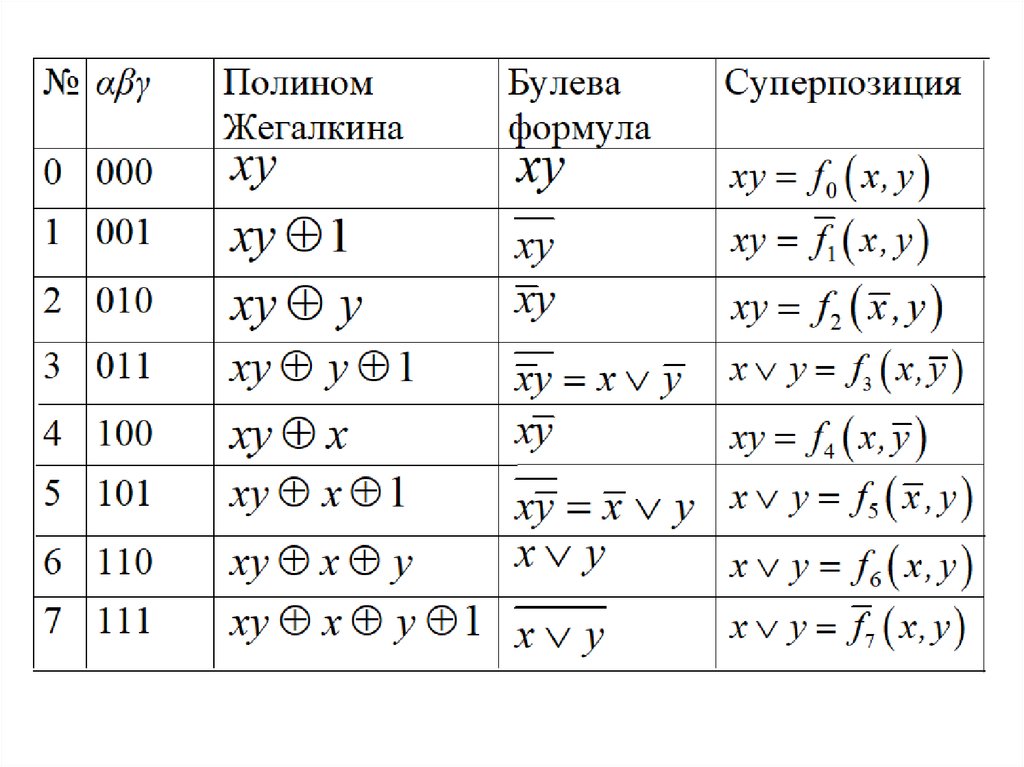
Заменим xi1 x, xi2 y . Полином Жегалкина приметвид:
xy x y .
В зависимости от вида функции y f x1 , x2 , ... , xn
коэффициенты α, β и γ могут принимать различные
значения. Покажем, что в каждом случае суперпозиция
полученной функции и отрицания будет являться
конъюнкцией
или
дизъюнкцией
переменных
xi1 x, xi2 y .
10.
11.
Теорема 1 о функциональной полноте.Для того чтобы система функций была
функционально полна в слабом смысле, необходимо и
достаточно, чтобы она содержала хотя бы одну
немонотонную и хотя бы одну нелинейную функцию.
Лемма 3.
y f ( x1 , x 2 , ... , x n )
Если
функция
–
несамодвойственна, то подстановкой отрицания из нее
можно получить константы 0 и 1.
12.
Теорема 2 о функциональной полноте (теоремаПоста).
Для того чтобы система функций
была
функционально полна (в сильном смысле), необходимо
и достаточно, чтобы она содержала
хотя бы одну немонотонную,
хотя бы одну нелинейную,
хотя бы одну несамодвойственную,
хотя бы одну не сохраняющую 0,
хотя бы одну не сохраняющую 1 функцию.











 Математика
Математика








