Соединения с повторениями

1.

06.04.2019
Тема №3.
Соединения с повторениями
"Число, положение и комбинация –
три взаимно пересекающиеся, но
различные сферы мысли, к которым
можно отнести все математические идеи".
Дж. Сильвестр
(1814 — 1897)
Лицей ИГУ,
liguirk.ru
Лавлинский М.В., [email protected]

2.

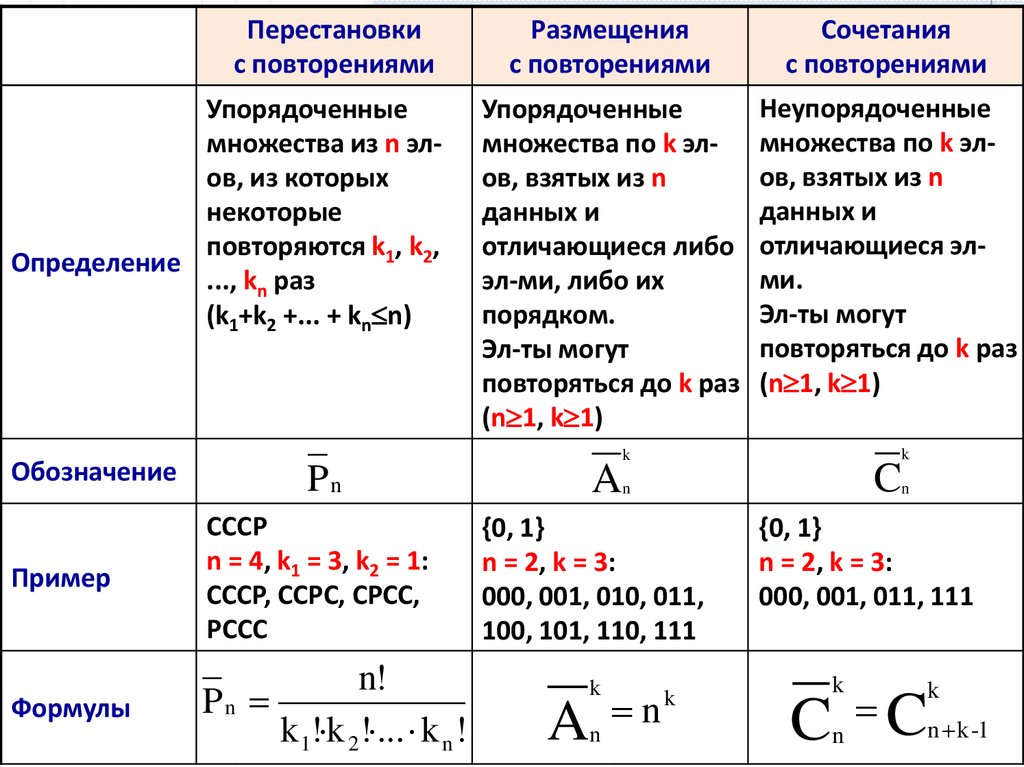
Перестановки
с повторениями
Упорядоченные
множества из n элов, из которых
некоторые
повторяются k1, k2,
Определение
..., kn раз
(k1+k2 +... + kn n)
Обозначение
Размещения
с повторениями
Сочетания
с повторениями
Упорядоченные
множества по k элов, взятых из n
данных и
отличающиеся либо
эл-ми, либо их
порядком.
Эл-ты могут
повторяться до k раз
(n 1, k 1)
Неупорядоченные
множества по k элов, взятых из n
данных и
отличающиеся элми.
Эл-ты могут
повторяться до k раз
(n 1, k 1)
k
k
A
Pn
Пример
CCCP
n = 4, k1 = 3, k2 = 1:
CCCP, CCPC, CPCC,
PCCC
Формулы
n!
Pn
k1! k 2 ! ... k n !
C
n
n
{0, 1}
n = 2, k = 3:
000, 001, 010, 011,
100, 101, 110, 111
k
A
n
n
k
{0, 1}
n = 2, k = 3:
000, 001, 011, 111
k
k
n
n k -1
C C

3.

Задача №1.
Сколько различных «слов» можно составить из слова
«ЛАОКООН», если каждое «слово» содержит семь букв,
и разрешается в каждом слове использовать буквы Л, А,
К и Н по одному разу, а букву О — три раза?
Дано:
U = (Л,А,О,К,О,О,Н)
n = 7,
kЛ=1, kА=1, kК=1,
kН=1, kО=3,
Найти:
N=?
Решение:
N Pn
n!
k Л ! k А ! k К ! k Н ! k О !
7!
4 5 6 7 840
1! 1! 1! 1! 3!
Ответ: 840

4.

Задача №2.
Сколько разных «слов» из четырех букв можно
составить из слова «мама»?
Дано:
U = (М,А,М,А)
n = 4,
kМ=2, kА=2
Найти:
N=?
Решение:
N Pn
1)
2)
3)
4)
5)
6)
4!
n!
6
k М ! k А ! 2! 2!
МАМА
АМАМ
ММАА
ААММ
МААМ
АММА
Ответ: 6

5.

Задача №3.
Сколько «слов» по две буквы можно составить из трех
букв: F, T, C?
Дано:
U = {F, T, C}
n = 3,
k=2
Найти:
N=?
Решение:
k
n
N A n 3 9
1)
2)
3)
4)
5)
6)
7)
8)
9)
FT
TF
FC
CF
TC
CT
FF
TT
CC
k
2
Ответ: 9

6.

Задача №4.
Сколько «слов» по три буквы можно составить из двух
букв E и N?
Дано:
U = {E, N}
n = 2,
k=3
Найти:
N=?
Решение:
k
n
N A n 23 8
1)
2)
3)
4)
5)
6)
7)
8)
EEE
EEN
ENE
ENN
NEE
NEN
NNE
NNN
k
Ответ: 8

7.

Задача №5.
В школьной столовой на десерт дают яблоки и груши. В
комплект входит три плода по выбору школьника.
Сколько разных вариантов десерта возможно?
Дано:
Решение:
k
3
U = {Я, Г}
k
4!
4
n
n k -1
n = 2,
3! 1!
k=3
N C C
C
N 4
Найти:
N=?
1)
2)
3)
4)
ЯЯЯ
ЯЯГ
ЯГГ
ГГГ
Ответ: 4

8.

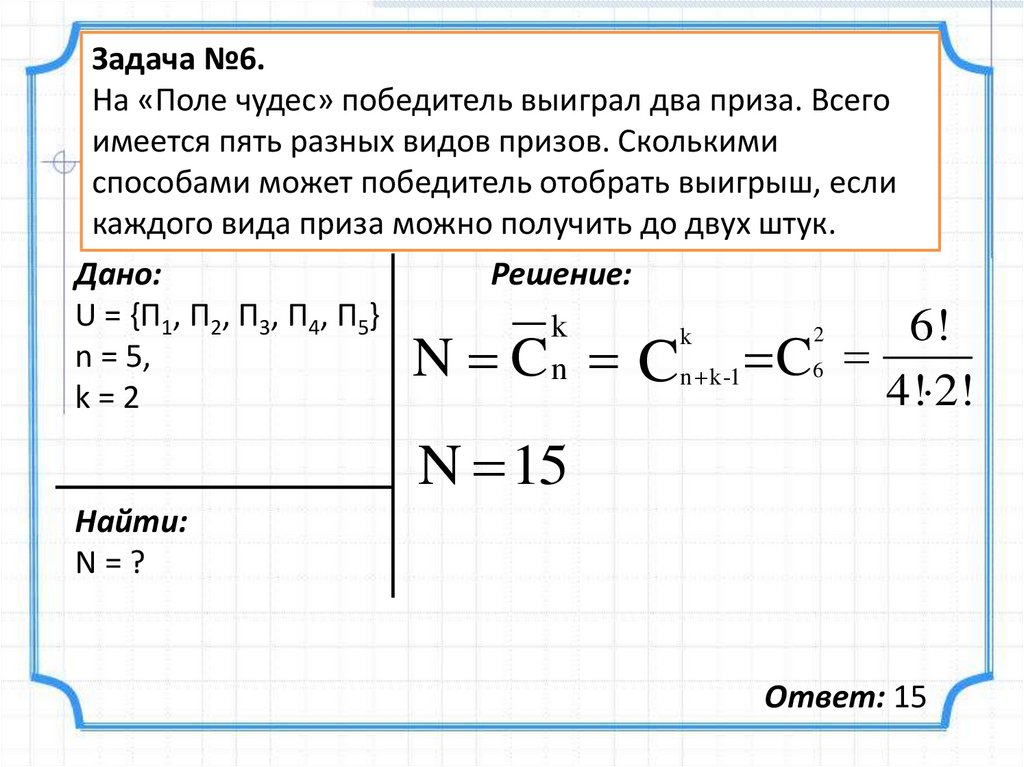
Задача №6.
На «Поле чудес» победитель выиграл два приза. Всего
имеется пять разных видов призов. Сколькими
способами может победитель отобрать выигрыш, если
каждого вида приза можно получить до двух штук.
Дано:
Решение:
U = {П1, П2, П3, П4, П5}
k
6!
2
k
n = 5,
6
n
n k -1
4! 2!
k=2
N C C
C
N 15
Найти:
N=?
Ответ: 15

9. Домашнее задание

06.04.2019
Домашнее задание
1. «3_Соединения с повторениями [ДЗ].doc»
Лицей ИГУ, liguirk.ru