Похожие презентации:
Элементы комбинаторики. (Лекция 1)
1.
Теория вероятностей иматематическая статистика
Доц.Лаптева Надежда Александровна
Лекция 1
§1. Элементы комбинаторики.
Комбинаторика изучает число
комбинаций из предметов.
1. Перестановки Pn = n ! - важен только
порядок.
Пример. Сколькими способами можно
расставить 5 различных книг на полке?
5 × 4 × 3 × 2 ×1 = 5!
2.
2. Размещенияn!
A =
(n - m)!
m
n
-- важен порядок.
Пример. Всего 10 цифр. Сколькими
способами можно составить
трехзначный номер?
10! 7!× 8 × 9 ×10
A =
=
= 8 × 9 × 10 = 720
7!
7!
3
10
3.
3.Сочетанияn!
C =
m!( n - m)!
m
n
Разные предметы, порядок не важен.
Пример. В группе 20 человек.
Сколькими способами можно выбрать
трех делегатов на конференцию?
20! 17!×18 ×19 × 20
C =
=
= 1140
3!17!
1 × 2 × 3 ×17!
3
20
4.
4.Размещения с повторениями.Все важно – и порядок, и предметы,
причем их можно повторять.
m
n
A =n
m
5.
2. Случайные события.Определение 1. Событие называется
случайным, если оно может произойти,
а может не произойти. Обозначение
событий -- A, B, C ,...
Пример 1. Бросаем монету. Событие
«выпадет герб» является случайным.
Пример 2. Бросаем кубик. Цифры
1,2,3,4,5,6 – случайны.
6.
Кубик будем называть игральной костью.Испытание – это создание условий для
возможного события. Например, бросить
кость, бросить монету и т.д.
Определение 2. Два события называются
несовместными, если они не могут
произойти вместе.
Пример. Бросаем монету. Герб или цифра
--- несовместные события.
7.
Определение 3. Пусть задана системаиз нескольких случайных событий. И
пусть все они попарно несовместны.
Пусть при испытании обязано
появиться одно и только одно из них.
Тогда говорят, что задана полная
группа событий.
8.
Пример 1. Герб и цифра --- полнаягруппа при бросании монеты.
Пример 2. Кубик с шестью гранями
состоит из шести цифр, то есть на
каждой грани написана одна цифра.
Эти цифры --- полная группа событий.
9.
Определение 4. Пусть задана полнаягруппа из n событий A, B,..., M .
И пусть ни одному из них не отдается
предпочтения.
Тогда события называют
равновозможными и каждому
приписывают его долю как вероятность
1
p= .
n
10.
События из полной группынесовместных событий часто называют
элементарными.
Из элементарных событий составляют
более сложные события --- составные.
11.
Если событие A состоит изнескольких элементарных, то
составляющие его элементарные
события называют благоприятными.
Их число обозначим m.
Общее число всех элементарных
событий в полной группе
равновозможных событий обозначим
n.
12.
Классическое определение вероятности.Пусть имеется полная группа
равновозможных несовместных
событий. Их число n. И пусть
случайное событие A состоит из
элементарных событий.
Тогда
m
P ( A) = .
n
m
13.
Частные случаи1.Всегда
0 £ P ( A) £ 1.
2. Событие называется невозможным,
если оно не может произойти. Тогда
m 0
P (0) = = = 0.
n n
(m( A) = 0, так как ни одно из
событий ему не благоприятствует).
Следствие 1. Вероятность невозможного
события равна нулю.
14.
3. Достоверное событие E --- всегдапроисходит. Ему благоприятствуют все
элементарные события, то есть
m( E ) = n.
Тогда
P ( E ) = 1.
Следствие 2. Вероятность достоверного
события равна единице.
15.
Следствие 3. Вероятность любогослучайного события заключена между
нулем и единицей:
0 £ P ( A) £ 1.
16.
AДоказательство. Если
--- случайное
событие из m элементарных
событий, то число m £ n --- общего
их числа, поэтому
m
P ( A) = £ 1.
n
Это положительное число, поэтому
m
P ( A) = ³ 0.
n
17.
Примеры непосредственноговычисления вероятностей случайных
событий.
Формула
m
P ( A) = .
n
18.
Пример 1. Брошена игральная кость.Какова вероятность выпадения простого
числа?
Перечислим все простые числа от 1 до 6.
Это 1,2,3,5.
4 2
m( A) = 4, n = 6, P ( A) = = .
6 3
19.
Пример 2. Брошен кубик два разаподряд. Какова вероятность, что оба
раза выпадут четные числа?
Событие A --- выпали четные числа.
2,4,6 --- оба раза.
n = 6 × 6 = 36 событий. На каждую
цифру №1 есть 6 возможностей цифры
№2.
20.
Правило умножения.Если комбинация A состоит из k
вариантов, каждый вариант состоит из
l других вариантов B, то пара ( A, B )
состоит из k × l вариантов.
21.
Вычислимпары
2,2
4,2
6,2
m( A) , то есть перечислим
2,4
4,4
6,4
m = 9.
9 1
P ( A) =
= .
36 4
2,6
4,6
6,6
22.
Лекция №2Геометрическая вероятность
На прошлой лекции было введено
классическое определение
вероятности. Еще в начале развития
теории вероятностей была замечена
недостаточность этого определения,
так как оно предполагает конечное
число исходов. Легко придумать
пример с бесконечным числом
исходов.
23.
Например, попадание иглы в точкуотрезка. Подобные задачи приводят к
понятию геометрической вероятности.
Задача. В так называемый “квадрат
рассеяния” со стороной 60 метров
падают снаряды. Считаем, что
попадание во все точки квадрата
равновероятно. В квадрате находится
мост размером 30 метров на 20 метров.
Какова вероятность попасть в мост?
24.
S260
20
S1
30
25.
Здесь S1 -- площадь моста, а-- площадь квадрата.
S2
Решение: мост занимает полосу
1
шириной
3
1
длиной
2
от стороны квадрата и
от стороны квадрата.
26.
Таких полос на квадрате находится 6.Считаем, что попадание в каждую такую
полосу равновероятно и равно
S1
P ( A) = .
S2
27.
Определение. Пусть даны двамножества A Ì K .
Считаем, что всегда попадаем в
множество K . Тогда вероятность
попасть в множество A равна
SA
P ( A) =
.
SK
28.
mes AОбобщение: P ( A) =
.
mes K
K = [ a, b] ;
A = [a , b ];
b -a
P ( A) =
.
b-a
29.
Такая вероятность называетсягеометрической вероятностью и
приписывается множеству любой
размерности.
Замечание. Каждая область
состоит из точек. Пусть A
-точка. Какова вероятность попасть
в точку
P ( A)?
Так как любая мера точки есть
нуль, то
P ( A) = 0.
30.
Такие события называютсяневозможными.
Итак, бросая иглу, мы попадем в точку,
но вероятность попадания в точку есть
нуль, то есть событие невозможное.
Приведенное противоречие – один из
примеров «парадоксов бесконечности».
31.
Пример. В круге радиуса R наудачупоявляется точка.
Определить вероятность того, что она
попадает в одну из двух
непересекающихся фигур, площади
которых равны S , S .
1
2
S1 + S2
P ( A) =
.
2
pR
32.
Задача о встрече.Два лица условились встретиться в
определенном месте между 12 и 13
часами. Пришедший первым ждет
другого в течение 20 минут, после чего
уходит. Чему равна вероятность
встречи лиц A и B ?
Если приход каждого из них может
произойти наудачу и моменты прихода
независимы.
33.
Решение. Обозначим моментыприхода лица A через x
и лица B через y.
Для того, чтобы встреча произошла,
необходимо, чтобы
x - y £ 20.
34.
Станем изображать x , y каккоординаты на плоскости, в качестве
единицы масштаба выберем минуту.
y
20
0
20
60 x
35.
Благоприятные исходы расположены взаштрихованной области.
S = 60 - 40 ;
2
2
60 - 40
5
P ( A) =
=
.
2
60
9
2
2
36.
Операции надслучайными событиями
Геометрическое определение
вероятности дает возможность
привлечь множества и операции над
ними, именно, объединение и
пересечение.
37.
Напомню:AÈ B = C
A
AÇ B = D
B
38.
Определение 1. Пусть A, B Ì K .Суммой случайных событий A + B
называется третье событие C ,
состоящее в наступлении хотя бы
одного из первых двух событий.
Определение 2.
Произведением случайных
событий A × B называется третье
событие D , состоящее в
наступлении как события A, так и B.
39.
Лекция №3Операции над случайными событиями
1. Формула сложения вероятностей
Рассмотрим площадь S ( A + B ).
S ( A + B ) = S ( A) + S ( B ) - S ( AB ).
A
B
40.
K.mes(
A
+
B
)
Тогда, так как P ( A + B ) =
,
получаем
mes K
P ( A + B ) = P ( A) + P ( B ) - P ( AB ).
Разделим обе части на площадь
Это формула сложения вероятностей.
Если AB
то есть
= Æ, то P ( AB ) = 0,
P ( A + B ) = P ( A) + P ( B ).
41.
Определение. Для несовместныхсобытий формула сложения
вероятностей принимает вид
P ( A + B ) = P ( A) + P ( B ).
Следствие. Введем событие A,
противоположное событию A.
Тогда A + A = D, где
D -- достоверное событие.
Следовательно,
P ( A + A) = P ( A) + P ( A) = 1.
P ( A) = 1 - P ( A).
42.
Пример. Стрелок производитвыстрел по мишени, состоящей из
двух колец: 10 и 9. Вероятность
попадания в 10 равна P ( A) = 0,1.
Вероятность попадания в 9 равна
P ( B ) = 0,2.
Какова вероятность попасть в
мишень?
P ( A + B ) = 0,1 + 0,2 = 0,3.
43.
2. Условная вероятность.PB ( A) означает вероятность
события A при условии, что событие
произошло.
Пример. Брошены две игральные
кости. Чему равна вероятность, что
сумма выпавших очков равна 8
(событие A ), если известно, что
выпадает четное число (событие B )?
B
44.
Рассмотрим все благоприятные исходы2+6
6+2
4+4 3+5 5+3
Всего исходов 36. Благоприятных
исходов 5. Но если произошло
событие B, то всех исходов будет
не 36, а 18.
Таким образом,
5
PB ( A) = .
18
45.
Для условной вероятностиP ( AB )
PB ( A) =
P( B)
или
P ( AB ) = PB ( A) × P ( B).
Если события A и B независимы,
то
PB ( A) = P ( A).
Тогда
P ( AB ) = P ( A) P ( B ).
46.
Пример. Два стрелка независимо другот друга стреляют по цели.
Вероятность попадания для первого
p1 = 0,8; для второго p2 = 0,7.
Найти вероятности следующих
событий.
А) оба стрелка попадут в цель.
P ( A) = p1 × p2 = 0,8 × 0,7 = 0,56.
47.
В) только один попадет в цель.Это значит, что первый попадает и
второй не попадает или наоборот, то
есть второй попадает и первый не
попадает. В этом случае
P ( B ) = p1 × (1 - p2 ) + p2 (1 - p1 );
P ( B ) = 0,38.
48.
С) Хотя бы один попал в цель.Рассмотрим противоположное
событие: оба не попали в цель.
P (C ) = (1 - p1 )(1 - p2 );
P (C ) = 0,2 × 0,3 = 0,06;
P (C ) = 1 - P (C ) = 0,94.
49.
3. Формула полной вероятностиПусть даны два события A
и B,
причем B является суммой новых
событий:
B = H1 + H 2 + ... + H n .
Тогда
AB = AH1 + ... + AH n .
50.
Предполагается, что событияH1 , H 2 ,..., H n
несовместны.
Тогда события AH1 ,..., AH n также
несовместны, как части несовместных
событий.
Тогда
P ( AB ) = P ( AH1 ) + ... + P ( AH n );
n
P ( AB ) = å PH k ( A) × P ( H k ).
k =1
51.
Так как P ( AB ) = P ( A), тополучаем формулу, которая называется
формулой полной вероятности
n
P ( A) = å PH k ( A) × P ( H k ).
H1, ..., H n
k =1
называются гипотезами.
Гипотез должно быть столько, чтобы
они обеспечили все возможные
результаты испытаний.
52.
Пример. В группе спортсменов5 лыжников,
6 велосипедистов и
4 бегуна.
Вероятность выполнить
квалификационную норму:
для лыжника – 0,9;
для велосипедиста – 0,8;
для бегуна – 0,75.
Найти вероятность, что спортсмен,
выбранный наудачу, выполнит норму.
53.
Введем событиеA --- спортсмен выполнит норму.
Гипотезы:
H1 --- лыжник,
H 2 --- велосипедист,
H --- бегун.
3
54.
5P ( H1 ) = ;
15
6
P( H 2 ) = ;
15
4
P( H 3 ) = .
15
PH1 ( A) = 0,9; PH 2 ( A) = 0,8;
PH3 ( A) = 0,75.
55.
P ( A) = PH1 ( A)× P ( H1 ) ++ PH 2 ( A)× P ( H 2 ) + PH3 ( A)× P ( H 3 );
P ( A) = 0,82.
56.
4. Повторные испытания.Формула Бернулли
A
P ( A) = p.
с
известной
вероятностью
Введем
событие
A, P ( A) = q,
причем q = 1 - p.
Пусть имеется только одно событие A.
Пусть дано случайное событие
Но из него можно сделать
сколько угодно событий путем
повторения.
57.
Например, стреляя в одну мишень,можем получить
A × A × A (попал, не попал, попал).
Получилось новое событие, которое
называется повторным испытанием.
P ( A × A × A) = p q.
2
58.
Обобщим приведенный пример,произведя n испытаний.
При этом будем считать, что событие
наступило
раз.
k
Например,
B1 = A... AA... A,
P ( B1 ) = p q
k
n-k
.
A
59.
Однако, событие A может появлятьсяи в другой последовательности
B2 = AA... AA... AAA,
а может и в другой.
Всего получается
C
k комбинаций.
n
60.
Теорема. Вероятность того, что всерии из n испытаний событие
A появится k раз, вычисляется
по формуле Бернулли
Pn ( k ) = C × p × q
k
n
k
n- k
, q = 1 - p.
61.
Вероятность того, что событие Aпроизойдет не менее k раз в серии
из n опытов, вычисляется по формуле
n
Pn (³ k ) = å C p q
m= k
m
n
m
n-m
.
62.
Пример. Какова вероятность, что в семье,имеющей 5 детей, будут 2 мальчика?
Вероятности рождения детей считать
одинаковыми.
1
1
p = , q = ; n = 5, k = 2.
2
2
10 5
2
2
3
P5 (2) = C5 (0,5) (0,5) =
= .
32 16
63.
Лекция №4Локальная и интегральная
теоремы Лапласа
На прошлой лекции мы вывели
формулу Бернулли
Pn ( k ) = C p q
Если числа n и k
k
n
k
n -k
.
велики, то
вычисления становятся громоздкими.
В этом случае можно воспользоваться
приближенной формулой Лапласа.
64.
Теорема 1 (локальная теорема Лапласа).1
k - np
Pn ( k ) =
j ( x ), x =
,
npq
npq
- x2
где
1
2
j ( x) =
e .
2p
Замечание. Формула Лапласа тем
точнее приближает формулу Бернулли,
чем больше число n (более
нескольких десятков) и np > 10.
65.
Теорема 2 (интегральная теорема Лапласа).Вероятность
того, что
Pn ( k1 , k2 )
событие A наступит от k до k раз в
1
2
серии из n одинаковых независимых
испытаний приближенно вычисляется по
формуле Лапласа
Pn ( k1 , k2 ) » F( x2 ) - F( x1 ),
66.
xt2
2
1
F( x ) =
e
dt
ò
2p 0
k1 - np
k2 - np
x1 =
; x2 =
.
npq
npq
F( - x ) = -F( x ).
Для
x>5
можно считать
F( x ) = 0,5.
67.
Пример 1. Вероятность поражениямишени при одном выстреле равна 0,8.
Найти вероятность того, что при 100
выстрелах мишень будет поражена
ровно 75 раз.
Решение. Воспользуемся локальной
формулой Лапласа
1
k - np
Pn ( k ) =
j ( x ), x =
;
npq
npq
68.
Тогдаn = 100; p = 0,8;
k = 75; q = 0,2.
По таблице 1 находим
j (1,25) = 0,1826.
Следовательно,
P100 (75) = 0,04565.
69.
Пример 2. Вероятность поражения мишенипри одном выстреле равна 0,8.
Найдите вероятность того, что при 100
выстрелах мишень будет поражена не
менее 75 и не более 90 раз.
Решение. Воспользуемся интегральной
формулой Лапласа.
æ k2 - np ö
æ k1 - np ö
Pn ( k1 , k2 ) = F ç
÷ - Fç
÷,
è npq ø
è npq ø
где F ( x ) --- функция Лапласа.
70.
n = 100; p = 0,8; q = 0,2;k1 = 75; k2 = 90.
P100 (75,90) = F(2,5) - F( -1,25) =
= F(2,5) + F(1,25) = 0,8882.
Значения функции F ( x ) находим по
таблице 2.
Запомните:
F( - x ) = -F( x ).
71.
3.Формула Пуассона.Пусть p --- вероятность события A
Тогда вероятность
наступления
вPкаждом
испытании. события A
(
k
)
n
ровно k раз в серии из n испытаний
вычисляется по формуле Пуассона
k -l
где
l e
Pn ( k ) »
,
k!
l = np.
72.
Замечание. Формула Пуассона темточнее, чем меньше p и больше n,
причем np < 10.
Пример. Учебник издан тиражом 100000
экземпляров. Вероятность того, что
учебник сброшюрован неправильно,
равна 0,0001. Найти вероятность того,
что тираж содержит ровно 5
бракованных книг.
73.
По условиюn = 100000; p = 0,0001; k = 5.
Так как n велико, а p мало, то
воспользуемся формулой Пуассона
k -l
l e
Pn ( k ) =
, l = np = 10.
k!
5 -10
10 e
P100000 (5) =
» 0,0375.
5!
74.
Самостоятельная работаЗадача №1.
Найти вероятность того, что событие
наступит 1400 раз в 2400
испытаниях, если появления этого
события в каждом испытании равна
0,6.
Задача №2.AВероятность появления
события
в каждом из 100
независимых испытаний равна 0,8.
Какова вероятность, что событие
появится не более 74 раз?
A
75.
Лекция №5Дискретная случайная величина
Определение. Случайная величина X
называется дискретной, если в
результате испытания она принимает
одно из конечного или счетного
множества значений x1 , x2 , x3 ,K .
76.
Закон распределения или рядраспределения дискретной случайной
величины задается в виде таблицы
X x1 x2 K
P p1 p2 K
p1 + p2 + K = 1
77.
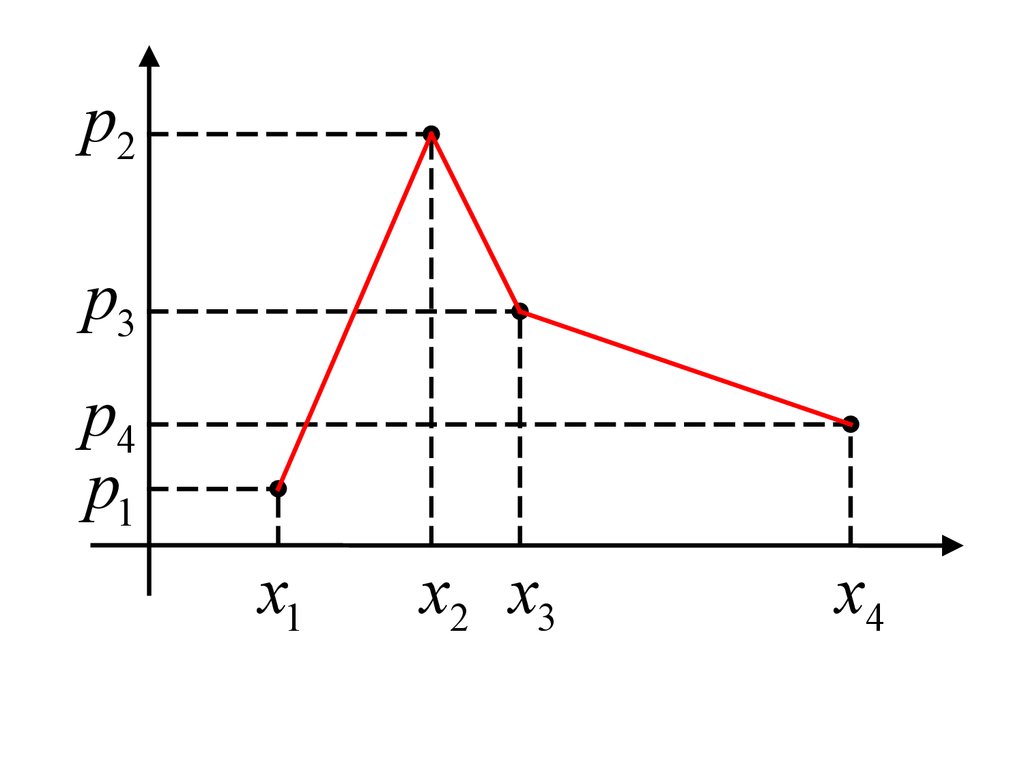
Многоугольник распределенияВ системе координат стоят точки
M i ( xi ; pi ),
i = 1, 2,K .
где
Соединяют эти точки последовательно
прямыми. Получают ломаную, которую
и называют многоугольником
распределения.
78.
p2p3
p4
p1
x1
x2 x3
x4
79.
Пример 1. Два стрелка стреляют по целипо одному разу. Вероятность попадания:
для первого стрелка 0,6;
для второго –
0,7.
Найдите закон распределения и постройте
многоугольник распределения.
80.
Пусть X -- число попаданий.X -- случайная величина, принимает
значения 0, 1, 2.
Найдем соответствующие вероятности.
Ноль попаданий:
(первый не попал и второй не попал)
P (0) = 0, 4 × 0,3 = 0,12.
81.
Одно попадание(первый попал и второй не попал, или
первый не попал и второй попал):
P (1) = 0,6 × 0,3 + 0, 4 × 0,7 = 0, 46.
Два попадания (первый попал и второй
попал): P (2) = 0,6 × 0,7 = 0, 42.
0
1
2
X
0,12
0,46
0,42
P
0,12 + 0, 46 + 0, 42 = 1.
82.
Многоугольник распределенияP
1
X
P
0
1
2
0,12
0,46
0,42
0, 46
0, 42
0,12
0
1
2 X
83.
Функция распределенияF ( x) = P( X < x)
F ( x) – функция распределения.
F ( x)
Свойства______
1) 0 £ F ( x ) £ 1;
F (-¥) = 0; F (+¥) = 1.
2) F ( x ) неубывающая функция на
(-¥; +¥).
3) P ( a < X < b) = F (b) - F ( a ).
84.
F ( x) определяется формулойx ,£ x1
ì 0,если
ï p ,если
x
<
x
£
,
x
1
1
2
ï
F ( x) = í
p1 + p2 ,если x2 < x £ x,3
ï
x .> xn
ïî 1,если
85.
График – ступенчатая функция.P
1
K
p1+ p2 + p3
p1+ p2
p1
0
x1
x2 x3 K
xn X
86.
Числовые характеристики дискретнойслучайной величины
Задача. Автомат режет гвозди из
проволоки. Всего 100 гвоздей. 50 гвоздей
длиной 10 см; 40 гвоздей – 9 см; 10
гвоздей – 11 см. Найти среднюю длину
гвоздя.
d ср.
10
×
50
+
9
×
40
+
11
×
10
=
=
100
50
+
36
+
11
97
=
=
= 9,7см.
10
10
87.
А теперь введем случайную величинуX – длина гвоздя. Составим ряд
распределения.
X
P
9
10
11
0,4
0,1
0,5
88.
Определение. Математическиможиданием случайной величины
называется число
X
M ( X ) = x1 × p1 + x2 × p2 +K + xn × pn .
Найдем M ( X ) в нашем примере:
M ( X ) = 9×0, 4 +10×0,1+11×0,5 = 9,7.
Таким образом
M ( X ) = d ср.
89.
СвойстваM (X )
M (C ) = C
2) M ( kX ) = kM ( X ) ( k – константа)
M ( X ) может принимать любое
1)
значение. Например, средняя
температура в Москве в феврале
X)
меньше нуля. Следовательно, M (может
быть и отрицательным, и равным нулю.
90.
ДисперсияПример.
X ,Y
– случайные величины:
X -2 -1 +1 +2
1
1
1
1
P 4 4
4 4
Y -20 -10 +10 +20
1
1
1
1
P 4 4
4 4
91.
Очевидно, M ( X ) = M (Y ) = 0. Норазбросы X , Y от среднего значения
разные.
Для характеристики разброса служит
дисперсия:
D ( X ) = M ( X - M ( X ) ) или
2
2
D ( X ) = M ( X ) - M ( X ).
2
M ( X ) = x × p1 + x × p2 +K + x × pn .
2
2
1
2
2
2
n
92.
Для нашего примера:1
2 1
D ( X ) = (-2) × + ( -1) × +
4
4
2 1
2 1
2
+ 1 × + 2 × - 0 = 2,5.
4
4
2 1
2 1
D ( X ) = (-20) × + (-10) × +
4
4
2 1
2 1
2
+ 10 × + 20 × - 0 = 250.
4
4
2
93.
Таким образом,а Y = 10 X .
D (Y ) = 100 × D( X ),
Чтобы улучшить характеристику
разброса, вводят среднее квадратичное
отклонение: (сигма)
s ( X ) = D( X ).
94.
СвойстваD( X )
D( X ) ³ 0;
2) D (C ) = 0, если C
1)
3)
D(kX ) = k D( X ),
постоянная.
2
– постоянная;
если
k
–
95.
Примеры законов распределения1) Биномиальный закон
Pn (k ) – вероятность появления
события A ровно k раз в n
испытаниях вычисляется по формуле
Бернулли
Pn (k ) = C × p × (1 - p )
k
n
k
n!
Напомню, C =
(n - k )!k !
k
n
n-k
.
(сочетания).
96.
2) Закон ПуассонаЕсли n велико, а вероятность p
появления события A в каждом
испытании очень мала, то
-l
e ×l
Pn (k ) =
,
k
!
l = np.
k
где
Тогда случайная величина X
распределена по закону Пуассона.
97.
28.02.11 Контрольная работа №1Аудитория
Дома
Стр
7
10
18
20
33
34
№
1,2,3,4
1.3
3,4
2.6
6
8
Рушайло М.Ф.
Стр
199
200
202
217
219
219
219
№
1
2,3
6
5,6
8
1
3
Жукова Г.С.
(часть II)
Стр
10
10
22
37
40
№
1.1
1.5
2.24
3.4
3.26(a)
Рушайло М.Ф.
Стр
205
206
219
222
№
1
13,14
3
19(a)
Жукова Г.С.
(часть II)
98.
1.03.11Контрольная работа №2
Аудитория
Стр
48
51
52
№
1
2
3
Рушайло М.Ф.
Стр
229
232
234
Дома
№
1
2
3
Жукова Г.С.
(часть II)
Стр
54
54
№
4.1
4.6
Рушайло М.Ф.
Стр
235
236
№
1
6
Жукова Г.С.
(часть II)

































































































 Математика
Математика








