Похожие презентации:
Моделирование технологических процессов
1. Моделирование технологических процессов
Совокупность понятий и отношений, выраженных при помощи системыматематических символов и обозначений и отражающих некоторые свойства
изучаемого объекта, и называют математической моделью этого объекта.
1
2. Цели моделирования
модель нужна для понимания внутренней структурыисследуемого объект, процесса или явления, выявления
основных свойств, законов развития и взаимодействия с
окружающим миром
модель нужна для управления объектом, процессом или явлением,
определения оптимальных способов управления при заданных
целях и критериях
модель нужна для прогнозирования прямые и косвенные
последствия реализации заданных способов и форм воздействия на
объект, процесс или явление
2
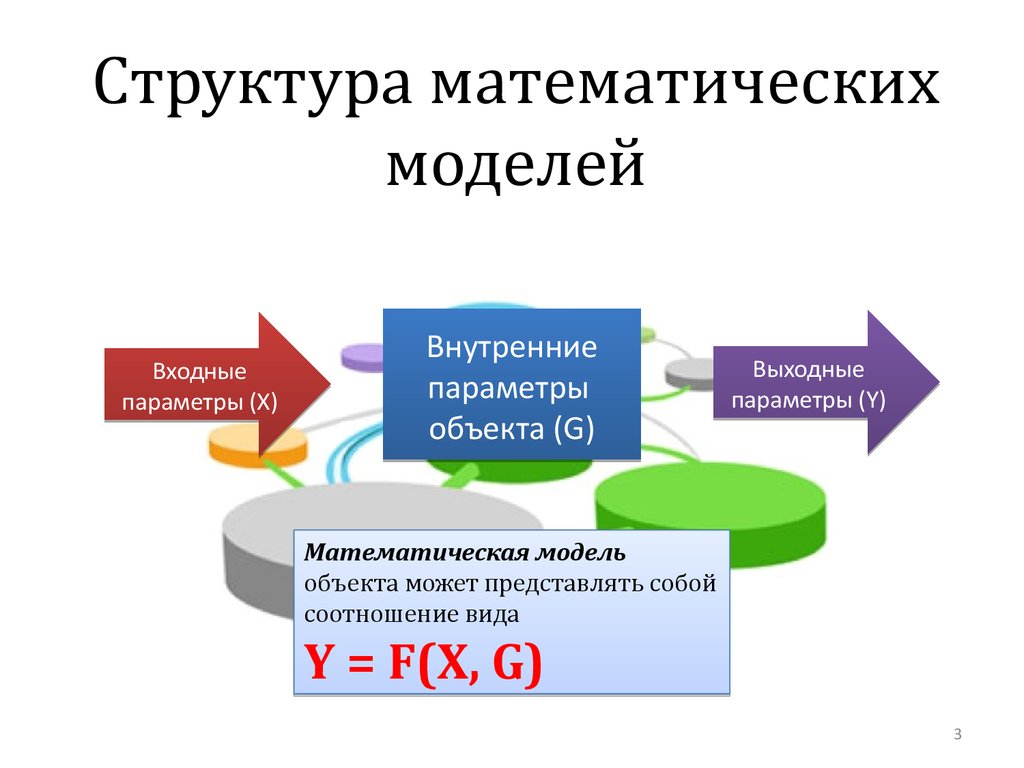
3. Структура математических моделей
Входныепараметры (X)
Внутренние
параметры
объекта (G)
Выходные
параметры (Y)
Математическая модель
объекта может представлять собой
соотношение вида
Y = F(X, G)
3
4.
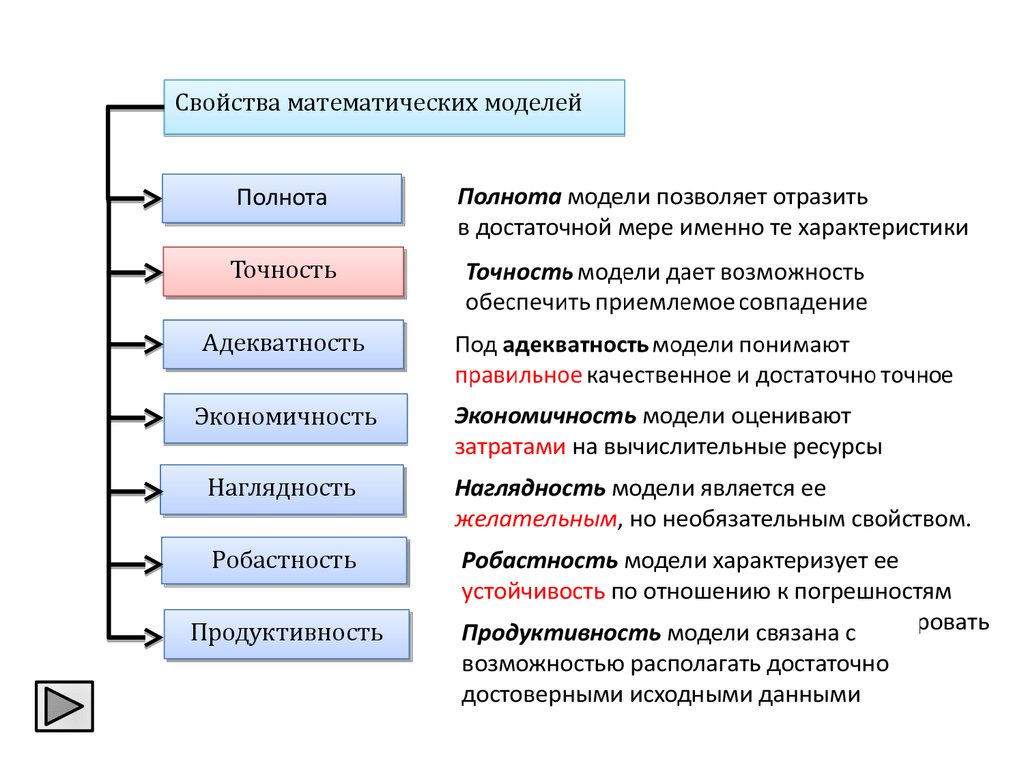
Свойства математических моделейПолнота
Полнота
Точность
Точность
Адекватность
Адекватность
Экономичность
Наглядность
Наглядность
Робастность
Робастность
Продуктивность
Продуктивность
Полнота модели позволяет отразить
в достаточной мере именно те характеристики
иТочность
особенности
объекта,
которые интересны с
модели
дает возможность
точки
зренияприемлемое совпадение
обеспечить
поставленной
цели измеренных
проведения и
экспериментально
Под
адекватность модели
понимают
вычислительного
эксперимента
найденных качественное
при помощи модели
значений
правильное
и достаточно
точное
выходных
параметров
объекта.
количественное
описание
именно тех
Экономичность
модели
оценивают
Способы
оценки
точности
модели:
характеристик
объекта,
которые
важны в
затратами
на
вычисли
тельные
ресурсы
1)
данном
конкретном
случае.
(машинное
время
и
память),
необходимые
2)
Наглядность модели
является
ее
для
реализации
модели
на
ЭВМ.
желательным, но необязательным свойством.
Робастность
модели
характеризует
ее
Эти
затраты зависят
от раз
мерности
Использование
математических
моделей и их
по отноше
нию ее
к погрешностям
–устойчивость
заданное значение
погрешности
модели
пространства
фазовых
переменных,
от
модификация
упрощаются,
если
составляющие
исходных
данных,
способность
ихинивели
(например,
отдельные
члены уравнений)
имеютровать
ясный
особенностей
применяемой
ЭВМ
Продуктивность
модели
связана
сдругих
и
не допускатьсмысл.
чрезмерного
влияния на
содержательный
факторов.
возможностью
располагать достаточно
результат
численного
эксперимента
достоверными
исходными
данными
5.
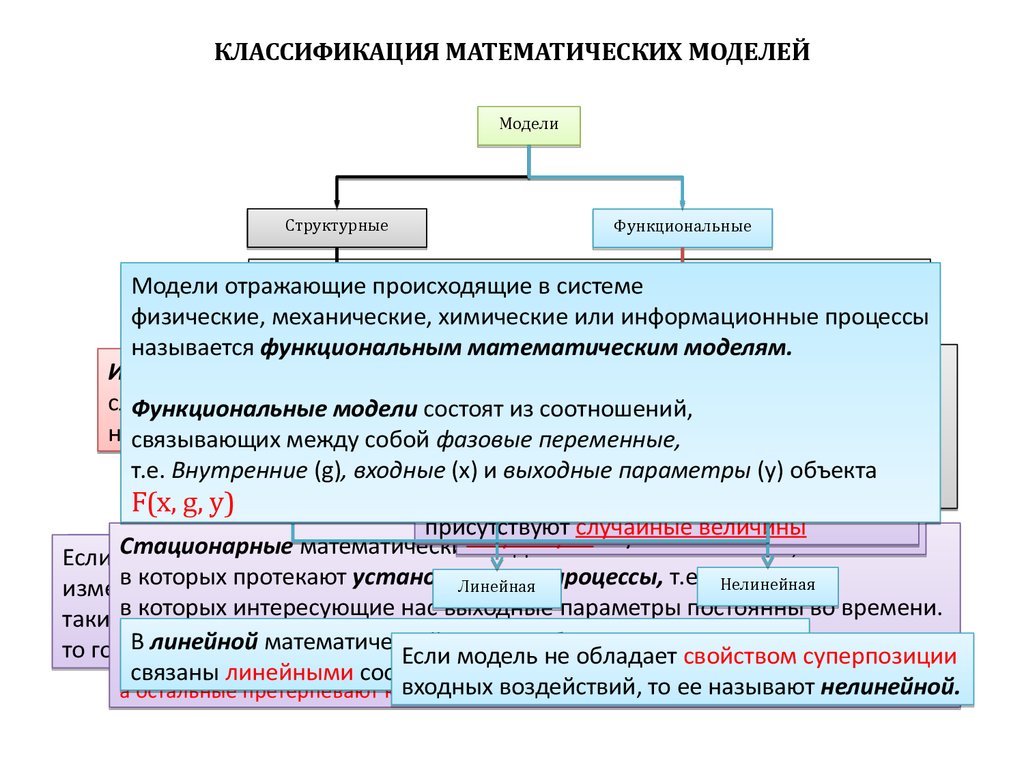
КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙМодели
Структурные
Функциональные
Если модель
отображает устройство
Модели отражающие
происходящие
в системе объекта
имеханические,
связи между
составляющими
элементами,
Аналитическая процессы
Топологические
Геометрические
Имитационная
физические,
химические
илиего
информационные
то ее называют структурной
математиче
ской моделью.
называется функциональным
математиче
ским моделям.
Топологические
модели отображают
объектаописание
Геометрическая
модельсостав
дополнительно
к информации,
Имитационной
математической
моделью
называется
Аналитическими
моделями
называются
модели,
и
связи
между
его
элементами
пред
ставленной
в
топологической
модели,
сложных
объектов при
помощи
совокупности
его реакций
Стохастические
Детерминированные
Функциональные
модели
состоят
из соотношений,
которые
имеют
аналитические
связи
содержит
опеременные,
форме
насвязываю
некоторые
известные
(илисведения
заданные)
входные воздействия (сигналы)
щих
между
собой
фазовые
между
фазовыми
переменными
модели
и размерах
объекта
и его элементах,
Модель
называют
стохастической
т.е. Внутренние (g),
входные
(x)Модель
и выходные
параметры
(y) объекта
называют детерминированной
об их взаимном
расположении
Стационарные
Квазистационарные
если
среди
ее фазовых
переменных
(x, g, y)
F(x, g, y)Динамические
если
среди
ее фазовых
переменных
присутствуют
случайные
величины
отсутствуют
случайные
величины
Стационарные
математические
модели
описывают
объекты,
Если
Динамической
интересующие
моделью
нас выходные
называется
параметры
модель,объекта
описывающая изменение
в
которых
протекают
установившиеся
процессы,
т.е. процессы,
Нелинейная
Линейная
изменя
параметров
ются медленно
моделируемого
и в рассматриваемый
объекта
с течением
фиксированный
времени
x(t),
момент
g(t), y(t)
времени
в изменением
которых
ресующие
нас выходные параметры постоянны во времени.
таким
и влияние
его инте
инерци
можно
онных
пренебречь,
свойств.
*К
процессам относят
и периодические
процессы,
В установившимся
линейной
математической
модели
объектамодели.
его параметры
то говорят
о
квазистационарной
математической
Если
модель
не
обладает
свойством суперпозиции
всвязаны
которых некоторые
выходные
параметры y остаются неизменными,
линейными
соотношениями.
входных воздействий, то ее называют нелинейной.
а остальные претерпевают колебания.
6.
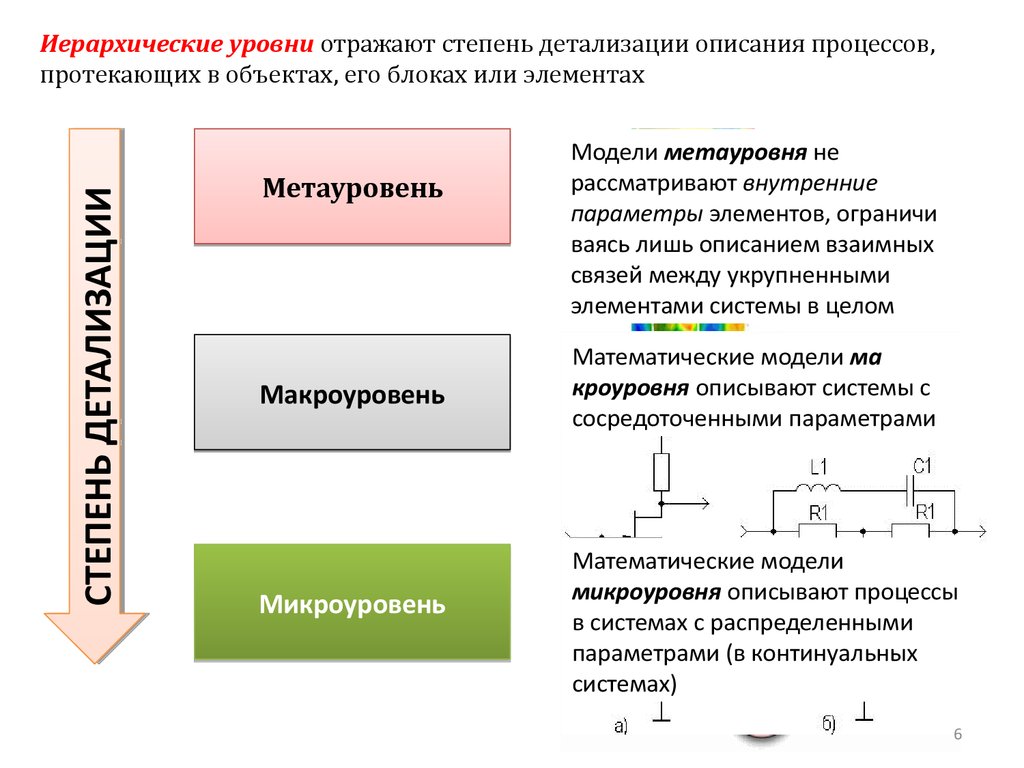
СТЕПЕНЬ ДЕТАЛИЗАЦИИИерархические уровни отражают степень детализации описания процессов,
протекающих в объектах, его блоках или элементах
Метауровень
Макроуровень
Микроуровень
Модели метауровня не
рассматривают внутренние
параметры элементов, ограничи
ваясь лишь описанием взаимных
связей между укрупненными
элементами системы в целом
Математические модели ма
кроуровня описывают системы с
сосредоточенными параметрами
Математические модели
микроуровня описывают процессы
в системах с распределенными
параметрами (в континуальных
системах)
6
7. Математические модели макроуровня
МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАКРОУРОВНЯфазовые переменные зависят только от времени
Входные и Выходные параметры
Связь между этими величинами
устанавливают при помощи уравнений
состояния элемента, в которые входят
также и его внутренние параметры
Потенциальные величины
Потоковые величины
7
8.
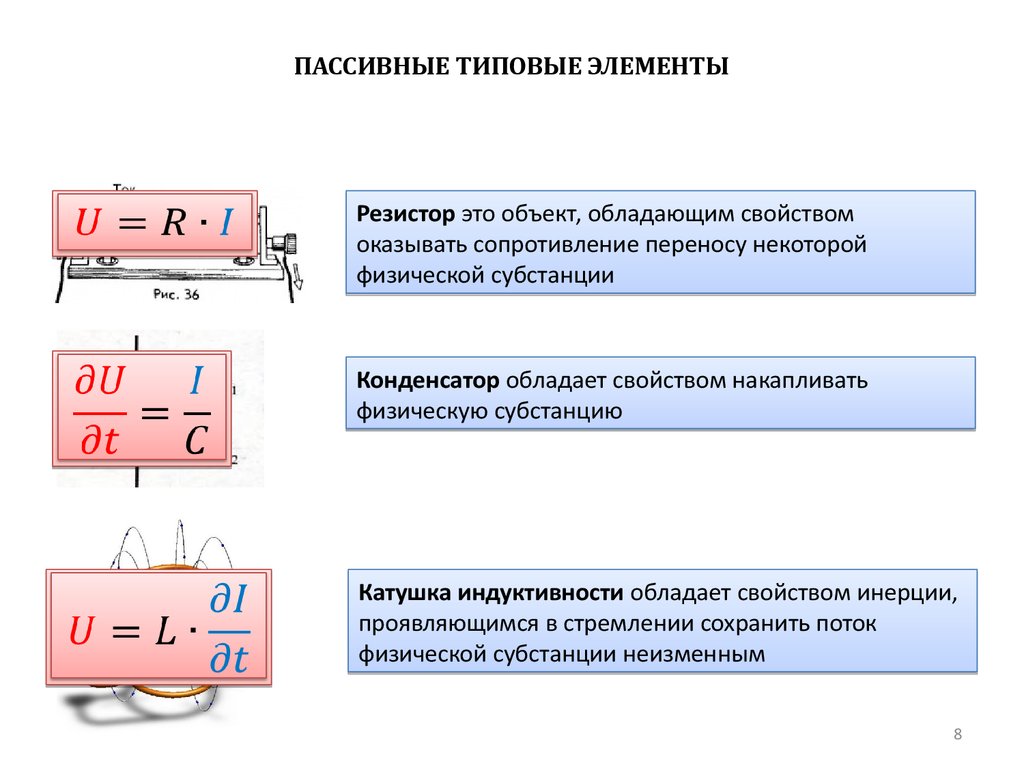
ПАССИВНЫЕ ТИПОВЫЕ ЭЛЕМЕНТЫРезистор это объект, обладающим свойством
оказывать сопротивление переносу некоторой
физической субстанции
Конденсатор обладает свойством накапливать
физическую субстанцию
Катушка индуктивности обладает свойством инерции,
проявляющимся в стремлении сохранить поток
физической субстанции неизменным
8
9.
АКТИВНЫЕ ТИПОВЫЕ ЭЛЕМЕНТЫИдеальный источник потенциальной величины
является объект или устройство, у которого выходная
потенциальная величина не зависит от его входной
потоковой величины
Идеальный источник потоковой величины является
объект или устройство, у которого выходная потоковая
величина не зависит от его входной потенциальной
величины
9
10. Механические системы
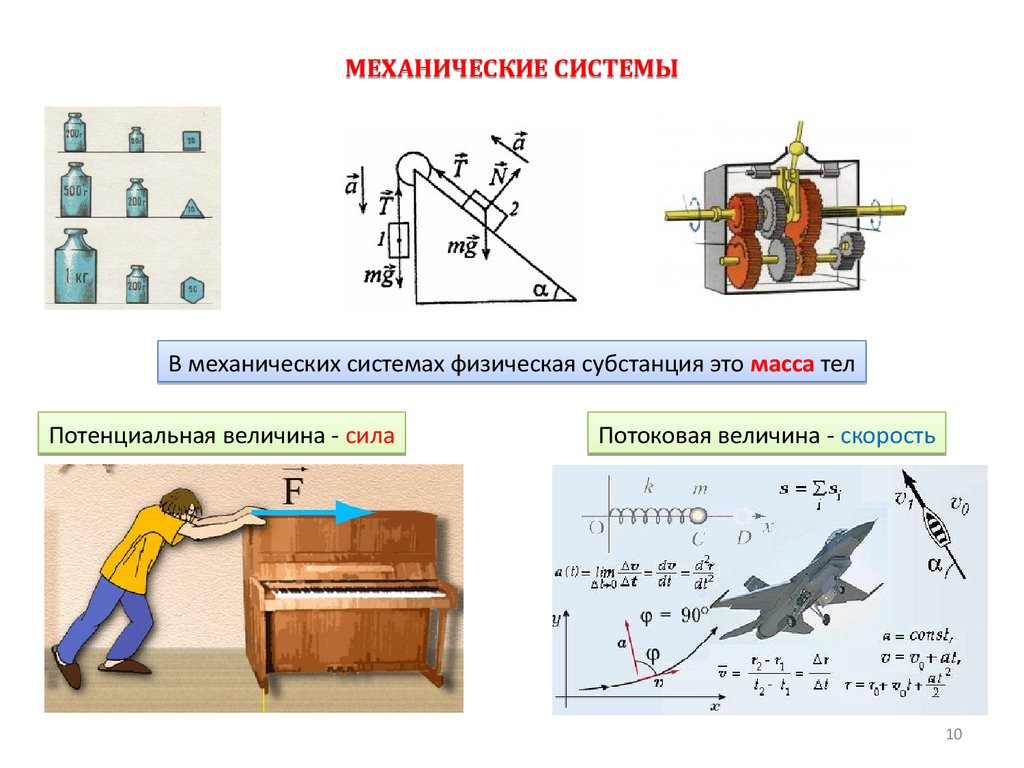
МЕХАНИЧЕСКИЕ СИСТЕМЫВ механических системах физическая субстанция это масса тел
Потенциальная величина - сила
Потоковая величина - скорость
10
11. Механическое сопротивление
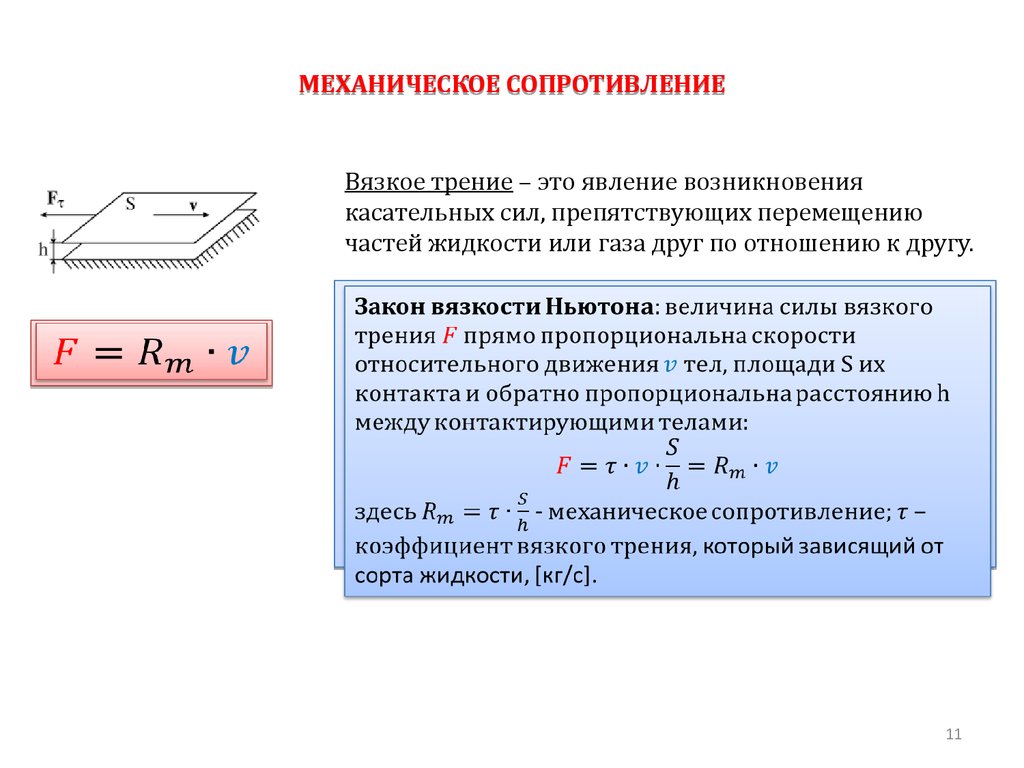
МЕХАНИЧЕСКОЕ СОПРОТИВЛЕНИЕВязкое трение – это явление возникновения
касательных сил, препятствующих перемещению
частей жидкости или газа друг по отношению к другу.
Закон вязкости Ньютона: величина силы вязкого
трения прямо пропорциональна скорости
относительного движения тел, площади S их
контакта и обратно пропорциональна расстоянию h
между контактирующими телами:
здесь - механическое сопротивление; – коэффициент
вязкого трения, который зависящий от сорта жидкости,
[кг/с].
11
12. механическая емкость
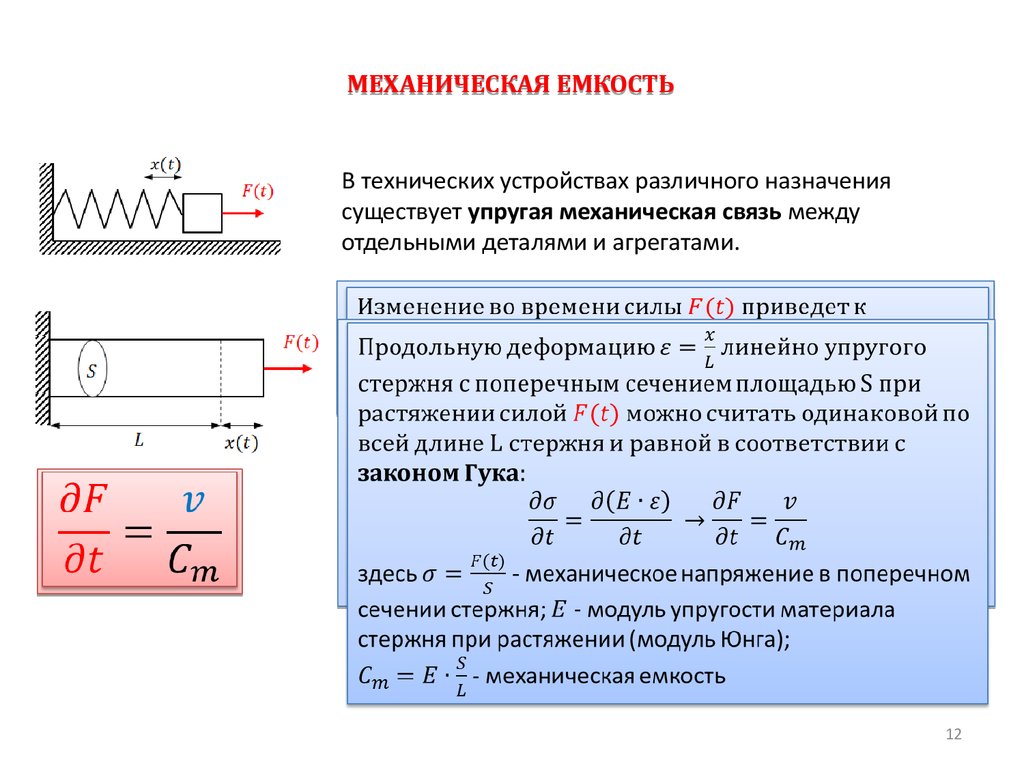
МЕХАНИЧЕСКАЯ ЕМКОСТЬВ технических устройствах различного назначения
существует упругая механическая связь между
отдельными деталями и агрегатами.
Изменение во времени силы приведет к изменению
пе
ремещениядеформацию
груза :
Продольную
линейно упругого стержня
с поперечным сечением площадью S при растяжении
здесь
механическая
емкость;
- жесткость
пружины.
силой - можно
считать
одинаковой
по всей
длине L
стержня и равной в соответствии с законом Гука:
здесь - механическое напряжение в поперечном сечении
стержня; - модуль упругости материала стержня при
растяжении (модуль Юнга);
- механическая емкость
12
13. Механическая индуктивность
МЕХАНИЧЕСКАЯ ИНДУКТИВНОСТЬВ механических системах все отдельные звенья и агрегаты
обладают определенной массой.
2-й закон Ньютона: в случае поступательного движения
ускорение, приобретаемое телом, прямо
пропорционально вызывающей его силе, совпадает с ней
по направлению и обратно пропорционально массе тела.
здесь - механическая индуктивность.
13
14. Тепловые системы
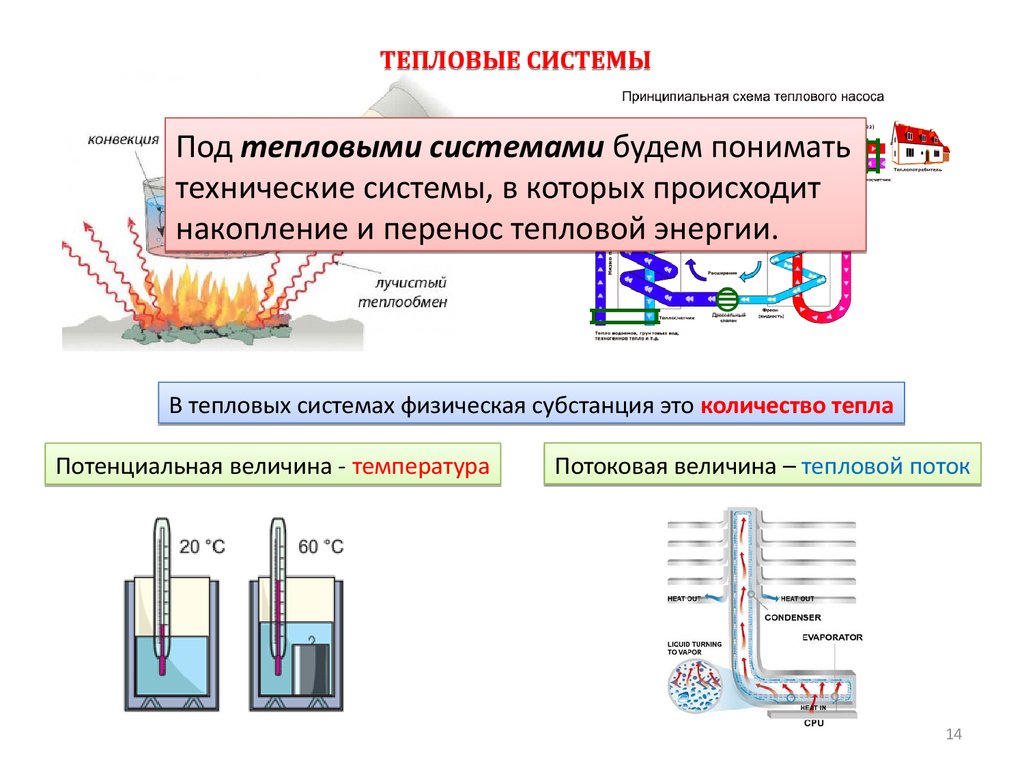
ТЕПЛОВЫЕ СИСТЕМЫПод тепловыми системами будем понимать
технические системы, в которых происходит
накопление и перенос тепловой энергии.
В тепловых системах физическая субстанция это количество тепла
Потенциальная величина - температура
Потоковая величина – тепловой поток
14
15. Тепловое сопротивление
ТЕПЛОВОЕ СОПРОТИВЛЕНИЕМногие элементы конструкции тепловых
систем могут быть сведены к расчетной схеме
плоской стенки толщиной
В соответствии с эмпирическим законом
теплопроводности Фурье, тепловой поток ,
проходящий через стенку, одна из
поверхностей которой имеет площадь S,
пропорционален разности температур :
- коэффициент теплопроводности;
- разность температур на стенках пластины;
- термическое сопротивление пластины.
15
16. Тепловая емкость
ТЕПЛОВАЯ ЕМКОСТЬЕсли некоторая деталь или конструкция
выполнены из материала с высокой
теплопроводностью, то их температуру
можно приближенно постоянной во всем
объеме конструкции V.
В этом случае тепловое состояние
конструкции в любой текущий момент
времени t допустимо характеризовать
лишь одним значением температуры .
При изменении температуры во времени тепловая
энергия тела постоянной конфигурации изменяется со
скоростью:
здесь - полная теплоемкостью тела
16
17. Тепловая индуктивность
ТЕПЛОВАЯ ИНДУКТИВНОСТЬЭмпирический закон теплопроводности
Фурье предполагает, что в ответ на
появление в материале с конечным коэф
фициентом теплопроводности градиента
температуры мгновенно возникает
тепловой поток. Это равносильно
предположению, что скорость распростране
ния тепловой энергии в материале
бесконечно велика. Однако, в реальном
материале неизбежно некоторое
запаздывание возникновения теплового
потока по отношению к появлению
градиента температуры. Величина такого
запаздывания зависит от микромеханизма
передачи тепловой энергии в материале и
связана со временем обмена энергией между
отдельными элементами микроструктуры
материала.
17
18. Гидравлические системы
ГИДРАВЛИЧЕСКИЕ СИСТЕМЫСистемы, в которых происходит
перемещение несжимаемой жидкости,
называются гидравлическими системами
Физическая субстанция - несжимаемая жидкость
Потенциальная величина - давление
Потоковая величина – объемный расход
18
19. Ламинарное течение жидкости
ЛАМИНАРНОЕ ТЕЧЕНИЕ ЖИДКОСТИ19
20. Гидравлическое сопротивление
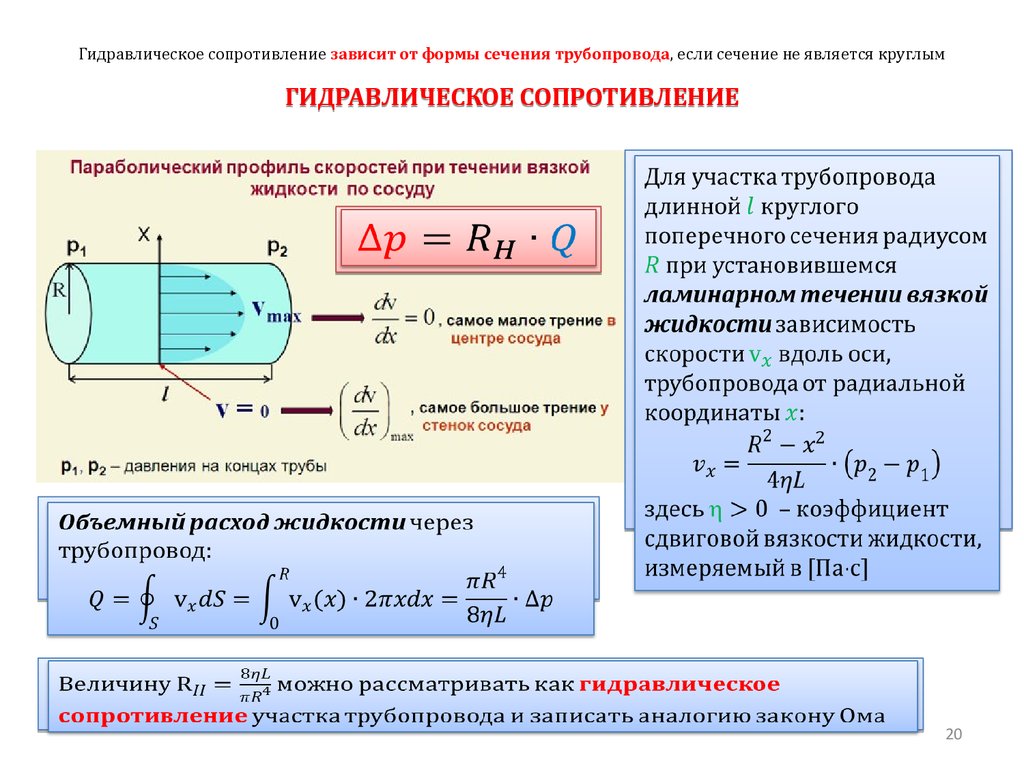
зависит от формы сечения трубопровода, если сечение не является круглымГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ
Для участка трубопровода
длинной круглого поперечного
сечения радиусом при
установившемся ламинарном
течении вязкой жидкости
зависимость скорости вдоль оси,
трубопровода от радиальной
координаты :
Объемный расход жидкости через
трубопровод:
здесь – коэффициент сдвиговой
вязкости жидкости, измеряемый
в [Па с]
Величину можно рассматривать как гидравлическое сопротивление участка
трубопровода и записать аналогию закону Ома
20
21.
При увеличении объемного расхода жидкости через трубопровод растет еескорость и ламинарный режим течения переходит в турбулентный, при
этом гидравлическое сопротивление зависит от объемного расхода жидкости,
т.е. математическая модель установившегося течения в трубопроводе
оказывается нелинейной.
21
22. Гидравлическая емкость
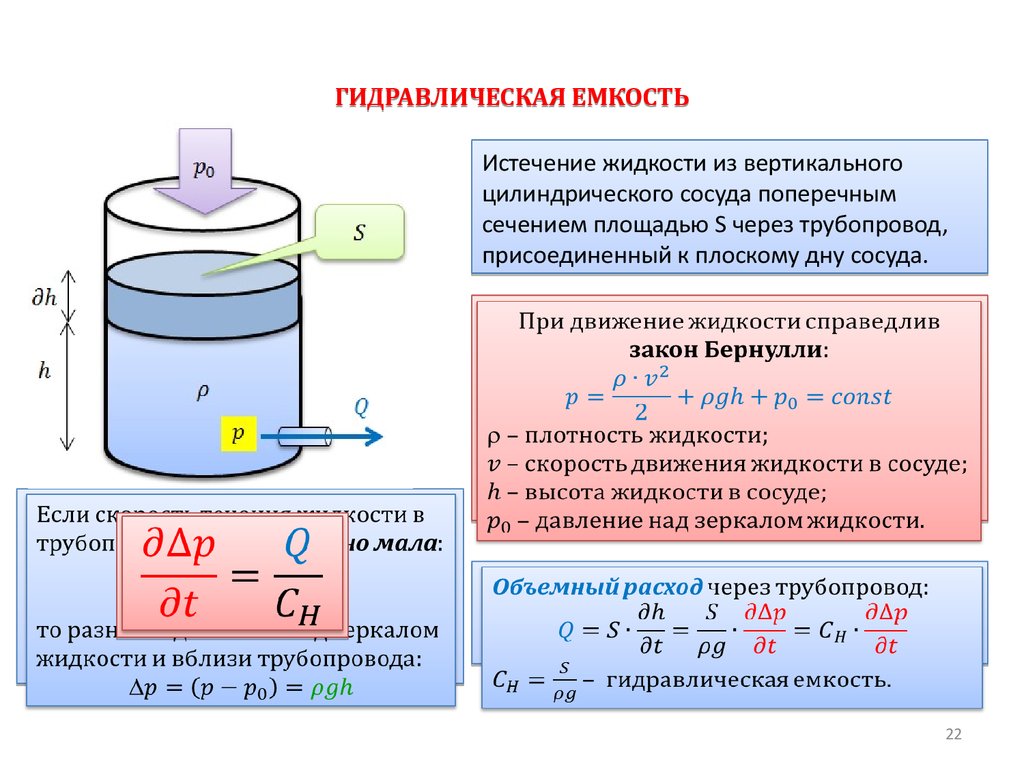
ГИДРАВЛИЧЕСКАЯ ЕМКОСТЬИстечение жидкости из вертикального
цилиндрического сосуда поперечным
сечением площадью S через трубопровод,
присоединенный к плоскому дну сосуда.
При движение жидкости справедлив закон
Бернулли:
Если скорость течения жидкости в
трубопроводе достаточно мала:
то разность давлений над зеркалом
жидкости и вблизи трубопровода:
– плотность жидкости;
– скорость движения жидкости в сосуде;
– высота жидкости в сосуде;
– давление над зеркалом жидкости.
Объемный расход через трубопровод:
– гидравлическая емкость.
22
23. Гидравлическая индуктивность
ГИДРАВЛИЧЕСКАЯ ИНДУКТИВНОСТЬРассмотрим участок горизонтального
цилиндрического трубопровода длиной L
и площадью поперечного сечения S, по
которому течет с переменным во времени
объемным расходом идеальная
(невязкая) несжимаемая жидкость
плотностью .
При переменном расходе за счет
ускорения массы жидкости возникнет
сила инерции:
В некоторый момент времени t на участке
трубопровода находится
или
или жидкость
массой , которая движется со скоростью:
здесь
здесь --гидравлическая
гидравлическаяиндуктивность
индуктивность
участка
–участка
объемтрубопровода
жидкости.
трубопроводааналогичная
аналогичная
индуктивности
индуктивностикатушки
катушки
Так как жидкость идеальная, то гидравлическое сопротивление при ее течении
отсутствует , и сила инерции уравновешена лишь разностью сил давления в
поперечных сечениях трубопровода
23
24. Аналогия элементов моделей макроуровня
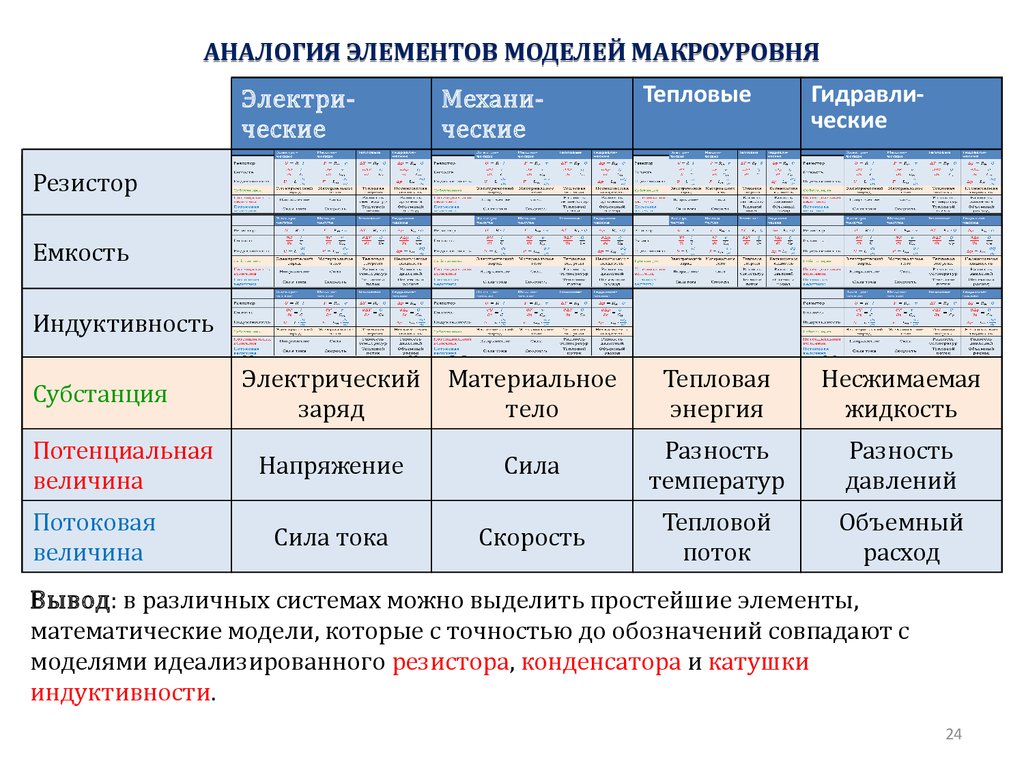
АНАЛОГИЯ ЭЛЕМЕНТОВ МОДЕЛЕЙ МАКРОУРОВНЯЭлектрические
Механические
Тепловые
Субстанция
Субстанция
Электрический
Электрический
заряд
заряд
Материальное
Материальное
тело
тело
Потоковая
величина
Сила тока
Скорость
Тепловая
Тепловая
энергия
энергия
Разность
Разность
температур
температур
Резистор
Резистор
Гидравлические
Емкость
Индуктивность
Индуктивность
Потенциальная
Потенциальная
величина
величина
Напряжение
Напряжение
Сила
Сила
Тепловой
поток
Несжимаемая
Несжимаемая
жидкость
жидкость
Разность
Разность
давлений
давлений
Объемный
расход
Вывод: в различных системах можно выделить простейшие элементы,
математические модели, которые с точностью до обозначений совпадают с
моделями идеализированного резистора, конденсатора и катушки
индуктивности.
24
25. Адекватность моделей макроуровня
АДЕКВАТНОСТЬ МОДЕЛЕЙ МАКРОУРОВНЯПрименение математических моделей макроуровня
простейших типовых элементов для описания
реальных систем вызывает неизбежные погрешности.
Одной из причин возникновения погрешностей при исполь
зовании математической модели макроуровня является
пренебрежение простран ственным распределением
параметров, характеризующих свойства типовых элементов и
протекающие в них процессы
Поэтому для выявления области адекватности
моделей макроуровня даже простых элементов
(резистор, конденсатор или катушка индуктивности)
требуется рассмотрение математических моделей
микроуровня физических процессов протекающих в
этих объектах
25
26. Математические модели систем типовых элементов
МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИСТЕМ ТИПОВЫХ ЭЛЕМЕНТОВПри математическом моделировании технического устройства, в котором
протекают процессы различной физической природы, прежде всего
необходимо для каждого из таких процессов выделить типовые элементы,
образующие однородную по физическим свойствам электрическую,
механическую, тепловую, гидравлическую и т.п. систему.
Электрическая
подсистема
Гидравлическая
подсистема
Механическая
подсистема
Тепловая
подсистема
26
27.
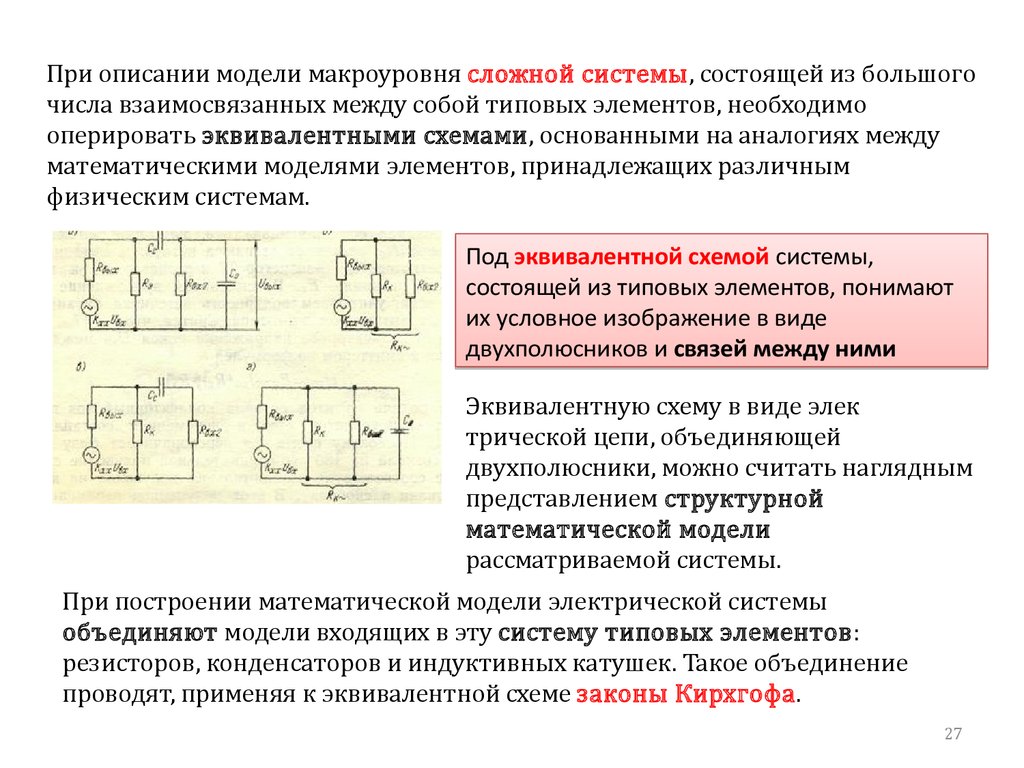
При описании модели макроуровня сложной системы, состоящей из большогочисла взаимосвязанных между собой типовых элементов, необходимо
оперировать эквивалентными схемами, основанными на аналогиях между
математическими моделями элементов, принадлежащих различным
физическим системам.
Под эквивалентной схемой системы,
состоящей из типовых элементов, понимают
их условное изображение в виде
двухполюсников и связей между ними
Эквивалентную схему в виде элек
трической цепи, объединяющей
двухполюсники, можно считать наглядным
представлением структурной
математической модели
рассматриваемой системы.
При построении математической модели электрической системы
объединяют модели входящих в эту систему типовых элементов:
резисторов, конденсаторов и индуктивных катушек. Такое объединение
проводят, применяя к эквивалентной схеме законы Кирхго фа.
27
28. Законы Кирхгофа
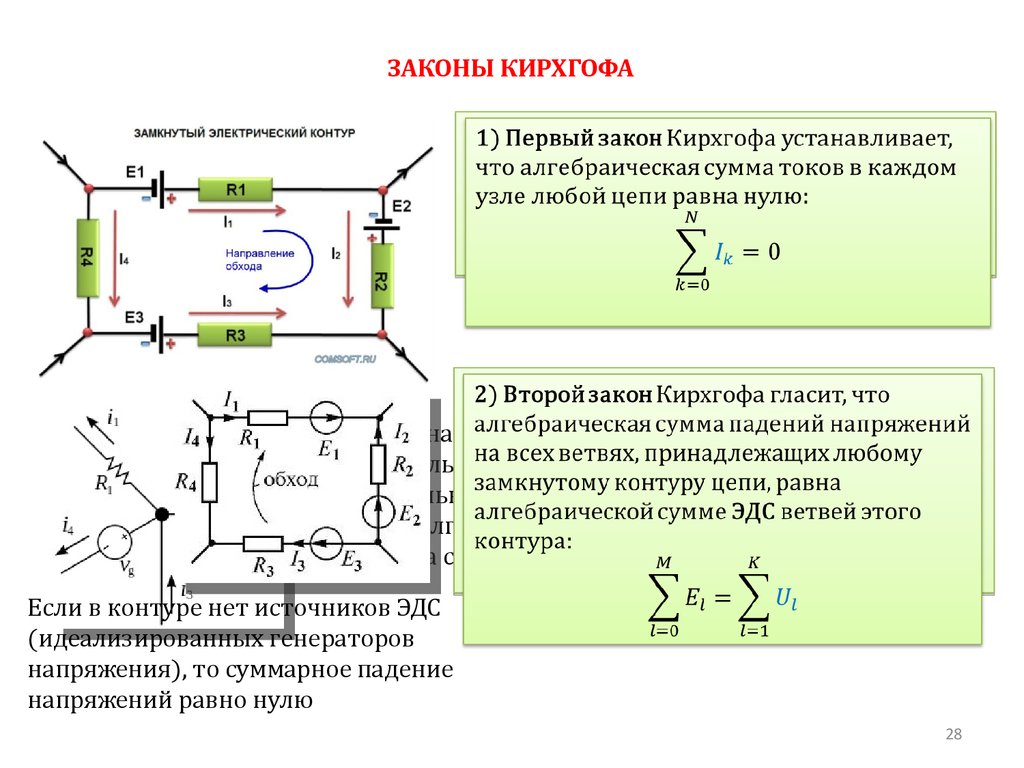
ЗАКОНЫ КИРХГОФА1) Первый закон Кирхгофа устанавливает,
что алгебраическая сумма токов в каждом
узле любой цепи равна нулю:
2) Второй закон Кирхгофа гласит, что
алгебраическая
сумма
падений считать
напряжений
При этом направленный
к узлу
ток принято
на всех
ветвях, принадлежащих
положительным,
а направленный
от узла – любому
замкнутому контуру цепи, равна
отрицательным.
алгебраической
сумме
ЭДС
ветвей этого к
Поэтому алгебраическая
сумма
токов,
направленных
контура:
узлу равна сумме
направленных от узла.
Если в контуре нет источников ЭДС
(идеализированных генераторов
напряжения), то суммарное падение
напряжений равно нулю
28
29. Механические системы
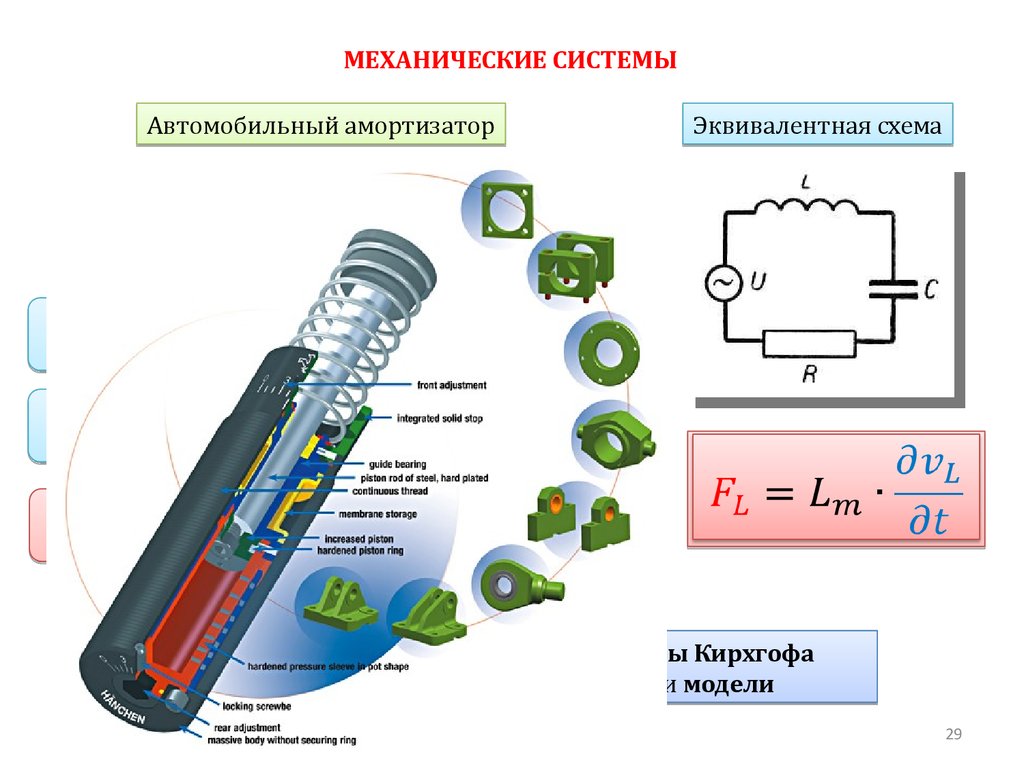
МЕХАНИЧЕСКИЕ СИСТЕМЫАвтомобильный амортизатор
конденсатор
индуктивность
Эквивалентная схема
Типовые
элементы
сопротивление
Источник
напряжения
Используем законы Кирхгофа
для формулировки модели
29
30. Используем законы кирхгофа для формулировки модели
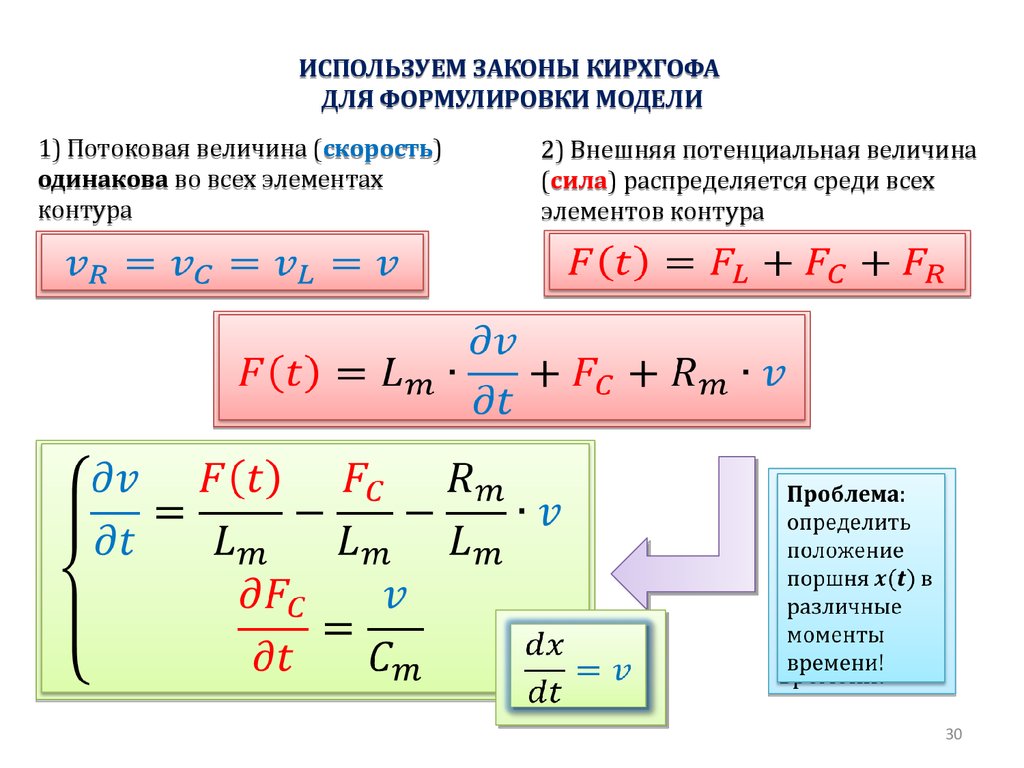
ИСПОЛЬЗУЕМ ЗАКОНЫ КИРХГОФАДЛЯ ФОРМУЛИРОВКИ МОДЕЛИ
1) Потоковая величина (скорость)
одинакова во всех элементах
контура
2) Внешняя потенциальная величина
(сила) распределяется среди всех
элементов контура
Проблема:
определить
положение
поршня в
различные
моменты
времени!
30
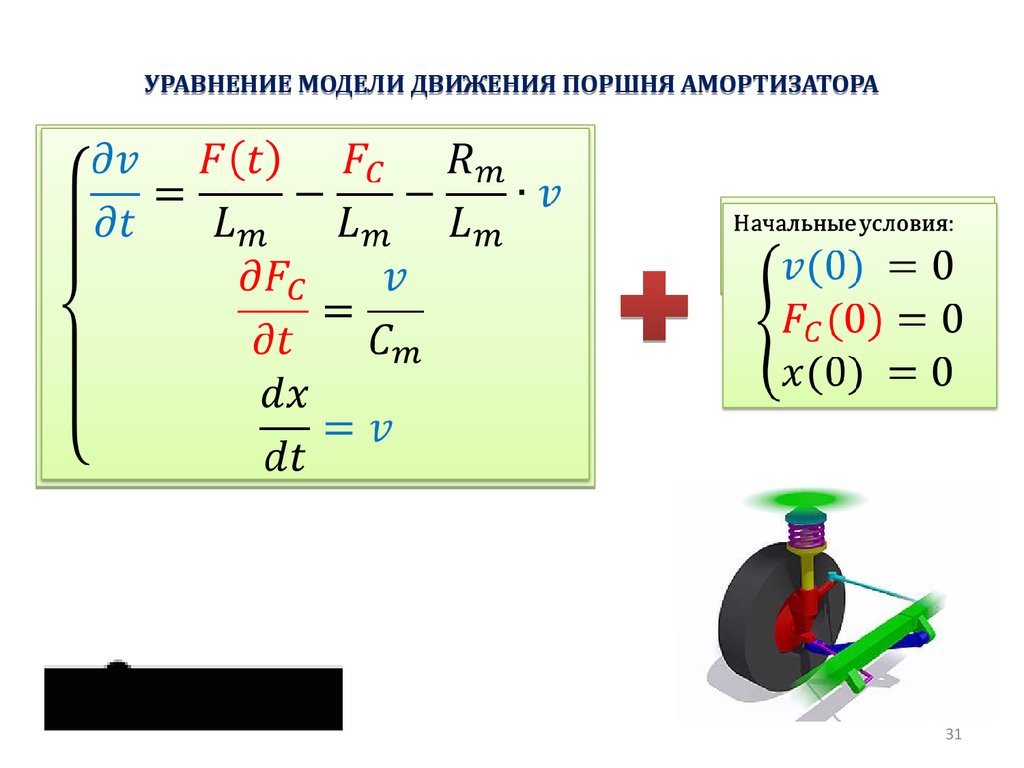
31. Уравнение модели движения поршня амортизатора
УРАВНЕНИЕ МОДЕЛИ ДВИЖЕНИЯ ПОРШНЯ АМОРТИЗАТОРАНачальные условия:
31
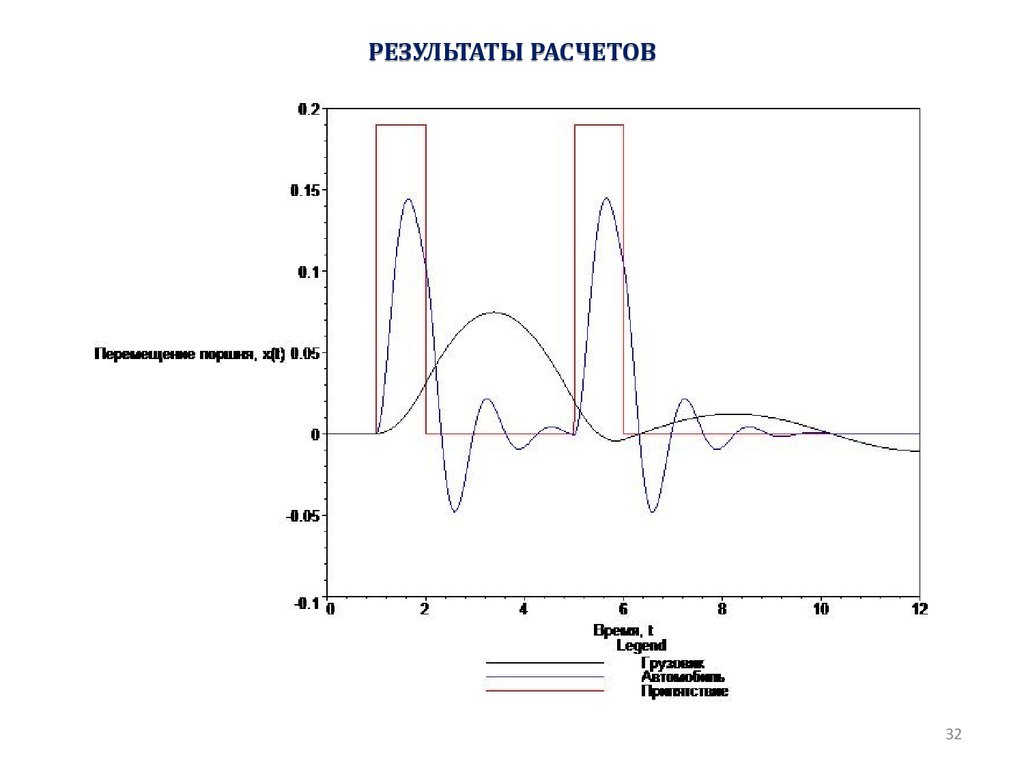
32. Результаты расчетов
РЕЗУЛЬТАТЫ РАСЧЕТОВ32
33. Нелинейные математические модели макроуровня
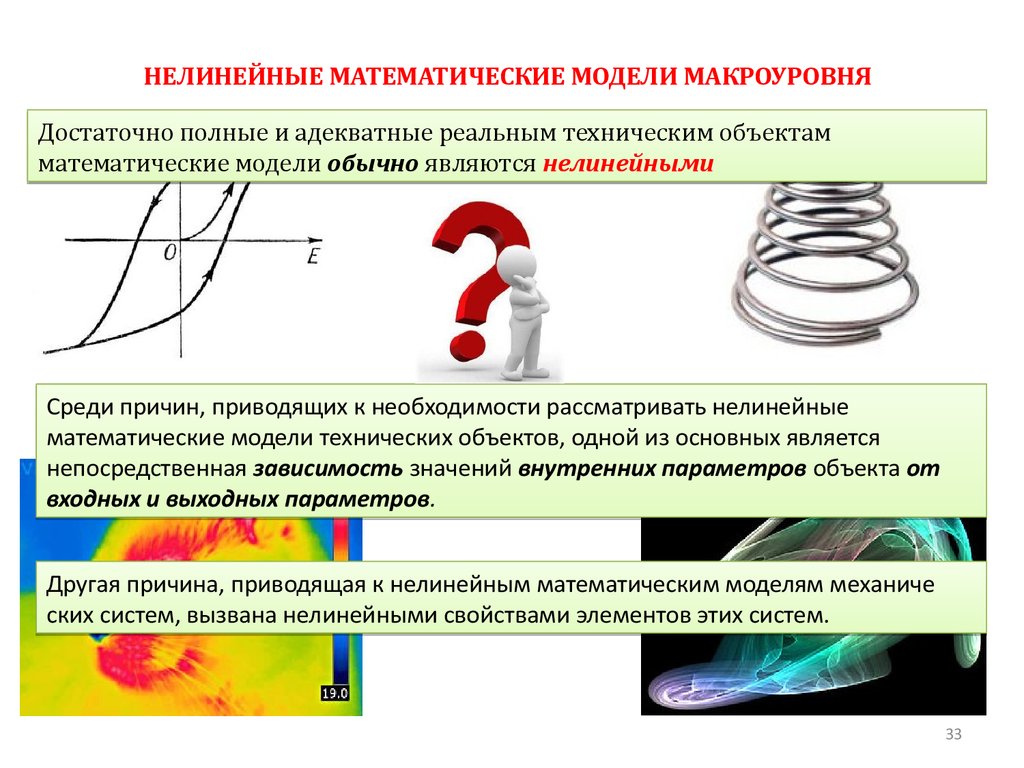
НЕЛИНЕЙНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ МАКРОУРОВНЯДостаточно полные и адекватные реальным техническим объектам
математические модели обычно являются нелинейными
Среди причин, приводящих к необходимости рассматривать нелинейные
математические модели технических объектов, одной из основных является
непосредственная зависимость значений внутренних параметров объекта от
входных и выходных параметров.
Другая причина, приводящая к нелинейным математическим моделям механиче
ских систем, вызвана нелинейными свойствами элементов этих систем.
33














 Математика
Математика Физика
Физика








