Теория Волн Ральфа Эллиота

1.

ТЕОРИЯ ВОЛН
РАЛЬФА ЭЛЛИОТА

2.

3.

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
МОДЕЛЬ
СООТНОШЕНИЕ
ВРЕМЯ

4.

ХАРАКТЕРИСТИКИ И СХЕМА ВОЛН
ЭЛЛИОТТА
МОДЕЛЬ
ИМПУЛЬС
КОРРЕКЦИЯ

5.

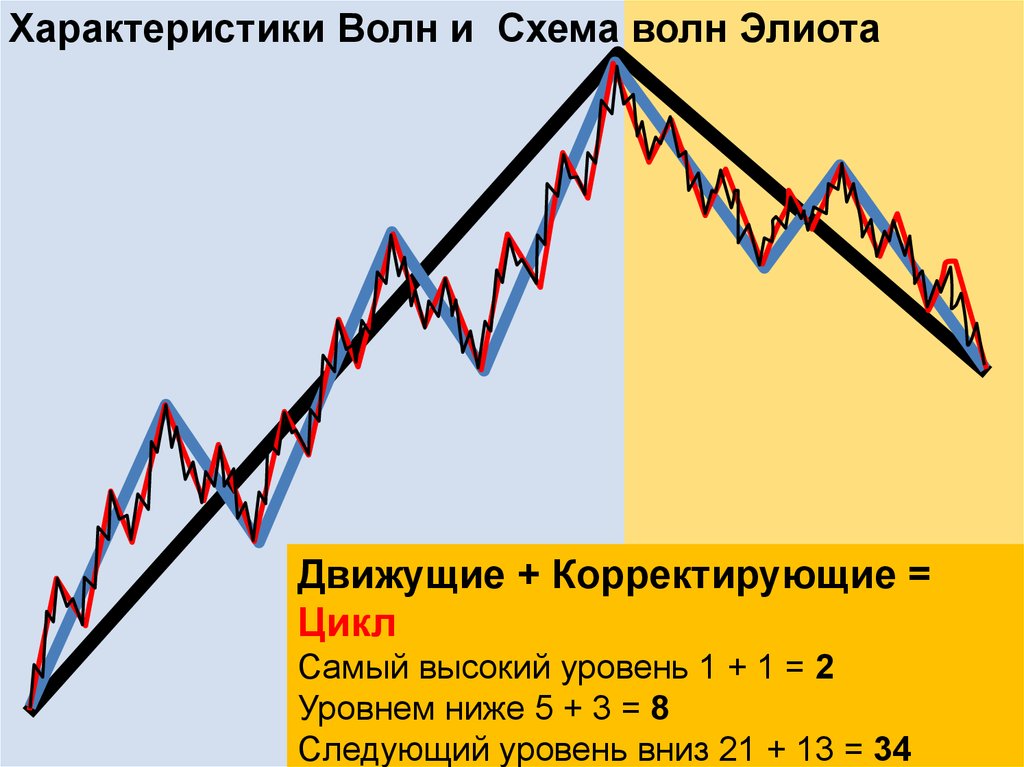
Характеристики Волн и Схема волн Элиота
Движущие + Корректирующие =
Цикл
Самый высокий уровень 1 + 1 = 2
Уровнем ниже 5 + 3 = 8
Следующий уровень вниз 21 + 13 = 34

6.

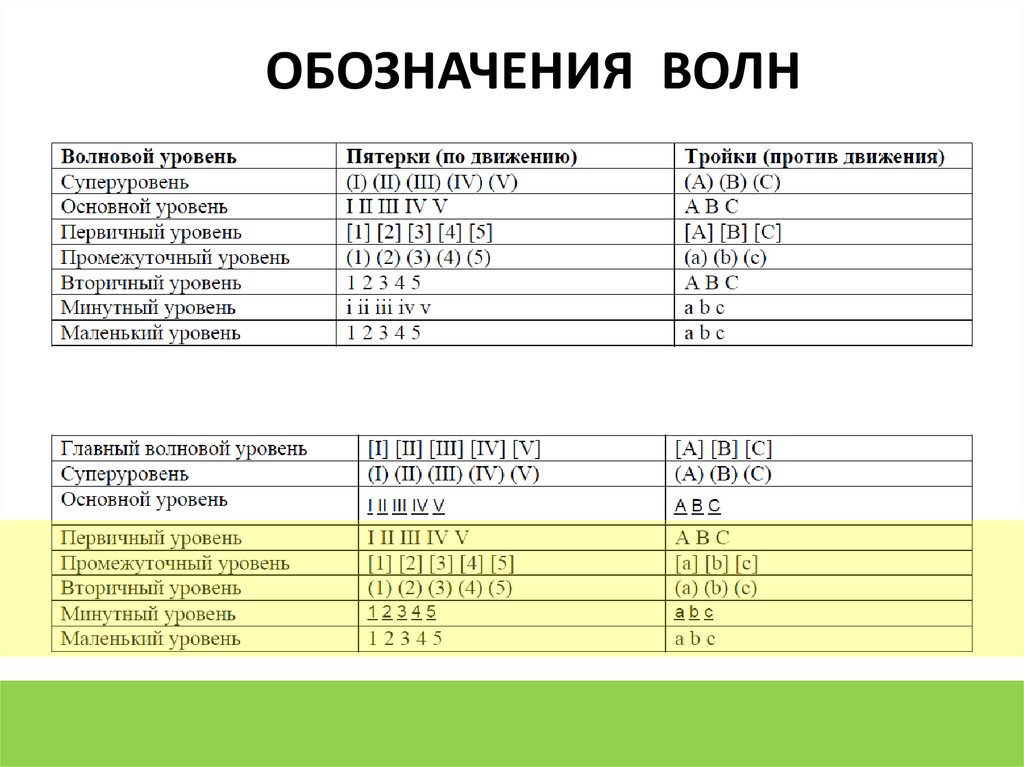
ОБОЗНАЧЕНИЯ ВОЛН

7.

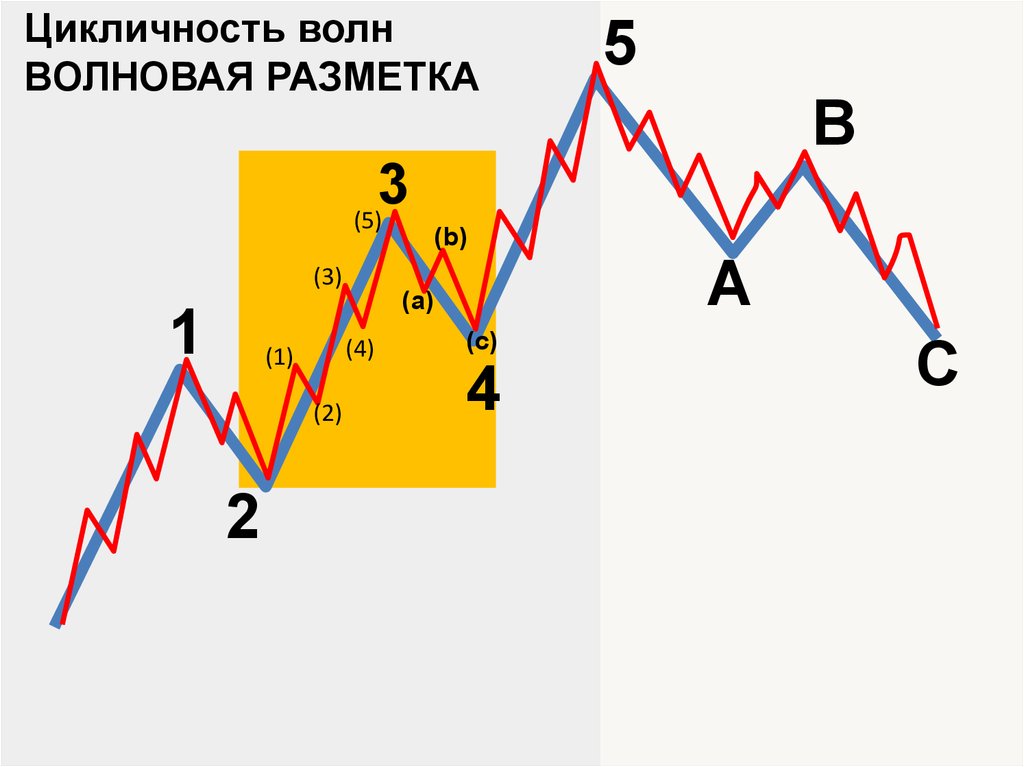
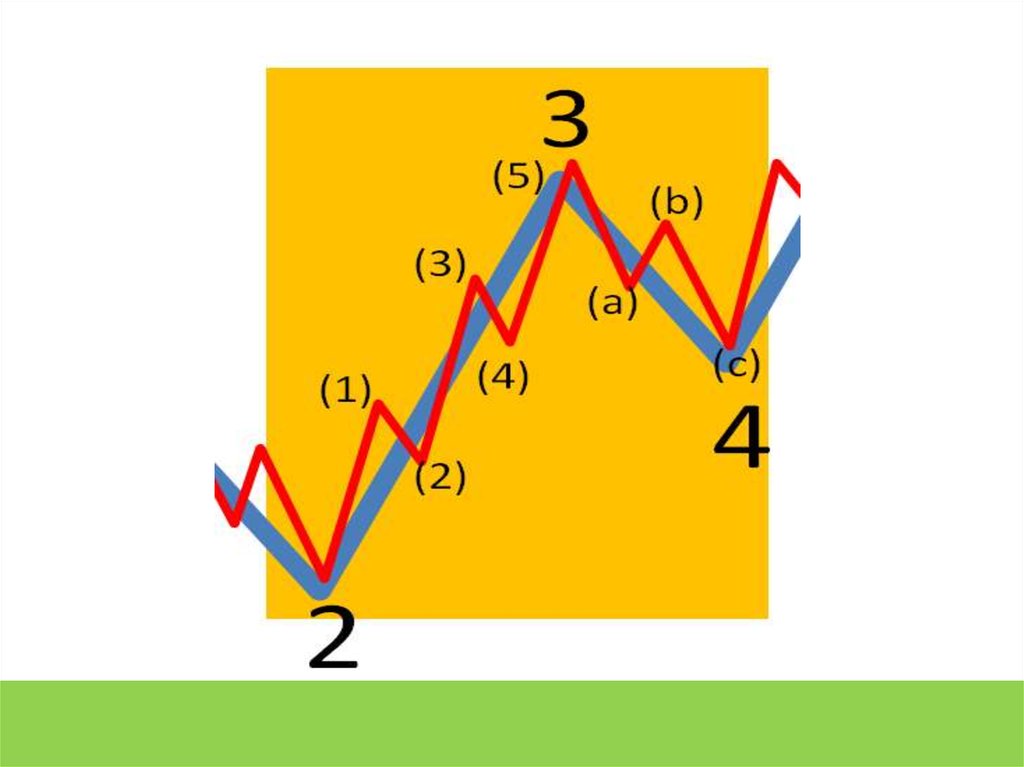
Цикличность волн
ВОЛНОВАЯ РАЗМЕТКА
5
B
3
(5)
(b)
(3)
(a)
1
(4)
(1)
(2)
2
(c)
4
А
C

8.

9.

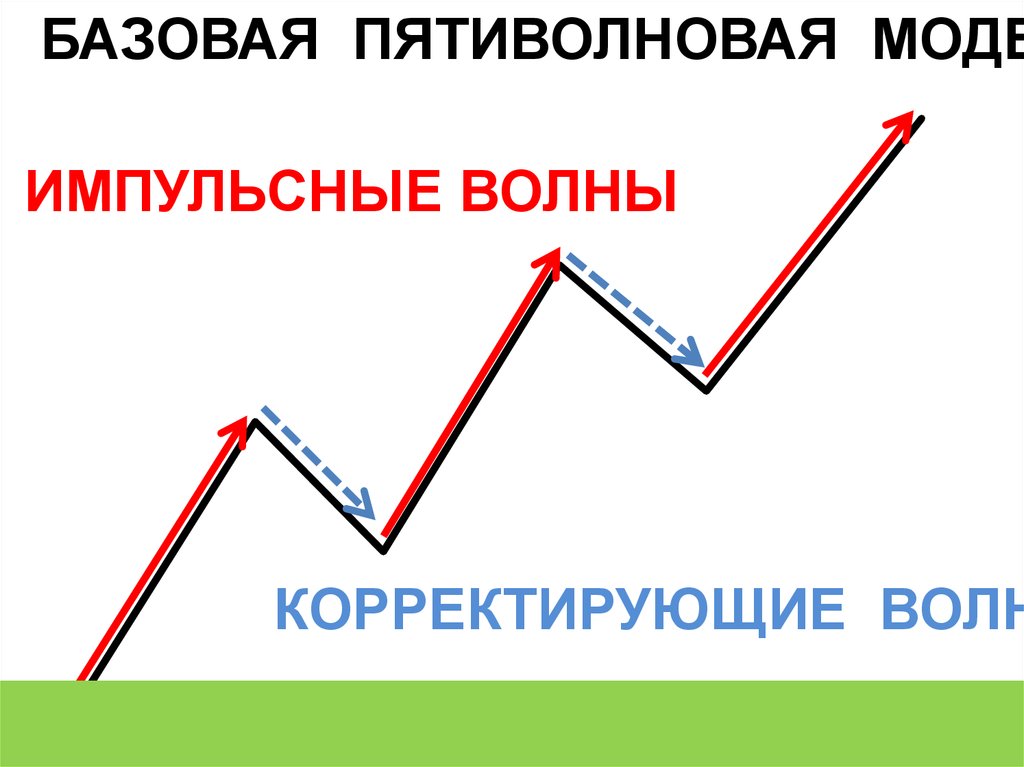
БАЗОВАЯ ПЯТИВОЛНОВАЯ МОДЕ
ИМПУЛЬСНЫЕ ВОЛНЫ
КОРРЕКТИРУЮЩИЕ ВОЛН

10.

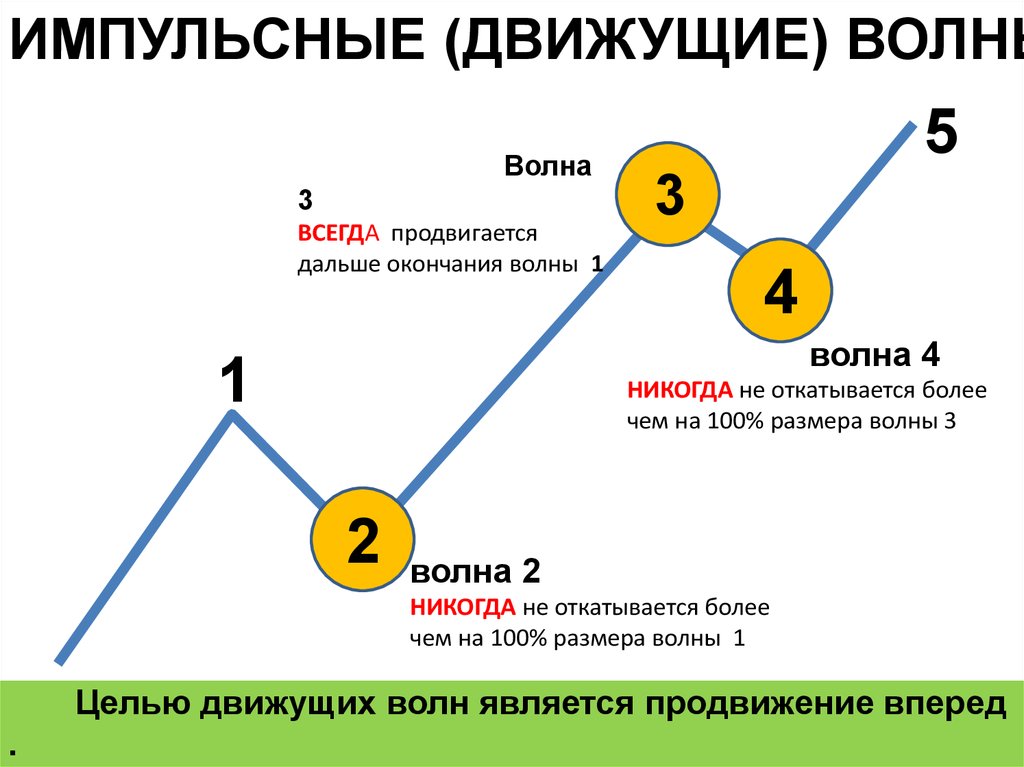
ИМПУЛЬСНЫЕ (ДВИЖУЩИЕ) ВОЛНЫ
Волна
3
ВСЕГДА продвигается
дальше окончания волны 1
5
3
4
волна 4
1
НИКОГДА не откатывается более
чем на 100% размера волны 3
2
волна 2
НИКОГДА не откатывается более
чем на 100% размера волны 1
Целью движущих волн является продвижение вперед
.

11.

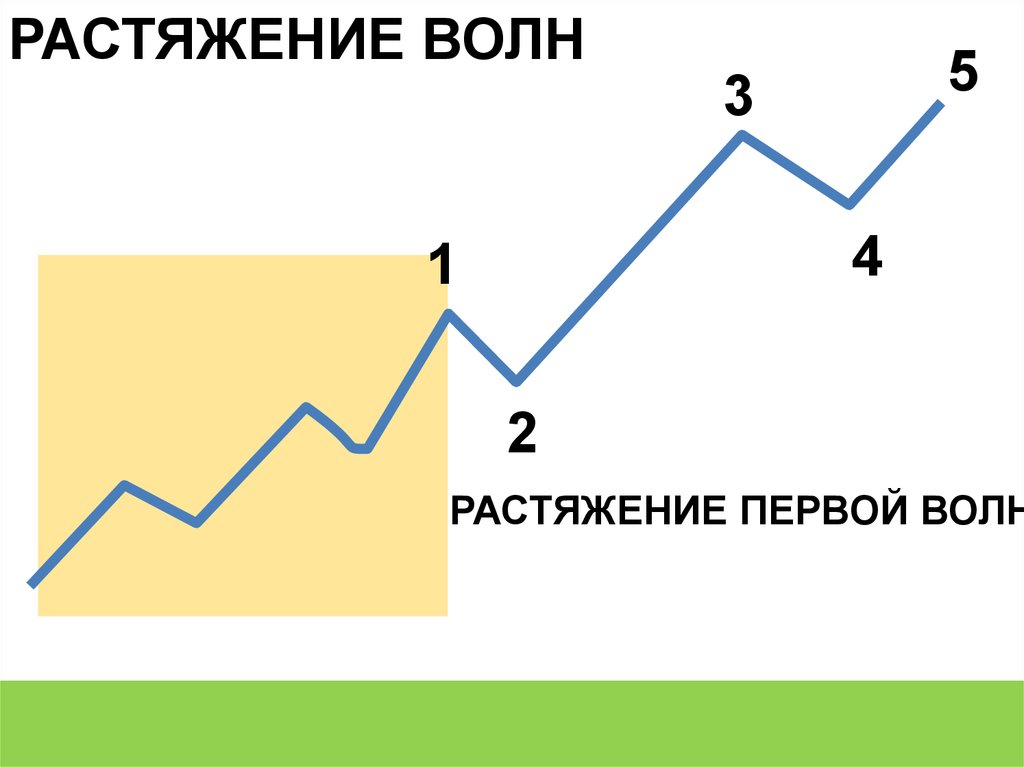
РАСТЯЖЕНИЕ ВОЛН
5
3
4
1
2
РАСТЯЖЕНИЕ ПЕРВОЙ ВОЛН

12.

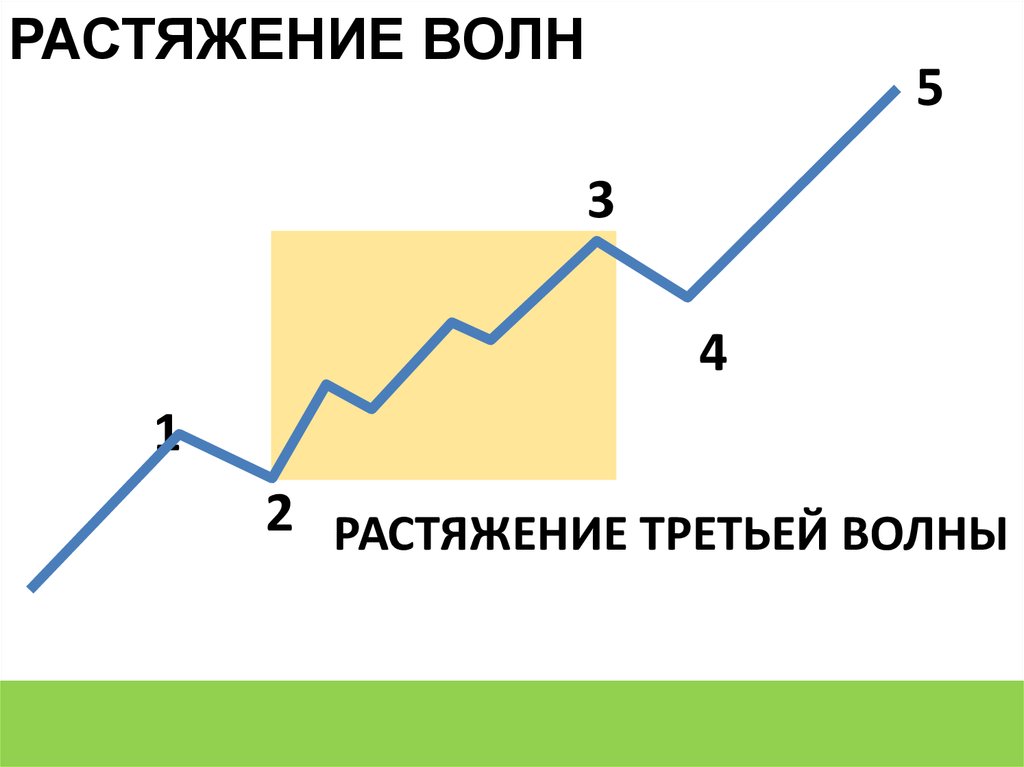
РАСТЯЖЕНИЕ ВОЛН
5
3
4
1
2 РАСТЯЖЕНИЕ ТРЕТЬЕЙ ВОЛНЫ

13.

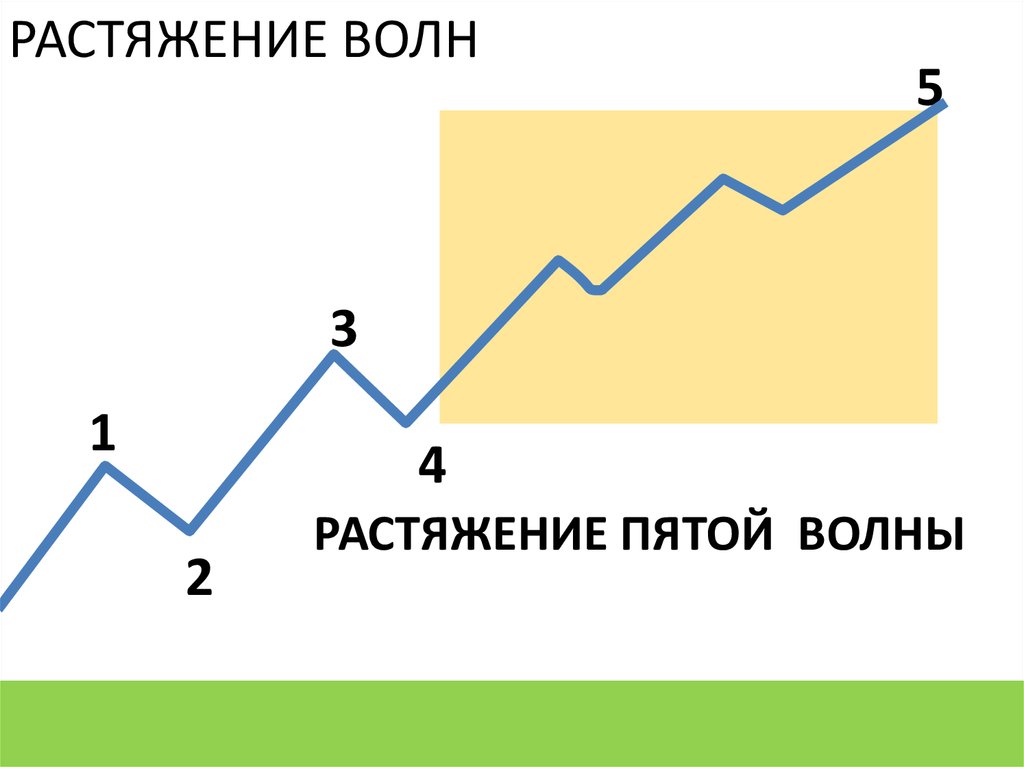
РАСТЯЖЕНИЕ ВОЛН
5
3
1
4
2
РАСТЯЖЕНИЕ ПЯТОЙ ВОЛНЫ

14.

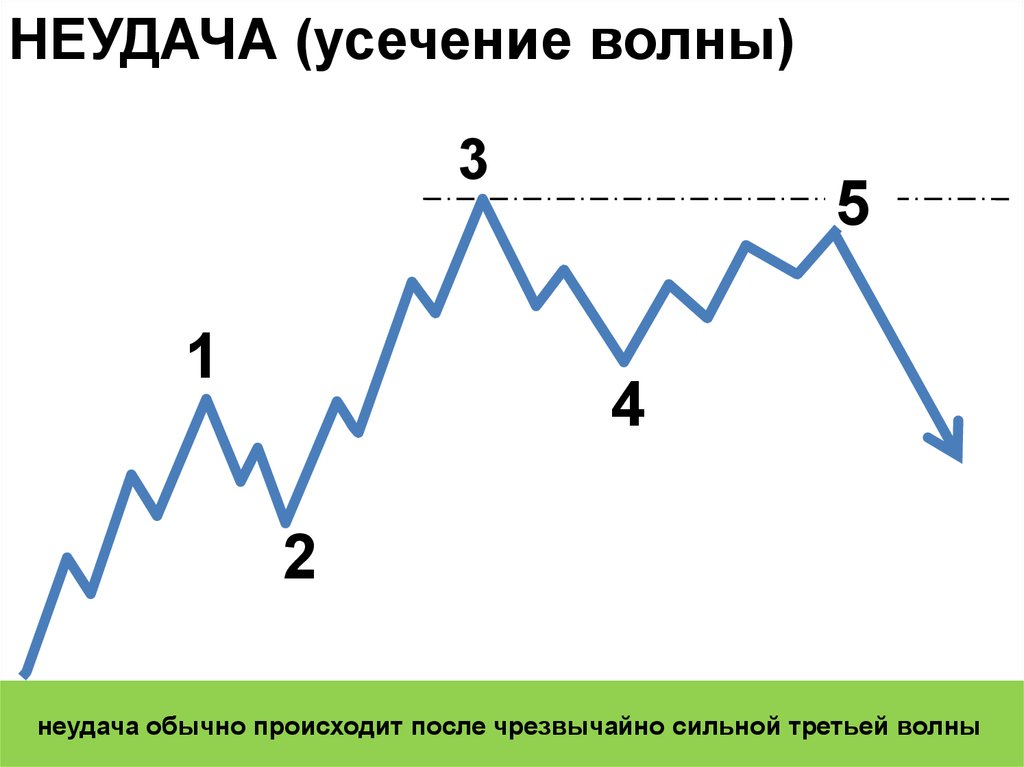
НЕУДАЧА (усечение волны)
3
1
5
4
2
неудача обычно происходит после чрезвычайно сильной третьей волны

15.

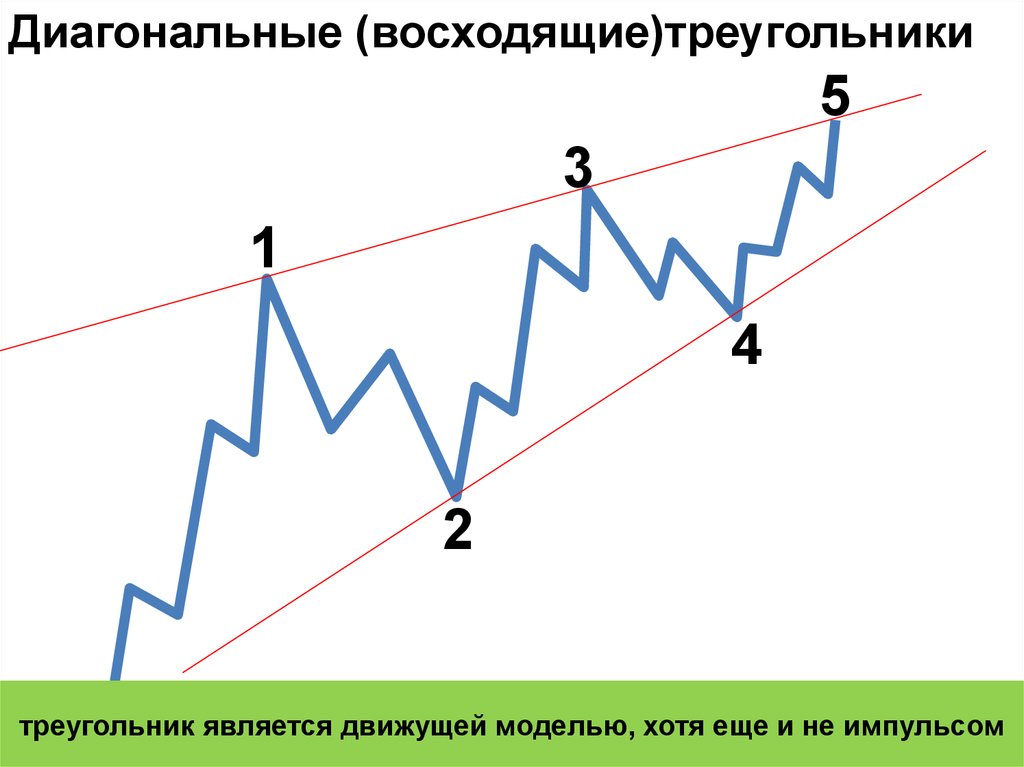
Диагональные (восходящие)треугольники
5
3
1
4
2
треугольник является движущей моделью, хотя еще и не импульсом

16.

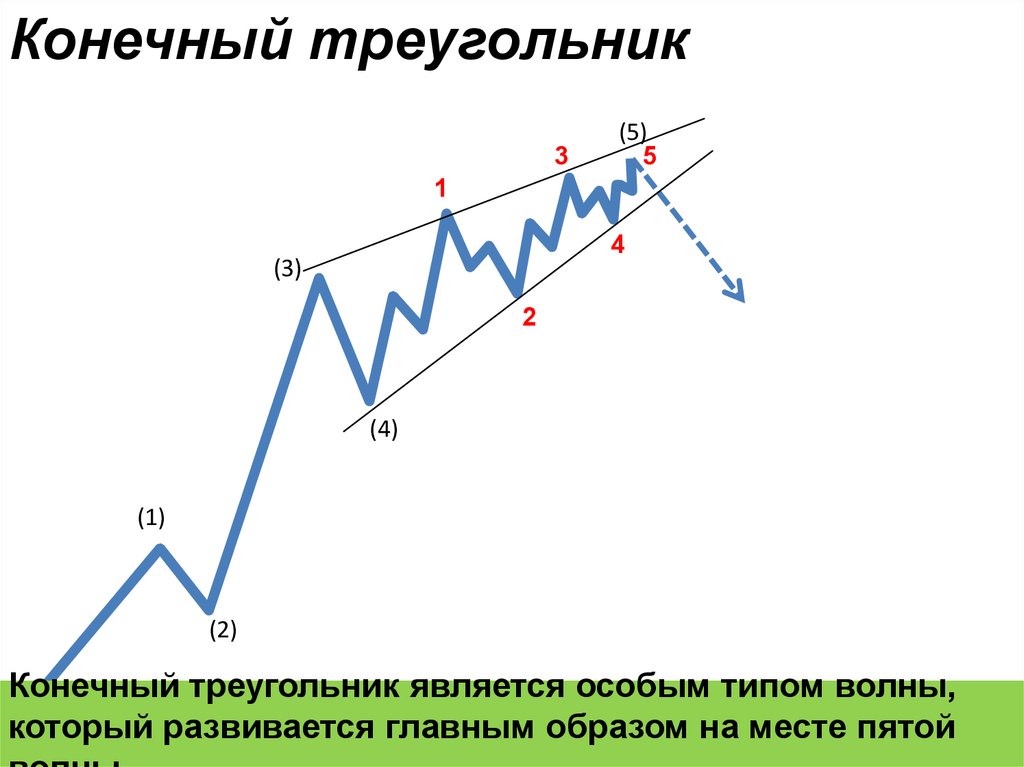
Конечный треугольник
3
(5)
5
1
4
(3)
2
(4)
(1)
(2)
Конечный треугольник является особым типом волны,
который развивается главным образом на месте пятой

17.

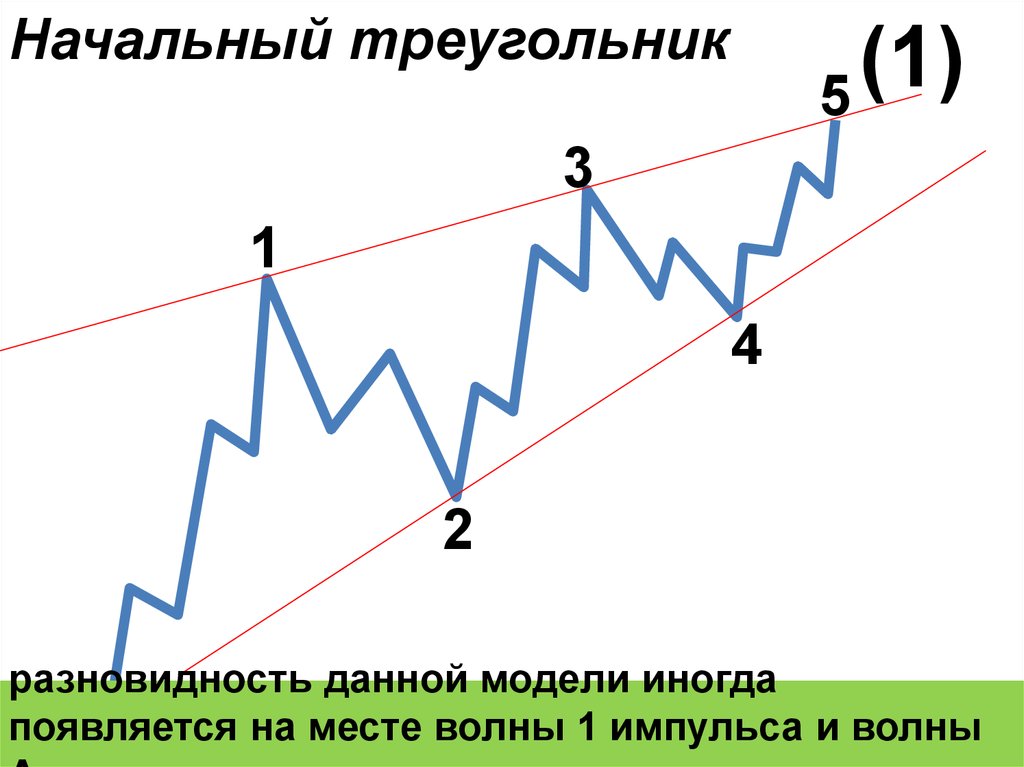
Начальный треугольник
(1)
5
3
1
4
2
разновидность данной модели иногда
появляется на месте волны 1 импульса и волны

18.

КОРРЕКТИРУЮЩИЕ ВОЛНЫ
зигзаг, плоскость, треугольник
двойная тройка, тройная двойка
откаты никогда не являются

19.

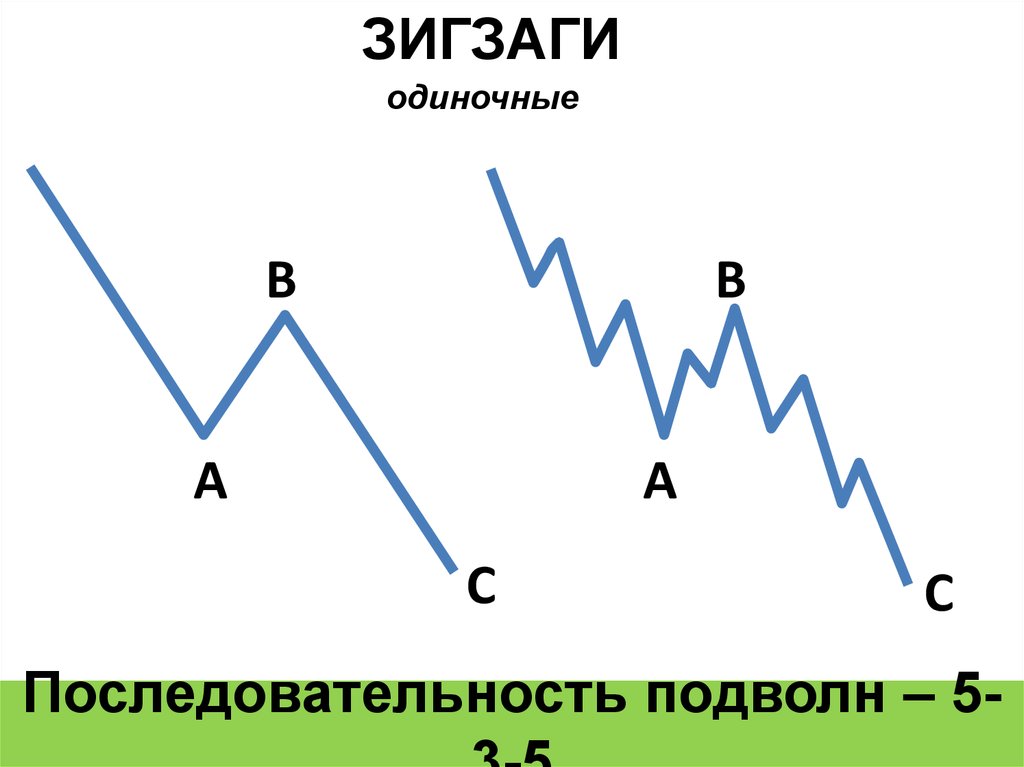
ЗИГЗАГИ
одиночные
В
В
А
А
С
С
Последовательность подволн – 5-

20.

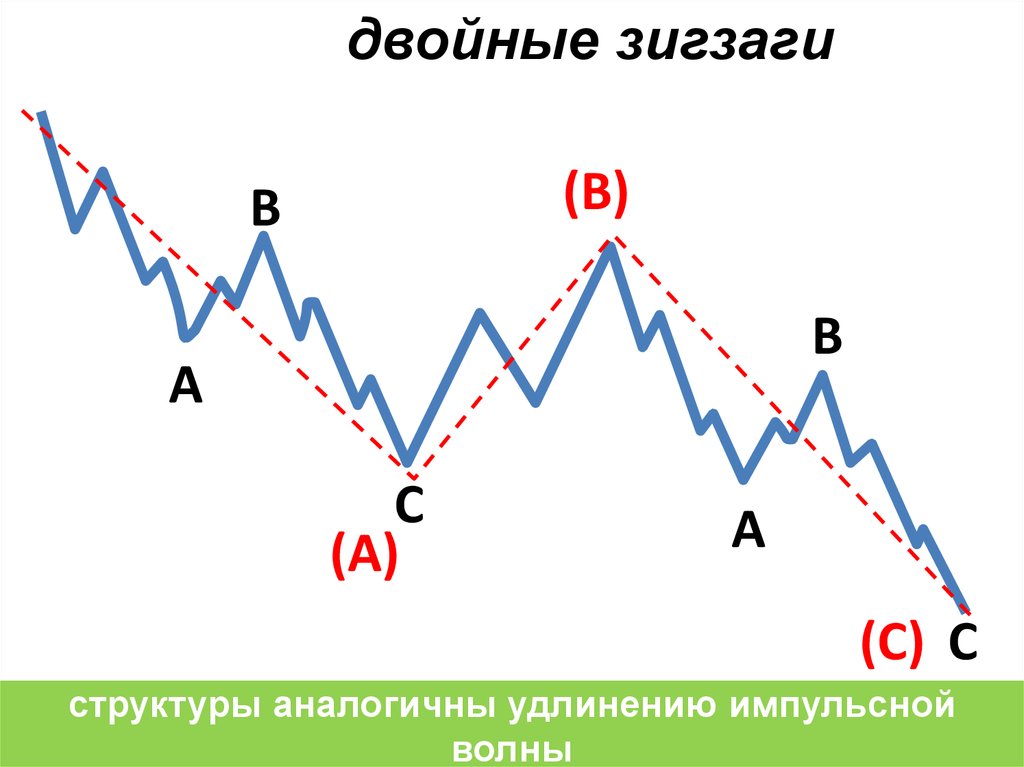
двойные зигзаги
(В)
В
В
А
С
(А)
А
(С) С
структуры аналогичны удлинению импульсной
волны

21.

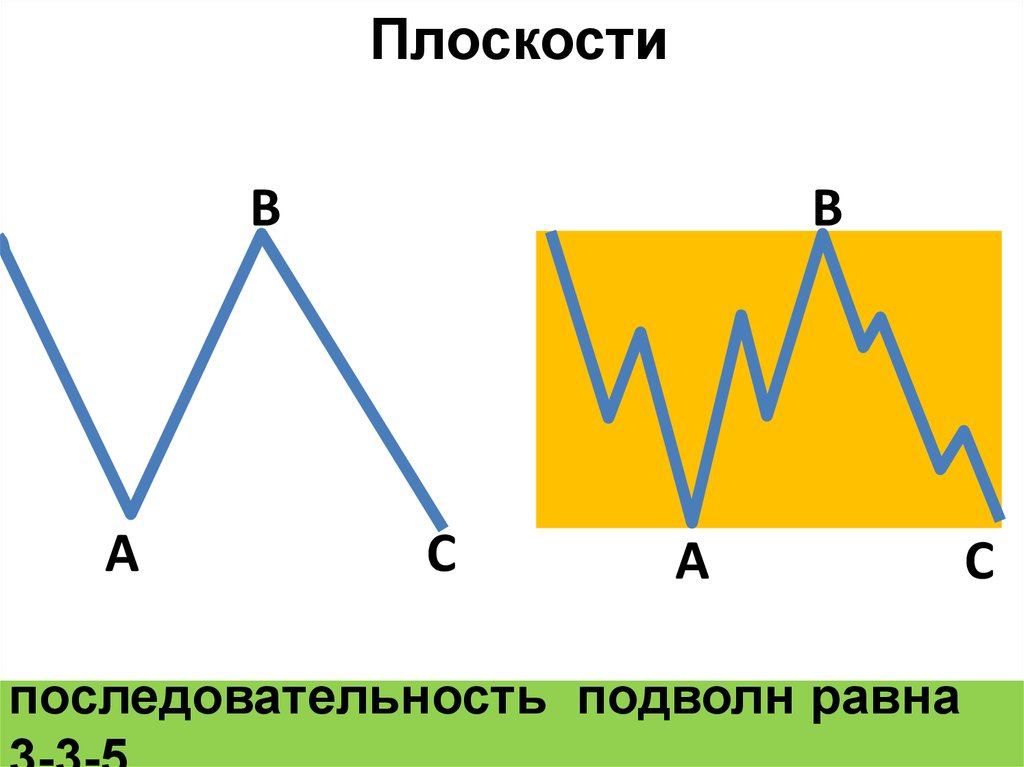
Плоскости
В
А
В
С
А
последовательность подволн равна
С

22.

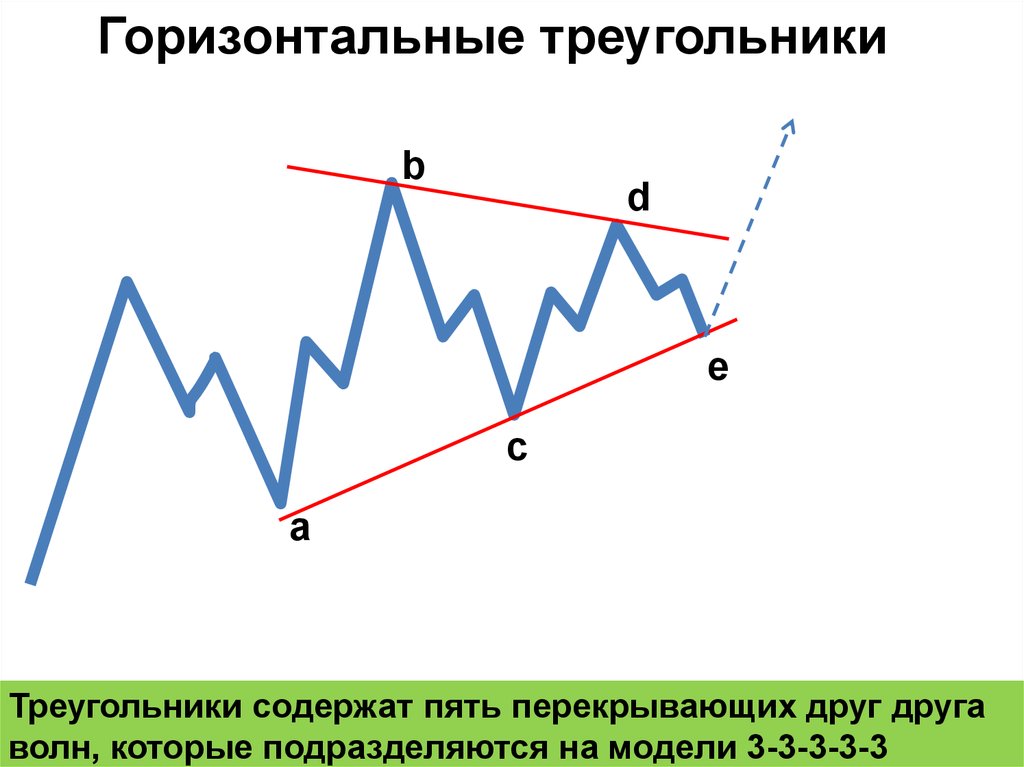
Горизонтальные треугольники
b
d
e
c
a
Треугольники содержат пять перекрывающих друг друга
волн, которые подразделяются на модели 3-3-3-3-3

23.

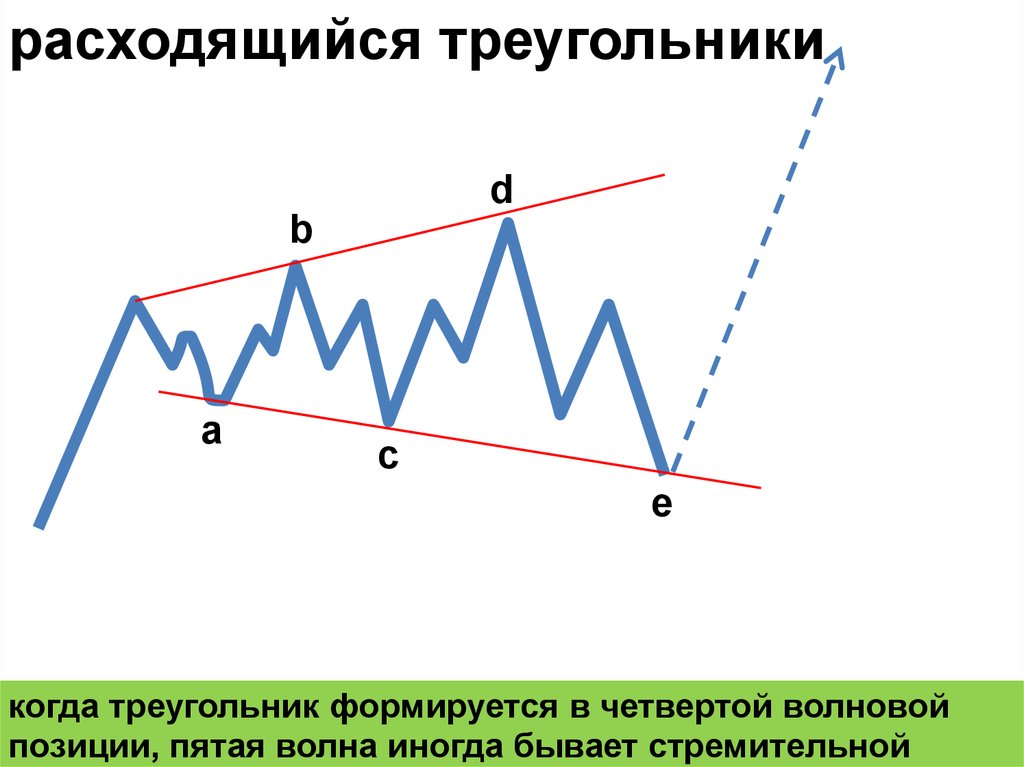
расходящийся треугольники
d
b
a
c
e
когда треугольник формируется в четвертой волновой
позиции, пятая волна иногда бывает стремительной

24.

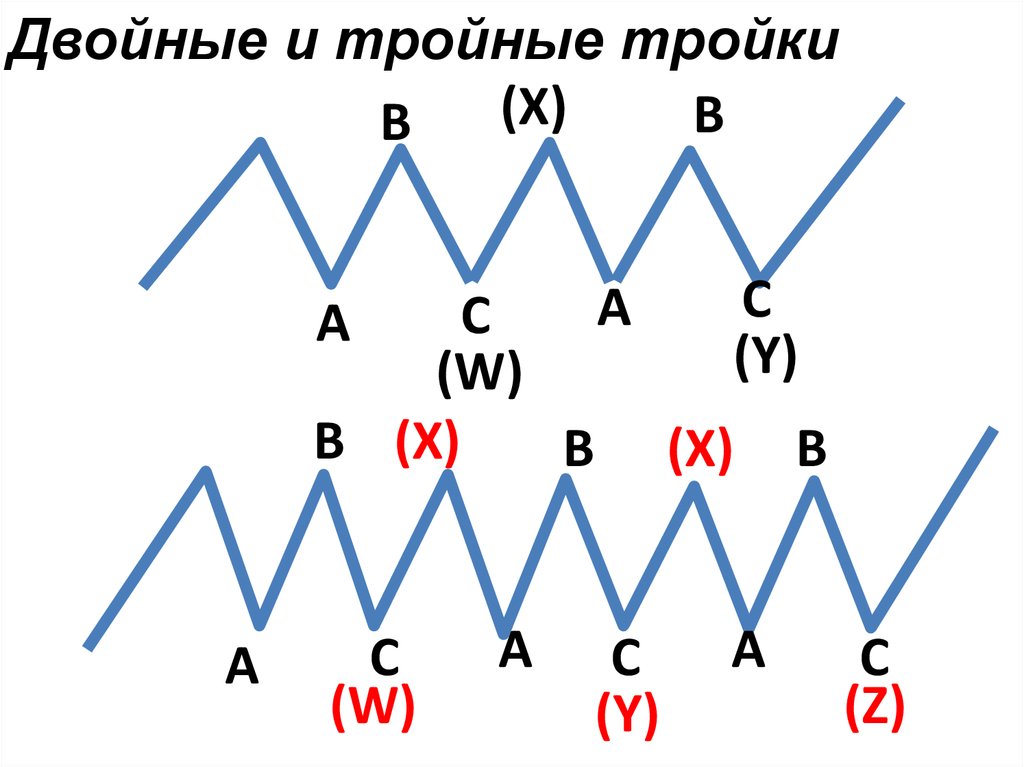
Двойные и тройные тройки
(X)
В
В
С
А
С
А
(Y)
(W)
В (X)
В (X) В
А
С
(W)
А
С
(Y)
А
С
(Z)

25.

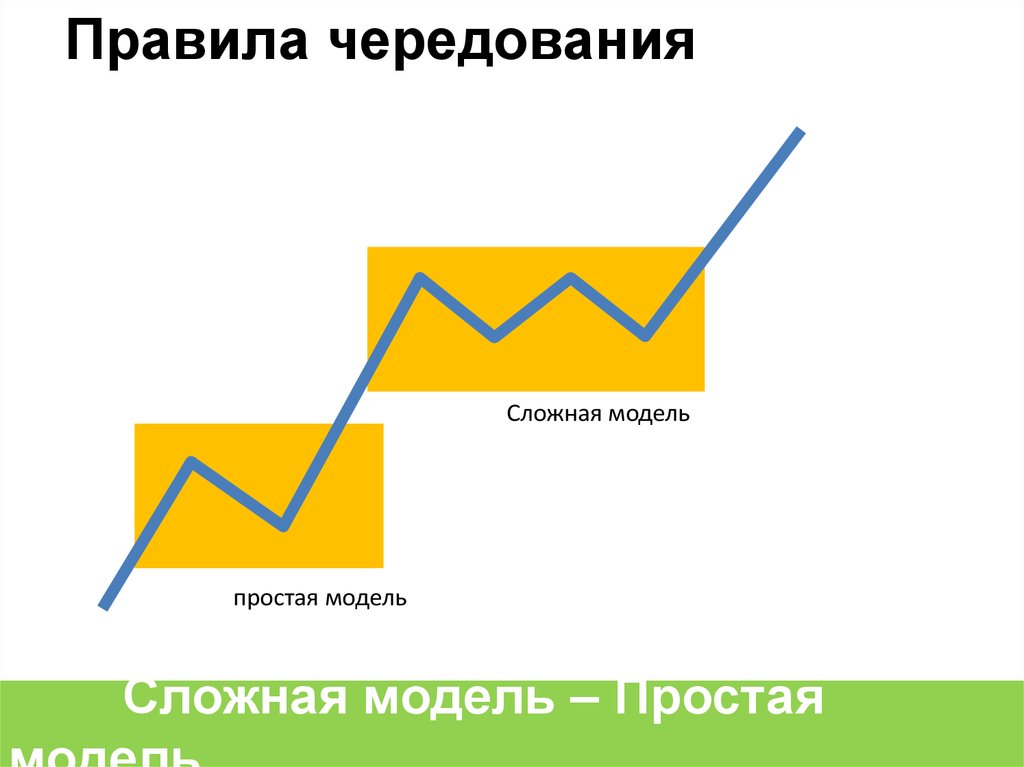
Правила чередования
Сложная модель
простая модель
Сложная модель – Простая

26.

ФИБОНАЧЧИ
Введение в мир Фибоначчи

27.

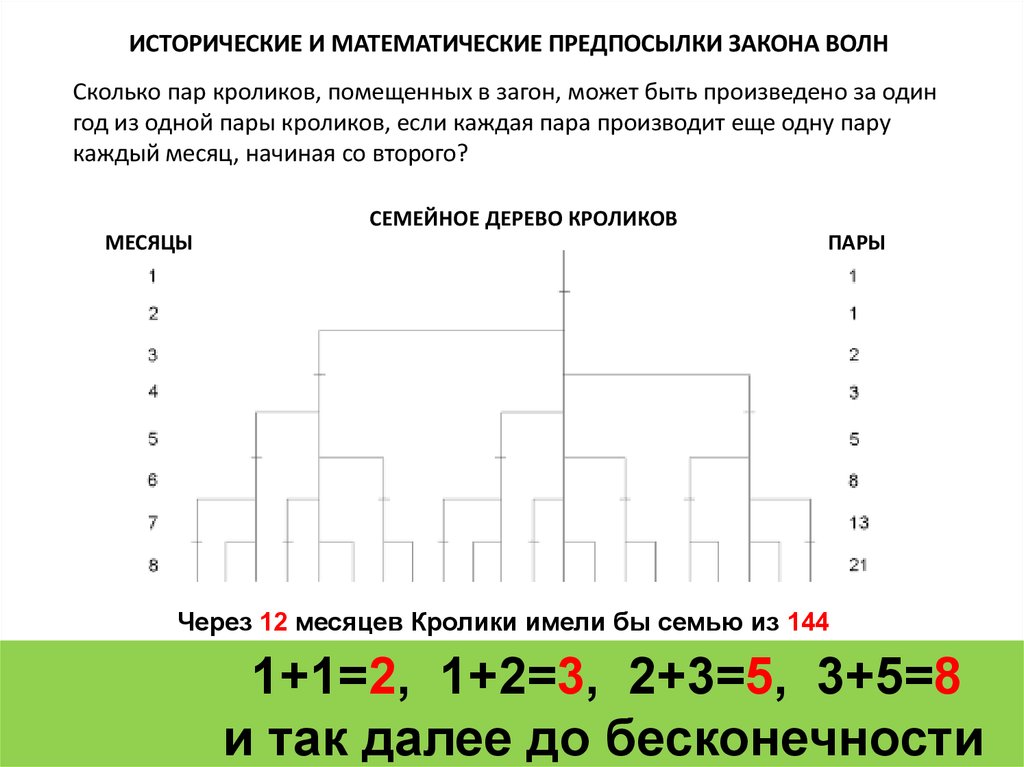
ИСТОРИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ПРЕДПОСЫЛКИ ЗАКОНА ВОЛН
Сколько пар кроликов, помещенных в загон, может быть произведено за один
год из одной пары кроликов, если каждая пара производит еще одну пару
каждый месяц, начиная со второго?
СЕМЕЙНОЕ ДЕРЕВО КРОЛИКОВ
МЕСЯЦЫ
ПАРЫ
Через 12 месяцев Кролики имели бы семью из 144
пар
1+1=2, 1+2=3, 2+3=5, 3+5=8
и так далее до бесконечности

28.

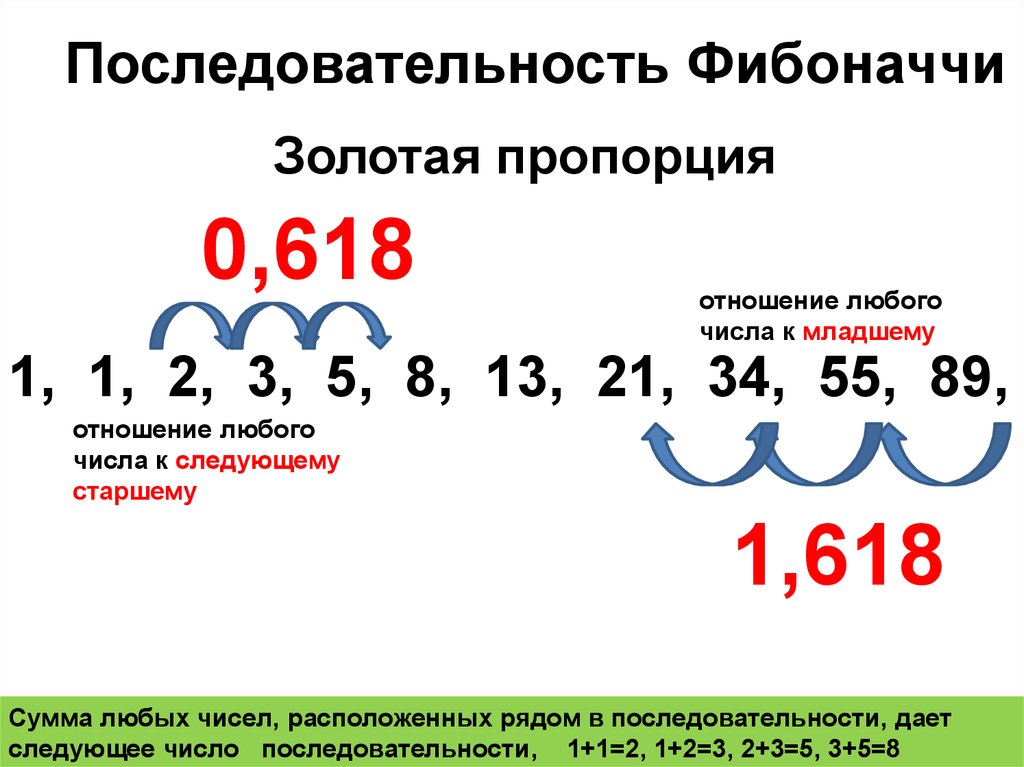
Последовательность Фибоначчи
Золотая пропорция
0,618
отношение любого
числа к младшему
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,
отношение любого
числа к следующему
старшему
1,618
Сумма любых чисел, расположенных рядом в последовательности, дает
следующее число последовательности, 1+1=2, 1+2=3, 2+3=5, 3+5=8

29.

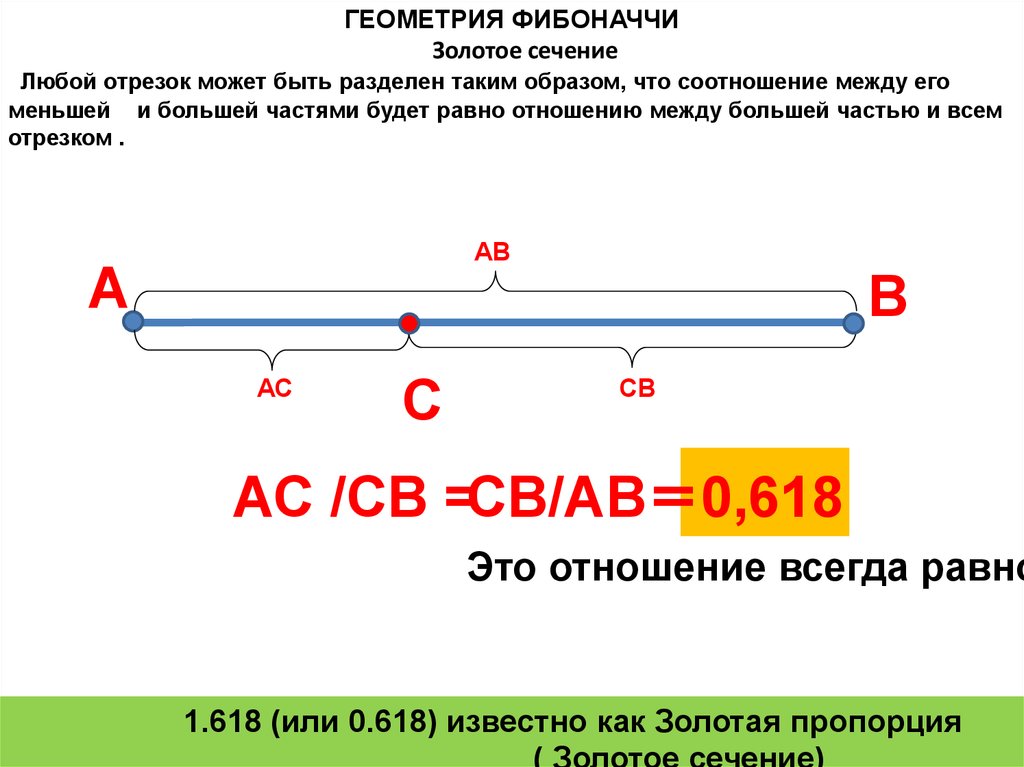
ГЕОМЕТРИЯ ФИБОНАЧЧИ
Золотое сечение
Любой отрезок может быть разделен таким образом, что соотношение между его
меньшей и большей частями будет равно отношению между большей частью и всем
отрезком .
АВ
А
АС
С
В
СВ
АС /СВ =СВ/АВ == 0,618
Это отношение всегда равно
1.618 (или 0.618) известно как Золотая пропорция
( Золотое сечение)

30.

31.

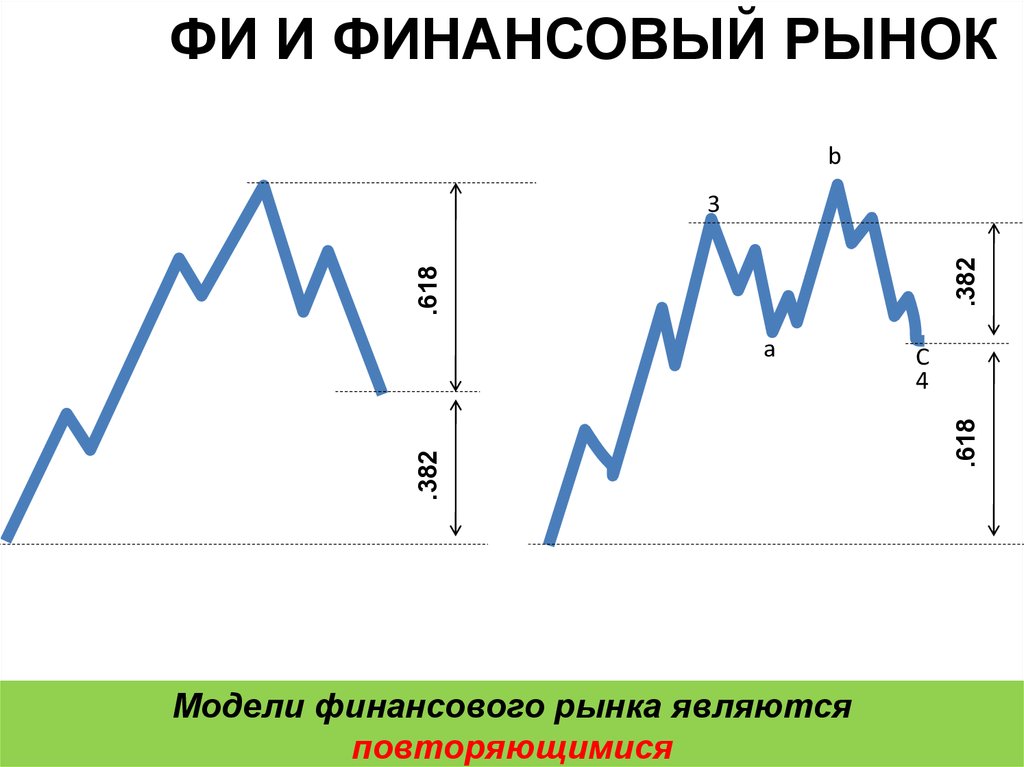
ФИ И ФИНАНСОВЫЙ РЫНОК
b
.618
.382
3
Модели финансового рынка являются
повторяющимися
C
4
.618
.382
а

32.

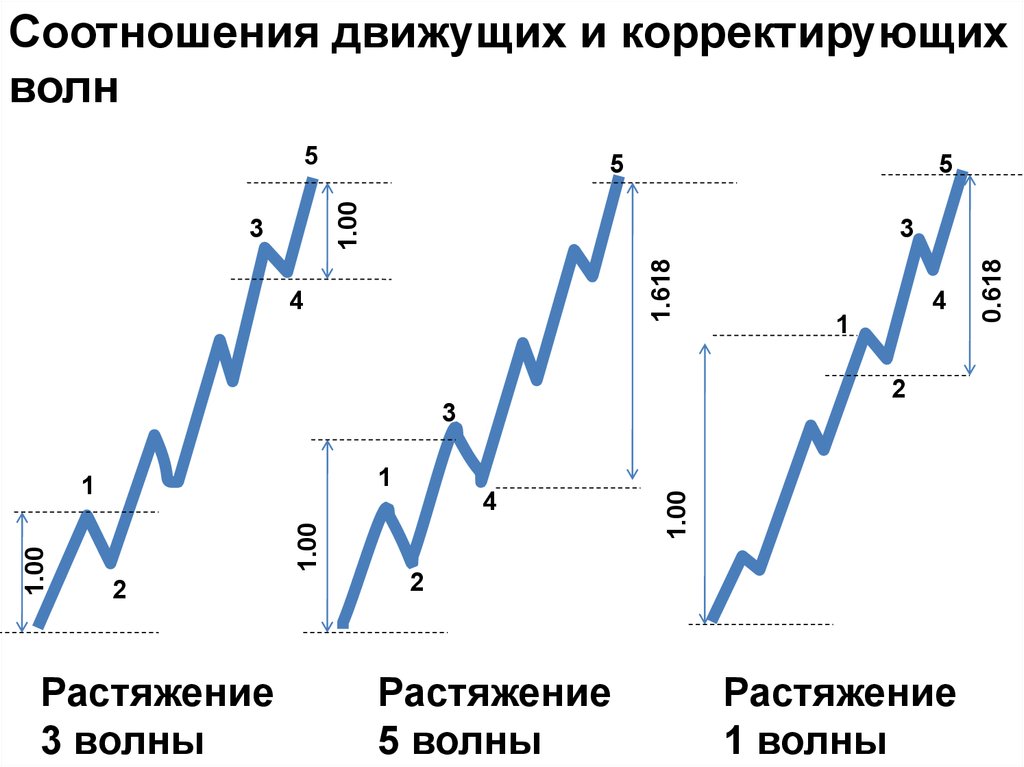
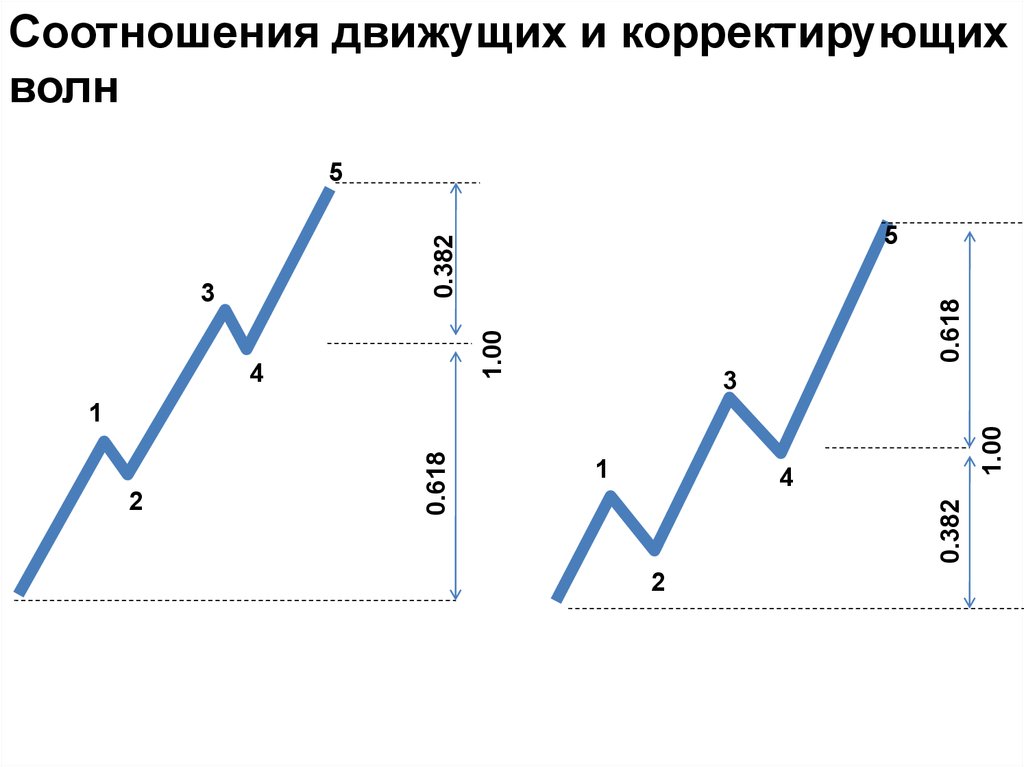
Соотношения движущих и корректирующих
волн
5
5
1.00
5
4
4
1
2
1
4
1.00
1.00
1
2
Растяжение
3 волны
1.00
3
2
Растяжение
5 волны
Растяжение
1 волны
0.618
3
1.618
3

33.

Соотношения движущих и корректирующих
волн
5
1.00
3
0.618
0.382
5
4
3
1.00
1
4
0.382
2
0.618
1
2

34.

Спасибо за участие в семинаре!
Мы желаем Вам успехов!

35. фракталы

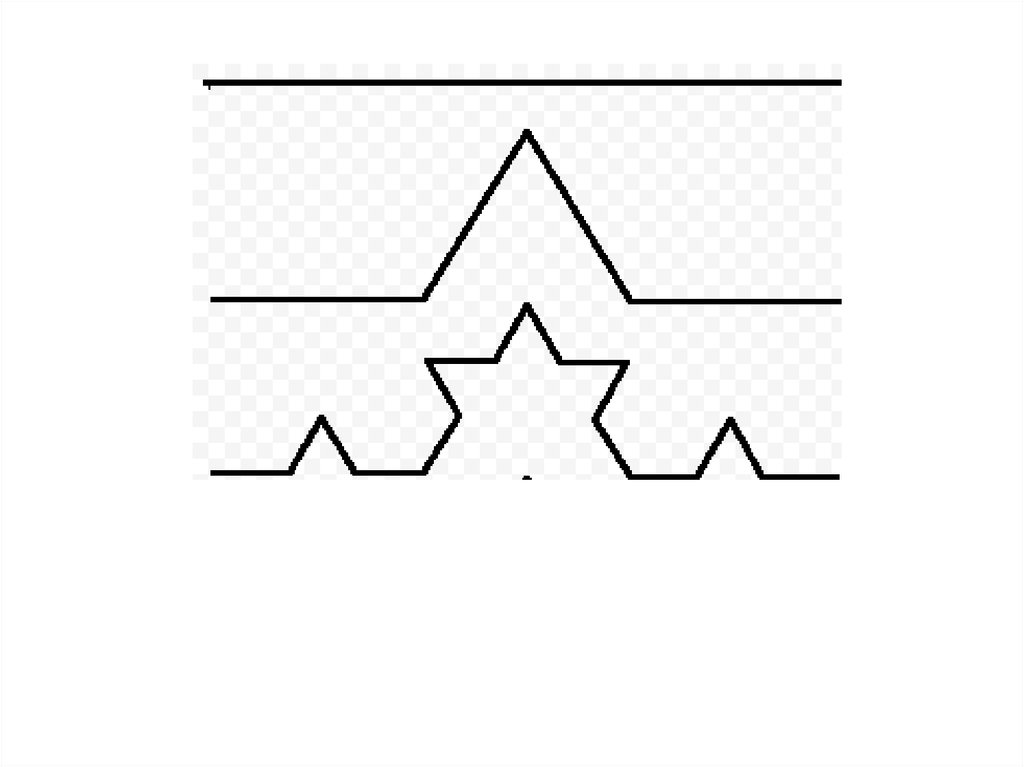
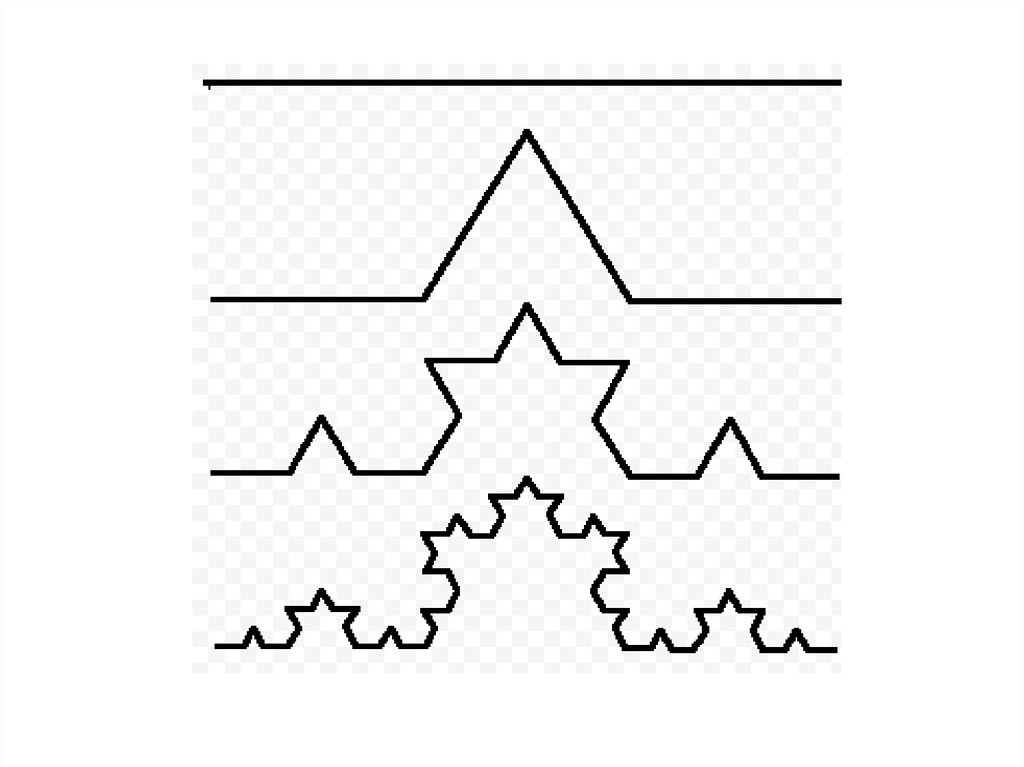
Fractals
Фрактал (. fractus — дроблёный, сломанный, разбитый) — математическое
множество, обладающее свойством САМОПОДОБИЯ
(объект, в точности или приближённо совпадающий с частью себя самого, то есть
целое имеет ту же форму, что и одна или более частей).

36.

37.

38.

39.

40.

41.

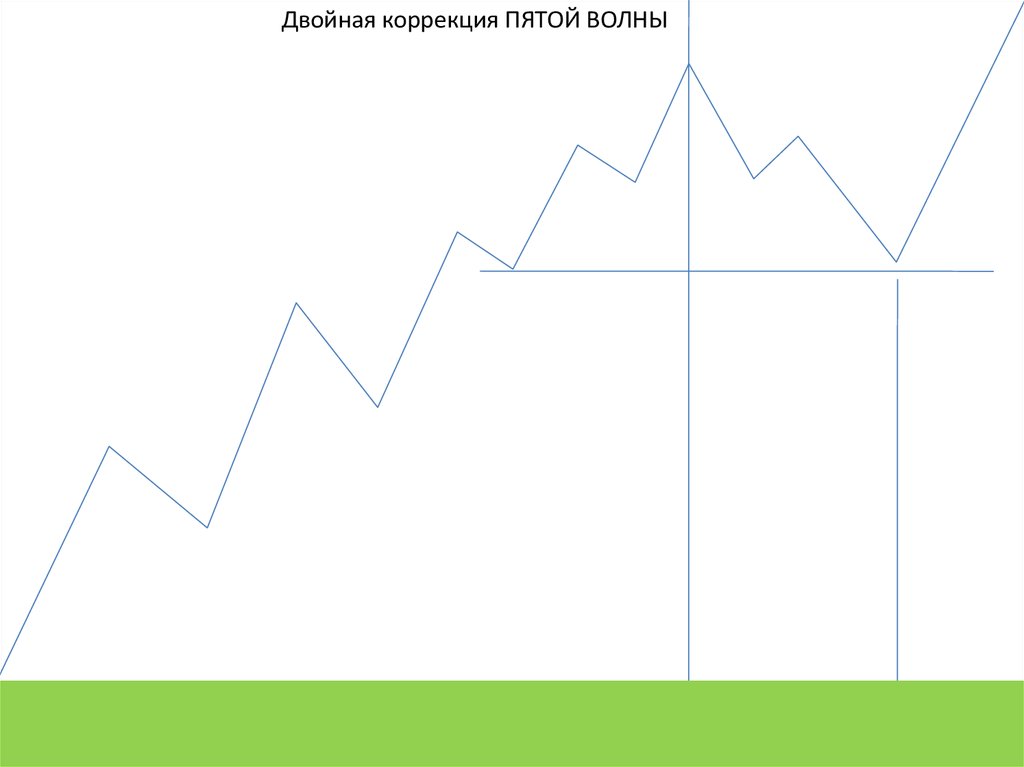
Двойная коррекция ПЯТОЙ ВОЛНЫ

42.

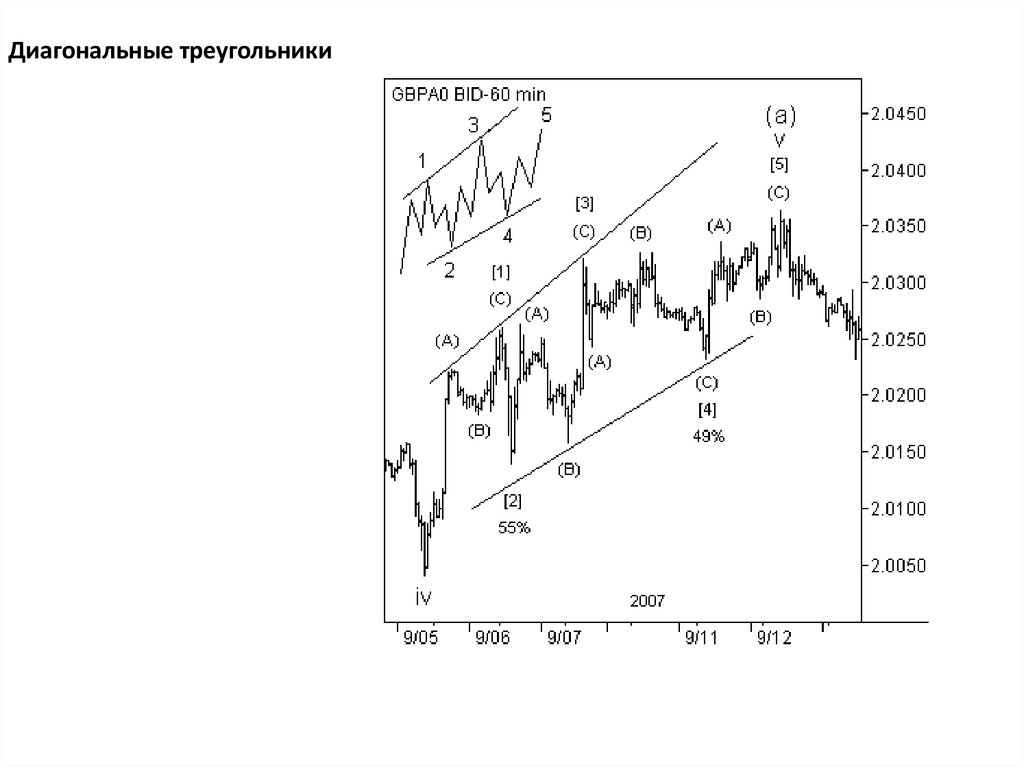
Диагональные треугольники

43.

44.

45.

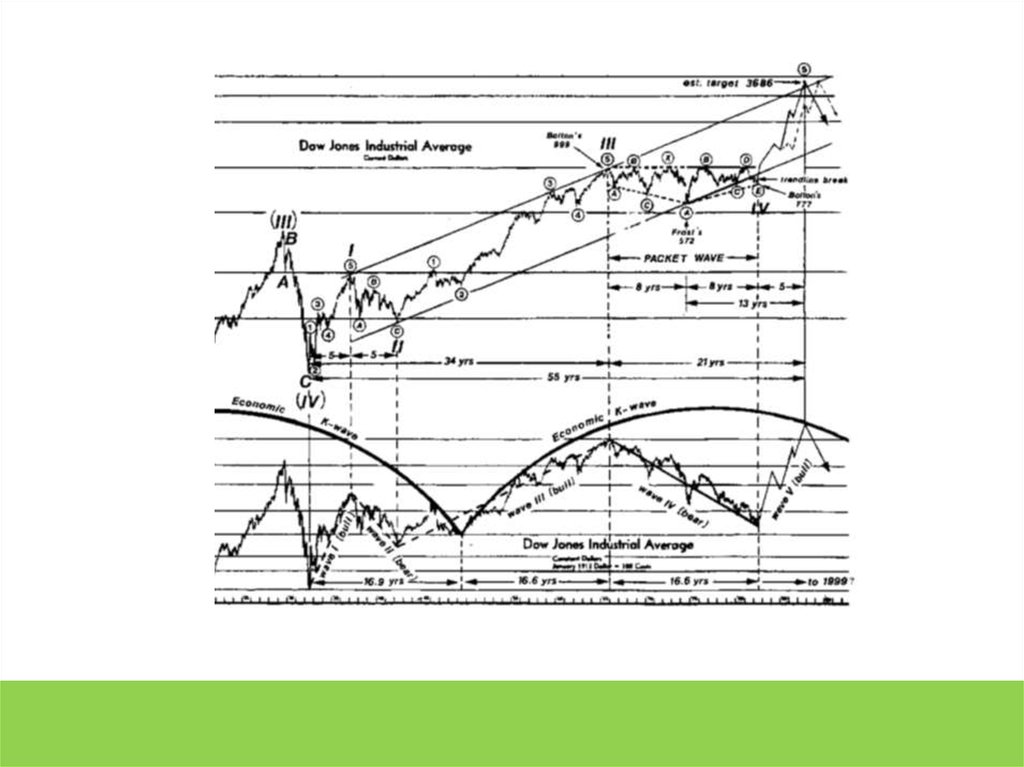
Прехтер и его система разметки.
Общие правила
Топография волновой карты

46.

3 правила, считающиеся "нерушимыми"

47.

Импульс

48.

Клинья (Wedges)