Похожие презентации:
Кинематика твердого тела
1. Кинематика твердого тела
1. Теорема о поступательномдвижении тела.
2. Параметры вращательного
движения.
3. Законы вращения.
4. Сложное движение тела.
2.
3. При поступательном движении любая прямая, связанная с телом, движется параллельно своему первоначальному положению.
Теорема: «При поступательномдвижении все точки твердого тела
имеют одинаковые траектории,
скорости и ускорения.»
4. 2, При вращательном движении хотя бы две точки остаются неподвижны, через них проходит ось вращения.
Угол, на которыйповернется тело за
некоторое время
называется углом
поворота тела.
f (t ) уравнениевращения
2 N об ( рад)
N об количество оборотов
а
а
5.
Угловая скорость тела в данный моментвремени равна первой производной от угла
поворота по времени:
d рад
(
)
dt
с
n
30
n частота вращениятела(об / мин )
Угловое ускорение в данный момент времени
равно первой производной от угловой скорости по
времени:
d рад
( 2 )
dt
с
6. Связь между угловыми и линейными параметрами движения
Линейная скорость:R
Касательное ускорение:
а R
Линейное перемещение:
S R
Нормальное ускорение:
аn R
2
7. 3. Законы вращения
Закон равномерного вращения:0 t
Закон равнопеременного вращения:
0 0 t
t
2
2
Угловая скорость при равнопеременном
вращении:
0 t
8. 4, Сложное движение твердого тела можно рассматривать, как совокупность относительного и переносного движения.
Плоскопараллельное движение – это примерсложного движения тела. При плоскопараллельном
движении все точки тела движутся в плоскостях,
параллельных данной.
Такой вид движения используют в плоских
механизмах.
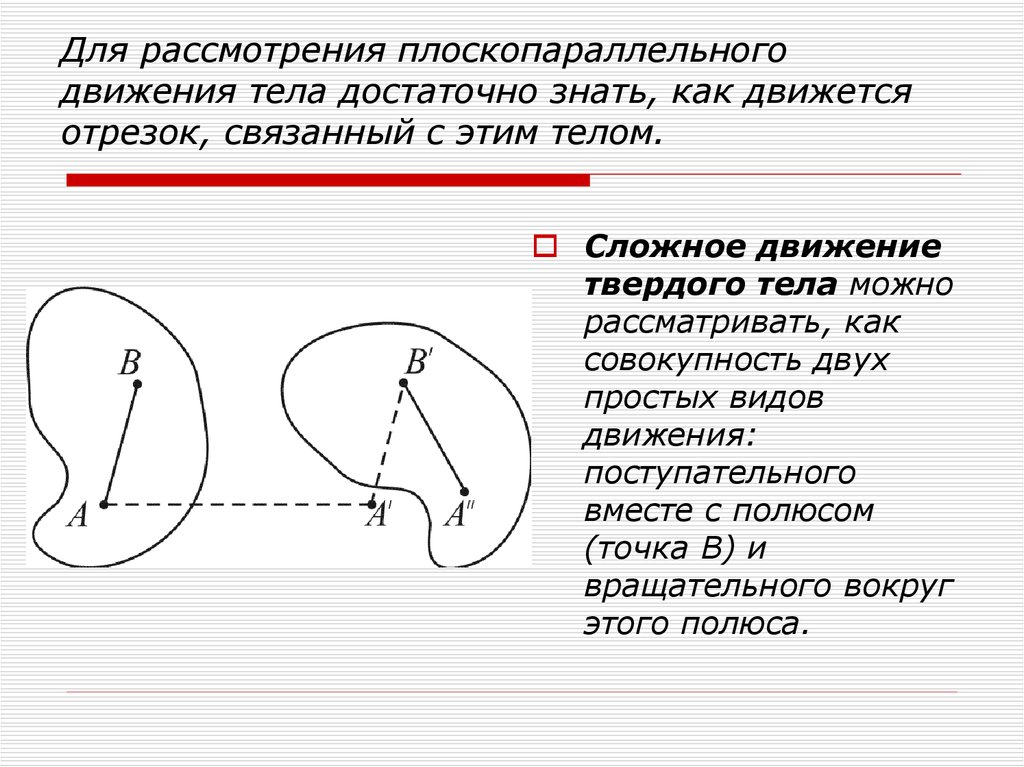
9. Для рассмотрения плоскопараллельного движения тела достаточно знать, как движется отрезок, связанный с этим телом.
Сложное движениетвердого тела можно
рассматривать, как
совокупность двух
простых видов
движения:
поступательного
вместе с полюсом
(точка В) и
вращательного вокруг
этого полюса.
10. Метод разложения скоростей при сложном движении тела
Скорость любой точкиплоской фигуры равна
геометрической сумме
двух скоростей:
скорости полюса
(точка А) и
вращательной скорости
вокруг этого полюса.
В А ВА








 Физика
Физика








