Похожие презентации:
Способы решения логических задач
1.
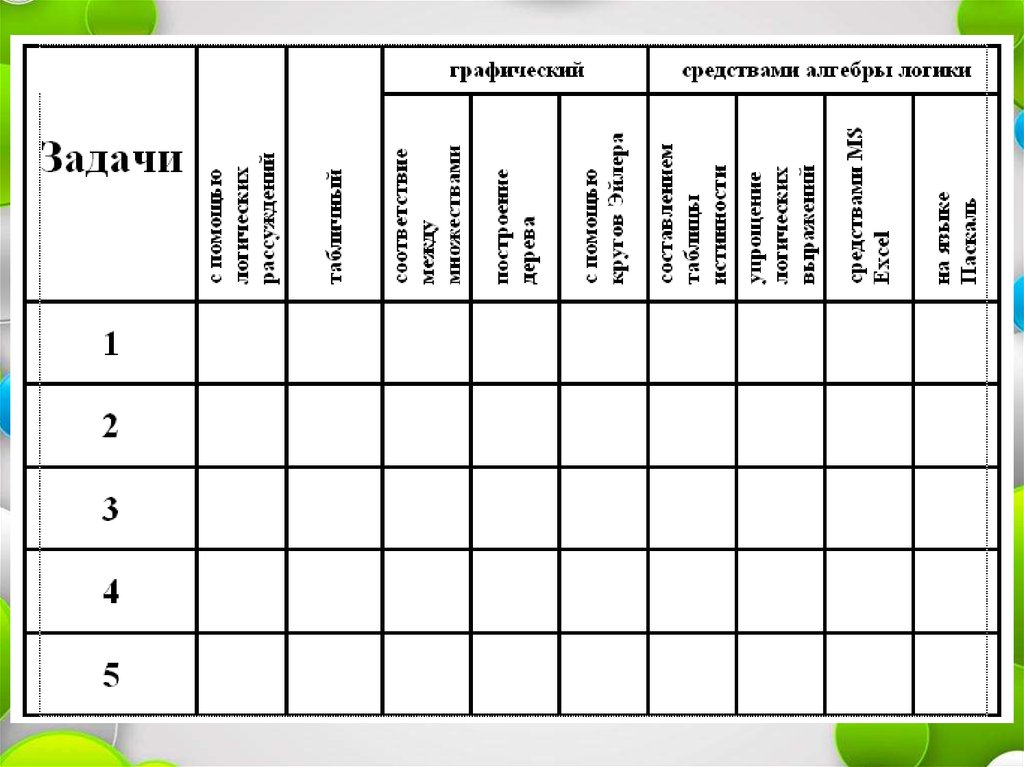
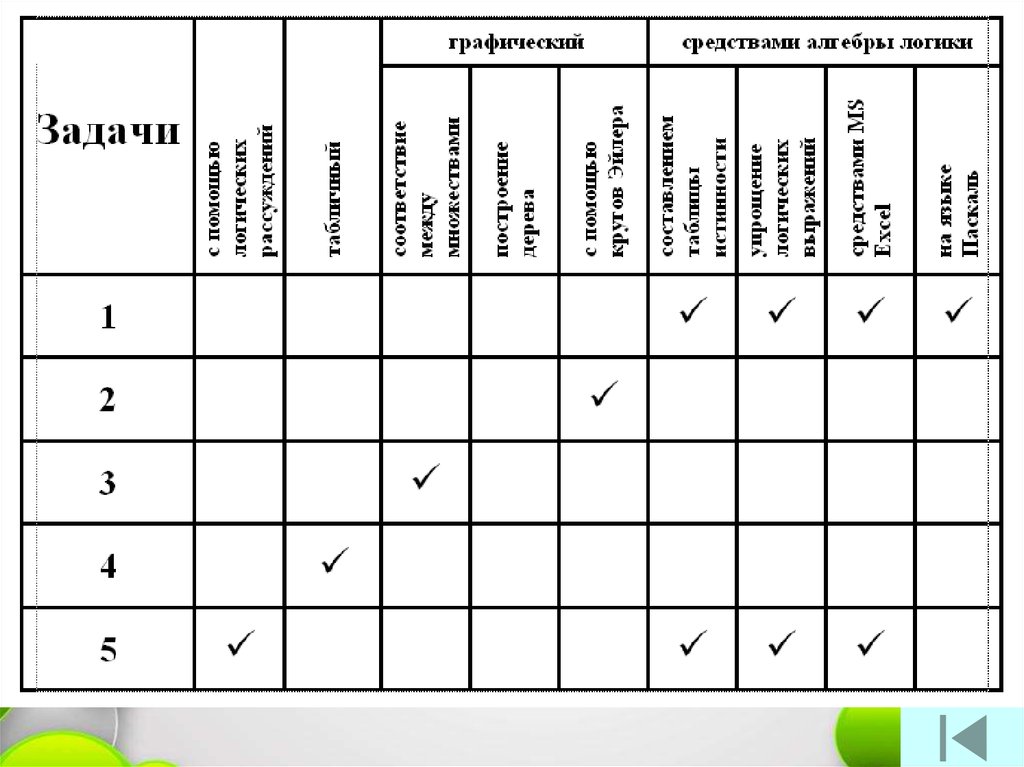
2. Способы решения логических задач:
1)с помощью логических рассуждений;
2)
табличный;
3)
графический ;
4)
a)
графический (соответствие между множествами)
b)
графический (построение дерева)
c)
с помощью кругов Эйлера
средствами алгебры логики;
a)
составлением таблицы истинности;
b)
упрощение логических выражений (по законам логики);
упрощение логических выражений (задача про кросс);
c)
на ЭВМ составлением таблицы истинности средствами MS
Excel;
d)
на ЭВМ ( алгоритм, на языке Паскаль).
Составь блок - схему
3. Метод рассуждений
При составлении расписания на понедельник в IXклассе преподаватели высказали просьбу завучу.
1. Учитель математики: «Желаю иметь первый или
второй урок».
2. Учитель истории: «Желаю иметь первый или
третий урок».
3. Учитель литературы: «Желаю иметь второй или
третий урок».
Какое расписание будет составлено, если по каждому
предмету может быть только один урок?
4. Решение
• Пусть в просьбе математика первоевысказывание истинно, а второе – ложно.
«Желаю иметь первый или второй урок».
1
0
Т.е. первым будет урок математики.
• Тогда в просьбе учителя истории первое
высказывание ложно, а второе истинно, т.е.
третьим будет урок истории. «Желаю иметь
первый или третий урок».
0
1
• Значит, в пожелании учителя литературы
окажется истинной первая часть, т.е. урок
литературы будет вторым.
«Желаю иметь второй или третий урок».
1
Итак:
0
I урок – математика,
II урок – литература,
III урок – история.
5.
типызадач
Предположим, что в высказывании учителя математики
первое высказывание ложно, а второе истинно.
«Желаю иметь второй или второй урок».
0
1
Т.е. вторым будет урок математики.
Тогда в просьбе учителя литературы первое высказывание
ложно, а второе истинно, т.е. третьим будет урок
литературы.
«Желаю иметь второй или третий урок».
0
1
А в пожелании учителя истории окажется истинной первая
часть, т.е. урок истории будет первым.
«Желаю иметь первый или третий урок».
1
0
Итак:
I урок - история
II урок - математика
III урок – литература.
6.
В лесу проводили кросс. Обсуждая его итоги, однаБелка сказала:
«Заяц занял первое место, а лиса-второе».
Другая Белка возразила:
«Заяц занял второе место, а лось – первое».
На что Филин заметил, что в высказываниях
каждой Белки одна часть верная, а другая – нет. Кто
был первым в этом кроссе?
7.
Выделим высказыванияВ лесу проводили кросс. Обсуждая его итоги, одна Белка
сказала:
«Заяц занял первое место, а лиса-второе».
Другая Белка возразила:
«Заяц занял второе место, а лось – первое».
На что Филин заметил, что в высказываниях каждой Белки
одна часть верная, а другая – нет.
Кто был первым в этом кроссе?
8.
Предположим, что в первом предложенииистинно
Пусть высказывание
1-я белка:
истинно
«Заяц занял первое место, а лиса-второе».
2-я белка:
«Заяц занял второе место, а лось – первое».
В результате исходного предположения мы
пришли к противоречию. Заяц не может занять
второе место – это ложь. Лось не может быть
первым - это ложь. В высказываниях каждой
Белки одна часть верная, а другая – нет.
9.
Предположим, что в первом предложенииистинно
Пусть высказывание
1-я белка:
истинно
«Заяц занял первое место, а лиса-второе».
Высказывание ложно
Высказывание
истинно
2-я белка:
«Заяц занял второе место, а лось – первое».
В результате исходного предположения
противоречия нет!!!
Ответ: первым в этом кроссе был лось
10.
В лесу проводили кросс. Обсуждая его итоги, однаБелка сказала: «Заяц занял первое место, а лисавторое». Другая Белка возразила: «Заяц занял
второе место, а лось – первое». На что Филин
заметил, что в высказываниях каждой Белки одна
часть верная, а другая – нет. Кто был первым в этом
кроссе?
Введем простые высказывания
З1- заяц 1 место
З2 - заяц 2 место
Лс1- лось 1 место
Л2 - лиса 2 место
Составим логические выражения
1-я белка: З1 Л2
2-я белка: З2 Лс1
(З1 Л2) (З2 Лс1)=1; (З1+Л2) (З1+Лс1)=1;
11.
В лесу проводили кросс. Обсуждая его итоги, одна Белка сказала:«Заяц занял первое место, а лиса-второе». Другая Белка
возразила: «Заяц занял второе место, а лось – первое». На что
Филин заметил, что в высказываниях каждой Белки одна часть верная,
а другая – нет. Кто был первым в этом кроссе?
(З1 Л2) (З2 Лс1)=1;
(З1+Л2)
(З1+Лс1)=1;
Раскроем скобки З1З2+Л2З2+З1Лс1+Л2Лс1=1;
Логическое умножение заведомо противоречивых
высказываний З1З2=0
Аналогично, Л2З2=0, З1Лс1=0.
З1З2+Л2З2+З1Лс1+Л2Лс1=1; Получим
Л2Лс1=1; Только в одном случае Л2=1 и Лс=1
Значит, Лось - 1 место, Лиса – 2 место.
Ответ: первым в этом кроссе был лось
12.
Задача «Уроки логики»Если изучал первый, то изучал и второй, но
неверно, что если изучал третий, то изучал и
второй. Кто изучал логику?
Введем простые высказывания
Р1- первый изучал логику
Р2- второй изучал логику
Р3- третий изучал логику
Составим высказывание, выражающее
известные факты в условии задачи:
(Р1 →Р2) ¬(Р3 →Р2)
Составим таблицу истинности на
основании сформулированных простых и
составных высказываний
13.
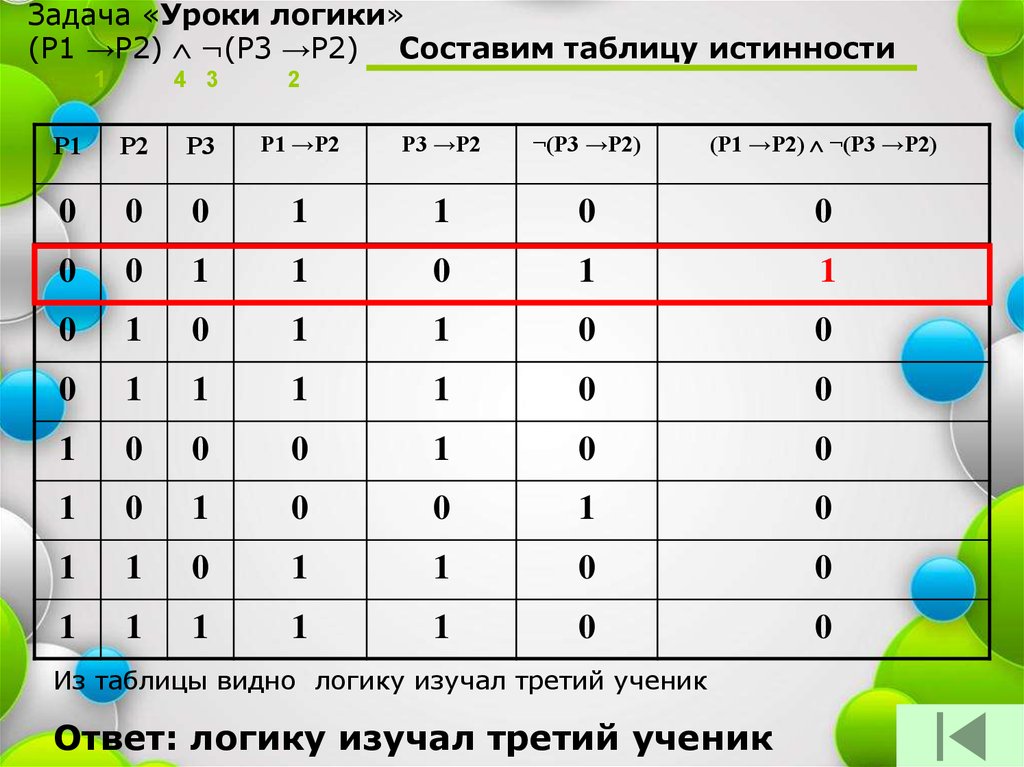
Задача «Уроки логики»(Р1 →Р2) ¬(Р3 →Р2) Составим таблицу истинности
1
4 3
2
Р1
Р2
Р3
Р1 →Р2
Р3 →Р2
¬(Р3 →Р2)
(Р1 →Р2) ¬(Р3 →Р2)
0
0
0
1
1
0
0
0
0
1
1
0
1
1
0
1
0
1
1
0
0
0
1
1
1
1
0
0
1
0
0
0
1
0
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
1
1
1
1
1
0
0
Из таблицы видно логику изучал третий ученик
Ответ: логику изучал третий ученик
14. Задача «Уроки логики»
(Р1 →Р2) ¬(Р3 →Р2) = 1Используем формулу замены операций А →В=¬А В
(Р1 →Р2) ¬(Р3 →Р2)=(¬ Р1+ Р2) (¬(¬ Р3+ Р2))=
{закон де Моргана, закон двойного отрицания}=
(¬ Р1+ Р2) ¬ Р2 Р3= {закон дистрибутивности}=
¬ Р1 ¬ Р2 Р3+ Р2 ¬ Р2 Р3=
{можно опустить знаки умножения(конъюнкция)}
= ¬ Р1¬ Р2 Р3+ Р2 ¬ Р2 Р3=
{закон противоречия}= ¬ Р1¬ Р2 Р3 = 1;
¬ Р1¬ Р2 Р3 = 1;
Получили уравнение вида « произведение равно 1», в
нем все множители должны быть равны 1
Поэтому Р1=0, Р2=0, Р3=1
Ответ: логику изучал третий ученик
15. Установим соответствие между элементами различных множеств
Способы решения:табличный;
графический.
В кафе встретились три друга: скульптор
Белов, скрипач Чернов и художник Рыжов.
«Замечательно,что у одного из нас белые,у
другого черные ,а у третьего рыжие
волосы,но ни у кого цвет волос не
соответствует фамилии»,-заметил
черноволосый. «Ты прав»,- сказал Белов.
Какого цвета волосы у художника.
16. Графический способ решения
«Ни у кого цвет волос не соответствует фамилии»заметил черноволосый. «Ты прав»,- сказал Белов
Белов не черноволосый
Белов
черные
Рыжов
белые
Чернов
рыжие
17. Графический способ решения
Белов может быть только рыжеволосымБелов
черные
Рыжов
белые
Чернов
рыжие
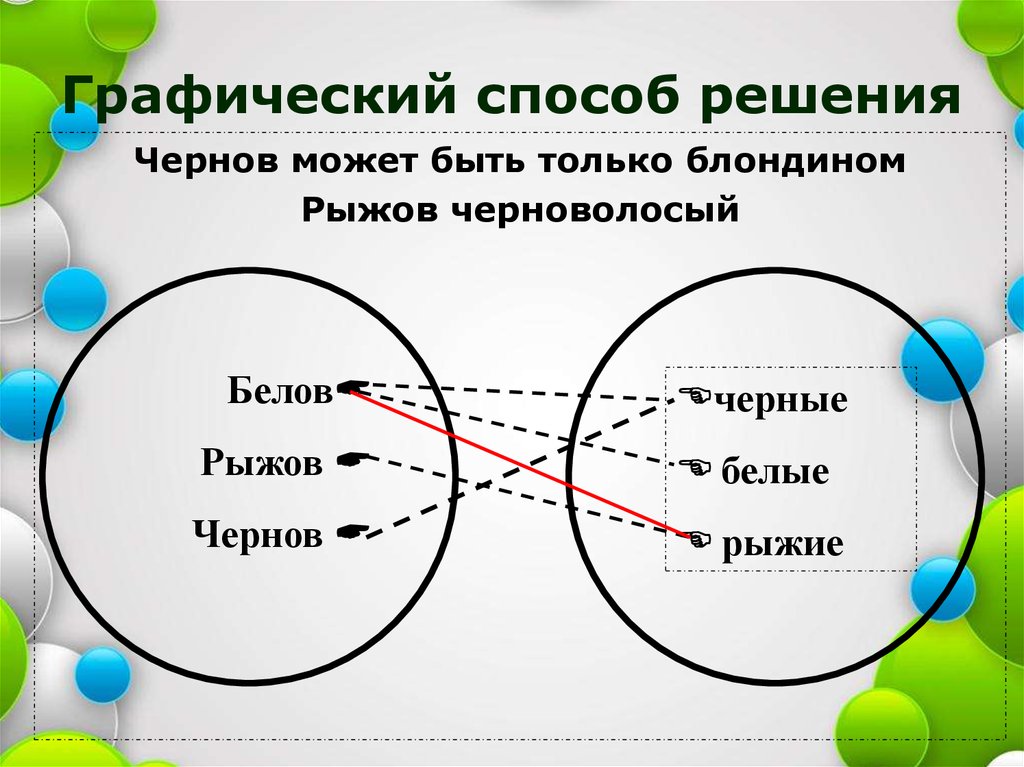
18. Графический способ решения
Чернов может быть только блондиномРыжов черноволосый
Белов
черные
Рыжов
белые
Чернов
рыжие
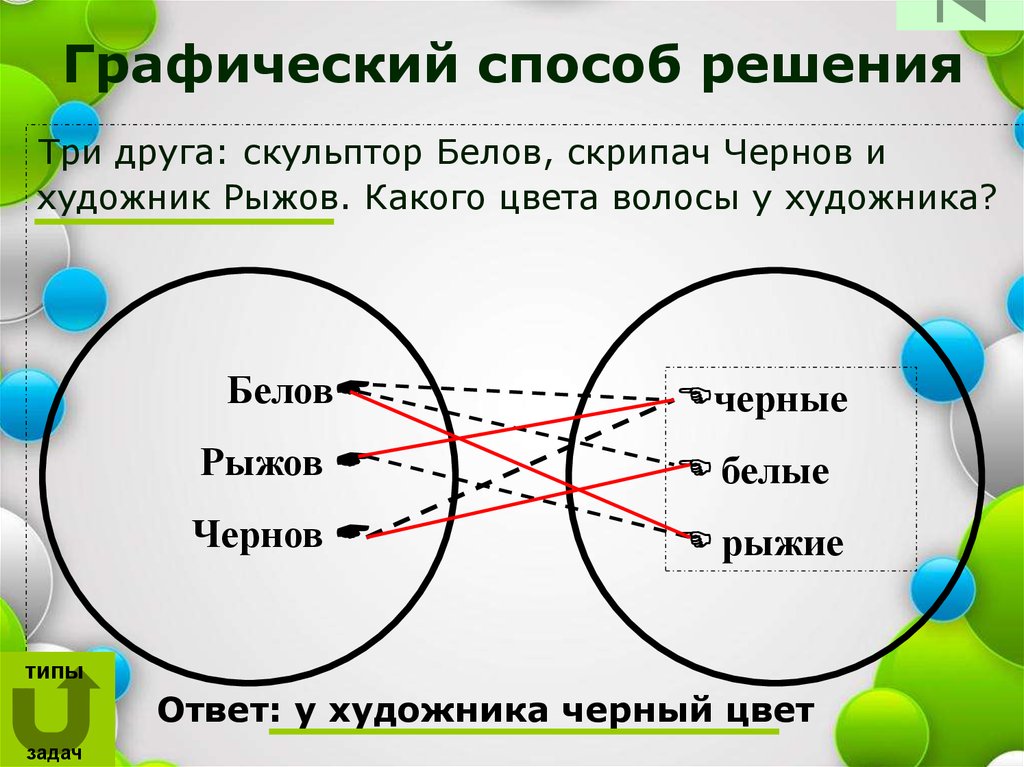
19. Графический способ решения
Три друга: скульптор Белов, скрипач Чернов ихудожник Рыжов. Какого цвета волосы у художника?
Белов
черные
Рыжов
белые
Чернов
рыжие
типы
Ответ: у художника черный цвет
задач
20. Упорядочим множество
В очереди за билетами в кино стоят:Юра, Миша, Володя, Саша и Олег.
Известно, что:
1.Юра купит билет раньше, чем Миша,
но позже Олега.
2.Володя и Олег не стоят рядом.
3.Саша не находится рядом ни с
Олегом, ни с Юрой, ни с Володей.
Кто за кем стоит?
21. Упорядочим множество
Известно, что:1.Юра купит билет раньше, чем Миша, но позже Олега.
Олег
Юра
Миша
2. Володя и Олег не стоят рядом.
3. Саша не находится рядом ни с Олегом, ни с Юрой,
ни с Володей.
типы
задач
Олег
Юра
Олег
Юра
Володя
Миша
Саша
Миша
Саша
22. Графический способ решения (построение графа в виде дерева)
F A&Bконъюнкция
F A+B
дизъюнкция
B
A
A
B
23. Построение логических выражений в виде дерева
F A&(B+С)С
B
A
F (A+В)&(B+С)
B
С
С
B
A
B
24. Решение задач
Задача 1. В соревнованиях по информатике напервенство колледжа участвуют Аня, Валя, Тамара и
Даша. Болельщики высказали предположения о
возможных победителях:
1) Аня будет второй, Даша – четвертой
2) второй будет Тома, Даша – третьей
3) первой будет Тома, Валя – второй
По окончании соревнований оказалось, что
в
каждом
предположении
только
одно
из
высказываний истинно, другое - ложно. Какое место
на соревнованиях заняла каждая из девушек, если все
они оказались на разных местах?
25. Решение задач
Запишем каждое высказывание в буквенномвиде:
1) Аня будет второй, Даша – четвертой
2) второй будет Тома, Даша – третьей
3) первой будет Тома, Валя – второй
Учтем, что в каждом предположении только одно из
высказываний истинно, другое - ложно.
A2 Д 4 или А2 Д 4
Т 2 Д 3 или Т 2 Д 3
Т1 В2 или Т1 В2
26. Решение задач
РешениеДля решения данной задачи составим систему
уравнений
A2 Д 4 А2 Д 4 1
Т 2 Д 3 Т 2 Д 3 1
Т1 В2 Т1 В2 1
Поскольку между строками матрицы стоит
операция конъюнкция каждое уравнение будет
вырастать из предыдущего
27.
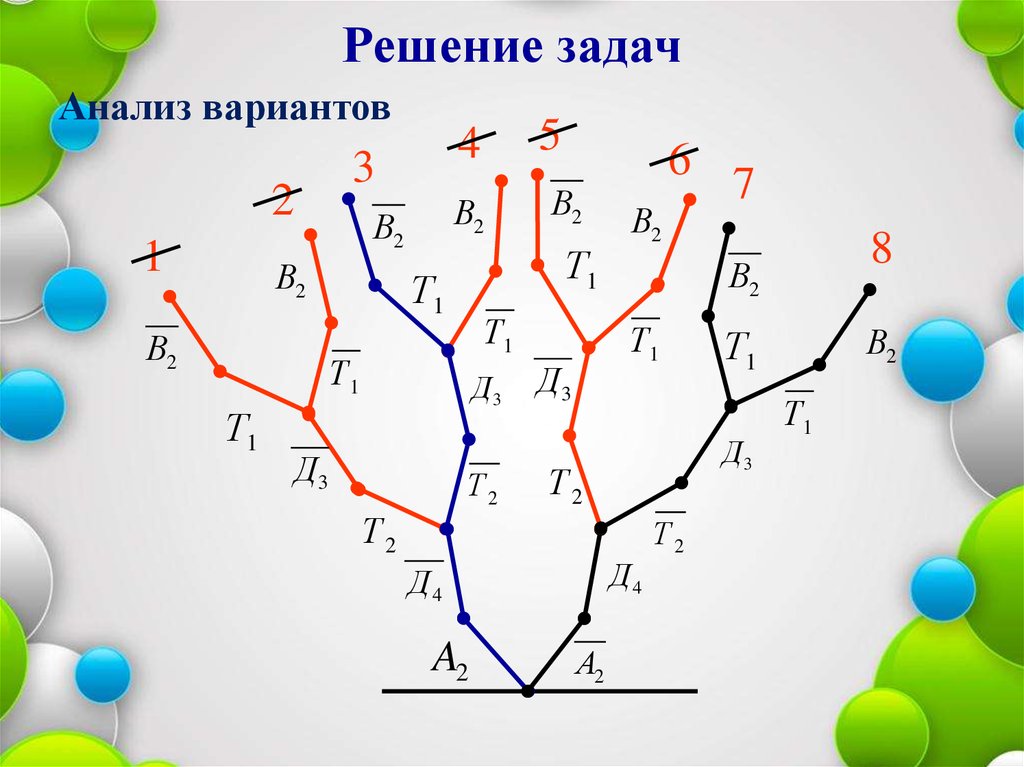
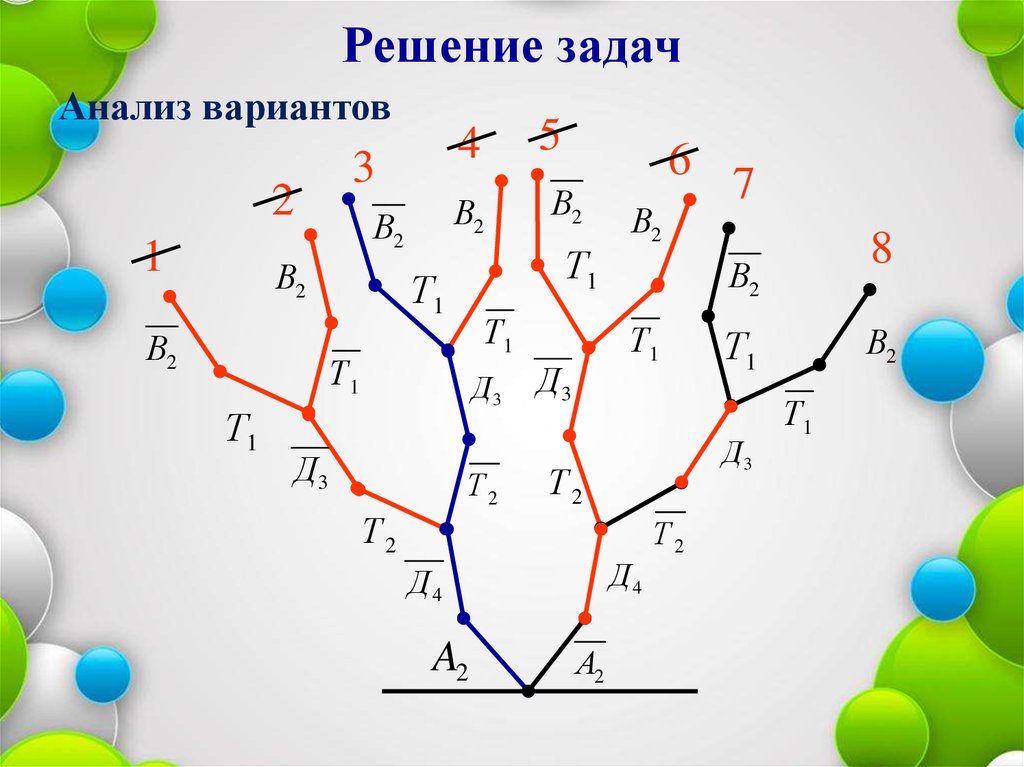
Решение задачПостроение дерева.
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
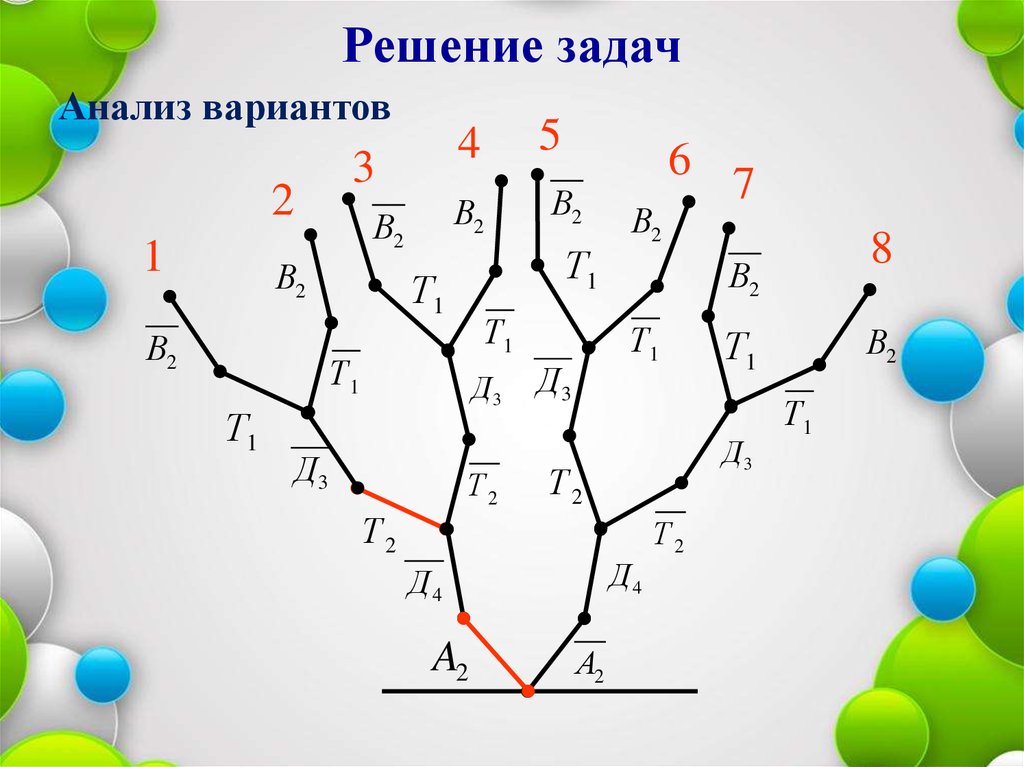
28.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
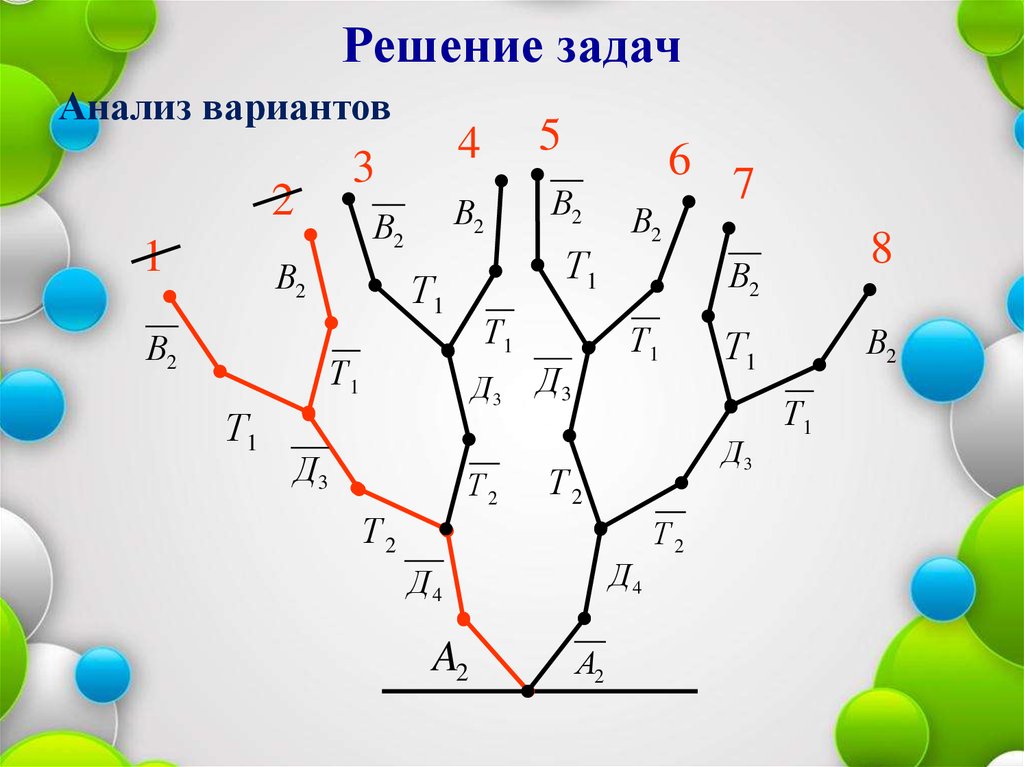
29.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
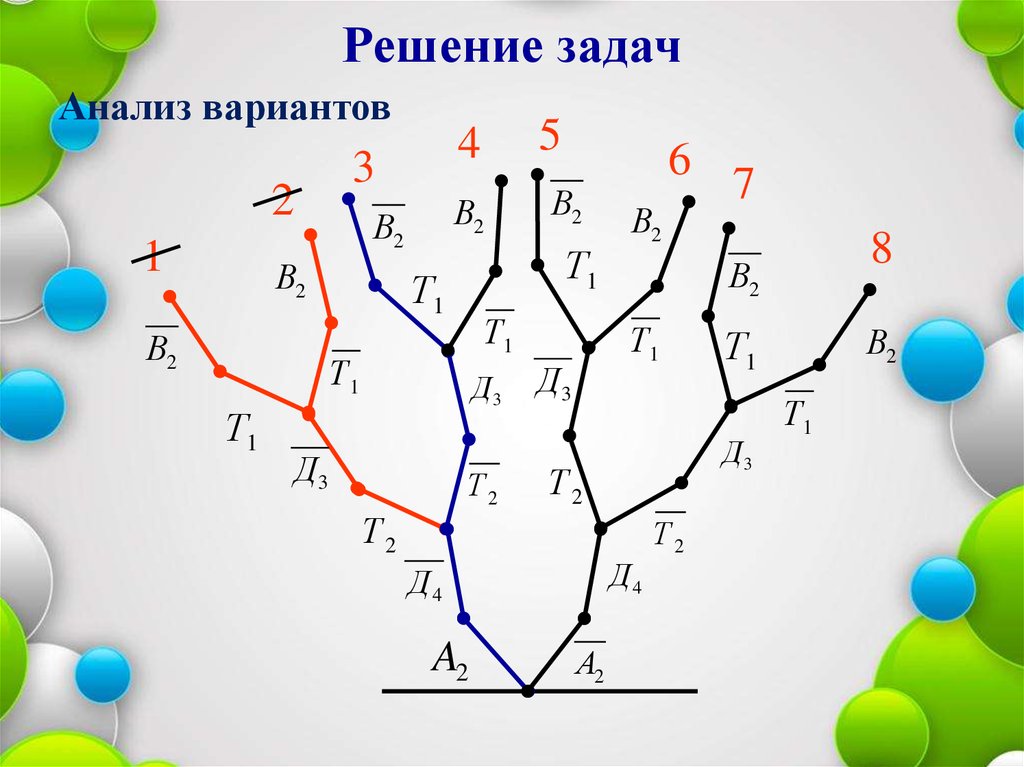
30.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
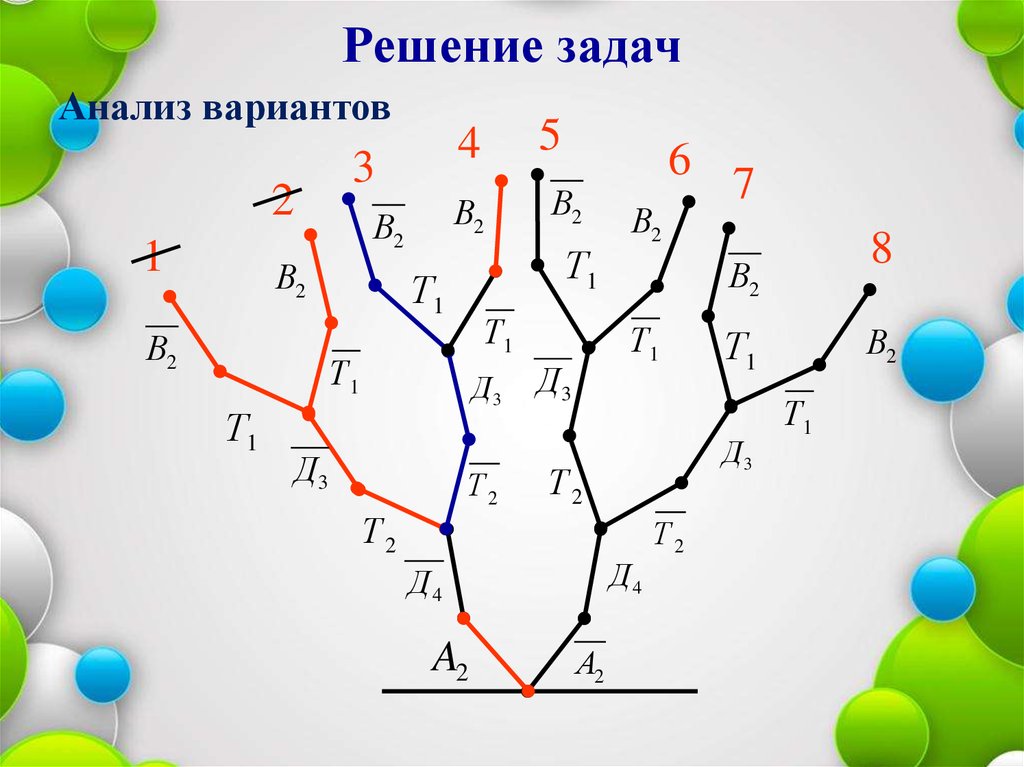
31.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
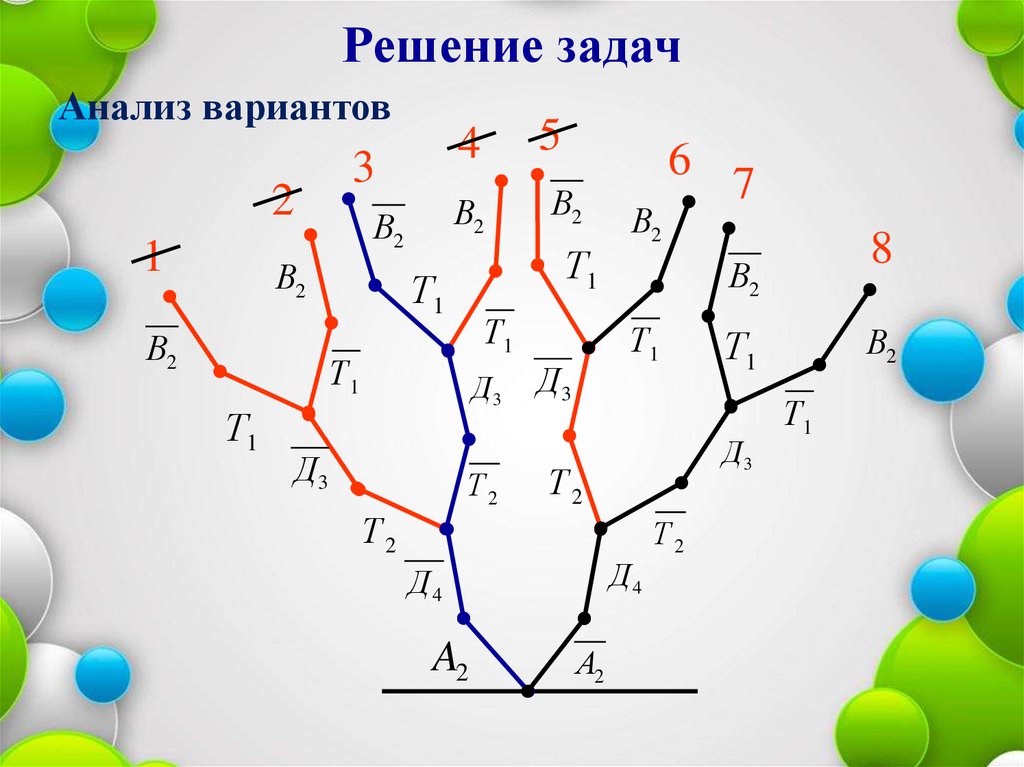
32.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
33.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
34.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
35.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
36.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
37.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
Т2
Т2
Д4
A2
А2
В2
Т1
Д3
Т2
Д4
8
В2
Т1
Д3
7
Т1
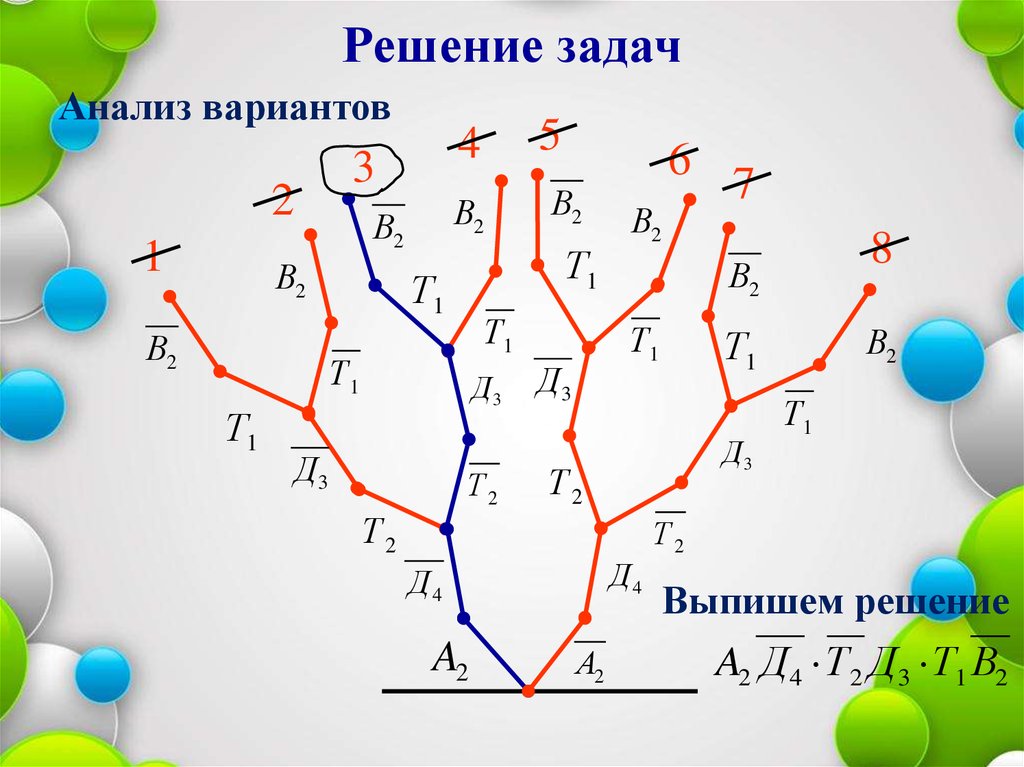
38.
Решение задачАнализ вариантов
3
2
1
В2
В2
В2
В2
Т1
Т1
Д3
Д3
В2
Т1
Т1
Т1
5
4
Т2
6
В2
8
В2
Т1
Д3
7
Д3
Т2
Т2
В2
Т1
Т1
Т2
Д4
Д4
A2
А2
Выпишем решение
A2 Д 4 Т 2 Д3 Т1 В2
39.
Решение задачОтвет:
1 место – Тамара
2 место – Аня
3 место – Даша
4 место – Валя
A2 Д 4 Т 2 Д3 Т1 В2
40.
41.
42.
типызадач
43.
Одна задача - три способа решения« Кто виноват?»
По обвинению в ограблении перед судом предстали три
человека – Иванов, Петров и Сидоров. Установлено
следующее:
1. Если или Иванов невиновен, то Сидоров невиновен.
2. Если Иванов невиновен, то Сидоров невиновен.
Установить, виновен ли Иванов.
Способы решения:
1. средствами алгебры логики (упрощение логического
выражения) ;
2. средствами алгебры логики (таблица истинности);
3. решение задачи на языке Паскаль.
44.
Задача «Кто виноват?»Введем простые высказывания:
I – «Иванов виновен», P – «Петров виновен», C – «Сидоров виновен».
Составим высказывания, выражающие условия задачи
1. I P C I P C I P C
2. I C I C
Умножим (1) на (2), получим:
(I P C) (I C) I P I I P C C I C C
I P I P C C I I P (1 C ) C I
I P C I I (P C) 1
I (P C) 1
Проведем анализ полученного выражения.
Произведение равно 1, если каждый из
сомножителей равен 1. Тогда I = 1, Иванов виновен.
Ответ: Иванов виновен
45.
Задача «Кто виноват?»Составим таблицу истинности
I P C P C I P
I P C
I C
(I P C) (I C)
0 0 0 1 1
0
0
1
0
0 0 1 1 0
0
1
0
0
0 1 0 0 1
0
0
1
0
0 1 1 0 0
0
1
0
0
1 0 0 1 1
1
1
1
1
1 0 1 1 0
1
1
1
1
1 1 0 0 1
0
0
1
0
1 1 1 0 0
0
1
1
1
Ответ: Иванов виноват
46.
Задача «Кто виноват?»I P C I P C I P C
Введем простые высказывания:
I – «Иванов виновен», P – «Петров виновен», C – «Сидоров
виновен».
Составим высказывания, выражающие условия задачи
1.
2.
I C I C
47.
Задача «Кто виноват?»48.
Алеша, Боря и Гриша нашли в земле сосуд.Каждый из них высказал по два
предположения.
Алеша: «Это сосуд греческий, V века».
Боря: «Это сосуд финикийский, III века».
Гриша : «Это сосуд не греческий, IV века».
Учитель истории сказал ребятам, что
каждый из них прав только в одном из двух
своих предположений.
Где и в каком веке был изготовлен сосуд?
49. Решение задачи
Введем обозначения простых высказываний:F - «это сосуд финикийский»,
G - «сосуд греческий»,
V3 - «сосуд изготовлен в III веке»,
V4 - «сосуд изготовлен в IV веке»,
V5 - «сосуд изготовлен в V веке».
50. Средствами алгебры логики
•Изучается условие задачи.•Вводится система обозначений для
логических высказываний.
•Конструируется логическая формула.
•Определяются значения истинности этой
логической формулы.
•Из полученных значений истинности
формулы определяются значения
истинности введенных логических
высказываний, на основании которых
делается заключение о решении.
51.
Виновник ночного дорожно-транспортногопроисшествия скрылся с места аварии.
Первый из опрошенных свидетелей сказал
работникам ГИБДД, что это были «Жигули»,
первая цифра номера машины – единица.
Второй свидетель сказал, что машина была
марки «Москвич», а номер начинался с
семерки.
Третий свидетель заявил, что машина была
иностранная, номер начинался не с единицы.
При дальнейшем расследовании выяснилось,
что каждый из свидетелей правильно указал
либо только марку машины, либо только
первую цифру номера. Какой марки была
машина и с какой цифры начинался номер?
52.
Ж - это «Жигули».М - это «Москвич».
И - это иностранная машина.
Е - номер машины начинается с
единицы.
С - номер машины начинается с
семерки.
53.
• 1: «Жигули», первая цифра номера машины– единица.
Ж Е
• 2: «Москвич», номер начинался с семерки.
М С
• 3: Иностранная, номер начинался не с
единицы.
И Е
54.
• Каждый из свидетелей правильно указаллибо только марку машины, либо только
первую цифру номера.
Ж Е Ж Е
М С М С
И Е И Е
( Ж Е Ж Е ) (М С М С )
(И Е И Е) 1
55.
( Ж Е Ж Е ) (М С М С )(И Е И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
56.
( Ж Е Ж Е ) (М С М С )(И Е И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
57.
Ж М 0; Ж И 0; М И 0; E C 0закон противоречия А А 0
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
( Ж Е М С И Е) ( Ж Е М С И Е )
0 0 0 (Ж Е М С И ) 0 0 0 0
Ж Е М С И
по закону исключения констант А 0 А
58.
Ж Е М С И 1только при Ж 1, M 0, И 0, Е 0, С 1.
• Машина марки «Жигули», номер
которой начинался с цифры семь.
59. Запишем формулы высказываний ребят
Каждый прав только в одном из двух своих предположений.Алеша: «Это сосуд греческий, V века».
G V 5 G V 5 1
Боря: «Это сосуд финикийский, III века».
F V 3 F V 3 1
Гриша : «Это сосуд не греческий, IV века».
G V 4 G V 4 1
То, что сосуд не может быть одновременно изготовлен в
двух государствах или в двух веках (невозможные
события), зададим формулами:
G F 0
V 3 V 5 0
V 4 V 5 0
V 3 V 5 1
V 4 V 5 1
V 3 V 4 0
V 3 V 4 1
G F 1
60. Решение задачи в ЭТ Excel
Высказываний в задаче пятьТаблица истинности содержит 32 строки!!!
25 = 32
По составленным логическим выражениям
составим таблицу истинности в ЭТ Excel
G V 5 G V 5 1
F V 3 F V 3 1 G V 4 G V 4 1
G F 0
V 3 V 5 0
V 4 V 5 0
V 3 V 5 1
V 4 V 5 1
V 3 V 4 0
V 3 V 4 1
G F 1
61.
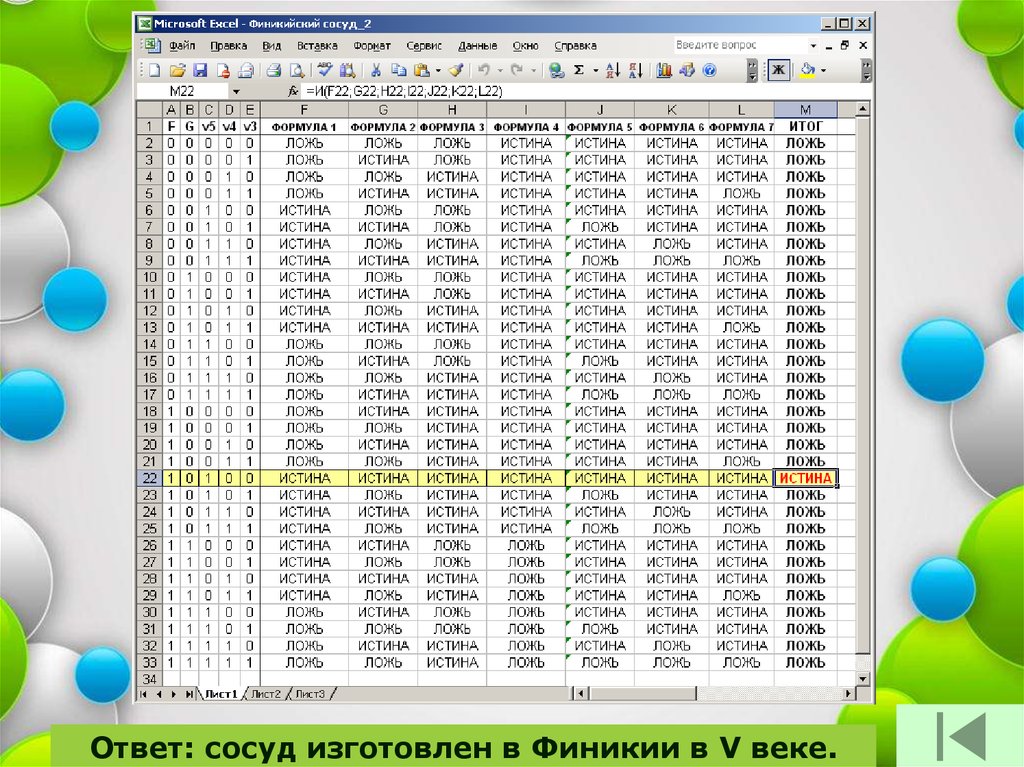
Ввести формулы в ячейки:1. F2 = ИЛИ(И(В2;НЕ(С2));И(НЕ(В2);С2)),
2. G2 = ИЛИ(И(A2;НЕ(E2));И(НЕ(A2);E2)),
3. H2 = ИЛИ(И(НЕ(B2));(НЕ(D2);E2));И(В2;D2)),
4. I2 = НЕ(И(A2;B2)),
5. J2 = НЕ(И(С2;Е2)),
6. K2 = НЕ(И(С2;D2)),
7. L2 = НЕ(И(E2;D2)),
8. M2 = И(F2;G2;H2;I2;J2;K2;L2).
62.
Ответ: сосуд изготовлен в Финикии в V веке.63. Табличный способ решения логических задач
64.
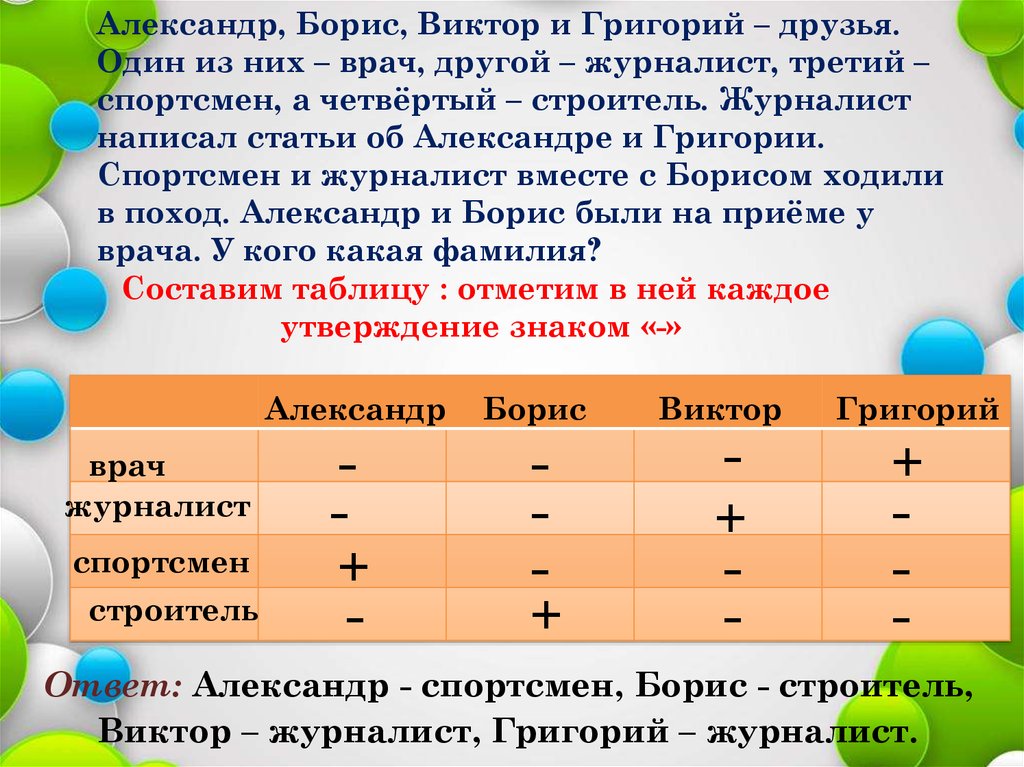
Александр, Борис, Виктор и Григорий – друзья.Один из них – врач, другой – журналист, третий –
спортсмен, а четвёртый – строитель. Журналист
написал статьи об Александре и Григории.
Спортсмен и журналист вместе с Борисом ходили
в поход. Александр и Борис были на приёме у
врача. У кого какая фамилия?
Составим таблицу : отметим в ней каждое
утверждение знаком «-»
Александр
врач
журналист
спортсмен
строитель
+
-
Борис
+
Виктор
+
-
Григорий
+
-
Ответ: Александр - спортсмен, Борис - строитель,
Виктор – журналист, Григорий – журналист.
65.
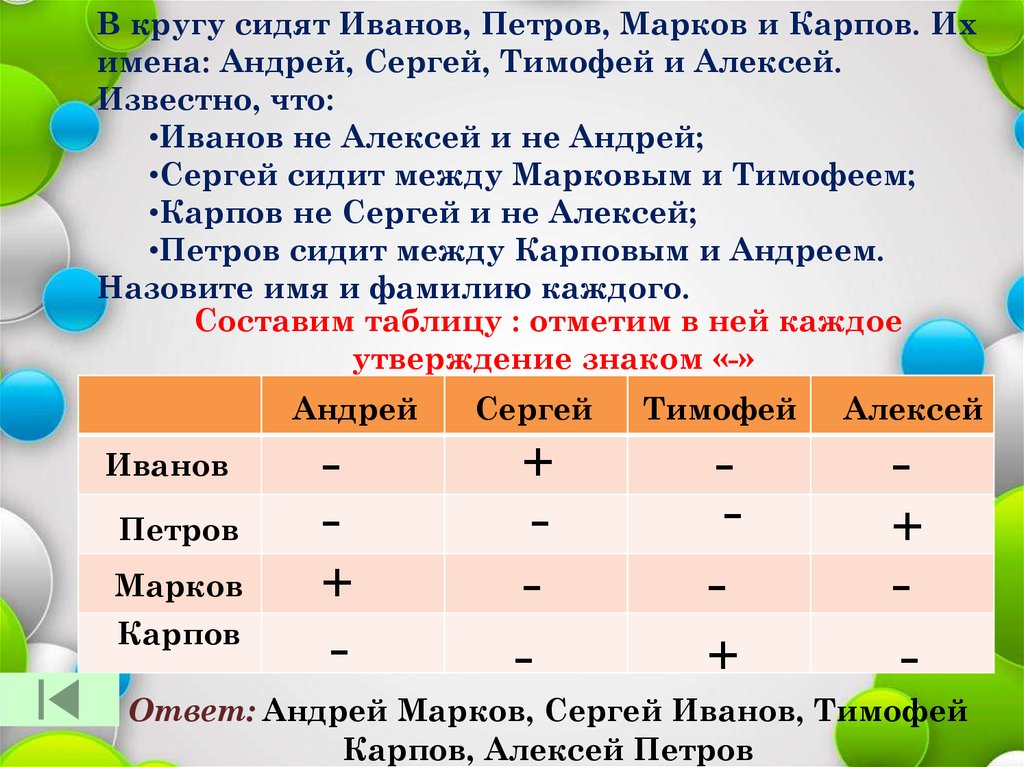
В кругу сидят Иванов, Петров, Марков и Карпов. Ихимена: Андрей, Сергей, Тимофей и Алексей.
Известно, что:
•Иванов не Алексей и не Андрей;
•Сергей сидит между Марковым и Тимофеем;
•Карпов не Сергей и не Алексей;
•Петров сидит между Карповым и Андреем.
Назовите имя и фамилию каждого.
Составим таблицу : отметим в ней каждое
утверждение знаком «-»
Андрей
Иванов
Петров
Марков
Карпов
+
-
Сергей
Тимофей
Алексей
+
-
+
+
-
Ответ: Андрей Марков, Сергей Иванов, Тимофей
Карпов, Алексей Петров
66. Решение логических задач с помощью кругов Эйлера
67.
Все мои подруги выращивают в своих квартирах какиенибудь растения. Шестеро из них разводят лилии, апятеро — фиалки.
И только у двоих есть и лилии и фиалки.
Угадайте, сколько у меня подруг?
Всего 4+2+3=9
68.
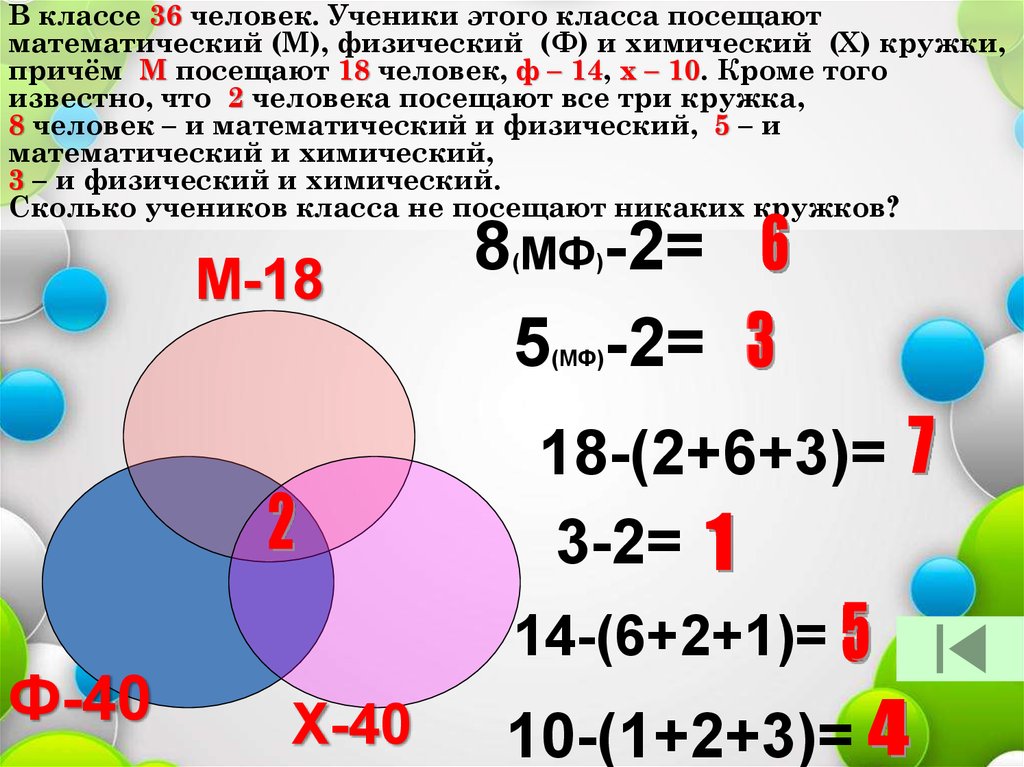
В классе 36 человек. Ученики этого класса посещаютматематический (М), физический (Ф) и химический (Х) кружки,
причём М посещают 18 человек, ф – 14, х – 10. Кроме того
известно, что 2 человека посещают все три кружка,
8 человек – и математический и физический, 5 – и
математический и химический,
3 – и физический и химический.
Сколько учеников класса не посещают никаких кружков?
М-18
8 МФ -2=
5 -2=
(
)
(МФ)
18-(2+6+3)=
3-2=
Ф-40
14-(6+2+1)=
Х-40
10-(1+2+3)=
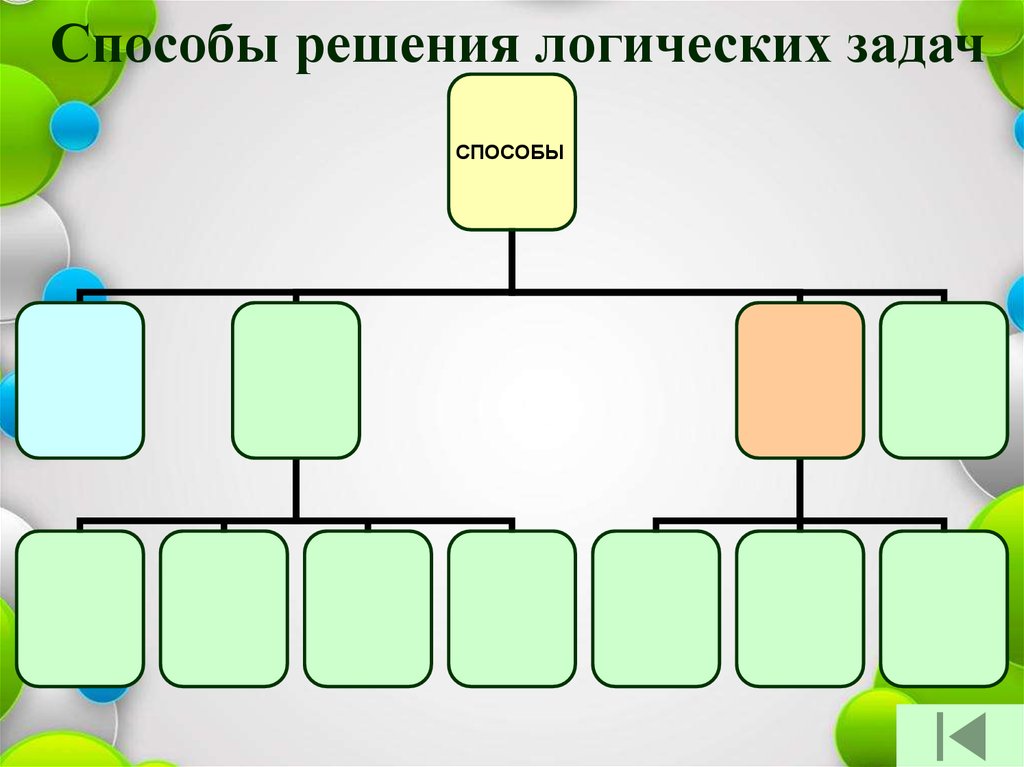
69.
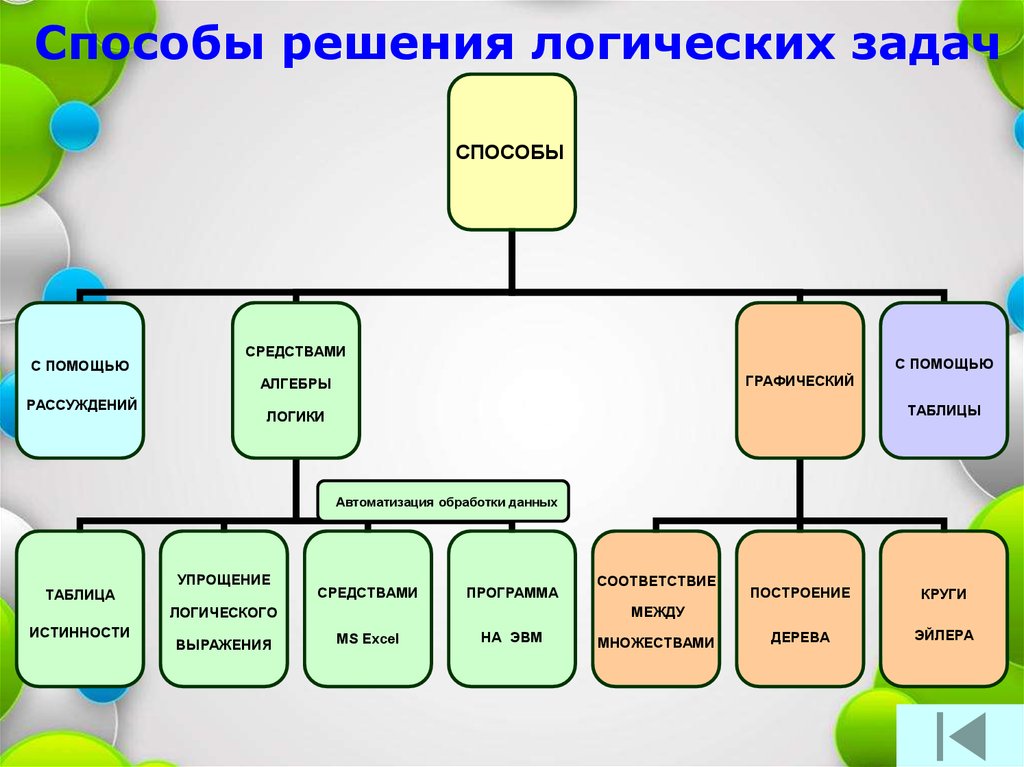
Способы решения логических задачСПОСОБЫ
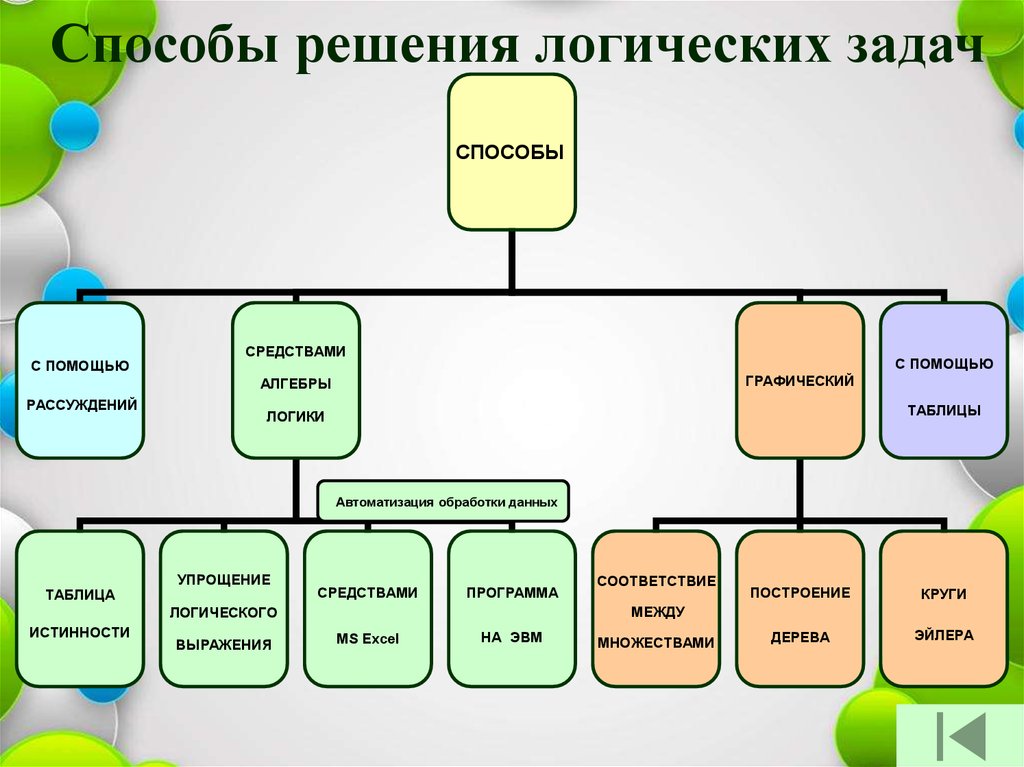
70.
Способы решения логических задачСПОСОБЫ
С ПОМОЩЬЮ
СРЕДСТВАМИ
С ПОМОЩЬЮ
ГРАФИЧЕСКИЙ
АЛГЕБРЫ
РАССУЖДЕНИЙ
ТАБЛИЦЫ
ЛОГИКИ
Автоматизация обработки данных
ТАБЛИЦА
УПРОЩЕНИЕ
СРЕДСТВАМИ
ПРОГРАММА
ВЫРАЖЕНИЯ
ПОСТРОЕНИЕ
КРУГИ
ДЕРЕВА
ЭЙЛЕРА
МЕЖДУ
ЛОГИЧЕСКОГО
ИСТИННОСТИ
СООТВЕТСТВИЕ
MS Excel
НА ЭВМ
МНОЖЕСТВАМИ
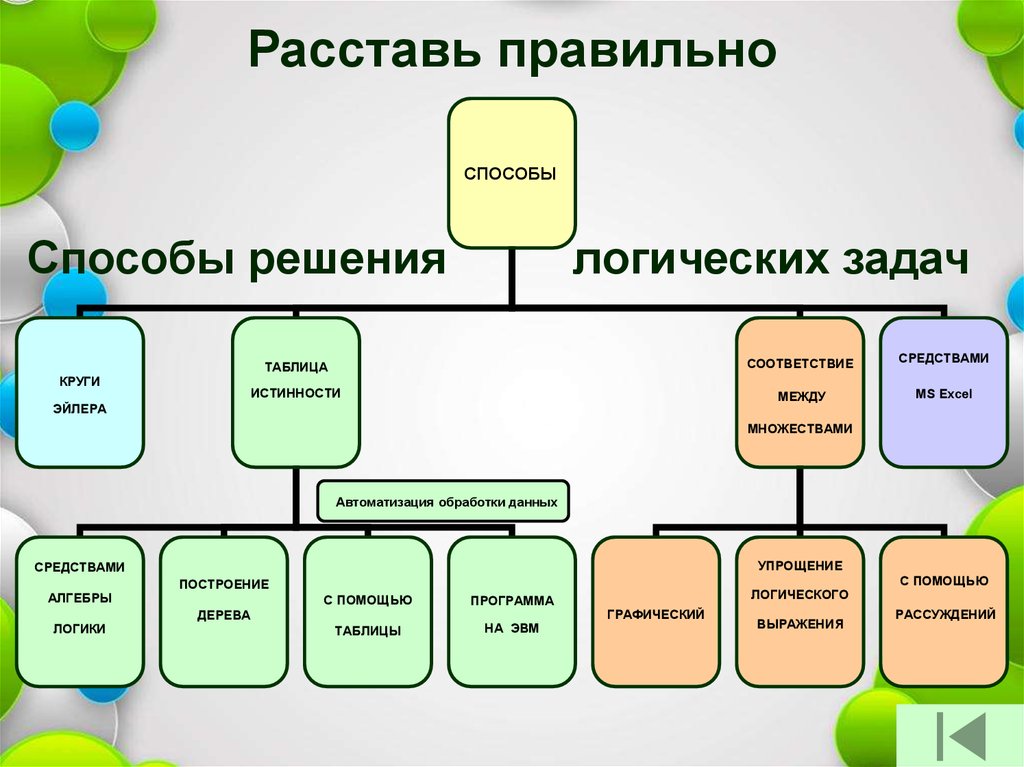
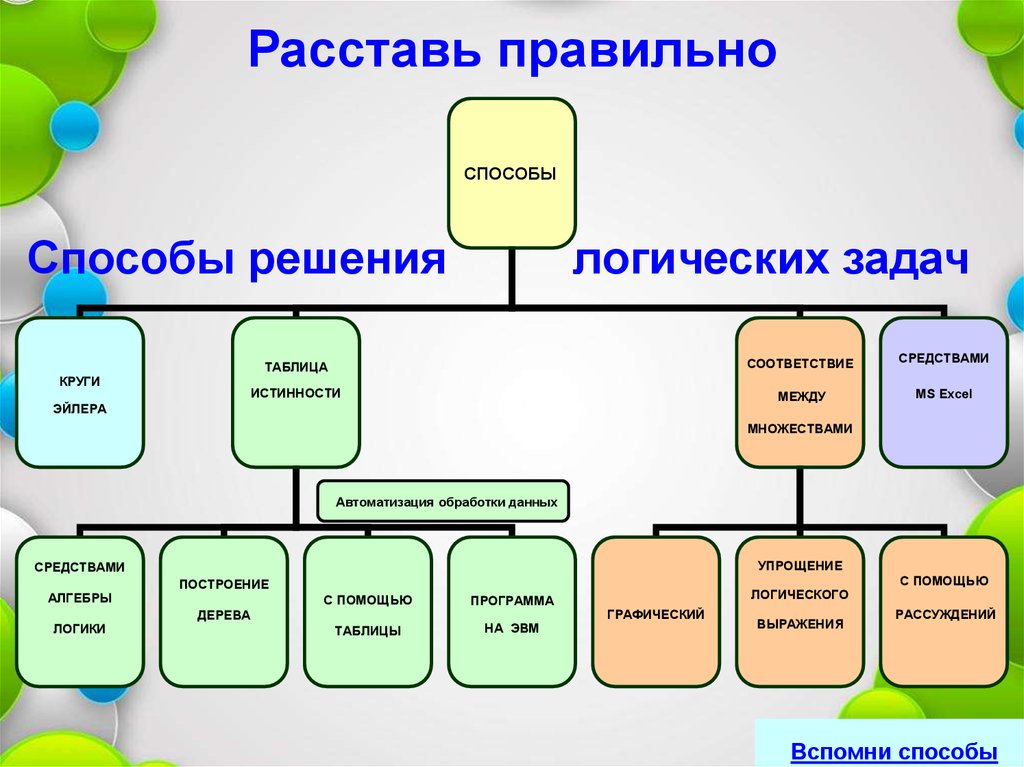
71.
Расставь правильноСПОСОБЫ
Способы решения
КРУГИ
логических задач
ТАБЛИЦА
СООТВЕТСТВИЕ
СРЕДСТВАМИ
ИСТИННОСТИ
МЕЖДУ
MS Excel
ЭЙЛЕРА
МНОЖЕСТВАМИ
Автоматизация обработки данных
УПРОЩЕНИЕ
СРЕДСТВАМИ
АЛГЕБРЫ
ЛОГИКИ
ПОСТРОЕНИЕ
С ПОМОЩЬЮ
ПРОГРАММА
ТАБЛИЦЫ
НА ЭВМ
ДЕРЕВА
ЛОГИЧЕСКОГО
ГРАФИЧЕСКИЙ
ВЫРАЖЕНИЯ
С ПОМОЩЬЮ
РАССУЖДЕНИЙ
72. Повторительно – обобщающий урок по теме: Способы решения логических задач
73.
«Если у двух человек есть по одномуяблоку и они обмениваются ими, у каждого из
них окажется по одному яблоку. Но если у
двух человек есть по одной идее и они
обмениваются ими, у каждого будет по две
идеи»
Б. Шоу
Цель урока:
повторить способы решения логических задач;
сравнить их;
углубить понимание обобщенной схемы
классификации способов решения;
закрепить навыки выбора способа решения .
74. Способы решения логических задач
Тема урока:Способы решения
логических задач
В одном мгновенье видеть вечность,
Огромный мир – в зерне песка….
У. Блейк
75.
1. Какие типы задач мы разбирали?2. Какие новые способы решения логических
задач разобрали, изучая «алгебру логики»?
3. Восстанови схему. Правильно!!!
4. Автоматизированные способы – почему не
выделены в отдельную группу?
5. Каков алгоритм решения задач с помощью
«алгебры логики»?
6. Какой способ ?
7. Разминка_1. Разминка_2. Задачи .
76.
Алгоритм решения задач средствамиалгебры логики:
изучается условие задачи;
вводится система обозначений для логических
высказываний;
конструируется логическая формула,
описывающая логические связи между всеми
высказываниями условия задачи;
определяются значения истинности этой
логической формулы.
77. Разминка
«Если у двух человек есть по одномуяблоку и они обмениваются ими, у
каждого из них окажется по одному
яблоку. Но если у двух человек есть
по одной идее и они обмениваются
ими, у каждого будет по две идеи»
Б. Шоу
Проверь
78. Разминка
«Если ты направился к цели истанешь дорогою останавливаться,
чтобы швырять камнями во всякую
лающую на тебя собаку, то никогда
не дойдешь до цели»
Проверь
Ф.М. Достоевский
79.
Расставь правильноСПОСОБЫ
Способы решения
КРУГИ
логических задач
ТАБЛИЦА
СООТВЕТСТВИЕ
СРЕДСТВАМИ
ИСТИННОСТИ
МЕЖДУ
MS Excel
ЭЙЛЕРА
МНОЖЕСТВАМИ
Автоматизация обработки данных
УПРОЩЕНИЕ
СРЕДСТВАМИ
АЛГЕБРЫ
ЛОГИКИ
ПОСТРОЕНИЕ
С ПОМОЩЬЮ
ПРОГРАММА
ТАБЛИЦЫ
НА ЭВМ
ДЕРЕВА
ЛОГИЧЕСКОГО
ГРАФИЧЕСКИЙ
ВЫРАЖЕНИЯ
С ПОМОЩЬЮ
РАССУЖДЕНИЙ
Вспомни
Вспомни способы
способы
80.
Способы решения логических задачСПОСОБЫ
С ПОМОЩЬЮ
СРЕДСТВАМИ
С ПОМОЩЬЮ
ГРАФИЧЕСКИЙ
АЛГЕБРЫ
РАССУЖДЕНИЙ
ТАБЛИЦЫ
ЛОГИКИ
Автоматизация обработки данных
ТАБЛИЦА
УПРОЩЕНИЕ
СРЕДСТВАМИ
ПРОГРАММА
ВЫРАЖЕНИЯ
ПОСТРОЕНИЕ
КРУГИ
ДЕРЕВА
ЭЙЛЕРА
МЕЖДУ
ЛОГИЧЕСКОГО
ИСТИННОСТИ
СООТВЕТСТВИЕ
MS Excel
НА ЭВМ
МНОЖЕСТВАМИ
81. Какой способ выбрать?
Дорогу осилит идущий, а логику мыслящийОпределите тип задачи
Самая короткая дорога –знакомая. Способ которым
владеешь – лучший!
Главное получить верный результат!
82.
«Если у двух человек есть по одному яблоку и ониобмениваются ими, у каждого из них окажется
по одному яблоку. Но если у двух человек есть
по одной идее и они обмениваются ими, у
каждого будет по две идеи» (Б. Шоу)
А: «У двух человек есть по одному яблоку»;
В: «У двух человек есть по одной идее»;
С: «Люди обменяются имеющимися у них
предметами»;
D: «У двух человек есть по две идеи»;
((A&C) A)&((B&C) D)
83.
«Если ты направился к цели и станешьдорогою останавливаться, чтобы швырять
камнями во всякую лающую на тебя собаку,
то никогда не дойдешь до цели» (Ф.М.
Достоевский)
А: «Ты направился к цели»;
В: «Ты станешь дорогою
останавливаться»;
С: «Ты станешь швырять камнями во
всякую лающую на тебя собаку»;
D: «Ты дойдешь до цели»;
( A & B & C) D
84.
«….по одной капле воды…человек,умеющий мыслить логически, может
сделать вывод о существовании
Атлантического океана или Ниагарского
водопада, даже если он не видел ни того,
ни другого и никогда о них не слыхал…
По ногтям человека, по его рукам, обуви,
сгибу на коленях, по выражению лица и
обшлагам рубашки – по таким мелочам
нетрудно угадать его профессию.
И можно не сомневаться, что все это
вместе взятое, подскажет сведущему
наблюдателю верные выводы»
А. Конан Дойл












































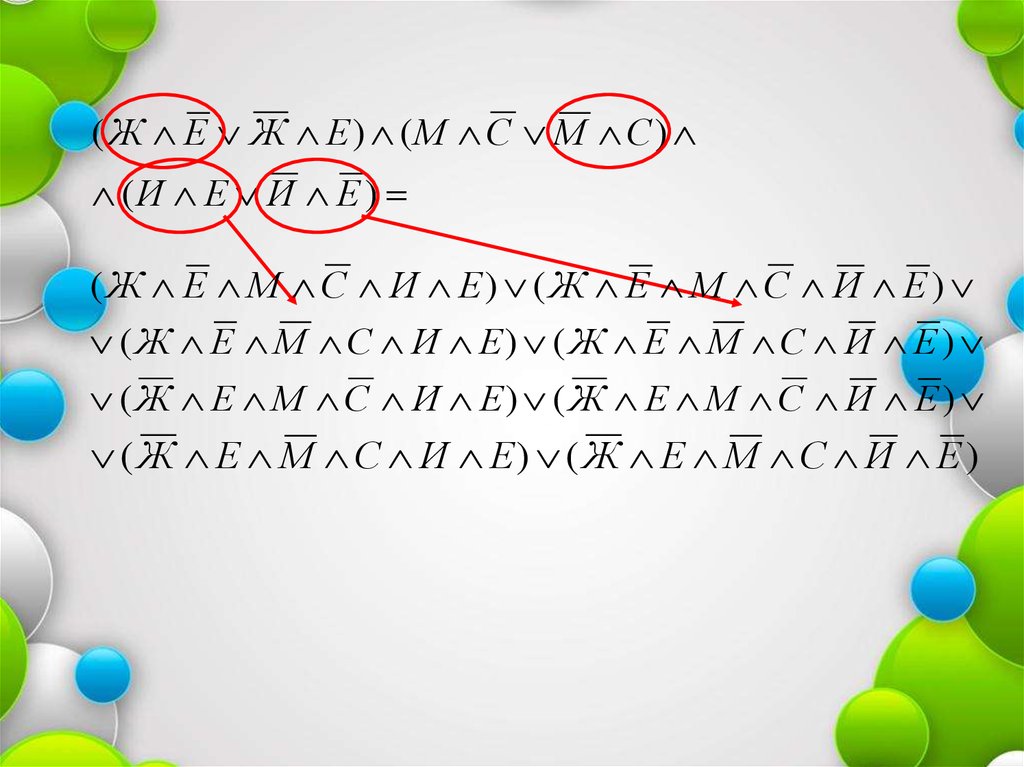



















 Математика
Математика








