1.81M

Категория: $Математика$ Математика

Похожие презентации:

Квадратичная функция, ее график и свойства

Квадратичная функция, ее график. Преобразование графика квадратичной функции

Построение графика квадратичной функции у(х)= ах2 + вх + с

Решение квадратных неравенств. (метод интервалов). 8 класс

Линейная и квадратичная функции и их графики

Построение графиков функций содержащих знак модуля

Квадратичная функция, её свойства и график

Касательная к графику функции

Числовые функции и графики

Квадратичная функция и её график

Общая теория. Графики. Тренажер

1. 2. Общая теория

1. Графиком линейной функции у=кх + b является
прямая. Для построения прямой надо знать 2
точки.
2. Графиком обратной пропорциональности у=к/х
является гипербола. Она не пересекает оси
координат.
3. Графиком квадратичной функции у=ах2+вх +с
является парабола. Чтобы построить параболу,
надо найти вершину параболы х0=- в/(2а),
у0=f(x0). Найдите еще 2-3 точки справа от х0,
постройте еще 3 точки относительно оси
симметрии параболы.

3. Теория к заданиям вида 1.

1. Составьте систему уравнений, чтобы найти общую точку
графиков.
2. Приравняйте правые части уравнений.
3. Квадратное уравнение решайте с помощью
дискриминанта. Помните: что один корень квадратного
уравнения бывает только тогда, когда дискриминант
равен нулю.
4. Найдите параметр, подставьте его значение в формулы и
постройте графики получившихся функций.
Перейти
к заданию 1
к заданию 2
к заданию 3
к заданию 4
к заданию 5
к заданию 6
к заданию 7
к заданию 8

4.

1. Известно, что графики функций
И
имеют ровно одну общую точку. Определите
координаты этой точки. Постройте графики
заданных функций в одной системе координат.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

5.

2. Известно, что графики функций
и
имеют ровно одну общую
точку. Определите координаты этой точки.
Постройте графики заданных функций в одной
системе координат.
Подсказка 1.
Решение.
Подсказка 2 .
Ответ.

6.

3. Известно, что графики функций
и
имеют ровно одну общую
точку. Определите координаты этой точки.
Постройте графики заданных функций в одной
системе координат.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

7.

4. Найдите все значения k, при каждом
из которых прямая
ком функции
имеет с графировно одну
общую точку. Постройте этот график и все
такие прямые.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

8.

5. Найдите все значения k, при каждом
из которых прямая
ком функции
имеет с графировно одну
общую точку. Постройте этот график и все
такие прямые.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

9.

6. При каких отрицательных значениях k пря-
мая
имеет с параболой
ровно одну общую точку?
Найдите координаты этой точки и постройте
данные графики в одной системе координат.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

10.

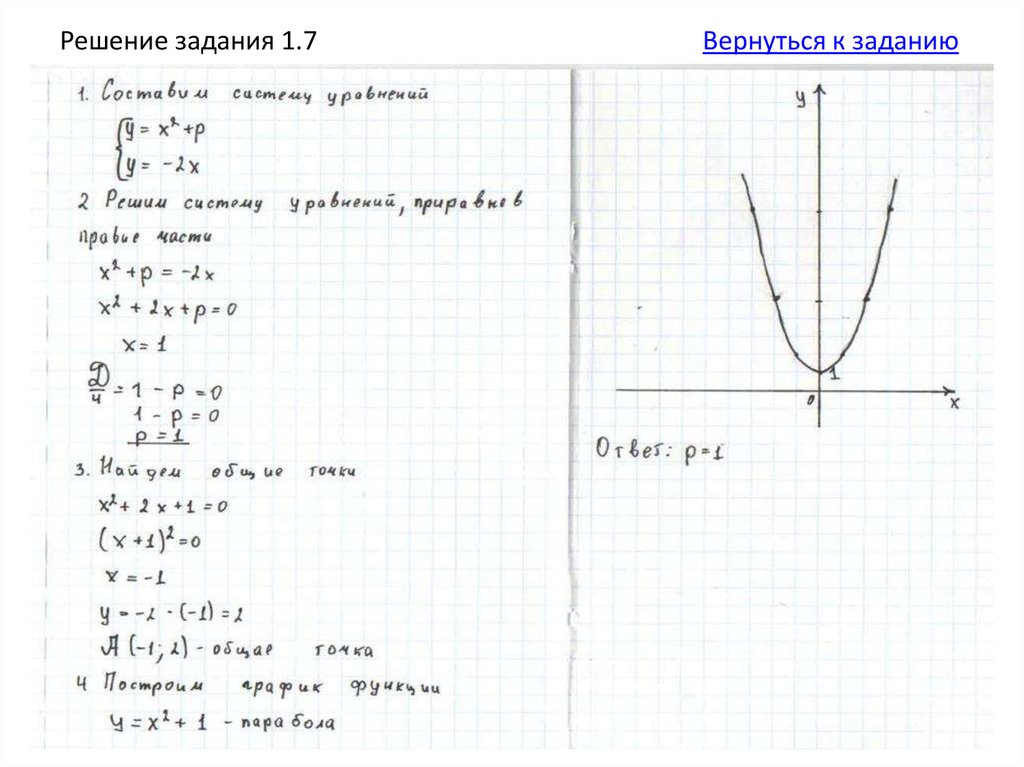
7. Найдите p и постройте график функции
если известно, что прямая
имеет с графиком ровно одну
общую точку.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

11.

8. Прямая y = 2x + b касается окружности
x2 + y2 = 5 в точке с положительной абсциссой.
Определите координаты точки касания.
Подсказка 1.
Подсказка 2.
Решение.
Ответ.

12. Теория к заданиям вида 2.

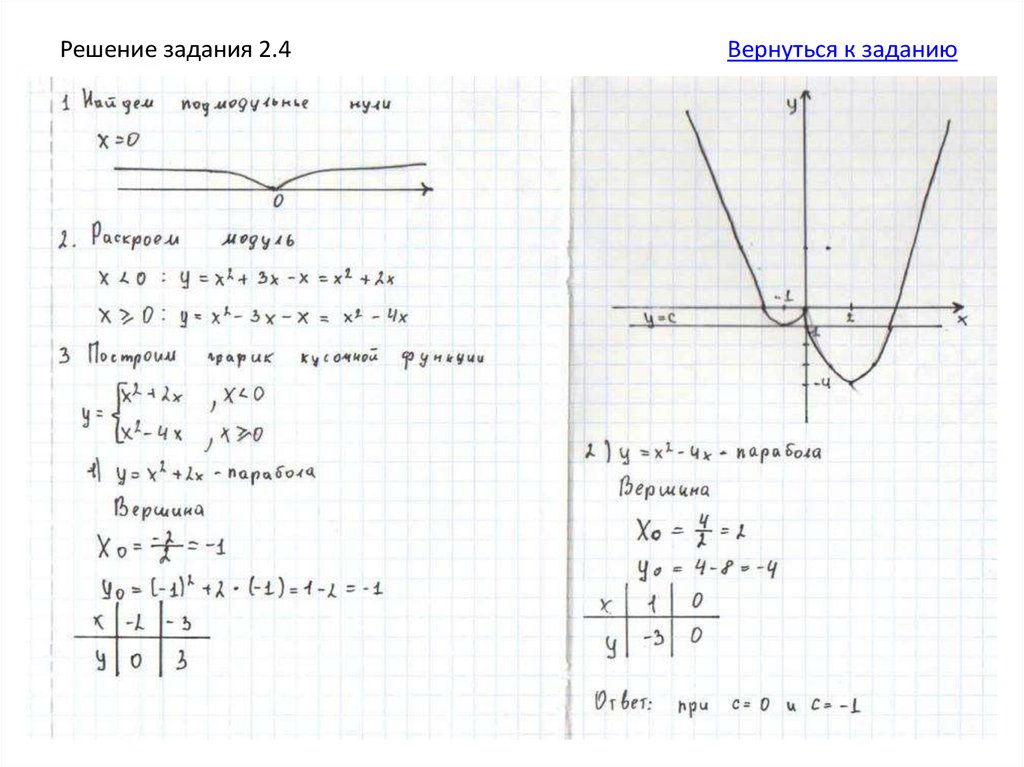
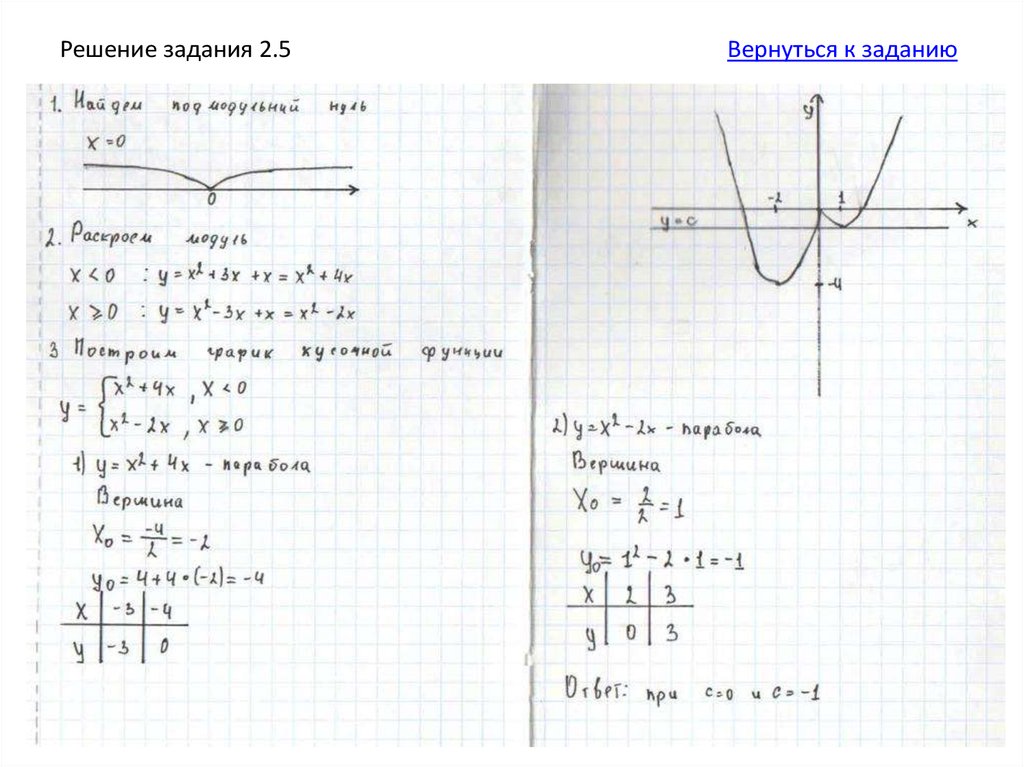
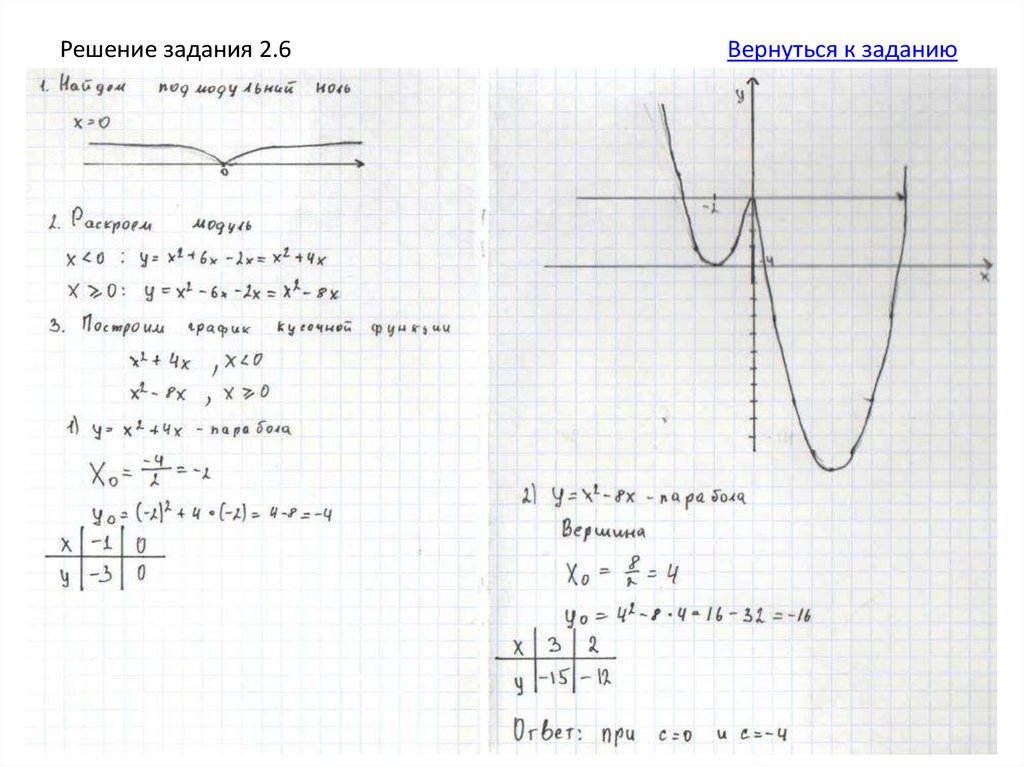
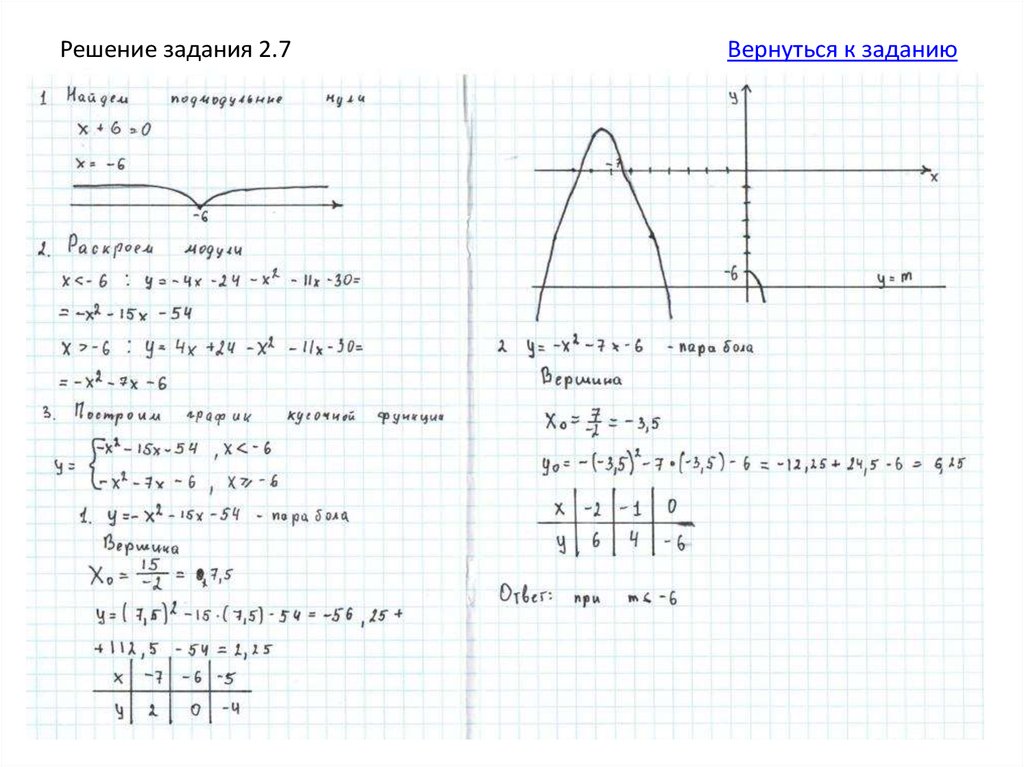
1. Найдите подмодульные нули (контрольные точки),
разбейте прямую на промежутки.
2. Раскройте модули на каждом промежутке.
3. Построите график кусочной функции.
4. Прямая у=в параллельна оси х. Постройте несколько
таких прямых. Запишите ответ.
Перейти
к заданию 1
к заданию 2
к заданию 3
к заданию 4
к заданию 5
к заданию 6
к заданию 7
к заданию 8

13.

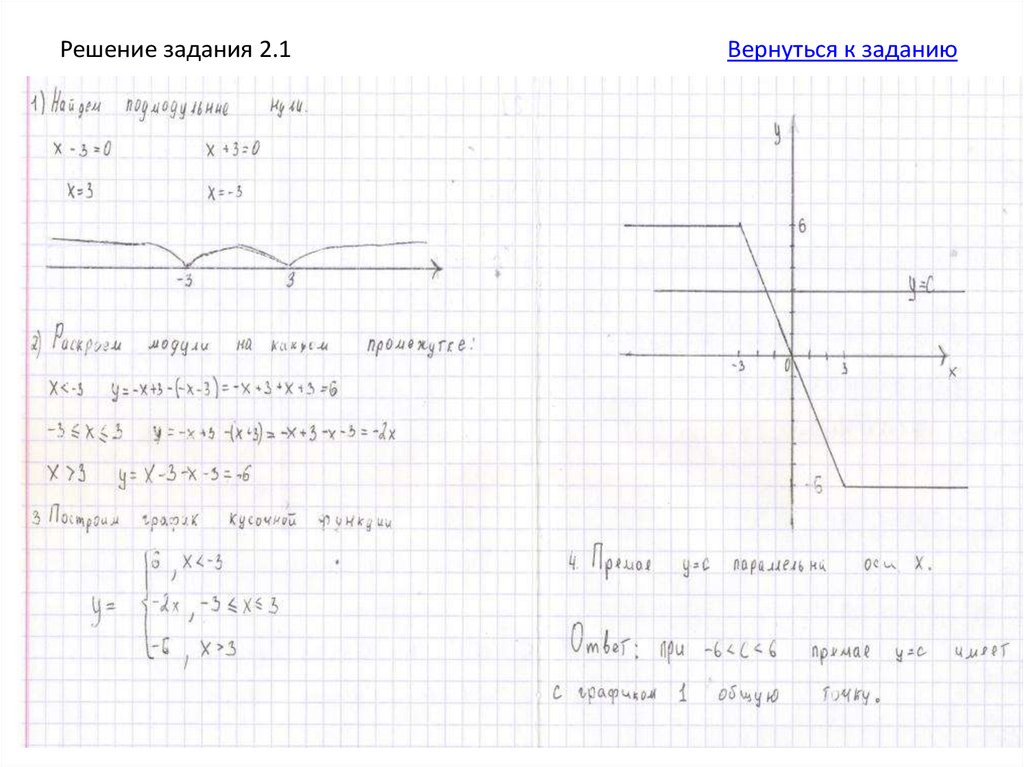
1. Постройте график функции
и определите, при каких значениях с прямая у = с
имеет с графиком ровно одну общую точку.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

14.

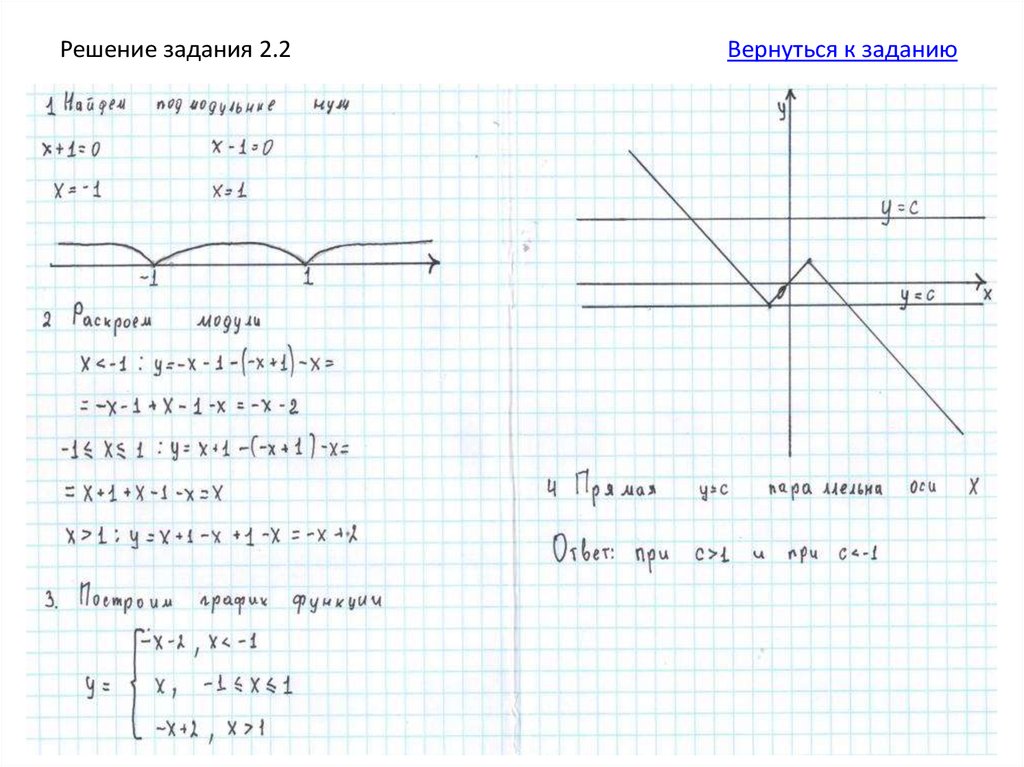
2. Постройте график функции
и определите, при каких значениях с прямая у = с
имеет с графиком ровно одну общую точку.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

15.

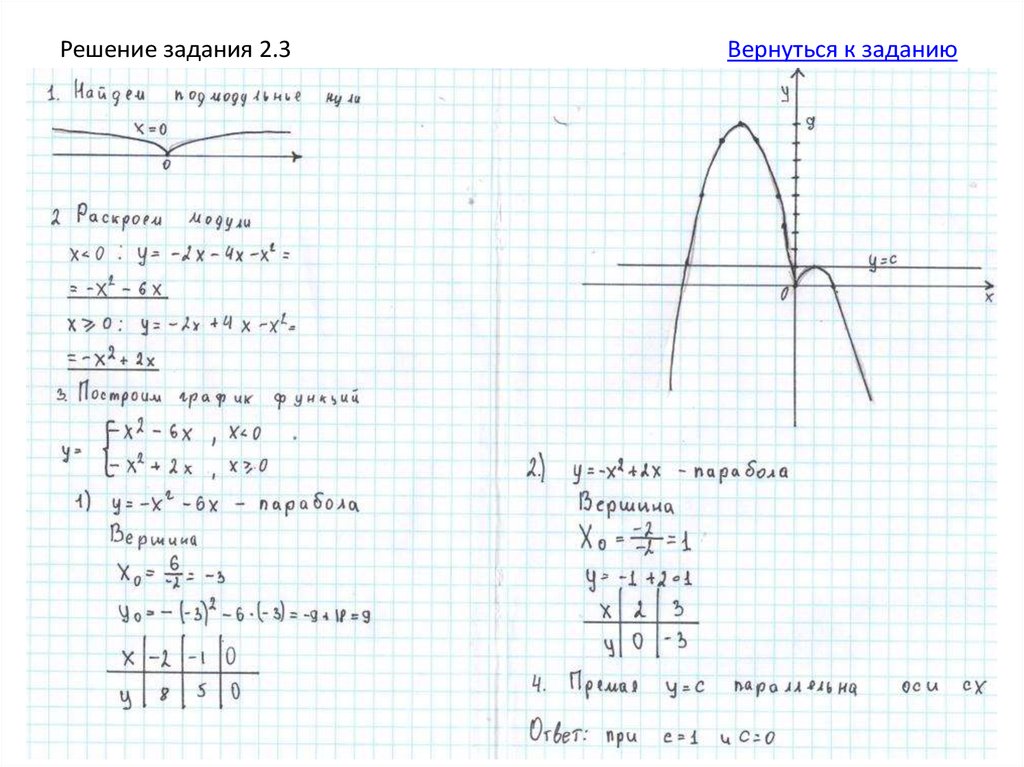
3. Постройте график функции
и определите, при каких значениях с прямая у
= с имеет с графиком ровно три общие
точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

16.

4. Постройте график функции
и определите, при каких значениях с прямая у
= с имеет с графиком ровно три общие
точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

17.

5. Постройте график функции
и определите, при каких значениях с прямая у
= с имеет с графиком ровно три общие
точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

18.

6. Постройте график функции
и определите, при каких значениях с прямая у
= с имеет с графиком ровно три общие
точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

19.

7. Постройте график функции
и определите,
при каких значениях т прямая у = т имеет с
графиком ровно три общие точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

20.

8. Постройте график функции
и определите,
при каких значениях т прямая у = т имеет с
графиком ровно три общие точки.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

21. Теория к заданиям вида 3.

1.
2.
3.
4.
5.
Квадратичная функция имеет вид у=ах2+вх+с.
Составьте систему 3 уравнений, подставив координаты точек.
Решите систему уравнений, найдя значения а, в и с.
Запишите получившуюся формулу квадратичной функции.
Найдите координаты вершины параболы, используя формулы
х0=- в/(2а), у0=f(x). Запишите ответ.
Перейти
к заданию 1
к заданию 2
к заданию 3
к заданию 4
к заданию 5

22.

1. Парабола проходит через точки
A(0; 6), B(6; –6), C(1; 9).
Найдите координаты её вершины.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

23.

2. Парабола проходит через точки
A(0; 4), B(1; 11), C(–5; –1).
Найдите координаты её вершины.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

24.

3. Парабола проходит через точки
A(0; – 6), B(1; – 9), C(6; 6).
Найдите координаты её вершины.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

25.

4. Парабола проходит через точки
K(0; –2), L(4; 6), M(1; 3).
Найдите координаты её вершины.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

26.

5. Парабола проходит через точки
K(0; –5), L(4; 3), M(–3; 10).
Найдите координаты её вершины.
Подсказка 1.
Решение.
Подсказка 2.
Ответ.

27.

28.

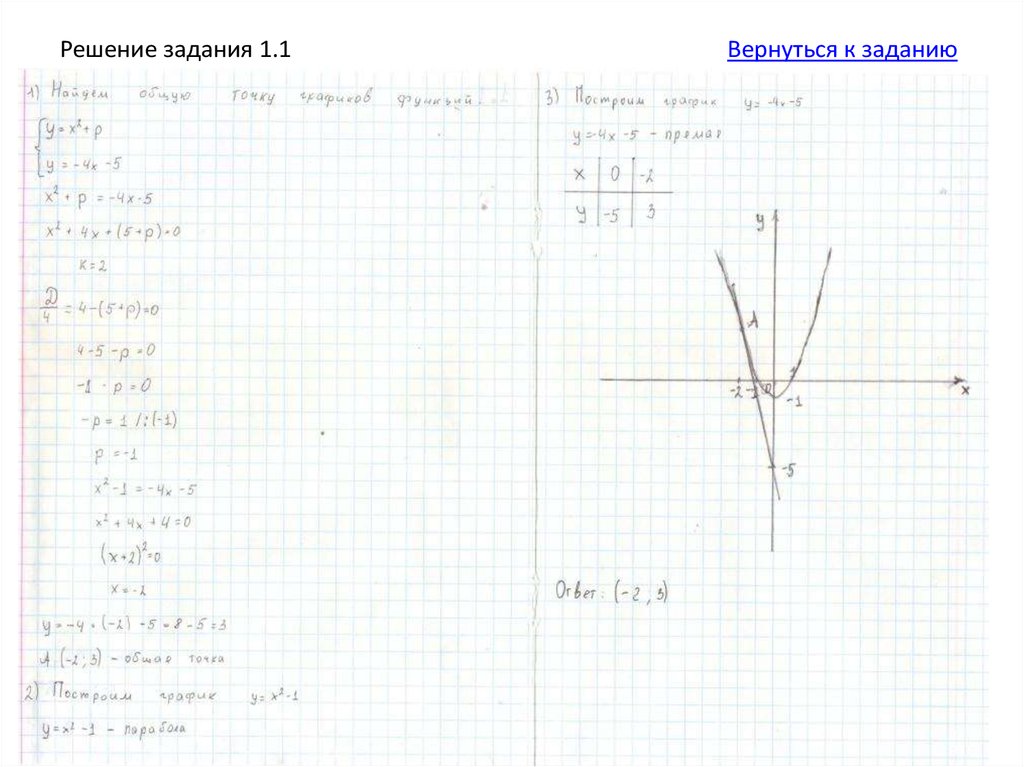
1.Составьте систему уравнений:
у = х2+ р;
у = - 4х – 5.
2. Приравняйте правые части
х2+ р = - 4х – 5.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

29.

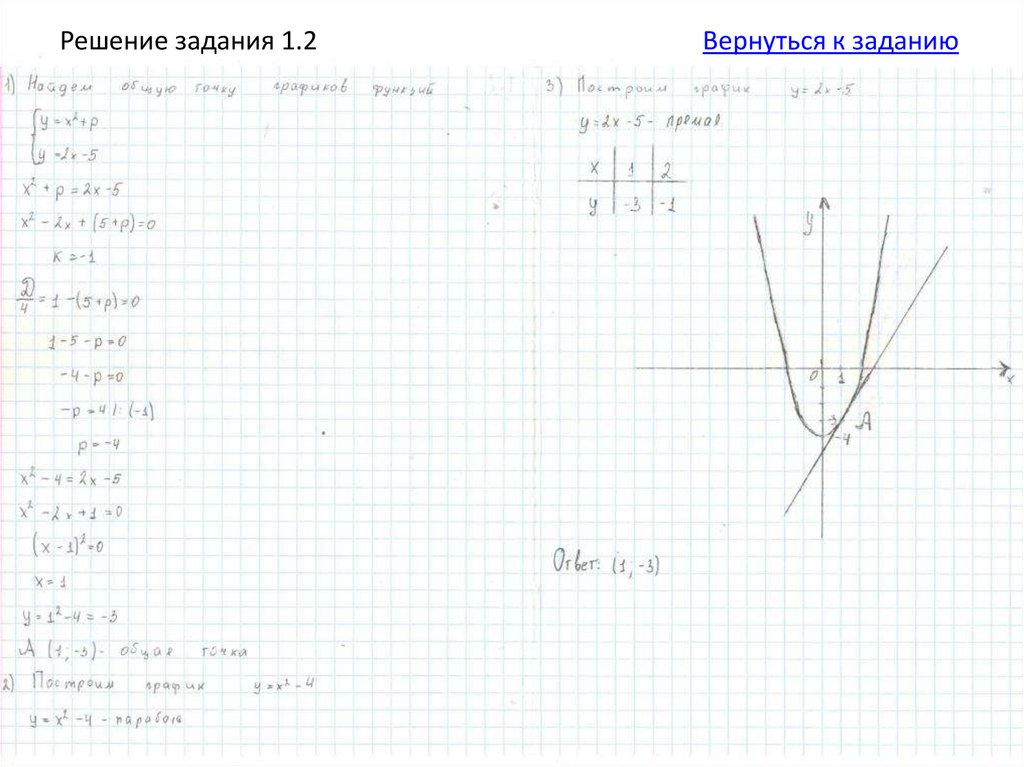
1.Составьте систему уравнений:
у = х2+ р;
у = 2х – 5.
2. Приравняйте правые части
х2+ р = 2х – 5.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

30.

1.Составьте систему уравнений:
у = х2+ р;
у = - 2х – 5.
2. Приравняйте правые части
х2+ р = - 2х – 5.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

31.

1.Составьте систему уравнений:
у = кх;
у = - х2 – 6,25.
2. Приравняйте правые части
кх = - х2 – 6,25.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

32.

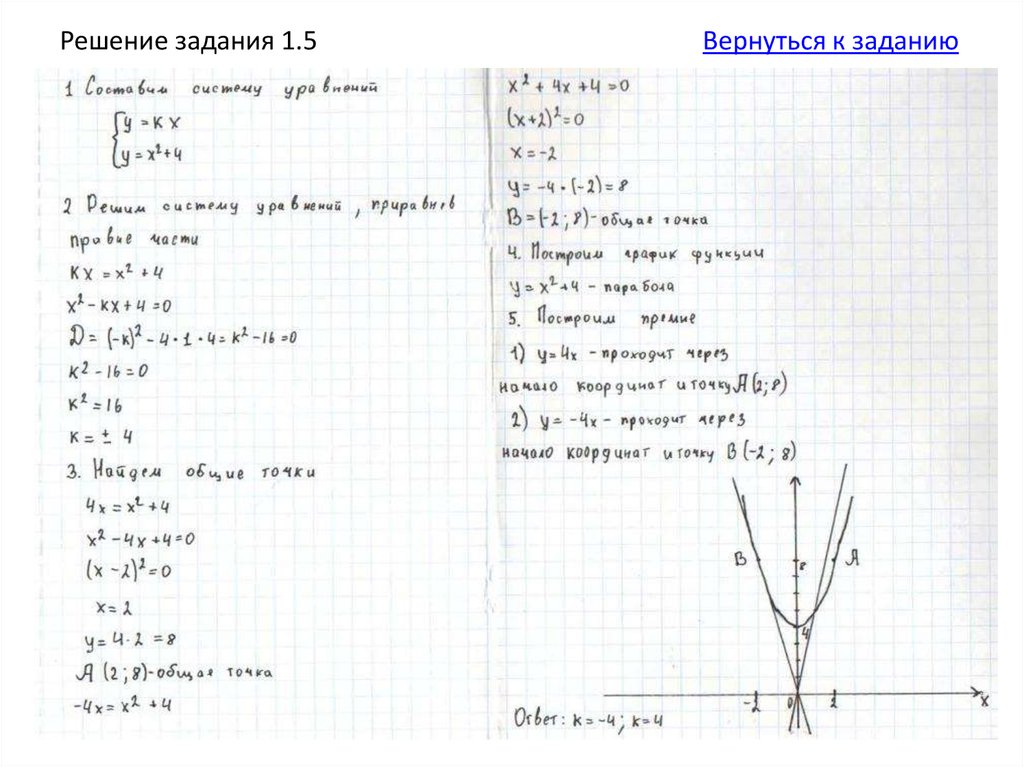
1.Составьте систему уравнений:
у = кх;
у = х2 + 4.
2. Приравняйте правые части
кх = х2 + 4.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

33.

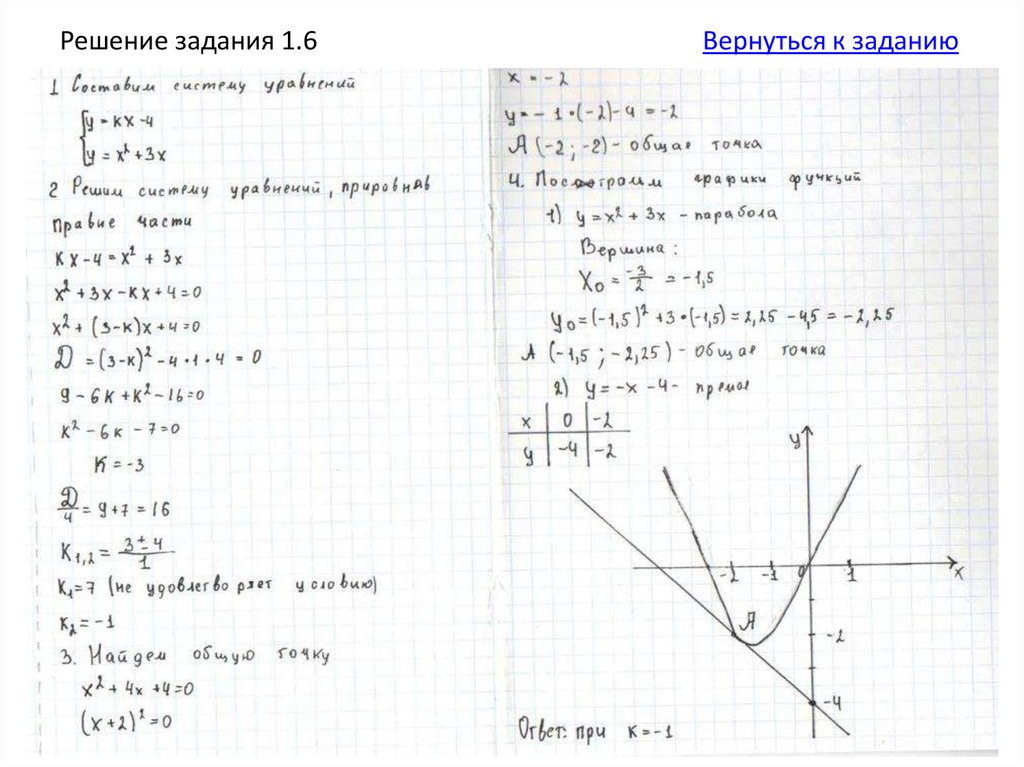
1.Составьте систему уравнений:
у = кх – 4;
у = х2 + 3х.
2. Приравняйте правые части
кх – 4 = х2 + 3х.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

34.

1.Составьте систему уравнений:
у = х2+ р;
у = - 2х.
2. Приравняйте правые части
х2+ р = - 2х.
3. Найдите дискриминант
получившегося квадратного
уравнения и приравняйте его к нулю.
Вернуться к заданию.

35.

1.Составьте систему уравнений:
у = 2х + в;
х2 + у2 = 5.
2. Вместо у во 2 уравнение
подставьте выражение (2х + в)
х2 + (2х + в)2 = 5.
3. Найдите дискриминант
получившегося квадратного
уравнения.
Вернуться к заданию.

36.

1.Найдите подмодульные нули.
2. Разбейте прямую на промежутки.
3. Раскройте модули Іх - 3І и Іх + 3І.
4. Постройте график получившейся
кусочной функции.
Вернуться к заданию.

37.

1.Найдите подмодульные нули.
2. Разбейте прямую на промежутки.
3. Раскройте модули Іх + 1І и Іх – 1І.
4. Постройте график получившейся
кусочной функции.
Вернуться к заданию.

38.

1.Найдите подмодульные нули.
2. Разбейте прямую на промежутки.
3. Раскройте модуль ІхІ.
4. Постройте график получившейся
кусочной функции.
Вернуться к заданию.

39.

40.

41.

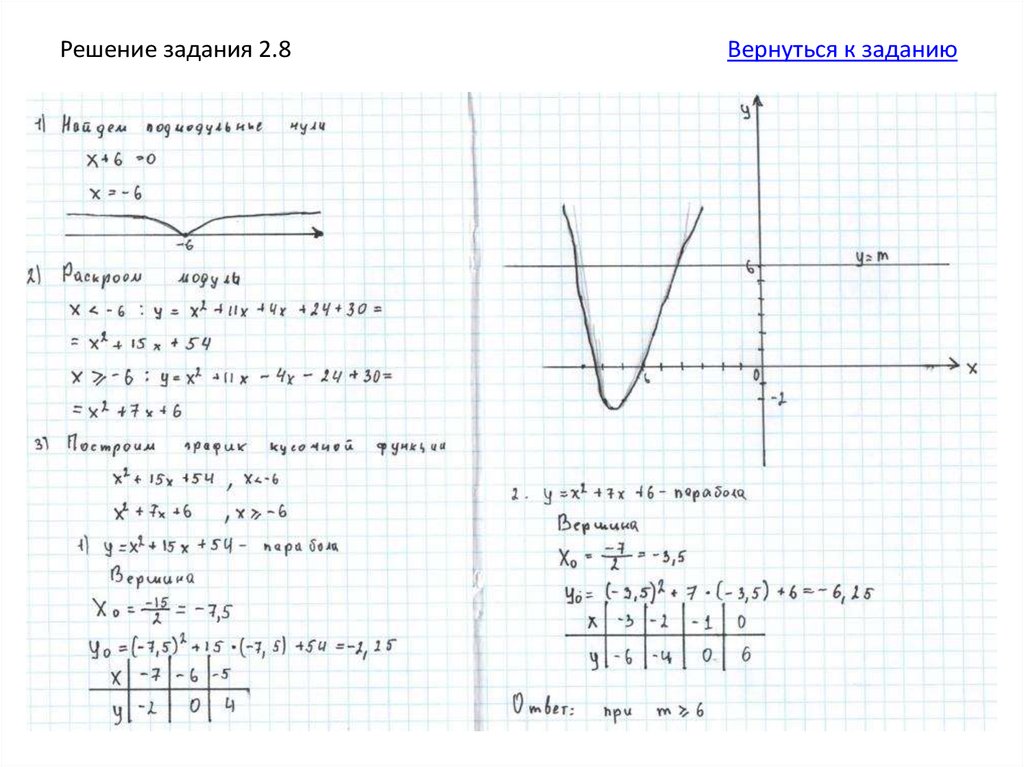
42.

1.Найдите подмодульные нули.
2. Разбейте прямую на промежутки.
3. Раскройте модуль Іх + 6І.
4. Постройте график получившейся
кусочной функции.
Вернуться к заданию.

43.

44.

1.Составьте систему уравнений, подставив
координаты точек А, В, С вместо х и у в
формулу у = ах2 + вх + с:
6 = а · 02+ в·0 + с;
-6 = а · 62+ в·6 + с;
9 = а · 12+ в·1 + с
2. Из первого уравнения найдите с, подставьте
его значение во 2 и 3 уравнения.
3. Решите получившуюся систему.
Вернуться к заданию.

45.

1.Составьте систему уравнений, подставив
координаты точек А, В, С вместо х и у в
формулу у = ах2 + вх + с:
4 = а · 02+ в·0 + с;
11 = а · 12+ в·1 + с;
- 1 = а · (- 5)2+ в·(- 5) + с
2. Из первого уравнения найдите с, подставьте
его значение во 2 и 3 уравнения.
3. Решите получившуюся систему.
Вернуться к заданию.

46.

1.Составьте систему уравнений, подставив
координаты точек А, В, С вместо х и у в
формулу у = ах2 + вх + с:
- 6 = а · 02+ в·0 + с;
-9 = а · 12+ в·1 + с;
6 = а · 62+ в·6 + с
2. Из первого уравнения найдите с, подставьте
его значение во 2 и 3 уравнения.
3. Решите получившуюся систему.
Вернуться к заданию.

47.

1.Составьте систему уравнений, подставив
координаты точек К, L, M вместо х и у в
формулу у = ах2 + вх + с:
- 2 = а · 02+ в·0 + с;
6 = а · 42+ в·4 + с;
3 = а · 12+ в·1 + с
2. Из первого уравнения найдите с, подставьте
его значение во 2 и 3 уравнения.
3. Решите получившуюся систему.
Вернуться к заданию.

48.

1.Составьте систему уравнений, подставив
координаты точек К, L, M вместо х и у в
формулу у = ах2 + вх + с:
- 5 = а · 02+ в·0 + с;
3 = а · 42+ в·4 + с;
10 = а · (-3)2+ в·(-3) + с
2. Из первого уравнения найдите с, подставьте
его значение во 2 и 3 уравнения.
3. Решите получившуюся систему.
Вернуться к заданию.

Общая теория. Графики. Тренажер

2. Общая теория

3. Теория к заданиям вида 1.

12. Теория к заданиям вида 2.

21. Теория к заданиям вида 3.

50. Решение задания 1.1 Вернуться к заданию

51. Решение задания 1.2 Вернуться к заданию

52. Решение задания 1.3 Вернуться к заданию

53. Решение задания 1.4 Вернуться к заданию

54. Решение задания 1.5 Вернуться к заданию

55. Решение задания 1.6 Вернуться к заданию

56. Решение задания 1.7 Вернуться к заданию

57. Решение задания 1.8 Вернуться к заданию

58. Решение задания 2.1 Вернуться к заданию

59. Решение задания 2.2 Вернуться к заданию

60. Решение задания 2.3 Вернуться к заданию

61. Решение задания 2.4 Вернуться к заданию

62. Решение задания 2.5 Вернуться к заданию

63. Решение задания 2.6 Вернуться к заданию

64. Решение задания 2.7 Вернуться к заданию

65. Решение задания 2.8 Вернуться к заданию

66. Решение задания 3.1 Вернуться к заданию

67. Решение задания 3.2 Вернуться к заданию

68. Решение задания 3.3 Вернуться к заданию

69. Решение задания 3.4 Вернуться к заданию

70. Решение задания 3.5 Вернуться к заданию