Похожие презентации:
Линейная и квадратичная функции и их графики
1. Линейная и квадратичная функции и их графики
2. Цель урока:
• повторить определение линейной иквадратичной функций, название и вид
графиков,
• зависимость расположения графиков
функций от коэффициентов,
• сформулировать план построения графиков
линейной и квадратичной функций, и план
определения функции по заданному
графику.
3. Функция вида y = kx + b, где k и b числа, x и y переменные, называется линейной функцией.
x – независимая переменная (аргумент)y – зависимая переменная (функция)
4. Графиком линейной функции y = kx + b является прямая линия
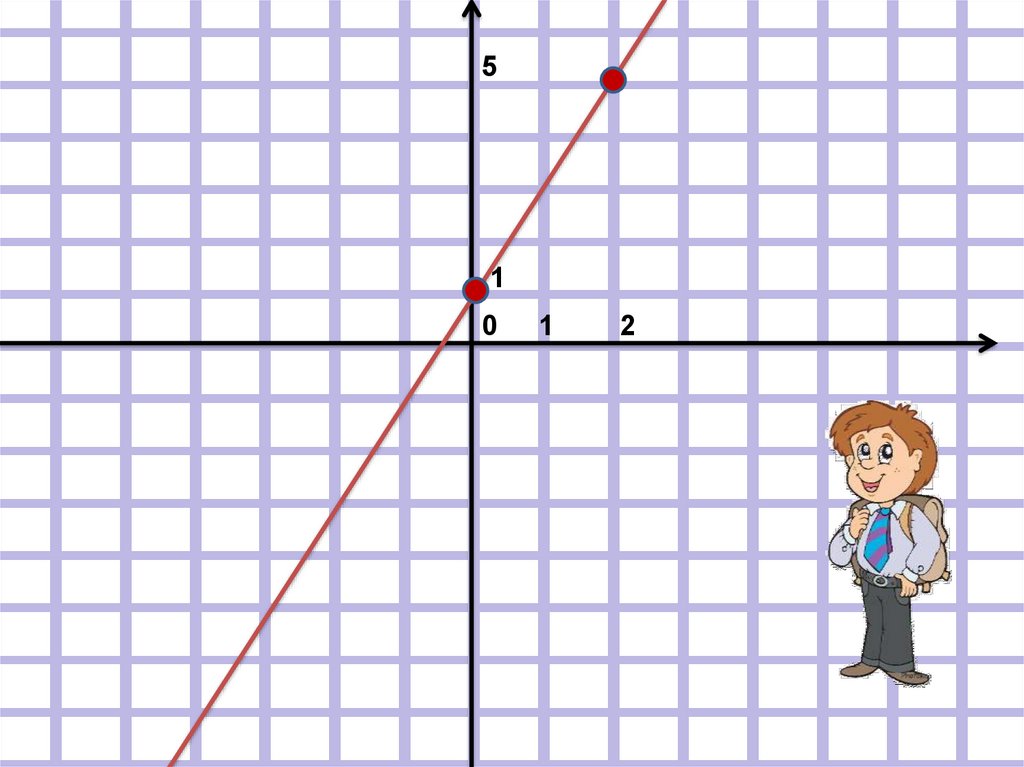
Построим график функции у = 2х + 1х
у
0
1
2
5
5.
51
0
1
2
6. k - угловой коэффициент
Если k > 0, то угол, образованныйграфиком функции и осью ОХ
острый
у = 3х - 1
х
у
0
-1
2
5
7.
50
-1
1
2
8.
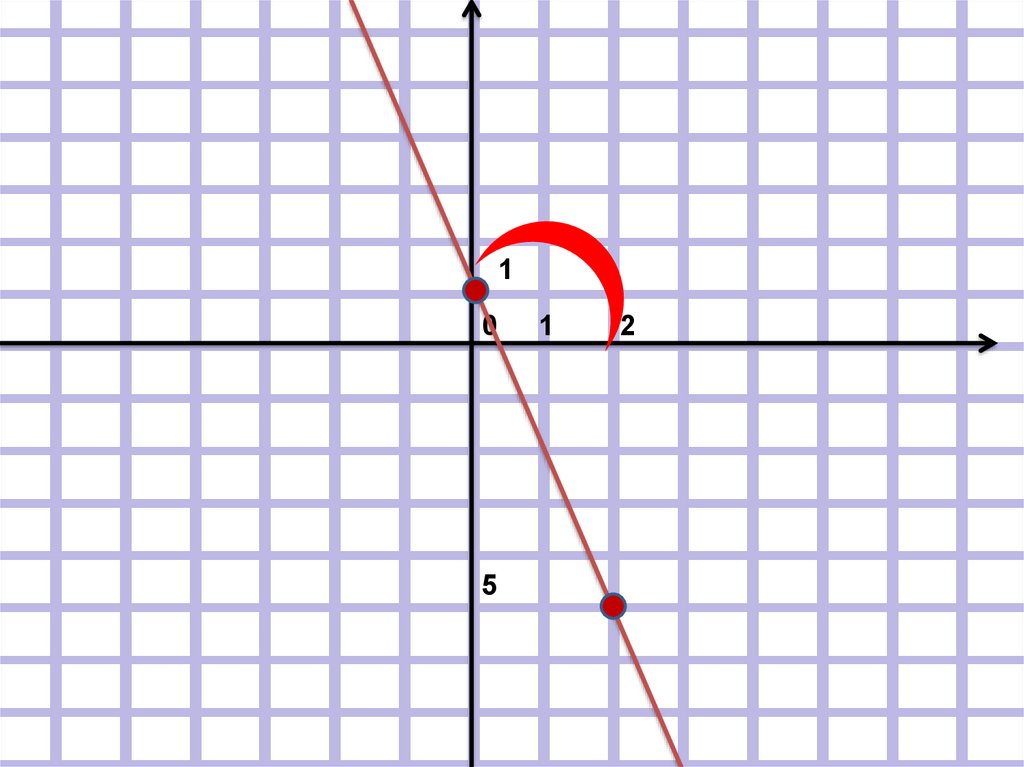
Если k ˂ 0, то угол, образованныйграфиком функции и осью ОХ
тупой
у = -3х + 1
х
у
0
1
2
-5
9.
10
5
1
2
10.
Если k = 0, то график функциипараллелен оси ОХ
у=3
х
у
0
3
2
3
11.
30
1
2
12.
Если у линейных функций угловыекоэффициенты одинаковы, то
график функций параллельны
у = 2х
х
у
0
0
2
4
У = 2х +1
х
у
0
1
2
5
13.
51
0
1
2
14. Коэффициент b (свободный коэффициент) показывает точку пересечения графика функции с осью ОУ
у = 3х - 1х
у
0
-1
2
5
15.
50
1
-1
2
16. Функция вида y = аx² + bх + с, где а ≠ 0, называется квадратичной функцией. Графиком функции является парабола.
17.
Направление ветвей параболыопределяются значениями
коэффициента а,
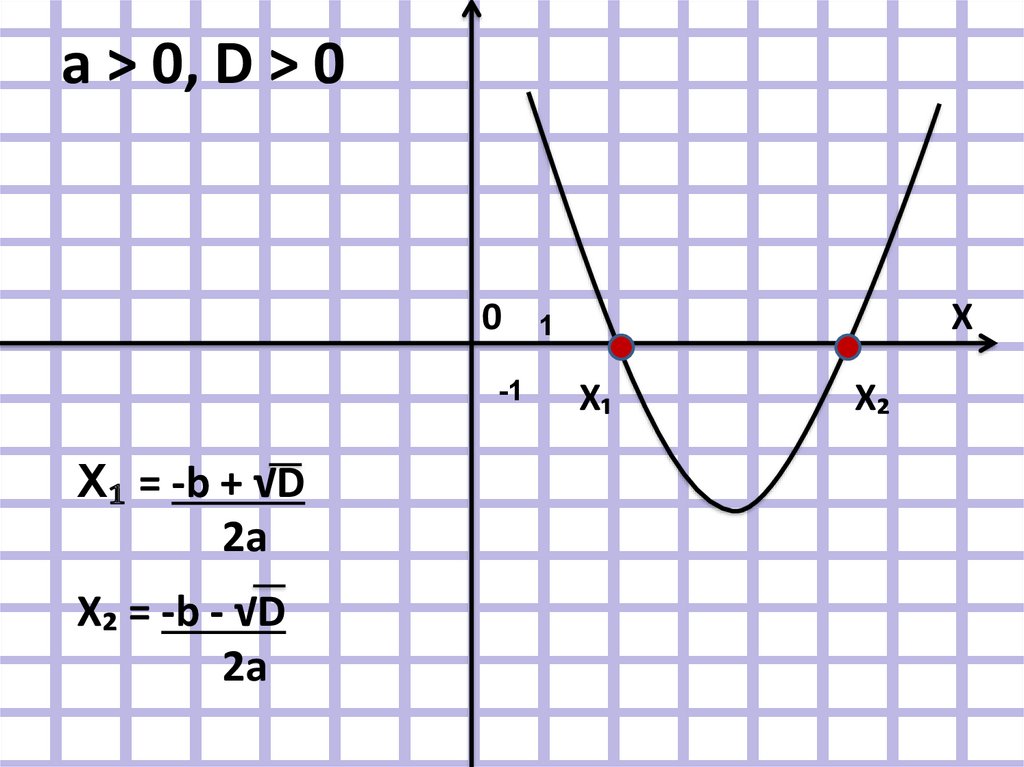
а ˃ 0, ветви направлены вверх
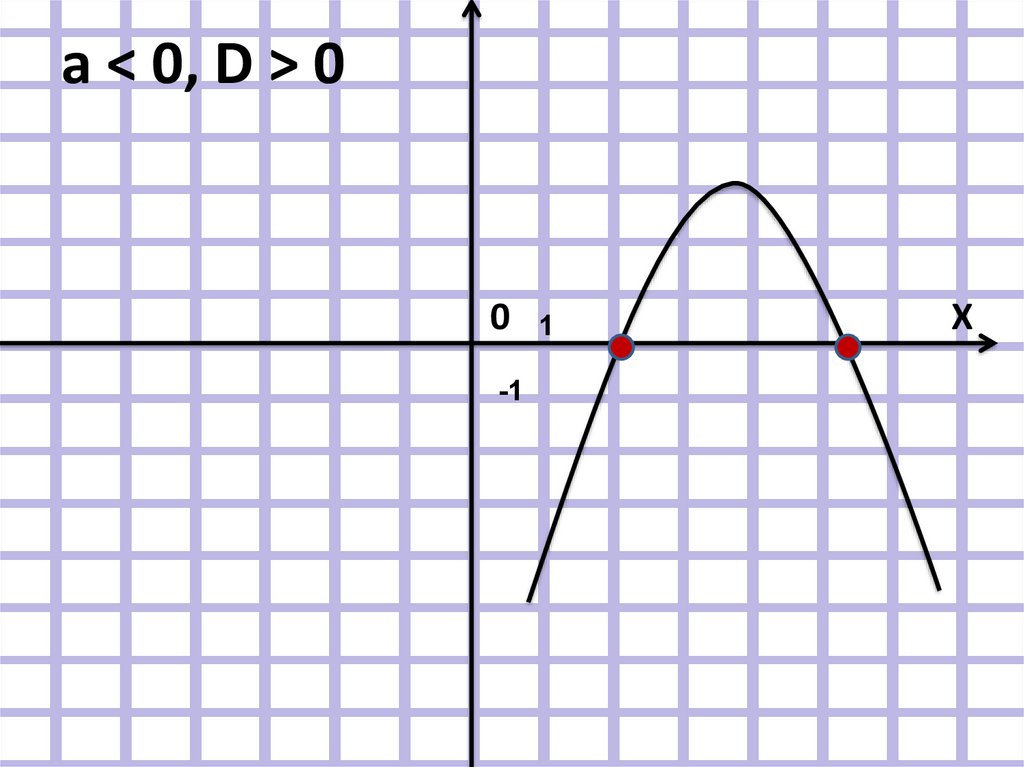
а ˂ 0, ветви направлены вниз.
18.
Пересечение параболы с осью ОХопределяется дискриминантом
D = b2 - 4ac,
D ˃ 0, две точки пересечения
D = 0, одна точка пересечения
D ˂ 0, нет точек пересечения
19.
а ˃ 0, D ˃ 00
-1
Х₁ = -b + √D
2a
Х₂ = -b - √D
2a
Х
1
Х₁
Х₂
20.
а ˃ 0, D = 00
Х
1
-1
Х₁=Х₂
21.
а ˃ 0, D ˂ 00
-1
1
Х
22.
а ˂ 0, D ˃ 00
-1
1
Х
23.
а ˂ 0, D = 00
-1
1
Х
24.
а ˂ 0, D ˂ 00
-1
1
Х
25.
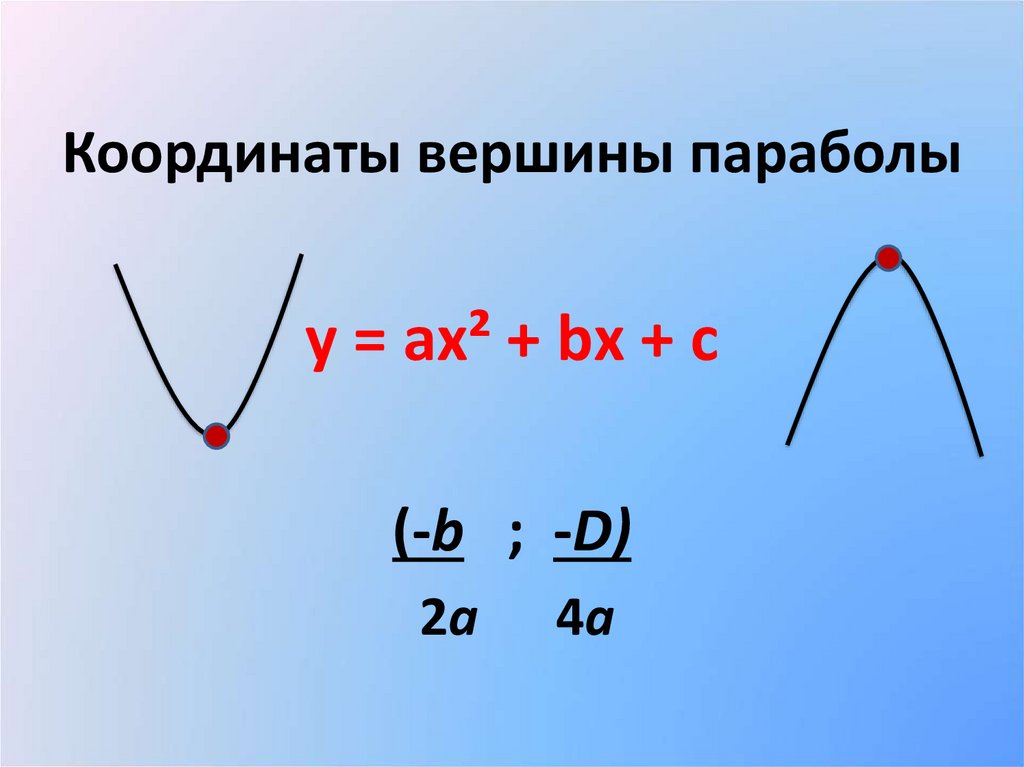
Координаты вершины параболыy = аx² + bх + с
(-b ; -D)
2a
4a
26.
У1
0
(-b ; -D)
2a
4a
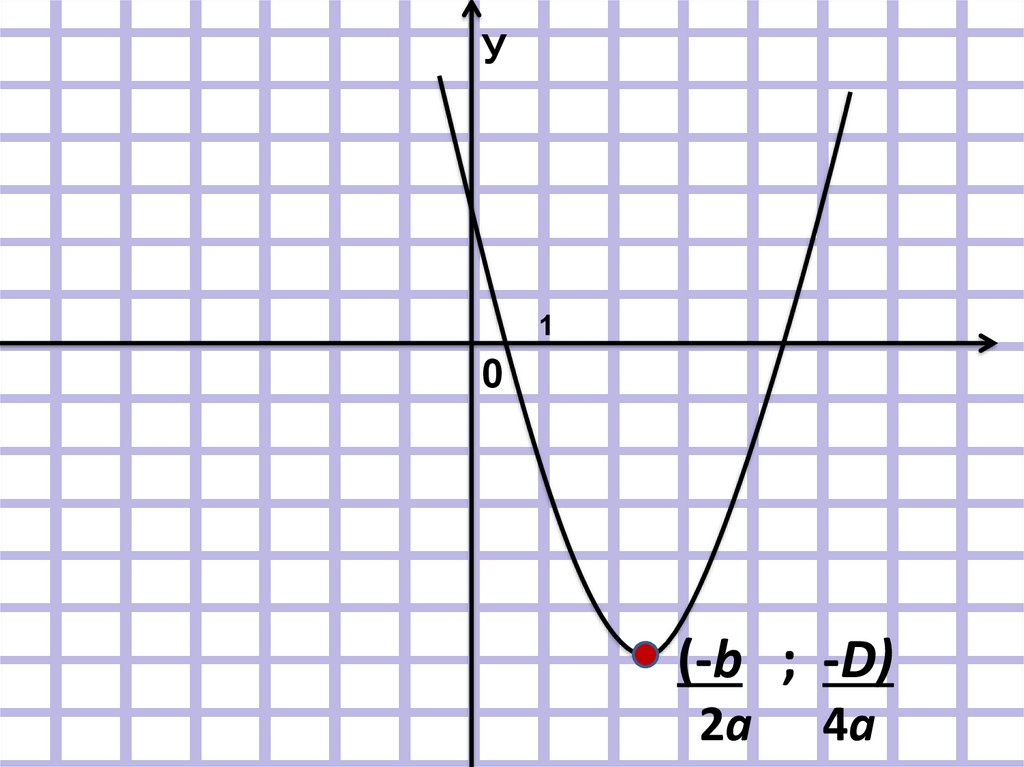
27.
Прямая х = -b является осью2a
симметрии параболы
28.
У1
0
(-b ; -D)
2a
4a
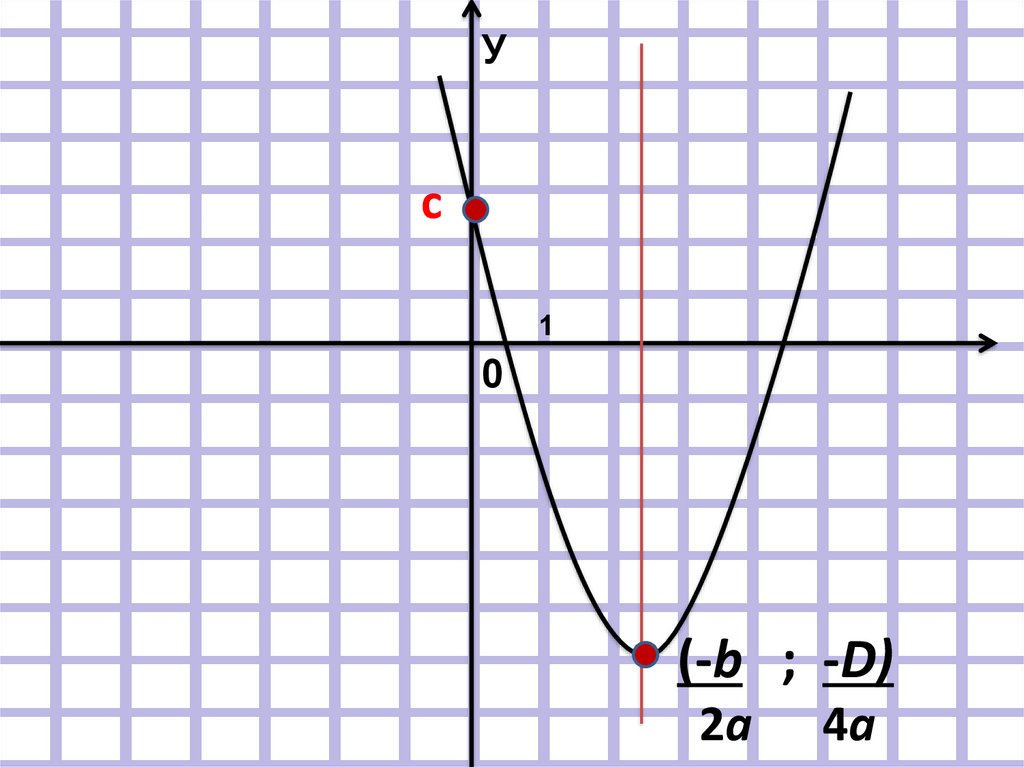
29. Для функции y = аx² + bх + с коэффициент с (свободный коэффициент) показывает точку пересечения графика с осью ОУ
30.
Ус
1
0
(-b ; -D)
2a
4a
31.
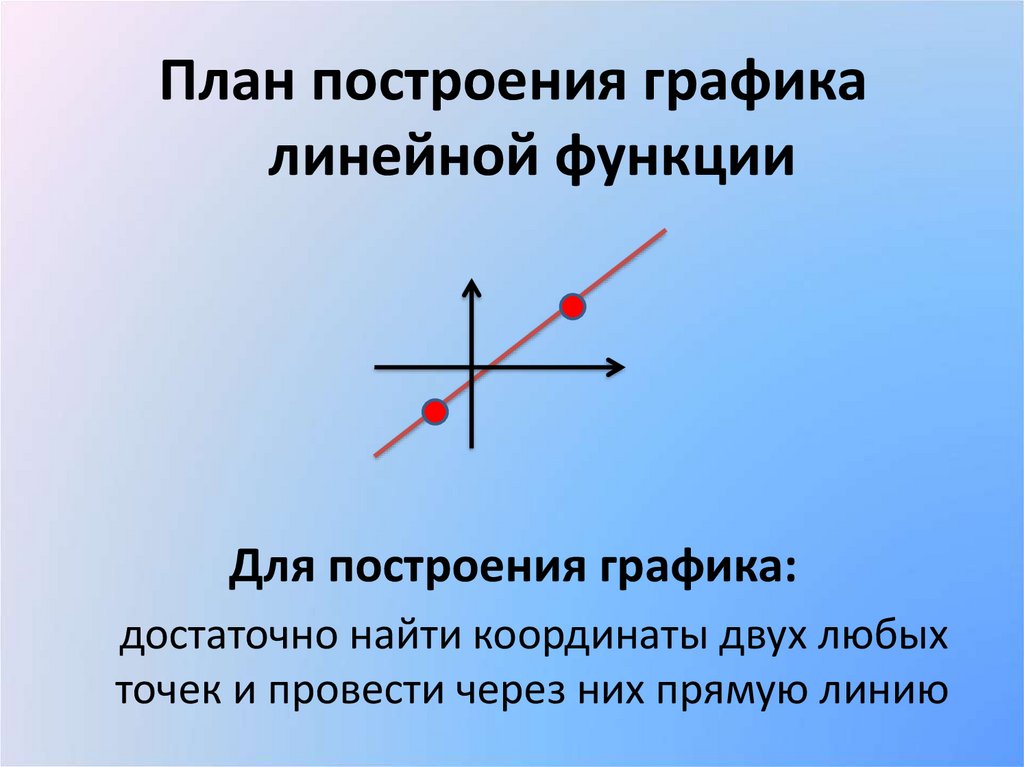
План построения графикалинейной функции
Для построения графика:
достаточно найти координаты двух любых
точек и провести через них прямую линию
32. План определения функции по заданному графику
Для определения функции по заданномуграфику необходимо:
• по значению коэффициента k определить угол,
образованный графиком функции и осью ОХ,
• по значению коэффициента b определить
пересечение графика функции с осью ОУ,
• если k=0, то график функции располагается
параллельно оси ОХ, и пересекает ось ОУ в
точке (0, b).
33. План построения графика квадратичной функции
• по значению коэффициента a определить направлениеветвей параболы,
• найти значение дискриминанта D и определить
количество точек пересечения параболы с осью ОХ,
• найти координаты вершины параболы (-b ; -D)
2a
4a
• по значению коэффициента с определить точку
пересечения параболы с осью ОУ, координаты точки
пересечения (0, с)
• построить точку симметричную точке (0, с),
• соединить плавной линией полученные точки.
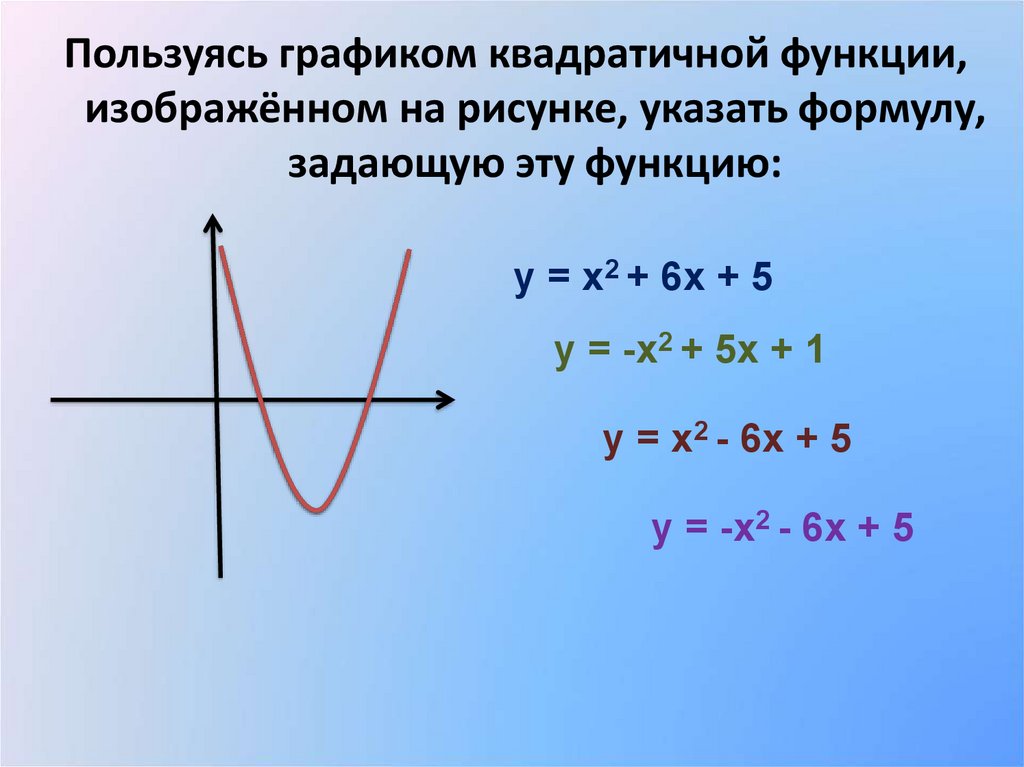
34.
Пользуясь графиком квадратичной функции,изображённом на рисунке, указать формулу,
задающую эту функцию:
у = х2 + 6х + 5
у = -х2 + 5х + 1
у = х2 - 6х + 5
у = -х2 - 6х + 5
35. Спасибо за просмотр
И удачноговыполнения
самостоятельной
работы


























 Математика
Математика








