Похожие презентации:
Неравенства. Литература
1. Неравенства.
Учитель Бузецкая Т.В.2. Литература.
1).Кузнецова Л.В.«Сборник заданий для проведения письменного экзамена по
алгебре» «Дрофа», 2007 год
2). Кузнецова Л.В.
«Сборник заданий для подготовки к итоговой аттестации в
9 классе» «Просвещение», 2010 год
3).Лысенко Ф.Ф. «Алгебра 9 класс тематические тесты для
подготовки к ГИА 2010» «Легион –М» 2009 год
4). Лысенко Ф.Ф. «Подготовка к итоговой аттестации 2010»
2009 год
3.
1). Определение2). Виды
3). Свойства числовых неравенств
4). Основные свойства неравенств
4). Типы
5). Способы решения
4.
Запись видаа>в или а<в
называется
неравенством.
5.
Неравенства вида а≥в,а≤в называется ……
Неравенства вида а>в,
а<в называется……
6.
1). Если а>в, то в<а.2).Если а>в, в>с, то а>с.
3). Если а>в, с-любое число, то
а+с>в+с.
4). Если а>в, с>х, то а+с>в+х.
5). Если а>в, с>0, то ас>вс.
6). Если а>в, с<0, то ас<вс.
7). Если а>о, с>0,то à n > c n .
8). Если а>о, с>0, а>с, то n à > n ñ;
àn
7.
1). Любой членнеравенства можно
переносить из одной
части неравенства в
другую, изменив его знак
на противоположный,
при этом знак
неравенства не меняется.
8.
2).Обе части неравенстваможно умножить или
разделить на одно и тоже
положительное число, при
этом знак неравенства не
изменится. Если это число
отрицательное, то знак
неравенства изменится на
противоположное.
9.
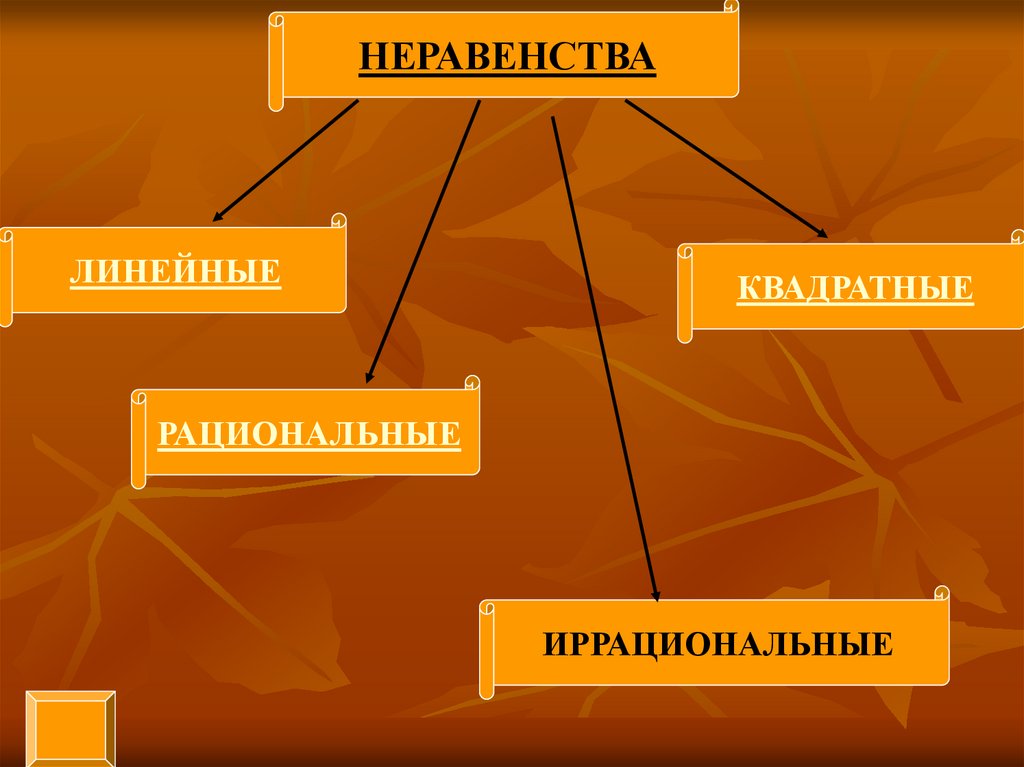
НЕРАВЕНСТВАЛИНЕЙНЫЕ
КВАДРАТНЫЕ
РАЦИОНАЛЬНЫЕ
ИРРАЦИОНАЛЬНЫЕ
10.
I).Линейное неравенство.1). х+4<0;
2).2х+4≥6;
х<-4;
2х≥-2;
-4
х
х≥-1;
Ответ: (-∞;-4).
-1
х
Ответ: [-1;+∞).
11. 1.Решить неравенства.
1). х+2≥2,5х-1;2).х- 0,25(х+4)+0,5(3х-1)>3;
3).
4).х²+х<х(х-5)+2;
5). 9 x 2 10 x 2 2.
10
9
12. 2. Найдите наименьшие целые числа, являющиеся решениями неравенств
1.2(х-3)-1-3(х-2)-4(х+1)>0;2.0,2(2х+2)-0,5(х-1)<2.
3.
Найдите наименьшие натуральные
числа, являющиеся решениями
неравенства
3х-3<1,5х+4.
13.
II).Квадратные неравенства.Способы решения:
Графический
С применением
систем
неравенств
Метод
интервалов
14.
1.1).Метод интервалов(для решения квадратного уравнения)
ах²+вх+с>0
1). Разложим данный многочлен на множители,
т.е. представим в виде
а(х- õ1)(х- õ2)>0.
2).корни многочлена нанести на числовую ось;
3). Определить знаки функции в каждом из
промежутков;
4). Выбрать подходящие интервалы и записать
ответ.
õ1
15.
õ õ 6 02
x²+x-6=0; (х-2)(х+3)=0;
x1 3; x2 2.
Ответ: (-∞;-3)v(2;+∞).
16. 1.Решение неравенства методом интервалов.
1). х(х+7)≥0;2).(х-1)(х+2)≤0;
3).х-х²+2<0;
4).-х²-5х+6>0;
5).х(х+2)<15.
17.
Домашняя работа:Сборник 1).стр. 109 № 128-131
Сборник 2).стр.111 №3.8-3.10; 3.22;3.37-3.4
18. 1.2).Решение квадратных неравенств графически
1). Определить направление ветвейпараболы, по знаку первого
коэффициента квадратичной функции.
2).Найти корни соответствующего
квадратного уравнения;
3).Построить эскиз графика и по нему
определить промежутки, на которых
квадратичная функция принимает
положительные или отрицательные
19. Пример:
х²+5х-6≤0y= х²+5х-6 (квадратичная функция, график
парабола, а=1, ветви направлены вверх)
х²+5х-6=0; корни этого уравнения: 1 и -6.
у
+
+
-6
1
x
Ответ: [-6;1].
20. Решите графически неравенства:
•Решите графически неравенства:1).х²-3х<0;
2).х²-4х>0;
3).х²+2х≥0;
4). -2х²+х+1≤0;
(0;3)
(-∞;0)U(4;+∞)
(-∞;-2]U[0;+∞)
(-∞;-0,5]U[1;+∞)
21.
Домашнее задание:Сборник 1).стр. 115 №176-179.
работы №47,45,42,17,12
(задание №5)
Сборник 2).стр. 116 № 4.4,4.5, 4.11.
работы №6, задание 13.
22. III).Рациональные неравенства вида решают методом интервалов.
P( x)Q( x)
1) Раскладывают на линейные множители
числитель P(x) и знаменатель Q(x). Если это
удается, то дальше поступают так.
2) На числовую ось наносят корни всех
линейных множителей. На каждом из
промежутков, на которые эти точки
разбивают ось, дробь P(x)/ Q(x). сохраняет
знак
3) Определяют знак дроби на каждом
промежутке.
4) Записывают ответ.
23.
Сборник 1).стр. 109 №132Сборник 2). Стр. 112-113 № 3.20, 3.21,
3.39-3.42
24.
Системы неравенств.25.
1). Содержащие линейные неравенства.2). Содержащие квадратное(рациональное)
неравенство и линейное неравенство.
3). Содержащие квадратные неравенства.
4). Двойное неравенство, которое решается с
помощью систем.
5). Неравенства с модулем
26.
1). 5х+1>62x-4<3 ;
5x>5
2x<7 ;
x>1
x<3,5.
1
3,5 x
Ответ: (1;3,5).
Задания:
Сборник 1). Стр. 111№139-142
стр. 170-172 № 711-766
Сборник 2).стр. 110 № 3.4-3.7
27.
2). х²-1>0x+4<0;
(x-1)(x+1)>0
x<-4;
+
+
-4 -1
1
x
Ответ: (-∞;-4).
Задания:
Сборник 1).стр. 111 № 143-145
Сборник 2). Стр. 112-113 №3.24, 3.25
28.
3). х²-4>0x²-3x+5<0.
Решаем каждое квадратное неравенство в
отдельности. Изображаем решения на
числовой прямой и смотрим пересечения
этих решений. Записываем ответ.
Задания:
Сборник 1). Стр. 111 № 146-147
Сборник 2).стр. 113, 115 № 3.27, 3.29,
3.47, 3.48
29.
4). -12<x-1<1x-1<1
x<2
Ответ: (-11;2).
x-1>-12;
x>-11.
Задания:
Сборник 1).стр. 109 № 126-127, 134,
стр. 172 №783-790
Сборник 2). Стр. 111 №3.9
30.
5).| 3х-2|<102
3x-2>-10
x> 2
3
3x-2<10;
x<4.
Ответ: ( 2 2 ;4).
3













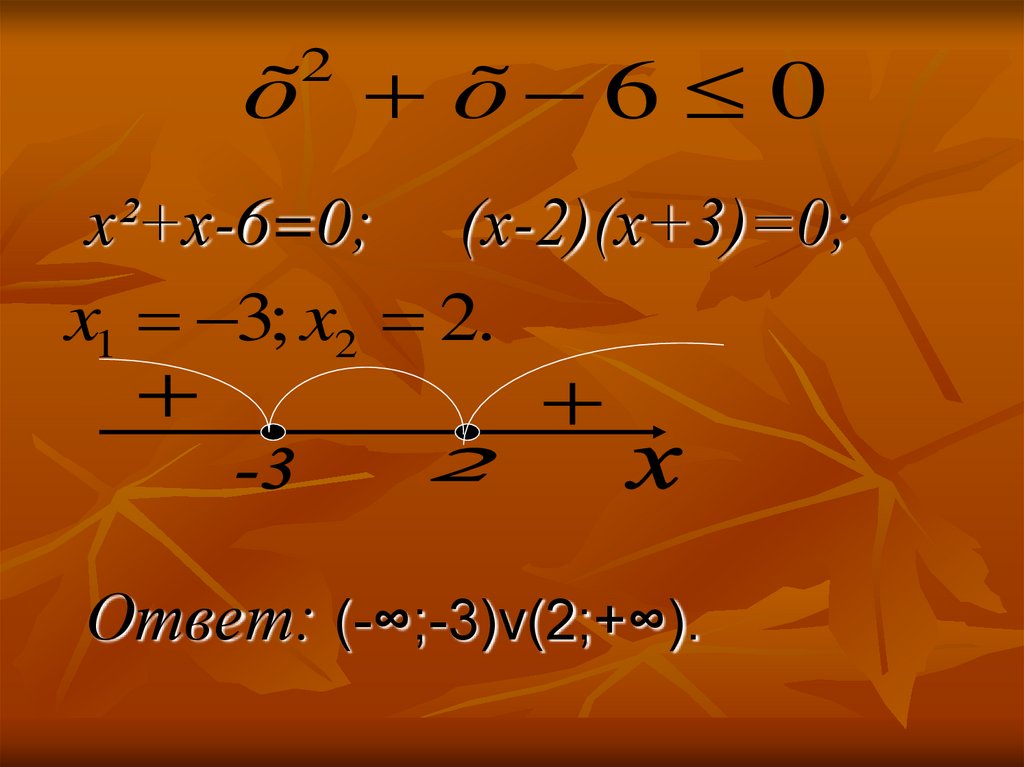















 Математика
Математика








