Равносильные уравнения, уравнения следствия, уравнения, содержащие знак модуля

1.

МАТЕМАТИКА
Уравнения:
равносильные уравнения,
уравнения следствия
уравнения, содержащие знак
модуля
Лекцию подготовили: Спицына Татьяна, Суворова Ольга
Руководитель: Калугина Екатерина Евгеньевна

2.

ЛЕКЦИЯ№3
Литература
В помощь учащимся лицея –
интерната при СГАУ им. Н. И. Вавилова «
Сборник задач по математике Часть I»
Уравнения:
равносильные уравнения,
уравнения следствия,
уравнения, содержащие знак модуля.

3.

План лекции
Равносильные уравнения
Уравнения следствия
Определение модуля действительного числа
Алгоритмы решения уравнений, содержащих
знак модуля:
f(x) a, a R

4.

Определение
Выражение, состоящее из чисел, переменных ,
знаков арифметических и алгебраических
операций, скобок, знака равенства, называется
уравнением.
2x 3 5
x 2 4x 3 0
2
3
5
2
1 x 1 x
1 x
x 4 3
log 2 (3x 4) 2
22x 2x 6 0
sin2x cosx 0

5.

Определение
Корнем уравнения называется такое значение переменной,
при подстановке которого в уравнение оно обращается в
истинное равенство.
Решить уравнение это значит найти все его корни или
доказать что таковых нет.
Пример1 2x 3 5
Решение
2x 3 5,
2x 8,
x 4.
Ответ: - 4.
2
Пример2
x
3x 4 0
Проверка
Решение
x 2 3x x
4 0, 4
x 2 3x 4 2(
0, 4) 3 5,
D b 2 4ac;
8 3 5,
2
D 3 4 4 9 16 7;
5 5.
D 0
Ответ: уравнение корней не
имеет.

6.

Определение
Уравнения называются равносильными, если
множества их решений совпадают или они не
имеют решений.
Пример
1 уравнение
x 2 2x 15 0.
2 уравнение
2
2x
5.
2x
3 1 0.
x 1.
Корни 2 уравнения: нет
x 1.
Корни 1 уравнения: нет.
Уравнения равносильны, так как
онимножества
решений неих
имеют.
решений совпадают.

7.

Определение
Пусть даны 2 уравнения
f(x) g(x)
и
p(x) q(x)
.
Если любой корень 1 уравнения является корнем 2
уравнения, то 2 уравнение называют уравнением
следствием 1.
Пример
1 уравнение
x 2 1.
2 уравнение
x 1.
Корни 1 уравнения: x 1. Корни 2 уравнения:
2 уравнение является уравнением следствием 1
уравнения.
x 1.

8.

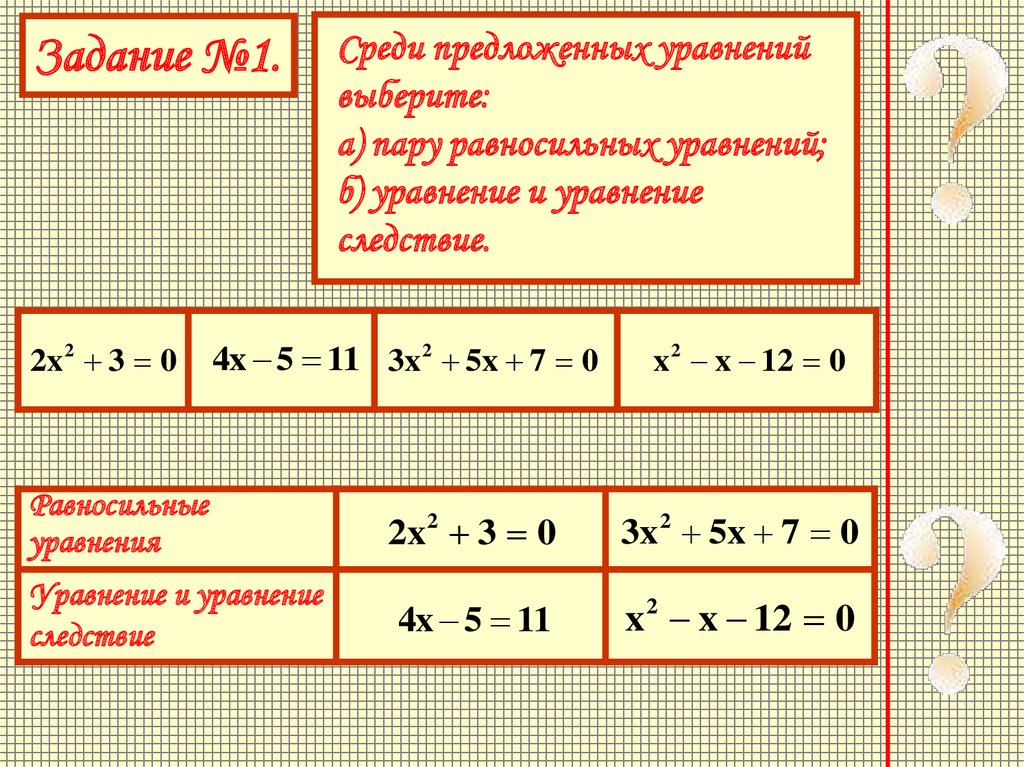
Задание №1.
2x 2 3 0
Среди предложенных уравнений
выберите:
а) пару равносильных уравнений;
б) уравнение и уравнение
следствие.
4x 5 11 3x 2 5x 7 0
x 2 x 12 0
Равносильные
уравнения
2x 2 3 0
3x 2 5x 7 0
Уравнение и уравнение
следствие
4x 5 11
x 2 x 12 0

9.

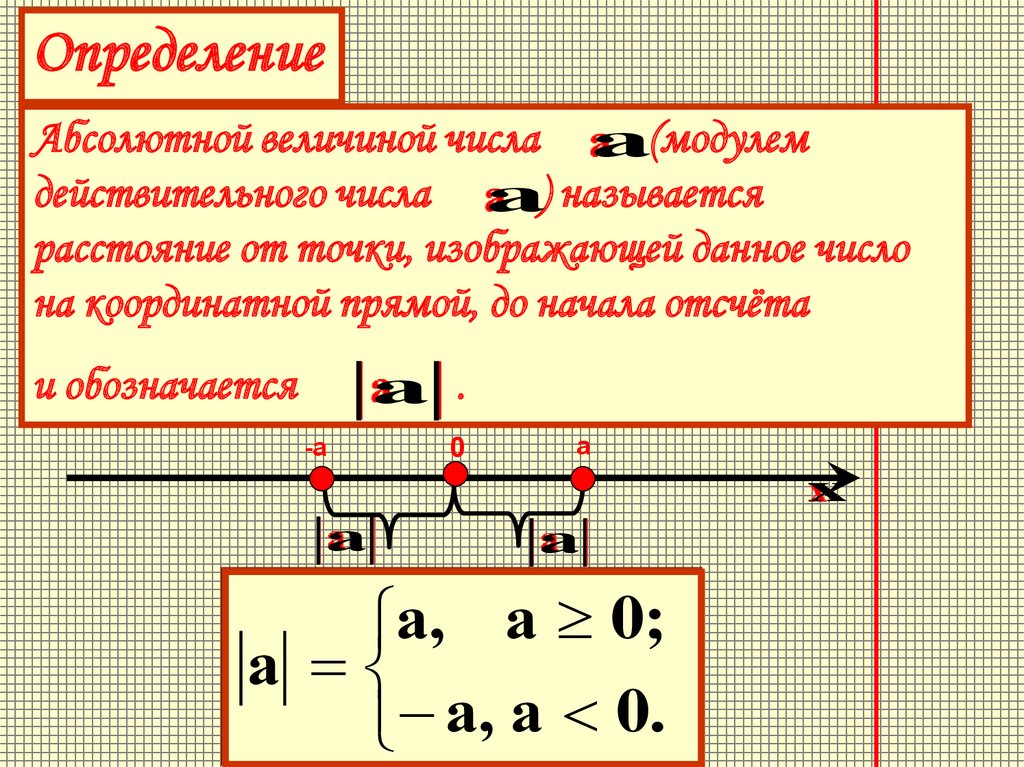
Определение
Абсолютной величиной числа а(модулем
действительного числа а) называется
расстояние от точки, изображающей данное числоа
на координатной прямой, до начала отсчёта
а .
и обозначается
-а
0
а
x
а
а
а, а 0;
а
а, а 0.

10.

Основные свойства модуля.
1
а 0
6
a b a b
2
а а
7
a b a b , ab 0
3
а а
8
a b a b, a 0 иb 0
9
a b a + b , ab 0
4
5
ab a b
a
a
, b 0 10
b
b
a b 0, a2 b2 0

11.

Определение
Уравнения, содержащие знак модуля, называются
уравнениями, содержащими знак модуля.
2х - 5 = 4
х2 - 2 х - 3 = 0
1- 2х = 6х +1
х 2 - 5х + 4 = 10
1 - 2х
х 5 - 2х +1 = 2х - 7 3х + 4
+ 2х - 5 = 3

12.

Алгоритм решения уравнения
f(x) a, a R
Если a 0
f(x) a
Если a 0
f(x) 0
Уравнение корней не
имеет
f(x) 0
I способ
Если a 0
II способ
f(x) a f(x) 0; f(x) a,
f(x) = a; f(x) a.
f(x) < 0;
f(x) = -a.

13.

2x 3 0
Пример 1
Решение
у
2 x 3 0,
2 x 3,
1
x 1,5,
x 1,5.
Ответ:
y = 2 x -3
1,5.
-1,5
0
1
1,5
х

14.

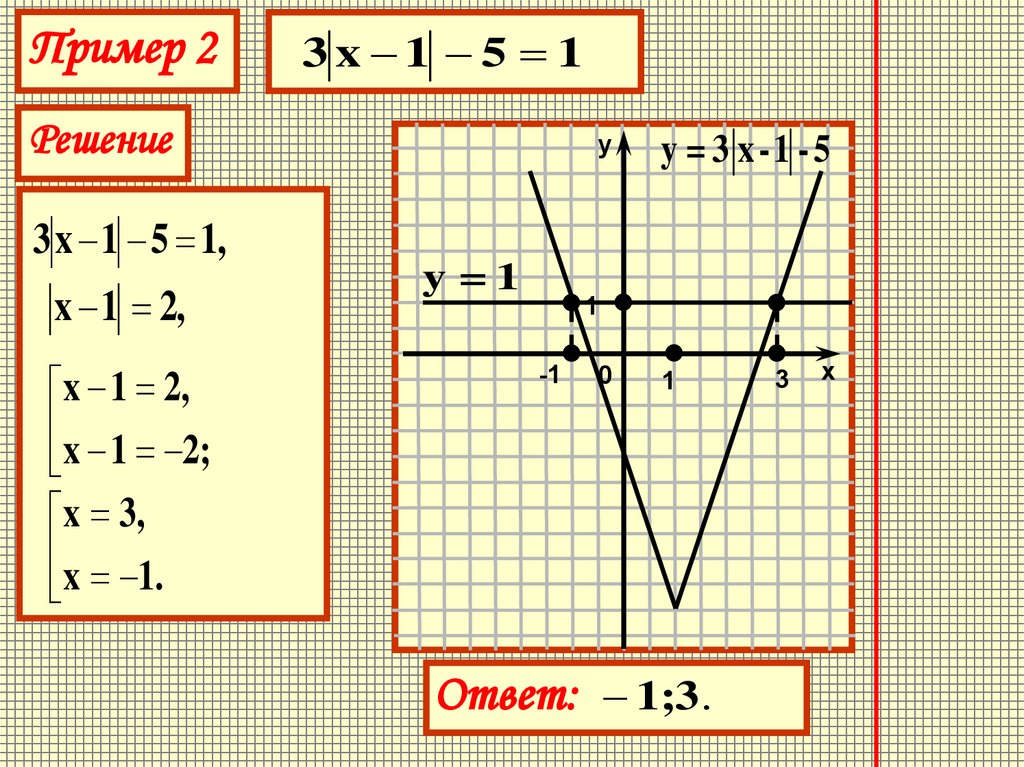
Пример 2
3 x 1 5 1
Решение
у
y = 3 x -1 - 5
3 x 1 5 1,
x 1 2,
x 1 2,
x 1 2;
x 3,
x 1.
y =1
1
-1
0
1
Ответ: 1;3.
3
х

15.

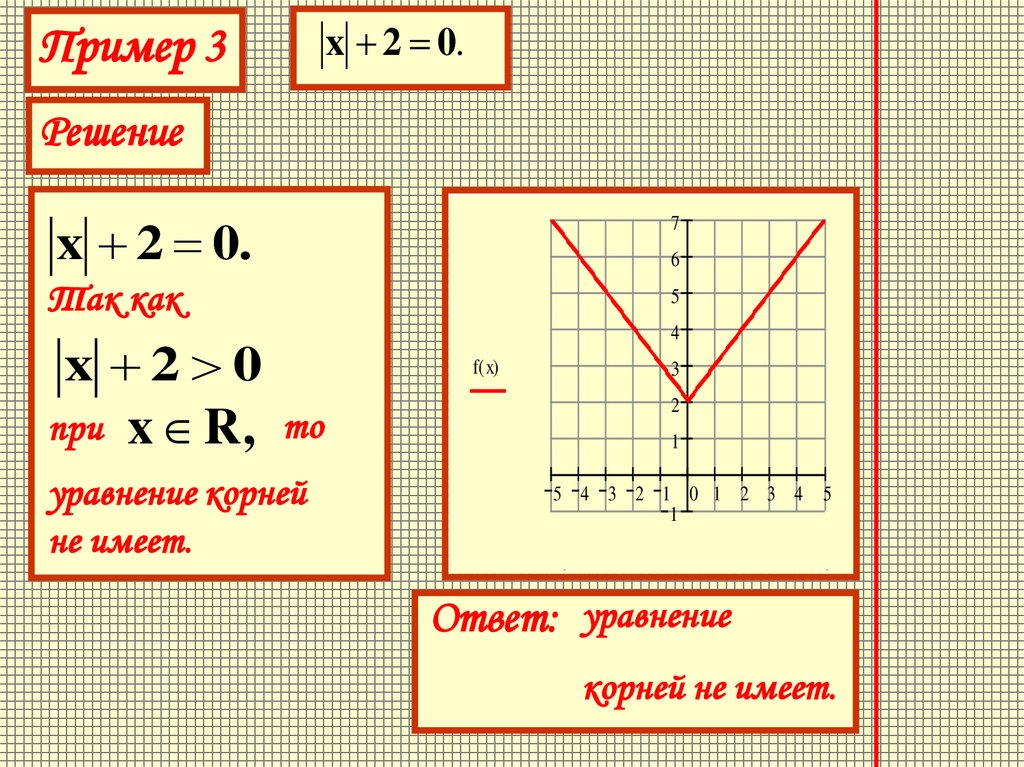
Пример 3
x 2 0.
Решение
x 2 0.
7
7
6
Так как
5
x 2 0
при x R, то
4
уравнение корней
не имеет.
f( x)
3
2
1
1
5 4 3 2 1 0 1 2 3 4 5
1
5
x
5
Ответ: уравнение
корней не имеет.

16.

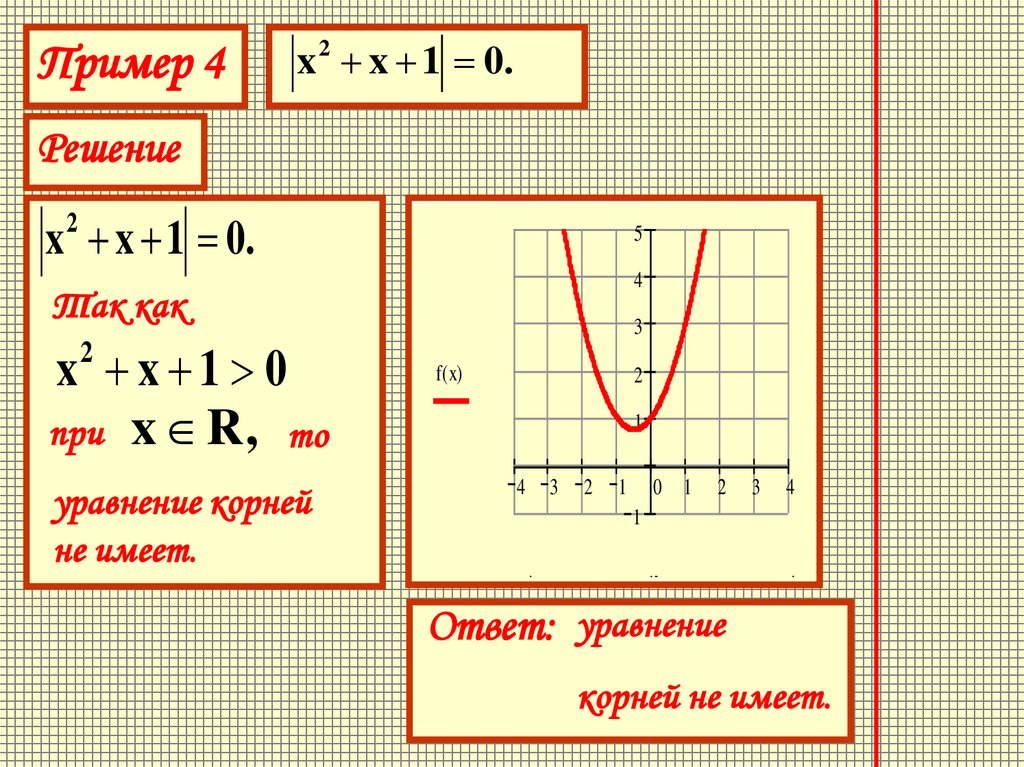
Пример 4
x 2 x 1 0.
Решение
x x 1 0.
2
5
5
4
Так как
x x 1 0
при x R, то
2
уравнение корней
не имеет.
3
f( x)
2
1
1
4
3
2
1
0 1
2
3
4
1
4
x
4
Ответ: уравнение
корней не имеет.

17.

Пример 5
x 2 2
Решение
у
x 2 2,
y = x -2
x 2 2,
x 2 2;
x 4,
x 0;
y=2
1
-4
0
1
x 4,
x 4,
x 0.
Ответ: 4;0.
4
х

18.

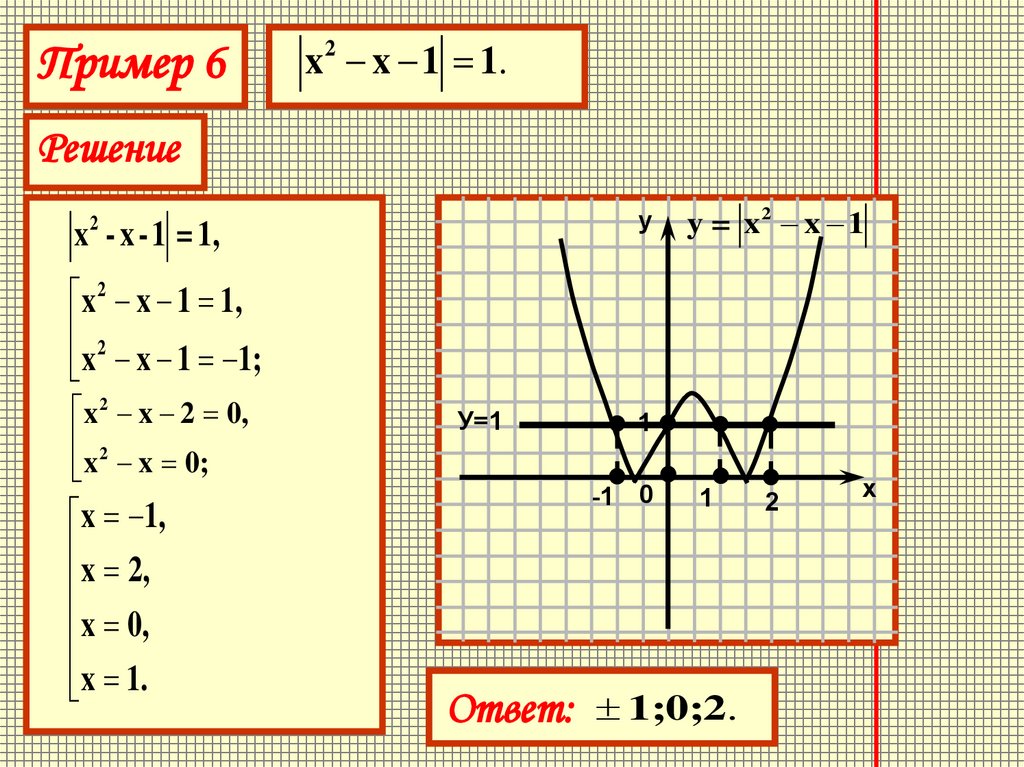
Пример 6
x 2 x 1 1.
Решение
у
2
x - x -1 = 1,
y = x2 x 1
x 2 x 1 1,
2
x x 1 1;
x 2 x 2 0,
2
x x 0;
x 1,
x 2,
x 0,
x 1.
У=1
1
-1 0
Ответ:
1
1;0;2.
2
х

19.

x2 2 x 3 0.(ЦТ 2003 г)
Пример 7
Решение
2
x - 2 x - 3 = 0. Так как x = x .
2
2
Тогда x 2 x 3 0 . Пусть x t, t 0 .
2
t 2 2t 3 0
t 0,
t 1,
t 3;
t
t
t
t
Вернёмся к
переменной х
0,
1,
0,
3;
t 3.
x 3,
x 3.
Ответ: 3.

20.

Пример 8
x x - 7x +12 = 0.
Решение
x x - 7x +12 = 0,
x 0,
2
x 7x 12 0,
x 0,
x 2 7x 12 0;
x 0,
2
x 7x 12 0,
x 0,
x 2 7x 12 0;
x 0,
x 3; x 4;
x 0,
7 97
;
x
2
x 3,
x 4,
x 7 97 .
2
Ответ:
7 97
;3;4.
2

21.

Пример 9
x 5x
2
Решение
2
x - 5x
x-2
x-2
x 2
x 2
14 0 (ЦТ 2004 г)
- 14 = 0,
x > 2,
x 2 0,
2
x 5x 14 0; x = -2;x = 7;
x 2 0,
x < 2,
2
x 5x 14 0; x = -7;x = 2;
x 7,
x 7.
Ответ: 7.

22.

Домашнее задание:
1) Материал лекции.
2) М.Л.Галицкий «Сборник задач по алгебре для 89 классов» §1п.6.
В помощь учащимся лицея-интерната при
СГАУ им. Н.И.Вавилова «Сборник задач по
математике. Часть I.» §5 стр. 74 ; 84.
3) М.Л.Галицкий «Сборник задач по алгебре для 89 классов» §5 №5.7;5.8.
В помощь учащимся лицея-интерната при
СГАУ им. Н.И.Вавилова «Сборник задач по
математике. Часть I.» §5 стр. 88 № 1 – 5 ; 9.