Похожие презентации:
Возведение степени в степень. Свойства действий со степенями
1.
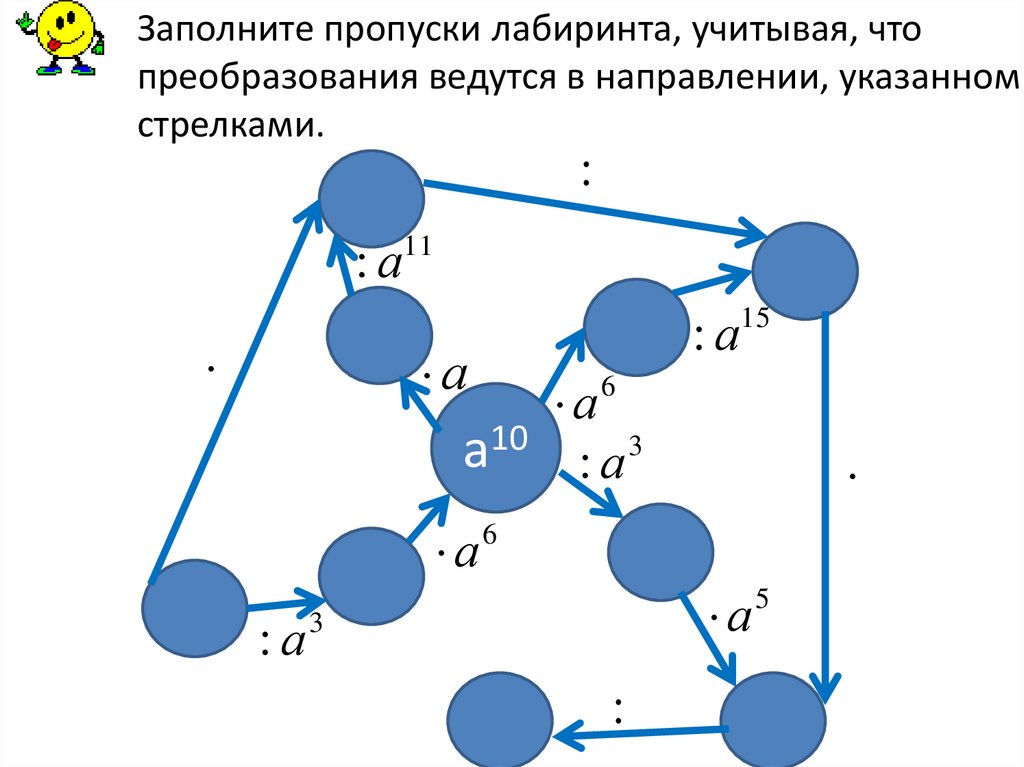
Заполните пропуски лабиринта, учитывая, чтопреобразования ведутся в направлении, указанном
стрелками.
:
:а
11
:а
а
:а
а
3
:а
6
а10
а
15
6
а
3
:
5
2.
3 свойствоСловесная формулировка: При возведении
степени в степень, основание остается прежним,
а показатели умножаются.
Математическая запись:
(a ) (a)
n m
nm
3.
(2 ) (2 2 2) 2 2 23 2
3 раза
3 раза
2 2 2 2 2 2 2
6 раз
3 2
2
6
4.
4 свойствоСловесная формулировка: При возведении
произведения в степень, нужно возвести в эту
степень каждый множитель, а полученные
степени умножить.
Математическая запись: (a b) m a m b m
5.
(2 5) (2 5) 2 5 (2 5)3
3 раза
2 2 2 5 5 5 2 5
3
3 раза
3 раза
3
6.
5 свойствоСловесная формулировка: При возведении
частного (дроби) в степень, нужно возвести в эту
степень числитель и знаменатель и разделить
полученные степени. m
a m a
Математическая запись:
( )
b
b
m
7.
3 раза2 3 2 2 2 2 2 2 2
( ) ( ) ( )
3
5
5 5 5
5 5 5 5
3
3 раза
3 раза
8.
Свойства действий со степенямиаn. аm =an+m, n, m – натуральное,
а – любое,
аn: аm =an-m, n,m – натуральное,
при а 0,
(аn ) m =anm, n,m – натуральное,
а – любое,
(ab)m=ambm m – натуральное,
а,b – любое,
(a/b)m=am/bm m – натуральное,
а – любое, b 0

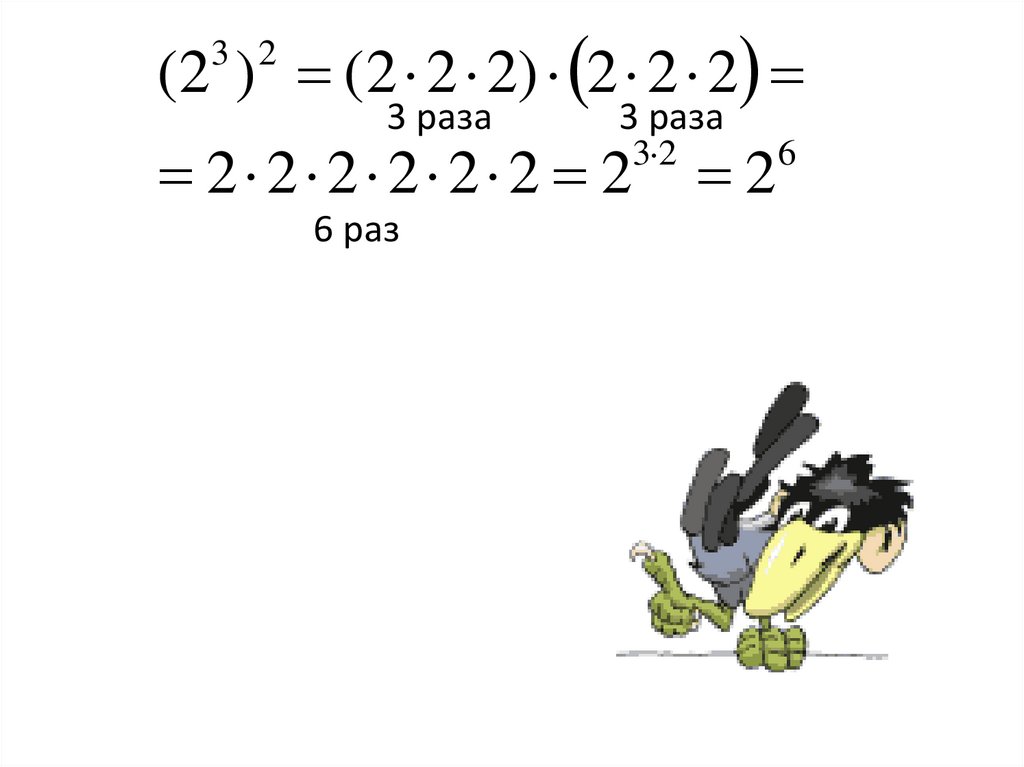

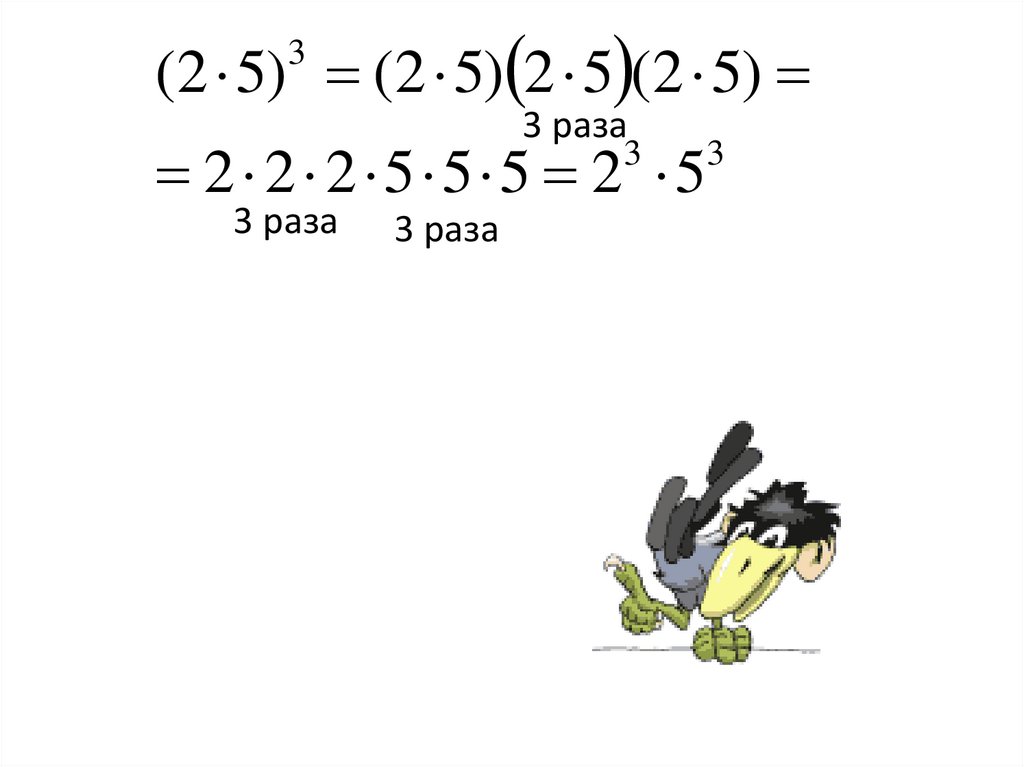

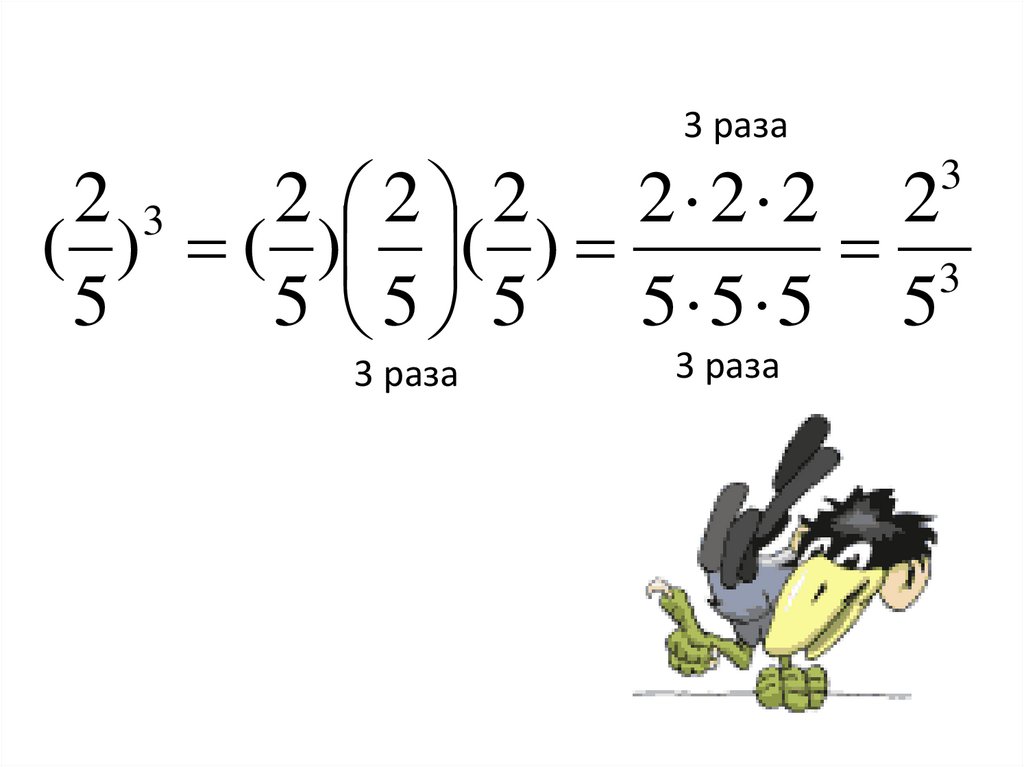

 Математика
Математика








