Похожие презентации:
Степени и корни. Свойства степеней
1. Степени и корни
2. СТЕПЕНЬ
3. Степенью называется выражение вида ас где: а – основание степени; с – показатель степени.
Степенью называется выражениевида
с
а
где:
а – основание степени;
с – показатель степени.
4. Степень с натуральным показателем {1, 2, 3,…} – это степень, показатель которой – натуральное число (т. е. целое и
положительное)5. а1 = а а2 = а *а а3 = а*а*а аn= а*а*а….*а n
6. Степень с целым показателем {0, ±1, ±2….}
Если показателем степени является целоеположительное число:
an= an
Возведение в нулевую степень:
а0=1
Если показатель степени является целое
отрицательное число:
7. Степень с рациональным показателем
а>0n- натуральное число
m- целое число
8. Свойства степеней
9.
Произведение степеней10. Деление степеней
11. Возведение степени в степень
12. КОРЕНЬ
13. Арифметический квадратный корень - это неотрицательное число, квадрат которого равен a, а≥0.
Арифметическийквадратный корень это неотрицательное
число, квадрат которого
равен a, а≥0.
14. Кубический корень из числа – это число, куб которого равен а.
15. Корень n-й степени из числа a – это число, n-я степень которого равна a.
16. Операции с корнями
17.
Корень из произведениянескольких сомножителей
равен произведению
корней из этих
сомножителей
18.
Корень из отношения корнейделимого и делителя
19.
При возведении корня встепень достаточно
возвести в эту степень
подкоренное число
20.
Если увеличить степень корня вn раз и одновременно возвести
в n-ую степень подкоренное
число, то значение корня не
изменится
21.
Если уменьшить степень корня вn раз и одновременно извлечь
корень n-ой степени из
подкоренного числа, то
значение корня не изменится




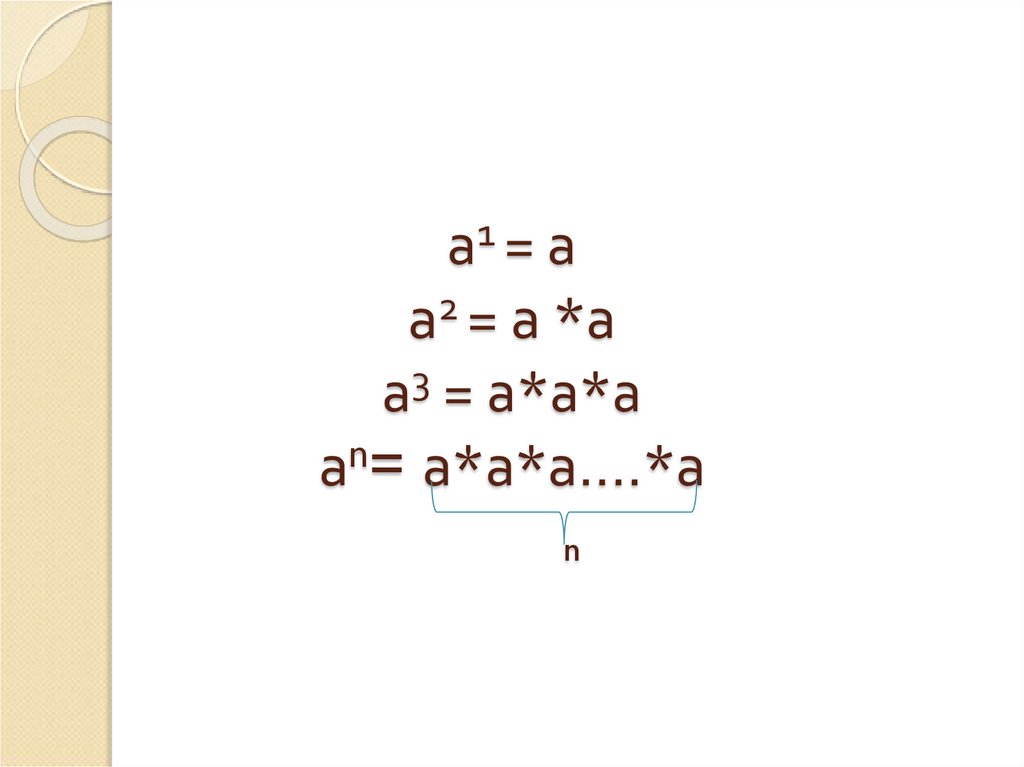





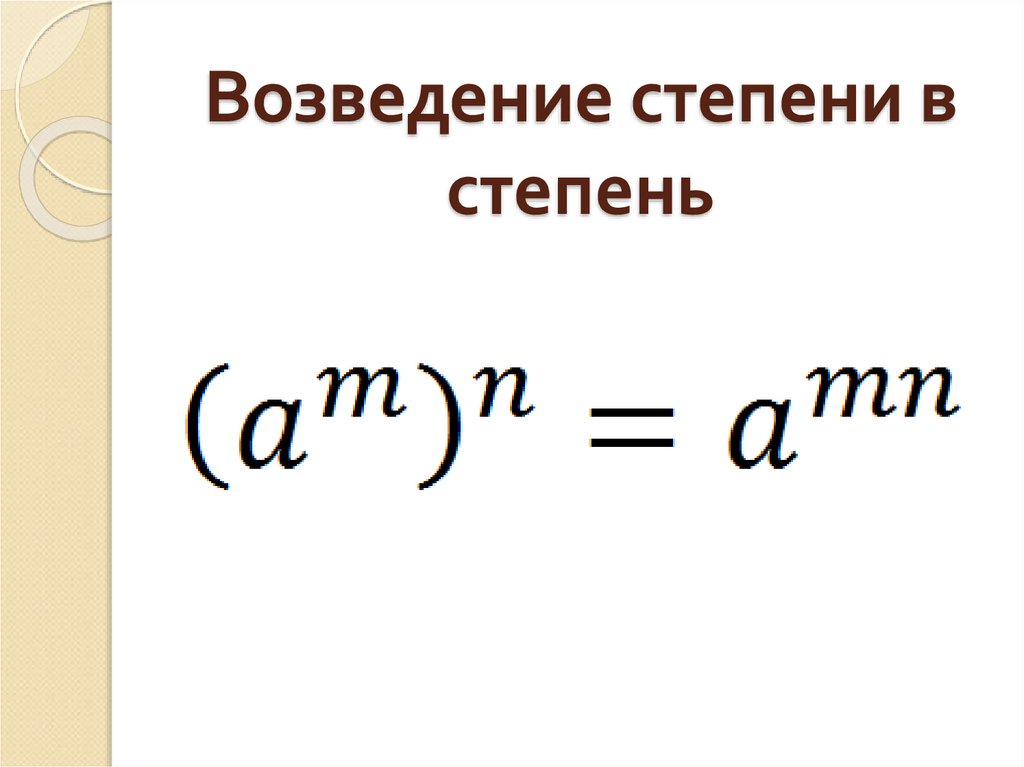





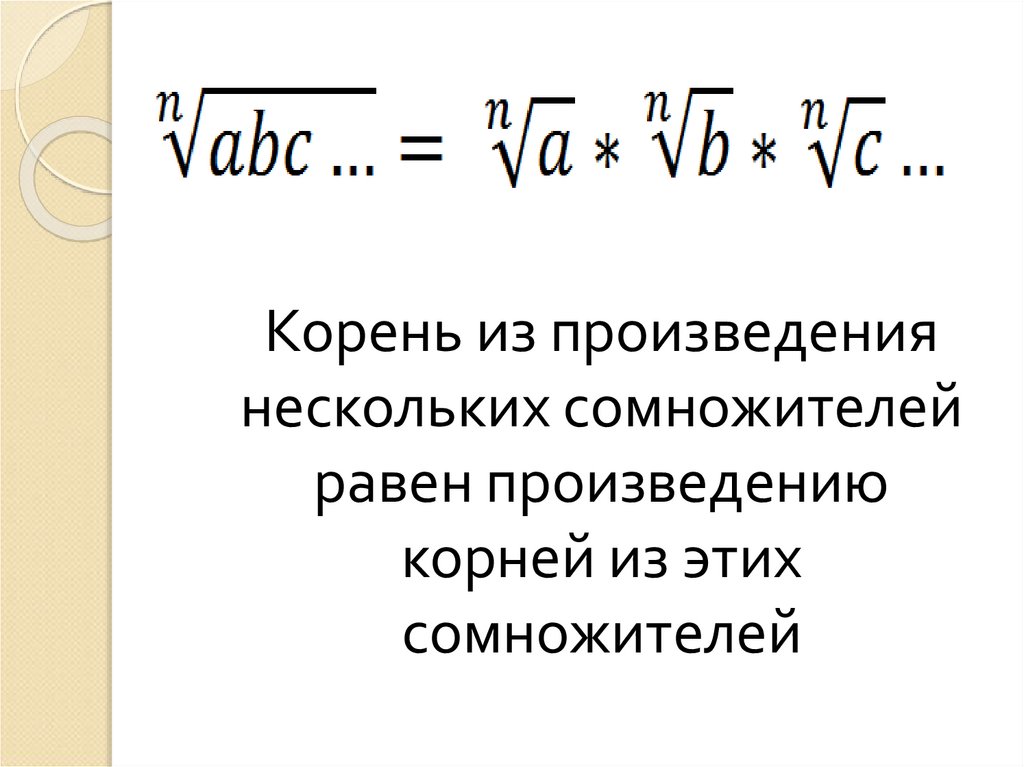




 Математика
Математика








