Похожие презентации:
Сикһеҙ геометрик прогрессия
1. СикўеЎ геометрик прогрессия
Сикһеҙ геометрикпрогрессия
Математика
уҡытыусыһы
Миниязова Л.Ә.
эшләне
2. Формуланы бел
1. Арифметик прогрессияның айырмаһы.2. Арифметик прогрессияның n-сы быуыны формулаһы.
3. Арифметик прогрессияның беренсе n быуындары суммаһы.
4. Геометрик прогрессияның беренсе n быуындары суммаһы.
5. Геометрик прогрессияның n-сы быуыны формулаһы.
6. Арифметик прогрессия быуындарының үҙсәнлеге.
7. Геометрик прогрессия быуындарының үҙсәнлеге.
8. Геометрик прогрессия знаменателе.
9. Кәмей барыусы сикһеҙ геометрик прогрессияның суммаһы.
1. an = a1 + ( n-1)d
5. S = .
2. bn = b1• qn-1
3. Sn .
6. an =
7. bn=
4. Sn =
8. d = an + 1 – an.
9. q =
3. Кљмей барыусы сикўеЎ геометрик прогрессия
Кәмей барыусы сикһеҙ геометрикпрогрессия
Билдәләмә Әгәр геометрик
прогрессияның знаменателе q < 1
булһа, ул кәмей барыусы сикһеҙ
геометрик прогрессия тип атала.
4. СикўеЎ геометрик прогрессия
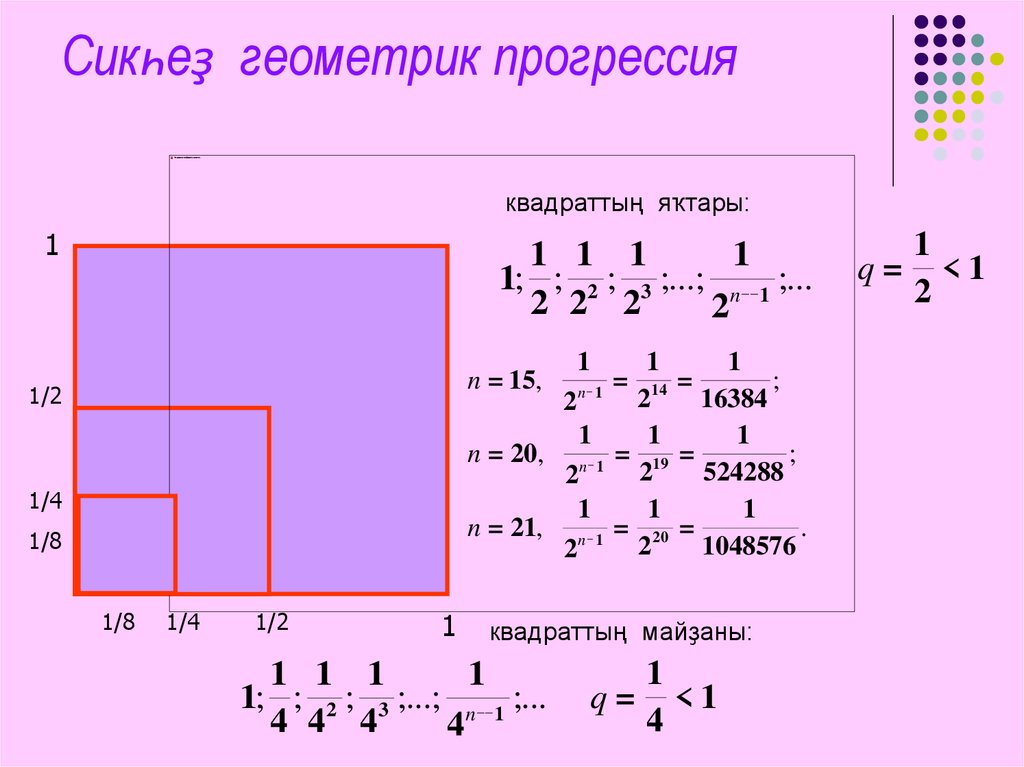
Сикһеҙ геометрик прогрессияквадраттың яҡтары:
1
1 1 1
1
1; ; 2 ; 3 ;...; n __ 1 ;...
2 2 2
2
1
1
1
=
=
;
_
14
n 1
2
16384
2
1
1
1
n = 20, n _ 1 = 19 =
;
2
524288
2
1
1
1
n = 21, n _ 1 = 20 =
.
2
1048576
2
n = 15,
1/2
1/4
1/8
1/8
1/4
1/2
1
квадраттың майҙаны:
1 1 1
1
1; ; 2 ; 3 ;...; n __ 1 ;...
4 4 4
4
1
q= <1
4
1
q= <1
2
5. |q|<1 булћанда,сикўеЎ геометрик прогрессияныҐ суммаўы
|q|<1 булғанда,сикһеҙ геометрикпрогрессияның суммаһы
Билдәләмә : геометрик прогрессияның ,n →∞ сикһеҙ
ҙурайған саҡта, беренсе п быуындары суммаһы ынтылған
һан сикһеҙ геометрик прогрессияның суммаһы тип атала.
b1 (1_ q n )
Sn =
.
_
1 q
q < 1,
q → 0,
n
b1
Sn = _
1 q
_
b1
n
q
.
_
1 q
n → ∞.
b1
S= _
1 q
Шуға күрә
q <1
b1
n
q
→0
_
1 q
6.
q=_
1
;
3
1;
__
1 1
; 2;
33
__
__
n __ 1
1 ( 1)
;...
__
3 ;...;
n 1
3
3
1
1
__ 1
b1 = 1, b2 =
, b3 = , b4 =
3
9
27
__
7. |q|< булћанда, сикўеЎ геометрик прогрессияныҐ суммаўы
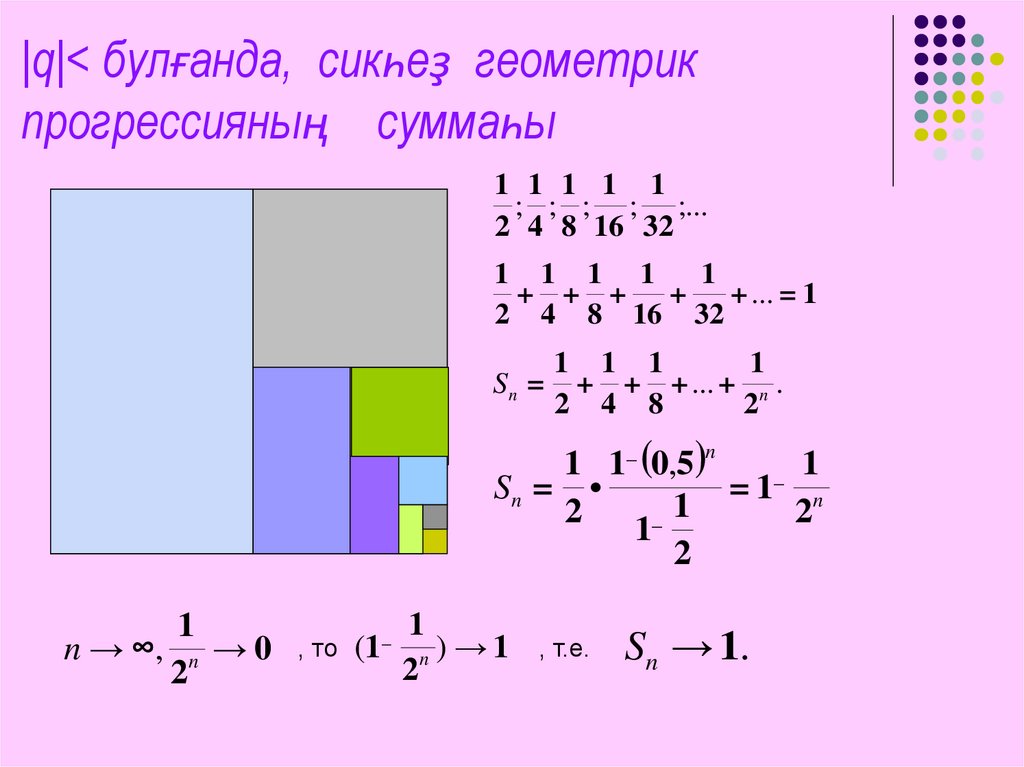
|q|< булғанда, сикһеҙ геометрикпрогрессияның суммаһы
1 1 1 1 1
; ; ; ; ;...
2 4 8 16 32
1 1 1 1
1
+ + + +
+ ... = 1
2 4 8 16 32
1 1 1
1
Sn = + + + ... + n .
2 4 8
2
1 1_ (0,5)n
_ 1
Sn =
=1 n
1
2
2
1_
2
1
n → ∞, n → 0
2
, то
1
(1 n ) → 1
2
_
, т.е.
Sn → 1.
8.
10,(9) сикһеҙ унарлы периодик
кәсерҙе ябай кәсер рәуещендә
яҙырға.
9.
10,(9) сикһеҙ унарлы пероидик
кәсерҙе ябай кәсер рәүешендә
яҙырға.
0, (9 ) =
9
9
9
+ 2 + 3 + ...
10 10 10
1
b1
0,9
0,9
q= ; S= _ ; S= _
=
= 1.
10
1 q
1 0,1 0,9
0, (9) = 1
10. БАРЫЉЫЌЉА ЛА ДЂРЕС ЃСЃН РЂХМЂТ!
БАРЫҒЫҘҒА ЛАДӘРЕС ӨСӨН
РӘХМӘТ!
11. СикўеЎ геометрик прогрессия
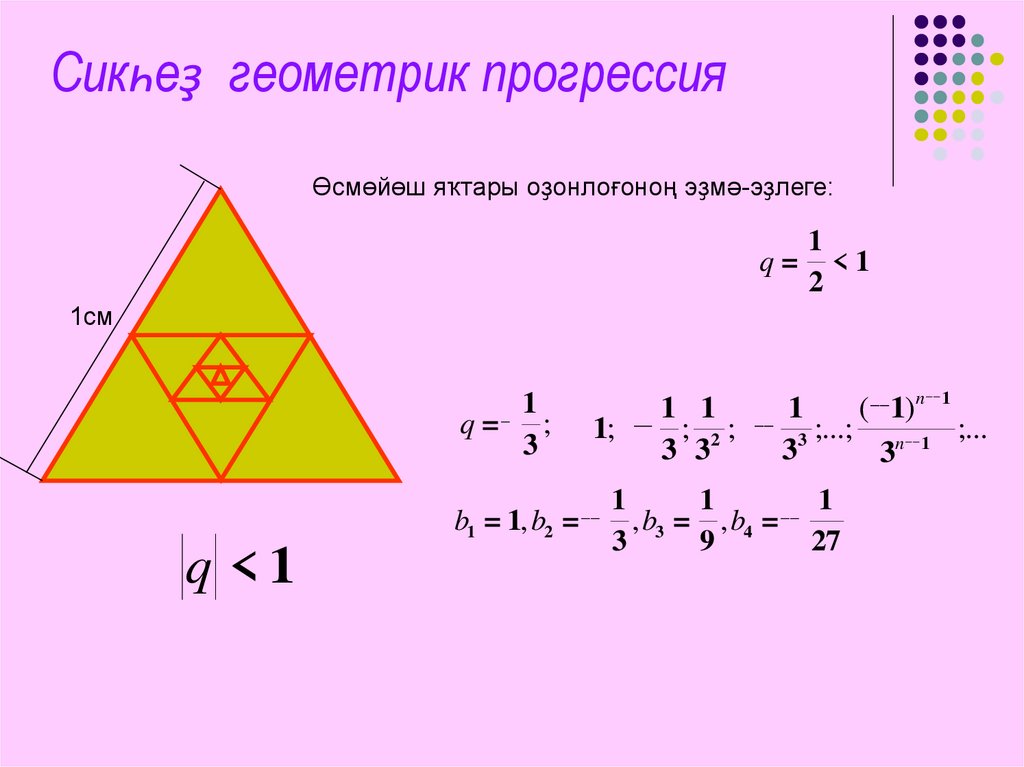
Сикһеҙ геометрик прогрессияӨсмөйөш яҡтары оҙонлоғоноң эҙмә-эҙлеге:
q=
1
<1
2
1см
_ 1
q= ;
3
b1 = 1, b2 =
q <1
1;
__
__
1 1
; ;
3 32
__
__
n __ 1
1
( 1)
;...; n __ 1 ;...
33
3
1
1
__ 1
,b = ,b =
3 3 9 4
27



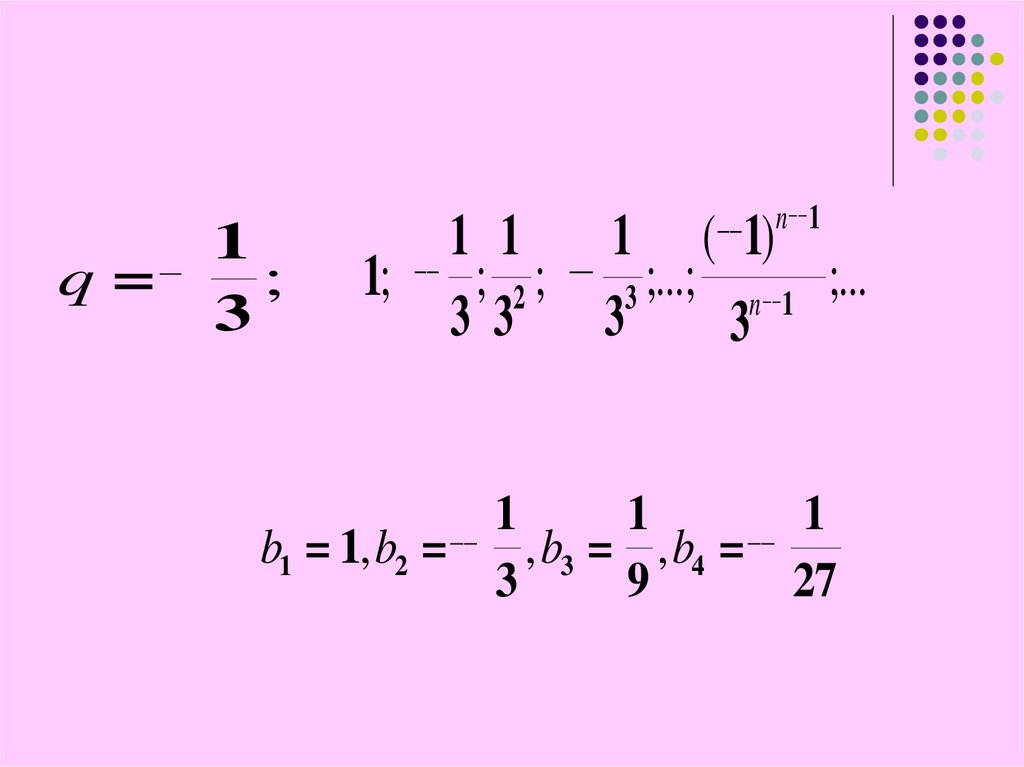



 Математика
Математика