Похожие презентации:
Геометрическая прогрессия. Урок 1
1.
Геометрическаяпрогрессия
Урок 1
2.
Геометрическая прогрессия – это числоваяпоследовательность, первый член которой
отличен от нуля и каждый член, начиная со
второго равен предыдущему умноженному
на одно и тоже число не равное нулю.
b1 , b2 , b3 ,..., bn ,... -геометрическая прогрессия,
если для всех натуральных n выполняется равенство
bn 1 bn q bn 0 q 0
q -знаменатель геометрической прогрессии (число)
3.
Назвать первый член и знаменательгеометрической прогрессии:
4, 2, 1, …
-10, 20, -40, …
-50, 10, -2, …
6, 12, 24, …
4.
Формула n-го членагеометрической прогрессии
bn b1 q
n 1
5.
Доказать, что последовательность,n
заданная формулой bn 3 2 ,
является геометрической прогрессией.
6.
b1 , b2 , b3 ,..., bn ,...-геометрическая прогрессия, если для
всех натуральных n выполняется
равенство
где
q
bn 1 bn q
bn 0 q 0
-знаменатель
геометрической
прогрессии (число)
bn 1
q
bn
7.
Доказать, что последовательность,n
заданная формулой bn 3 2 ,
является геометрической прогрессией.
Решение: bn
3 2 0 при всех n.
n
n 1
bn 1 3 2
2
n
bn
3 2
q 2
-частное не зависит от n
Следовательно
(bn ) - геометрическая
прогрессия
8.
Свойство n-го членагеометрической прогрессии
bn bn 1 q
bn
bn 1
q
bn 1 bn q
b bn 1 bn 1
2
n
bn bn 1 bn 1



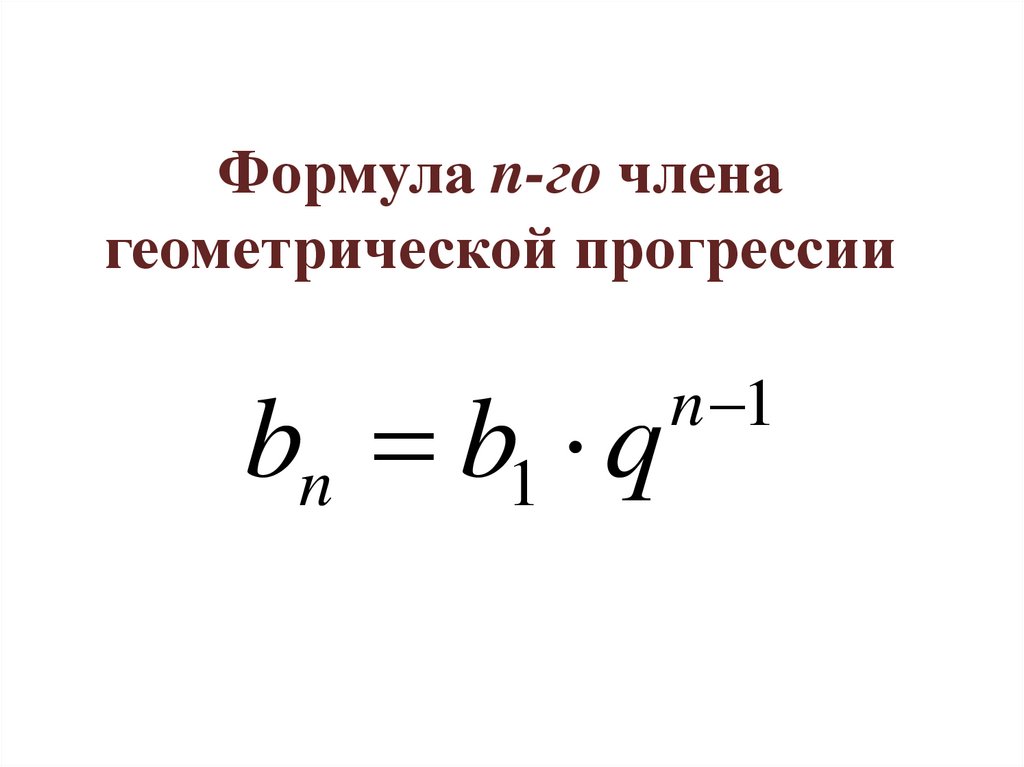




 Математика
Математика








