Похожие презентации:
Геометрическая прогрессия. Урок 3
1.
Геометрическаяпрогрессия
Урок 3
2.
Геометрическая прогрессия – это числоваяпоследовательность, первый член которой
отличен от нуля и каждый член, начиная со
второго равен предыдущему умноженному
на одно и тоже не равное нулю число .
b1 , b2 , b3 ,..., bn ,... -геометрическая прогрессия,
если для всех натуральных n выполняется равенство
bn 1 bn q bn 0 q 0
q -знаменатель геометрической прогрессии (число)
3.
b1 , b2 , b3 ,..., bn ,...-геометрическая прогрессия
bn 1 bn q
bn 1
q
bn
знаменатель
геометрической прогрессии
(число)
q b2 :b1
q b3 :b2
q b4 :b3
4.
Формула n-го членагеометрической прогрессии
bn b1 q
n 1
5.
Свойство n-го членагеометрической прогрессии
b bn 1 bn 1
2
n
6.
Свойство n-го членагеометрической прогрессии
b bn 1 bn 1
2
n
Если все члены прогрессии положительны, то
каждый член геометрической прогрессии,
начиная со второго, равен среднему
геометрическому двух соседних с ним членов.
bn bn 1 bn 1
7.
Сумма n первых членовгеометрической
прогрессии
8.
Сумма n первых членовгеометрической прогрессии
Sn b1 b2 b3 ... bn
S n b1 b1 q b1 q ... b1 q
2
Если
q 1
то
n 1
b1 (1 q )
Sn
1 q
n
9.
1Найти S n , если b1 3, q , n 5
2
n
b
(
1
q
)
1
Решение: S
n
1 q
1
3 1
2
S5
1
1
2
5
3 1 1
32 3 31 2 93
1
32 1 16
2
10.
НайтиS n , если b1 3, q 1, n 5
b1 (1 q )
Sn
1 q
n
Решение:
3 (1 1 )
S5
1 1
5
-дробь не имеет
смысла
Как найти сумму?
11.
Сумма n первых членовгеометрической прогрессии
S n b1 b1 q b1 q ... b1 q
2
Если
то
n 1
q 1
Sn b1 b1 ... b1 b1 n
S n b1 n
12.
НайтиS n , если b1 3, q 1, n 5
Решение:
S n b1 n
S5 3 5 15
13.
Сумма n первых членов геометрическойпрогрессии
b1 (1 q )
Sn
1 q
n
S n b1 n
если
q 1
если
q 1



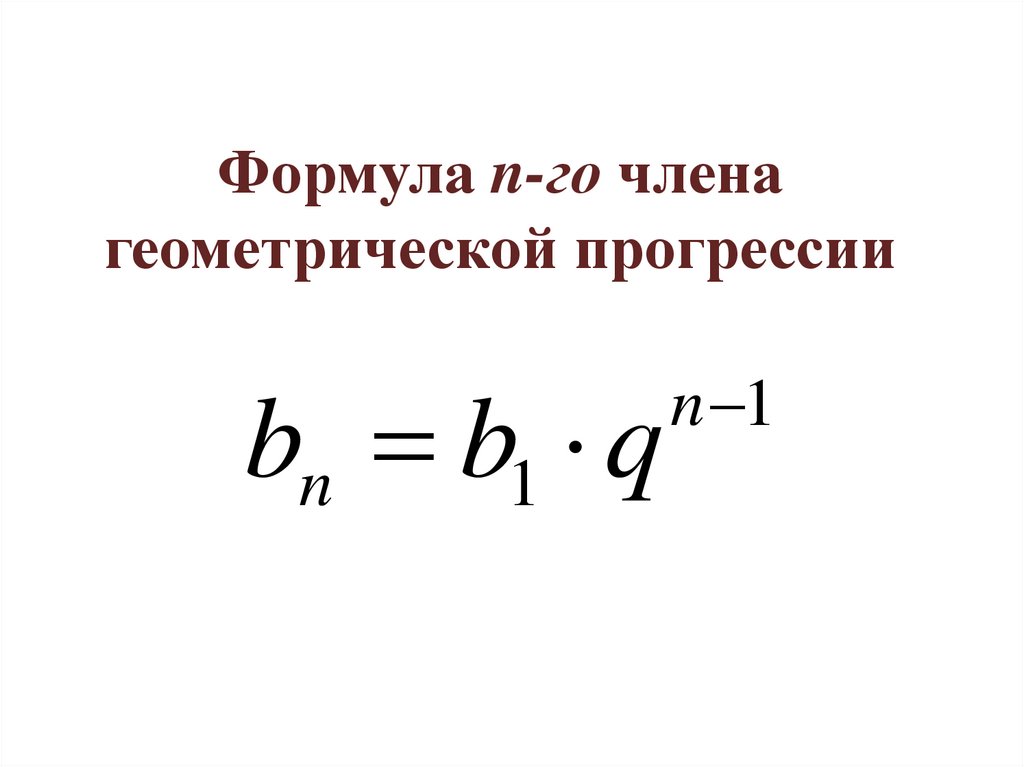
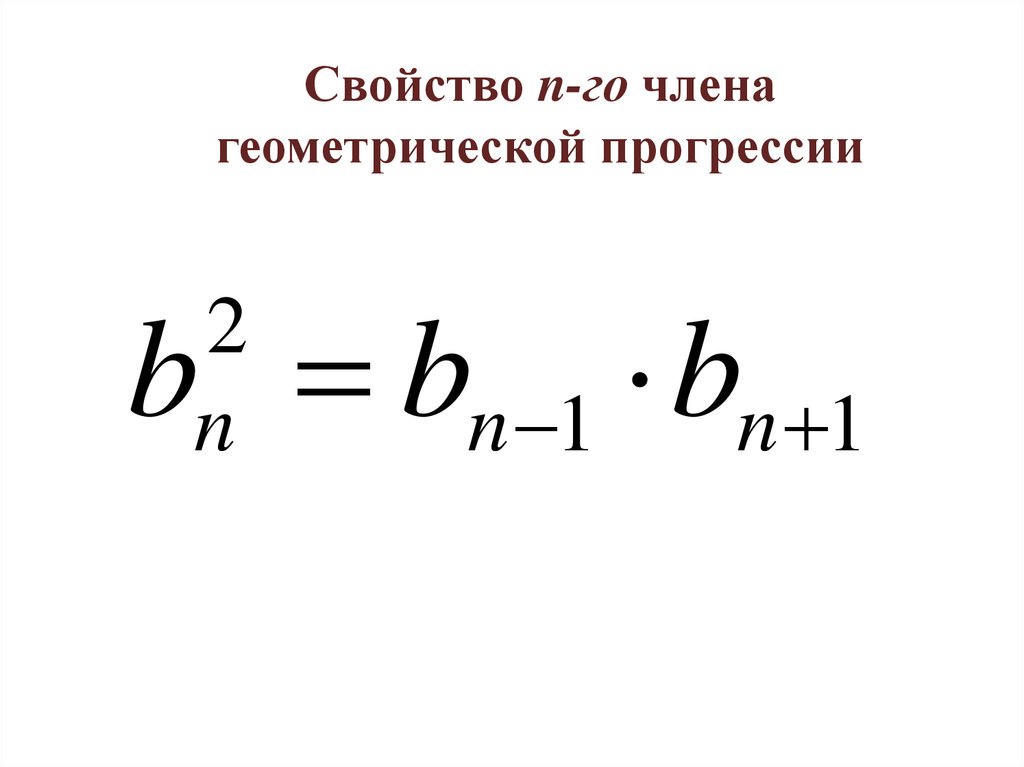



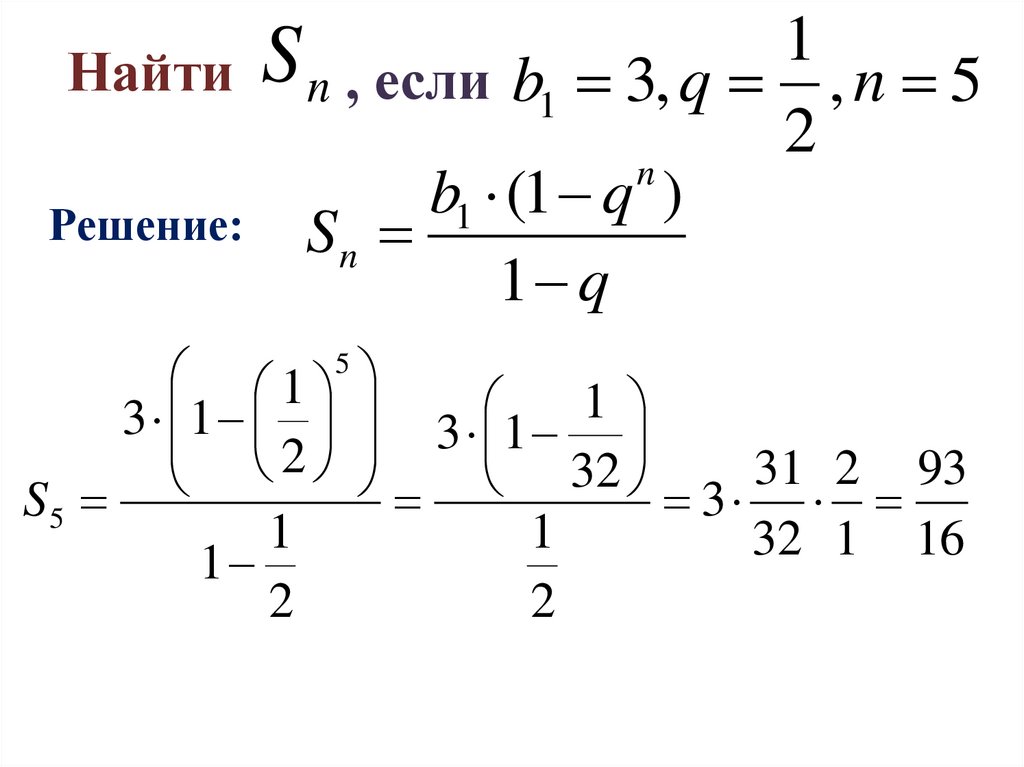




 Математика
Математика








