Похожие презентации:
Применение производной к исследованию функции
1. Применение производной к исследованию функции
2. Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики,
сверх всего того, иумение.
А.Н. Крылов
3. Цель урока:
Практическое применениепроизводной для
исследования функции
4. Область определения функции
- множество всех значений,которые может принимать
её аргумент
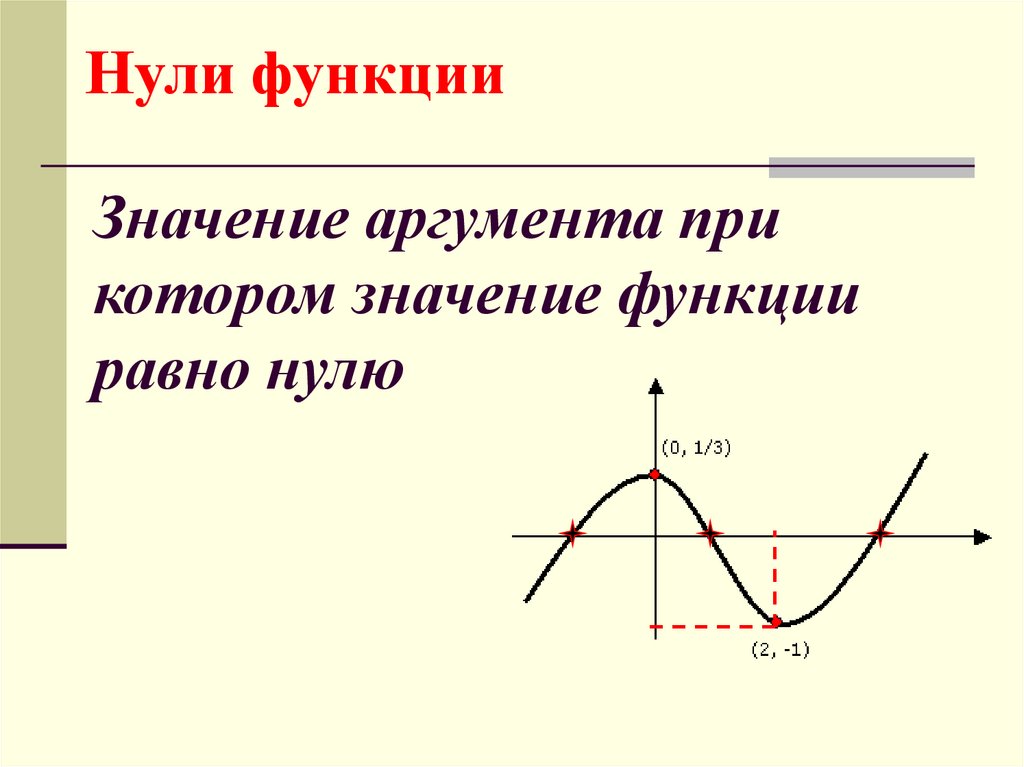
5. Значение аргумента при котором значение функции равно нулю
Нули функцииЗначение аргумента при
котором значение функции
равно нулю
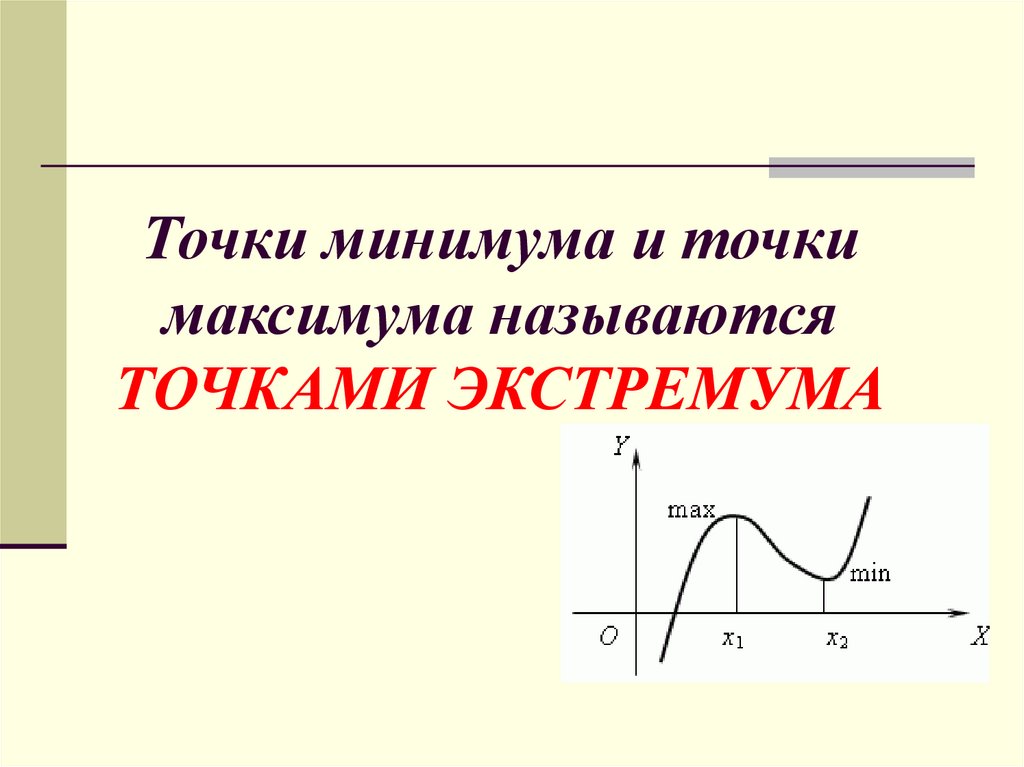
6. Точки минимума и точки максимума называются ТОЧКАМИ ЭКСТРЕМУМА
7. Значение функции в этих точках называется ЭКСТРЕМУМАМИ функции
8. Знаки функции
Определение промежутков накоторых функция
принимает положительные
и отрицательные значения
9. Направления изменений функции
Определение промежутков накоторых функция
возрастает и убывает






 Математика
Математика








