Похожие презентации:
Критические точки: максимумы и минимумы. Схема построения графиков функций
1.
2. Цели:
ЦЕЛИ:повторить алгоритм исследования
непрерывной функции y=f(x) на экстремумы;
используя общую схему находить максимум
и минимум функции.
3. К концу урока мы с вами должны:
К КОНЦУ УРОКА МЫ С ВАМИ ДОЛЖНЫ:знать необходимые и достаточные условия
экстремума;
знать схему построения графиков функций;
уметь находить максимум и минимум
функции
4.
11
2
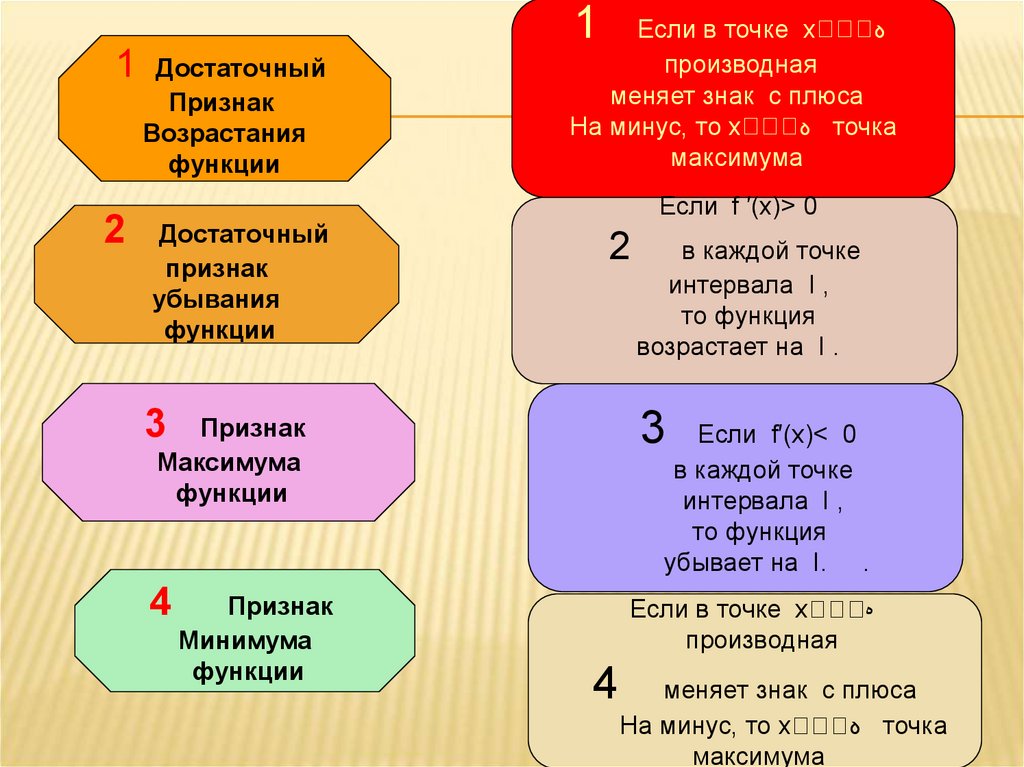
Достаточный
Признак
Возрастания
функции
Достаточный
признак
убывания
функции
Если в точке х
производная
меняет знак с плюса
На минус, то х
точка
максимума
Если f ′(х)> 0
2
3
3
Признак
Максимума
функции
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
Если в точке х
производная
4
меняет знак с плюса
На минус, то х
точка
максимума
5.
1 Если в точке1
2
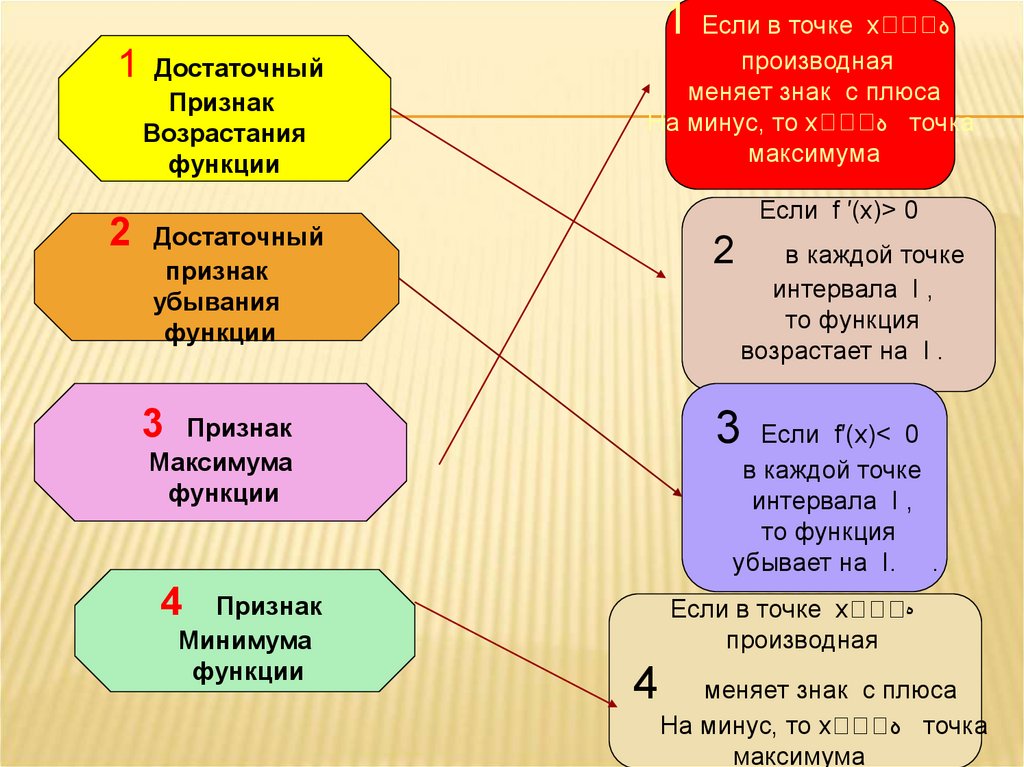
Достаточный
Признак
Возрастания
функции
х
производная
меняет знак с плюса
На минус, то х
точка
максимума
Если f ′(х)> 0
Достаточный
признак
убывания
функции
2
3
3
Признак
Максимума
функции
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если в точке х
производная
4
меняет знак с плюса
На минус, то х
точка
максимума
6.
Кто из вас знаетправила
нахождения
экстремума
Функции?
7.
1.найти область определения функции2. найти производную функции
3. найти точки, в которых выполняется равенство f '(х)=0
4.найти точки, в которых производная не существует
Отметить на координатной прямой все критические точки и
область определения
5. определить знак производной на каждом из промежутков
6. сделать вывод о наличии или отсутствии экстремумов
8.
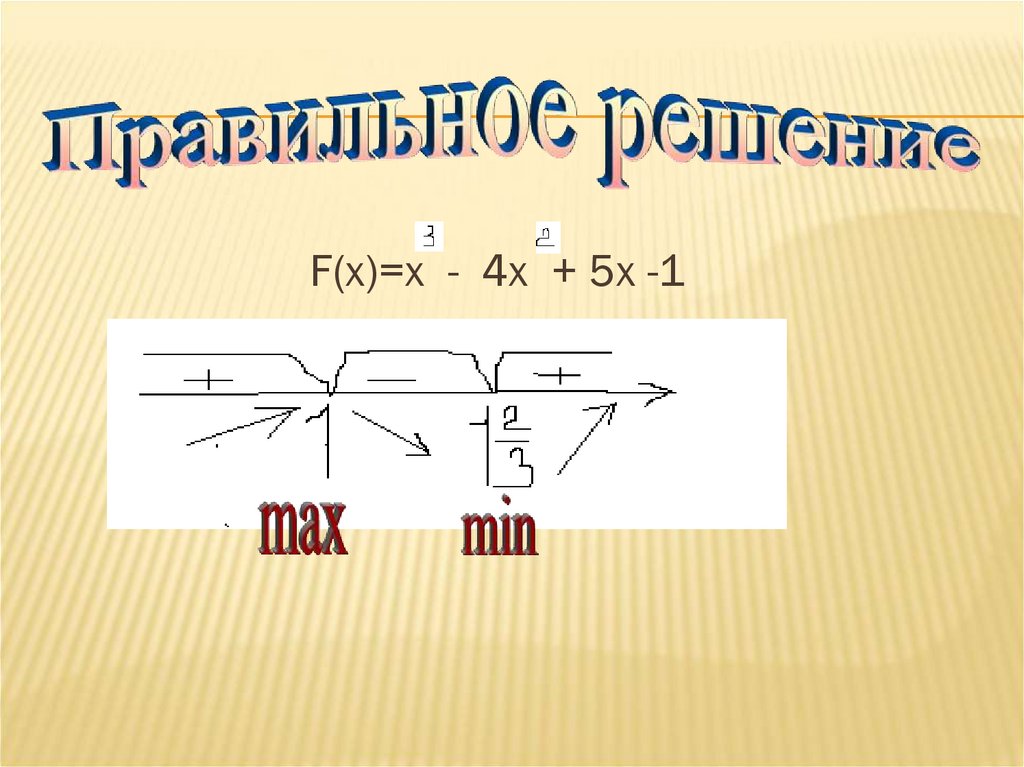
F(х)=х³ - 4 х² + 5х -19.
F(х)=х - 4х + 5х -110.
1. Составить до 10 слайдов о жизни идеятельности Пьера Ферма
2. п.23 №295 (а -в)





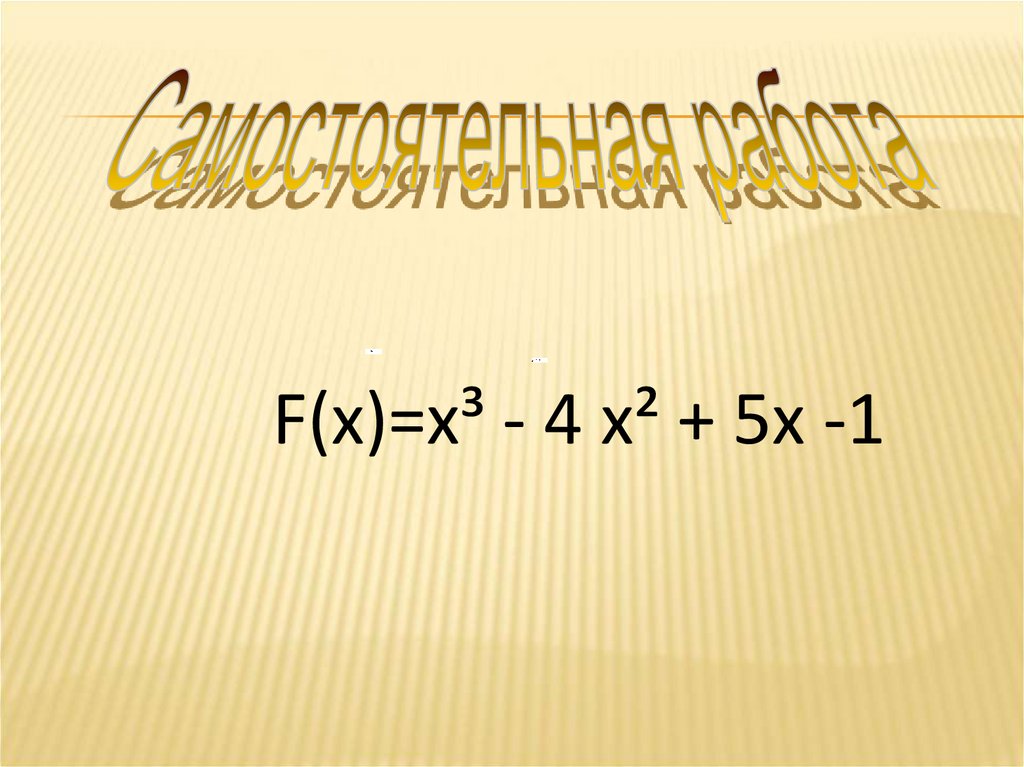


 Математика
Математика








