Поведение функции вблизи критических точек и практическое применение максимума и минимума. Тема №67

1.

Тема урока №67
Поведение функции вблизи
критических точек и практическое
применение максимума и минимума

2.

Цель обучения
11.5.1.22 знать определения критических
точек и точек экстремума функции
Критерии успеха:
- находит критические точки и точки
экстремума
- умеет по графику данной функции
определять точки экстремума

3.

4.

ТЕОРЕМА
Если точка х0 является точкой
экстремума функции f , и в этой точке
существует производная f ', то она
равняется нулю: f'(x0)=0.

5.

Признак максимума функции
Если функция f в точке х0 непрерывна и на интервале
(а, х0) f '(x) > 0 , а на интервале (х0,b) f '(x)< 0, то точка
х0 является точкой максимума функции f.
Признак минимума функции
Если функция f в точке х0 непрерывна и на интервале
(а, х0) f '(x)< 0, а на интервале (х0,b) f '(x) > 0, то точка
х0 является точкой минимума функции f.
f'(x) + х1
f(x)
max
-
х2
min
+
х3
max
-

6.

Признак максимума функции
(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
+
0
-
f (x)
max
fmax(x) = f (x0)
Признак минимума функции
(а;b)
(a; x0)
x0
(x0;b)
f ‘ (x)
-
0
+
f (x)
min
fmin(x) = f (x0)

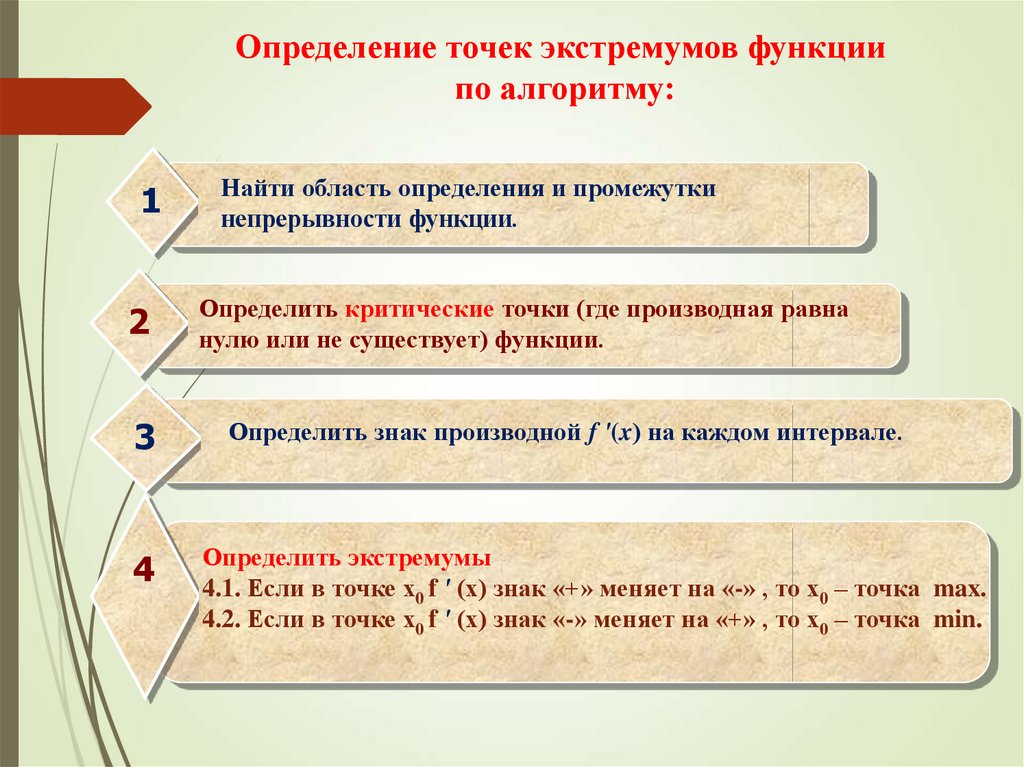
7. Определение точек экстремумов функции по алгоритму:

1
2
3
4
Найти область определения и промежутки
непрерывности функции.
Определить критические точки (где производная равна
нулю или не существует) функции.
Определить знак производной f '(x) на каждом интервале.
Определить экстремумы
4.1. Если в точке х0 f ' (x) знак «+» меняет на «-» , то х0 – точка max.
4.2. Если в точке х0 f ' (x) знак «-» меняет на «+» , то х0 – точка min.

8.

Фронтальная работа
1. Определить точки экстремумов функции и
значения функции в точках экстремума, т.е. сами
экстремумы
a) у 7 х 56 х 8; b) у х 2 х 3.
2
2

9.

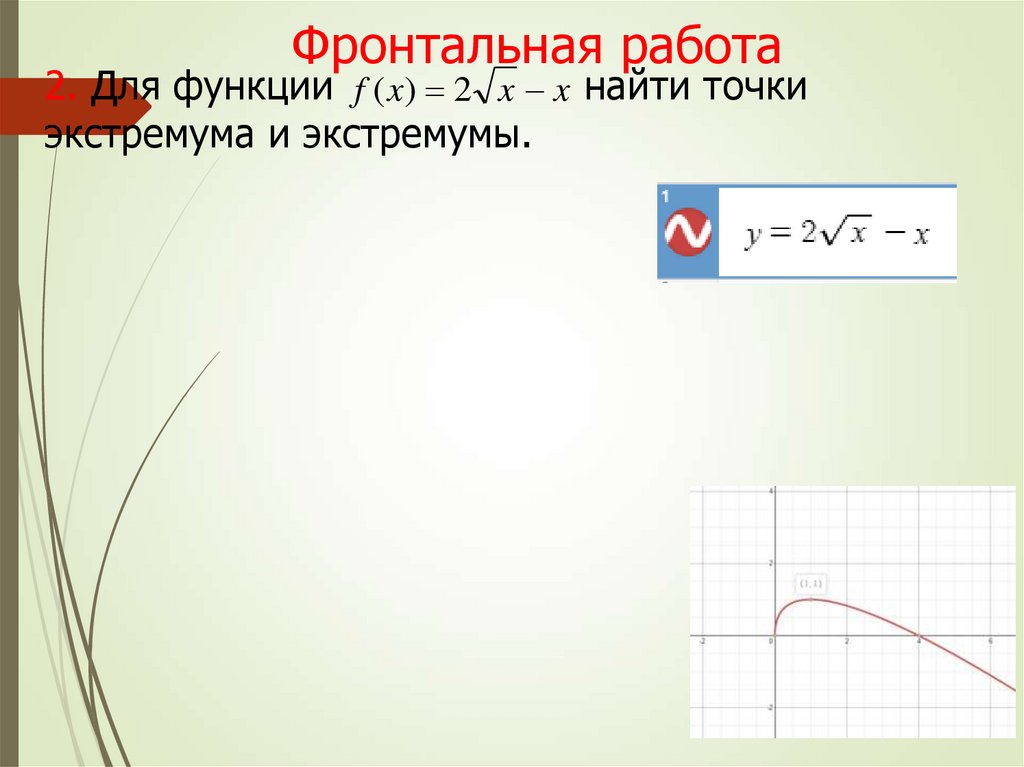
Фронтальная работа
2. Для функции f ( x) 2 x x найти точки
экстремума и экстремумы.

10.

Фронтальная работа
3. Для функции взяли производную:
f ( x) x 2 1 x 2 9 x 2 16 .
Найдите суммарную длину промежутков
убывания функции.

11.

ДЗ
Определить экстремумы функции и значения
функции в точках экстремума
2
3
2
1) у 4 х х ;
2) у х 6 х 9 х;
1
х
х
3) у 2 х 3; 4) у х.
3 2
х
3
2

12.

1) у 4 х х ;
2
xmax 2
ymax 4

13.

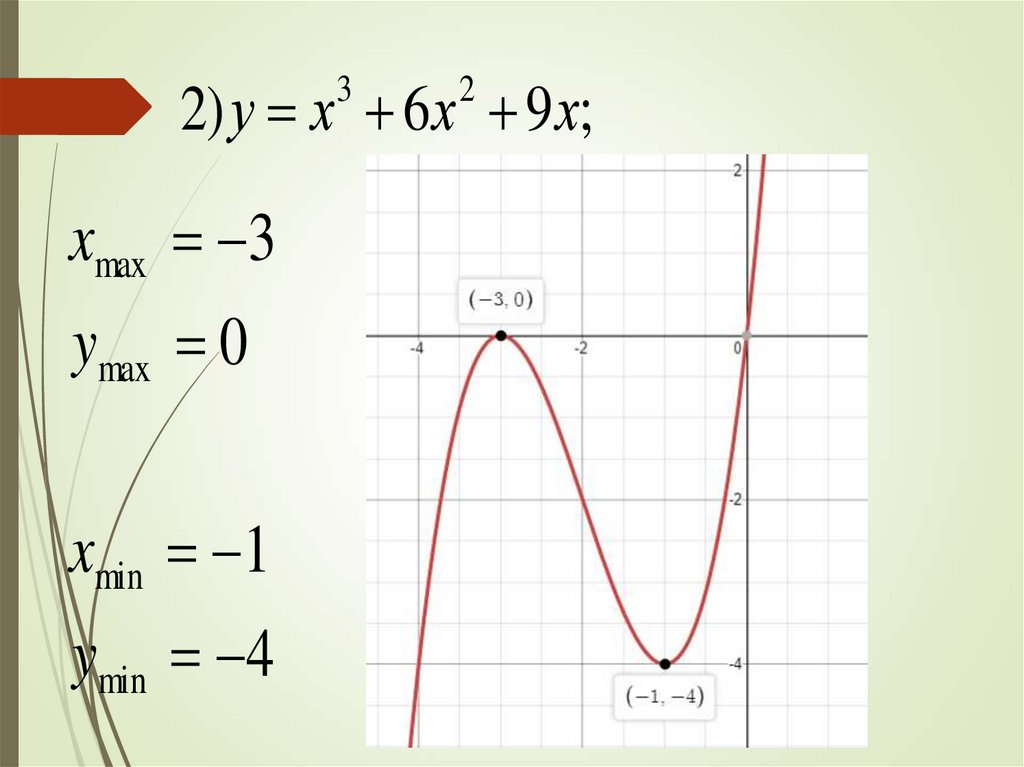
2) у х 6 х 9 х;
3
xmax 3
ymax 0
xmin 1
ymin 4
2

14.

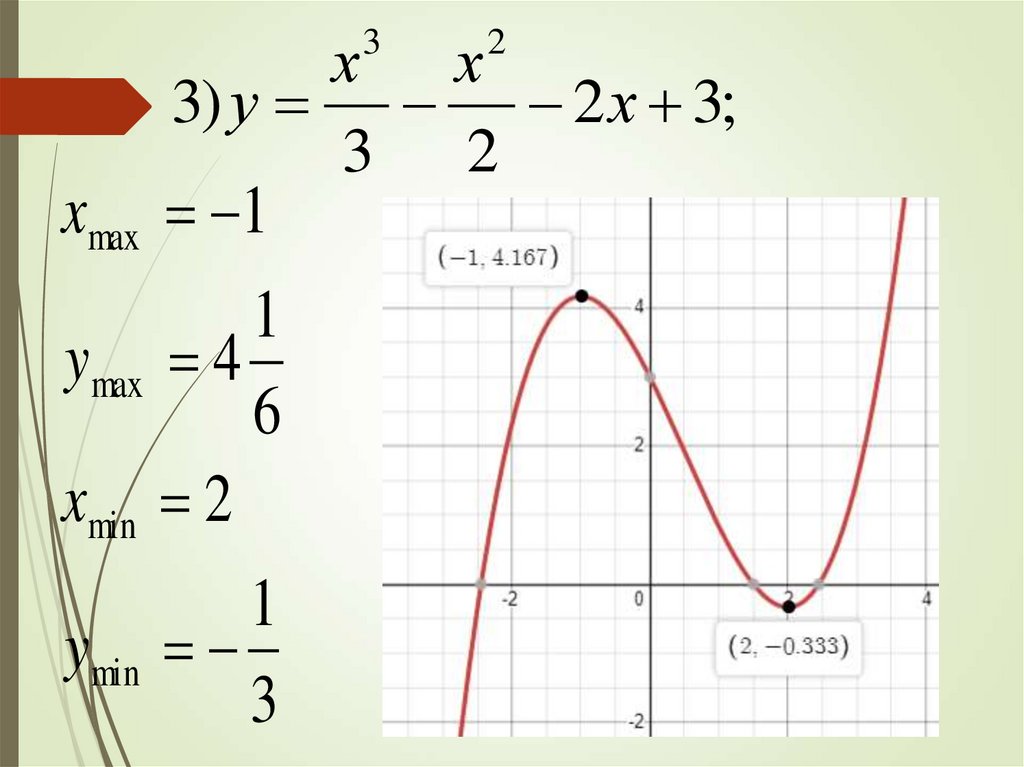
х
х
3) у 2 х 3;
3 2
3
xmax 1
1
ymax 4
6
xmin 2
ymin
1
3
2

15.

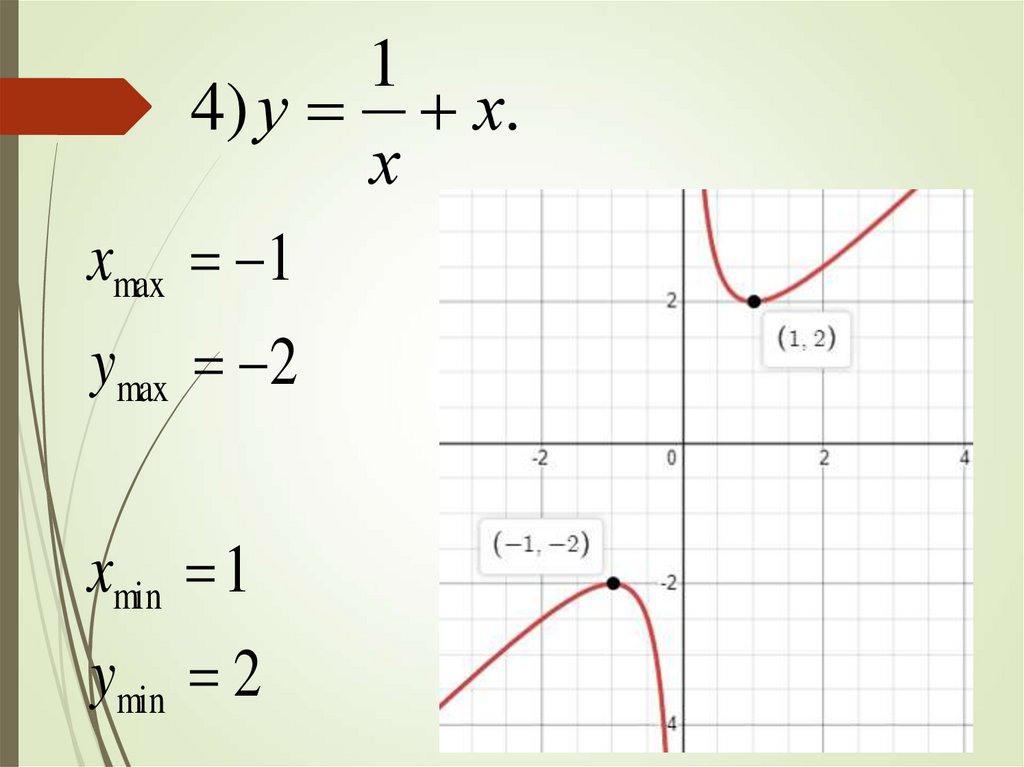
xmax
1
4) у х.
х
1
ymax 2
xmin 1
ymin 2