Неопределённый интеграл

1. ТЕМА 7. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

2. ПервоÓбразная:

Задача дифференциального исчисления
(предыдущая тема): по данной функции
найти её производную.
Задача интегрального исчисления: найти
функцию, зная её производную.
Функция F(x) называется первообразной для
функции f(x) на заданном промежутке,
если для любого х из этого промежутка
справедливо равенство
Fʹ(x) = f(x)

3. Пример:

Найти первообразные для функций:
1)
f ( x ) 3 x F ( x) x
2)
1 6
f ( x) x F ( x) x
6
3)
2
5
3
x R,
x 3x
3
2
1 6
x R, x x 5
6
1
f ( x)
F ( x) ln x
x
x R \ 0
1
f ( x) , x 0; F ( x) ln x,
x
1
f ( x) , x ; 0 F ( x) ln( x),
x
1
ln x
x
ln( x)
1
1
1
x
x

4.

Для всякой ли функции f(x) существует
первообразная?
Теорема.
Если
функция
непрерывна
на
какомнибудь промежутке, то она
имеет на
нём
первообразную.

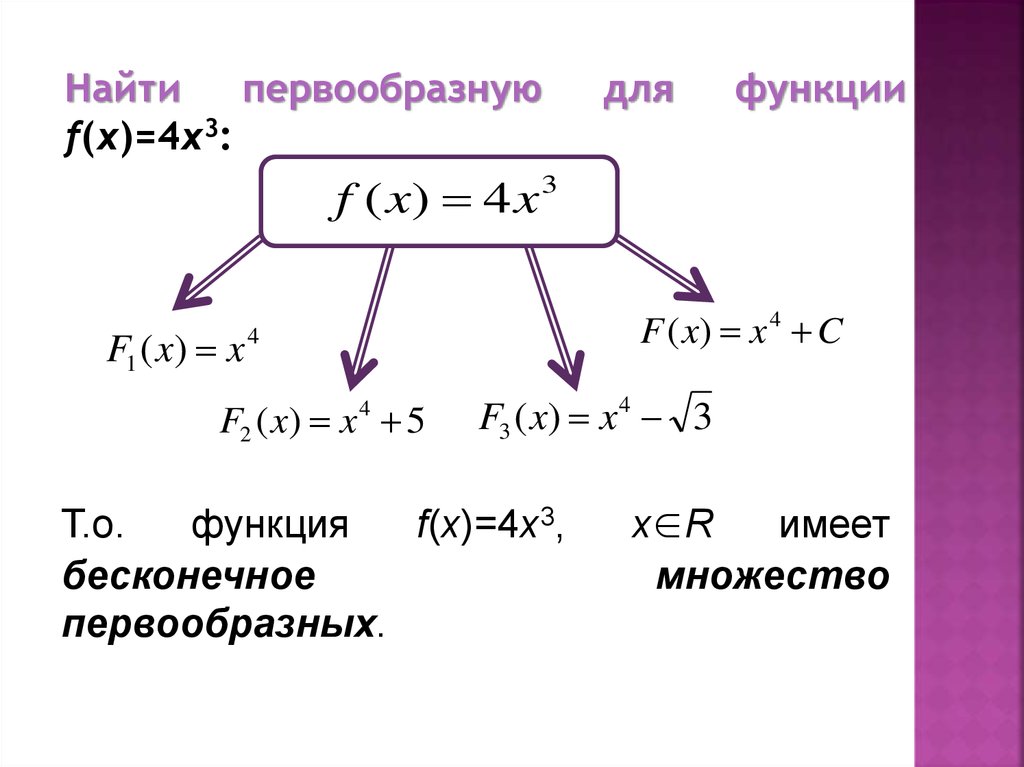
5.

Найти
первообразную
f(x)=4x3:
для
функции
f ( x) 4 x 3
F1 ( x) x
F ( x) x 4 C
4
F2 ( x) x 5
4
F3 ( x) x 4 3
Т.о.
функция
f(x)=4x3,
бесконечное
первообразных.
х∈R
имеет
множество

6.

Теорема.
Если
функция
F(x)
является
первообразной для функции f(x) на
некотором промежутке, то множество
всех первообразных этой функции имеет
вид F(x)+C, где C∈R.
y
Геометрически:
Первообразная F(x) + C
представляет
собой
семейство
кривых
интегральных,
получаемых из каждой из
них
параллельным
переносом вдоль оси ОУ.
интегральная кривая
С
0
x

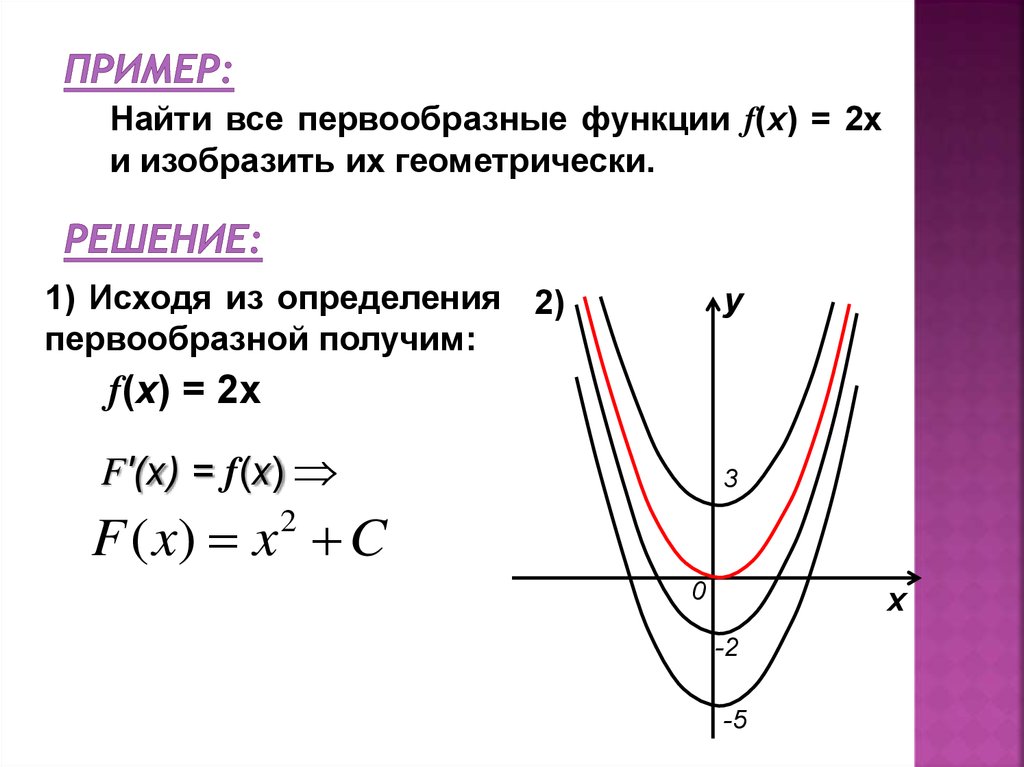
7. Пример:

Найти все первообразные функции f(x) = 2x
и изобразить их геометрически.
1) Исходя из определения 2)
первообразной получим:
y
f(x) = 2x
Fʹ(x) = f(x)
3
F ( x) x C
2
0
x
-2
-5

8. Неопределённый интеграл:

Множество
всех
первообразных
F(x)+C функции f(x) на некотором
промежутке
называется
неопределённым
интегралом
и
обозначается символом f ( x) dx , т.е
f ( x) dx F ( x) C

9.

f ( x) dx F ( x) C
f (x)
f ( x) dx
х
F(x)+C
С
– подынтегральная функция;
– подынтегральное
– переменная
выражение;
интегрирования;
- знак неопределённого интеграла;
– множество
всех первообразных;
– постоянная
интегрирования.
Процесс нахождения первообразной функции
называется интегрированием, а раздел
математики
–
интегральным
исчислением.

10. Свойства неопределённого интеграла

10.
Дифференциал от неопределённого
интеграла
равен
подынтегральному
выражению,
а
производная
неопределённого
интеграла
равна
подынтегральной функции:
d
f ( x) dx f ( x) dx, f ( x) dx f ( x)

11.

Доказательство:
d
f ( x) dx d F ( x) C d F ( x) d C F ( x) dx f ( x) dx
f ( x) dx (F ( x) C) F ( x) C f ( x)
То есть правильность интегрирования
проверяется дифференцированием.
Равенство:
3x
верно, так как
x
3
2
4 dx x 4 x C
3
4 x C 3x 4
2

12.

20.
Неопределённый
интеграл
от
дифференциала некоторой функции равен
этой
функции
плюс
произвольная
постоянная, т.е.:
d
F
(
x
)
F
(
x
)
C
Доказательство:
d F ( x) F x dx f ( x) dx F x C

13.

30.
Неопределённый
интеграл
от
алгебраической суммы (разности) двух
или
нескольких
функций
равен
алгебраической суммы (разности) их
интегралов, т.е.:
f
(
x
)
g
(
x
)
dx
f
(
x
)
dx
g
(
x
)
dx
Доказательство:
свойством 10.
воспользуемся
f ( x) g ( x) dx f ( x) g ( x)
f ( x) dx g ( x) dx f ( x) dx g ( x) dx f ( x) g ( x)

14.

40.
Постоянный
множитель
выносить за знак интеграла, т.е
можно
a
f
(
x
)
dx
a
f
(
x
)
dx
,
a
0
Доказательство:воспользуемся свойством 10:
a f ( x) dx a f ( x)
a f ( x) dx a f ( x) dx a f ( x)

15. Таблица неопределенных интегралов

Пользуясь тем, что интегрирование –
процесс обратный дифференцированию, можно
получить таблицу основных интегралов путем
обращения формул дифференцирования и
использования
свойств
неопределенного
интеграла
Отметим, что в таблице основных
интегралов переменная интегрирования u
может обозначать как независимую переменную,
так и функцию от независимой переменой.

16. Таблица неопределенных интегралов (для замены переменной х на u)

17. Таблица неопределенных интегралов

1. dx x C .
a 1
x
2. x dx
C, (a 1) .
a 1
dx
3. ln x C .
x
x
a
4. a x dx C .
ln a
a
5.
x
x
e
dx
e
C .
6. sin xdx cos x C .
7. cos xdx sin x C .
dx
8. 2 ctgx C .
sin x
dx
9. 2 tgx C .
cos x
dx
10. 2 arctgx C .
1 x

18. Таблица неопределенных интегралов

11.
dx
arcsin x C .
1 x 2
dx
1
x
12. 2 2 arctg C .
a
a
a x
13.
14.
15.
dx
a2 x2
arcsin
x
C ..
a
dx
1
x a
ln
C
2
2
2a x a
x a
dx
1
a x
ln
a 2 x 2 2a a x C .
16.
dx
x2 a
ln x x 2 a C .

19. Основные методы интегрирования

Непосредственным
интегрированием
называется такой метод вычисления
интегралов,
при
котором
они
сводятся
к
табличным
путём
применения к ним основных свойств
неопределённого интеграла. При этом
подынтегральную
функцию
обычно
соответствующим
образом
преобразуют.

20. Метод интегрирования подстановкой

заключается во введении новой
переменной интегрирования (т.е. подстановки ). При этом заданный интеграл
приводится к новому интегралу, который является табличным или к нему
сводящимся (в случае удачной подстановки)
Пусть требуется вычислить интеграл f ( x)dx Сделаем подстановку x (t ) где (t )
функция имеющая непрерывную производную тогда dx (t )dt
/
На основании инвариантности формулы интегрирования неопределенного
интеграла получим формулу интегрирования подстановкой
f ( x)dx f ( (t ) / (t )dt )
Эта формула называется формулой интегрирования заменой переменой в
неопределенном интеграле. После нахождения интеграла правой части этого
равенства следует перейти от новой переменной интегрирования t к переменой x

21. Метод интегрирования по частям

Формула
udv u v vdu
u u ( x) и v v ( x ) функции имеющие
где
непрерывные производные
называется формулой интегрирования по частям. Она
дает возможность свести вычисление интеграла udv к
вычислению интеграла vdu . Что значительно проще
вычисления исходного интеграла.
Вообще сущность метода интегрирования по частям в том
что подынтегральное выражение заданного интеграла
представляется каким либо образом в виде произведения
двух сомножителей dv и u после этого используется
непосредственно формула интегрирования по частям.

22. Теоремы

Корень многочлена – такое значение x0переменой x0 при
котором многочлен обращается в нуль
Если x1корень многочлена Pn ( x) то многочлен делится без
остатка на x x1
Pn 1 ( x) - Многочлен n 1 степени
(основная теорема)
Всякий многочлен n ой имеет по крайней мере один корень
действительный или комплексный x
Всякий многочлен можно представить в виде:
Pn ( x) a0 ( x x1 )( x x2 )( x x3 )

23. Интегрирование рациональных выражений

Рассмотрим способы нахождения интегралов вида
P( x)
Q( x)dx где
Q ( x) и P ( x ) некоторые многочлены от
переменой x
Простейшие случаи относятся к табличным таким как
1.
2.
n 1
x
n
x
dx n 1 C
dx
x
dx
1
x
arctg c
2
2
3. a x
a
a
dx
1
x
x a
C
4. 2 2 ln c
a x
2a a
x a

24. Пример 1. Вычислить интеграл

2 x
2 x
4
4
3 sin x 5e x dx
3 sin x 5e x dx 2 x 4 dx 3 sin x dx 5e x dx
x 4 1
2 x dx 3 sin x dx 5 e dx 2
C1 3 cos x C2 5 e x C3
4 1
4
x
2 5
x 3 cos x 5e x C ,
5
C C1 C 2 C3

25. Пример 2. Вычислить интеграл

2x x
3 x dx
1
2x x
3
6
2
dx
2
x
x
x
dx
2
x
3x
dx
1
13
6
7
x
12 6 13
12 2 6
2
C x C x x C
13
13
13
6

26. Пример 3. Вычислить интеграл

2 x4
x dx
2 x4
2 x4
2
3
dx
dx
dx
x
x
x x
x
dx
4
dx
x
2 x 3 dx 2 ln x C
x
4

27. Пример 4. Вычислить интеграл

3
x
4 dx
2x
x
48
3 4 dx 3 16 dx 48 dx ln 48 C
x
2x
x
x
x

28. Пример 5. Вычислить интеграл

dx
sin 2 x cos 2 x
dx
1
sin 2 x cos 2 x
sin 2 x cos 2 x sin 2 x cos 2 x dx sin 2 x cos 2 x dx
sin 2 x
cos 2 x
1
1
dx
2
2
2 dx
2
2
2
cos x sin x
sin x cos x sin x cos x
dx
dx
2 tan x cot x C
2
cos x
sin x

29. Пример 6. Вычислить интеграл

dx
25 4 x 2
dx
25 4 x 2
dx
1
dx
2
4 5
25
2
4
x
x2
4
2
1 2
2x
1
2x
arctan
C arctan
C
4 5
5
10
5

30. Пример 7. Вычислить интеграл

x2
x 2 1 dx
x2 1
x2
x2 1 1
1
x 2 1 dx x 2 1 dx x 2 1 x 2 1 dx
1
dx
1 2
x arctan x C
dx dx 2
x 1
x 1

31. Пример 8. Вычислить интеграл

2
cot
x dx
2
2
2
cos
x
1
sin
x
1
sin
x
2
cot x dx sin 2 x dx sin 2 x dx sin 2 x sin 2 x dx
dx
1
2 1 dx 2 dx cot x x C
sin x
sin x

32. Пример 9. Вычислить интеграл

x 3 3x 2 3x 1
dx
2
x x
x 3 3x 2 3x 1
x3 1 3x x 1
dx
x 2 x dx
x x 1
x 1 x 2 x 1 3x x 1
x 1 x 2 2 x 1
dx
dx
x x 1
x x 1
x 2 2x 1
x 2 2x 1
dx
dx dx x dx 2 dx
x
x x
x
x
x2
2 x ln x C
2

33. Пример 10. Вычислить интеграл

1 2x2
x 2 1 x 2 dx
1 x2
1 2x2
1 x2 x2
x2
x 2 1 x 2 dx x 2 1 x 2 dx x2 1 x 2 x 2 1 x 2
dx
1
dx
dx
dx
1
2
2
dx 2
x dx
2
2
2
x
1 x
1 x
x 1 x
x 1
1
arctan x C arctan x C
1
x