Похожие презентации:
Четырехугольники» и систематизировать свои знания. Электронное пособие по геометрии. 2012 год
1. Пособие поможет учащимся наглядно представить изучаемый материал по теме: «Четырехугольники» и систематизировать свои знания
Электронное пособие погеометрии
2012
год
Пособие поможет учащимся наглядно представить
изучаемый материал по теме: «Четырехугольники»
и систематизировать свои знания
Разработал ученик 11 «А» класса МБОУ СОШ №15
г.Королёва
Челыхов Михаил под руководством учителей
Диановой В.А. и Моисеевой В.И.
2. Четырёхугольники
ЧЕТЫРЁХУГОЛЬНИКИ
Виды четырёхугольников
Параллелогр
амм
Произвольный
четырёхугольн
ик
Прямоугольн
ик
Квадр
ат
Трапеция
Ромб
Равнобок
ая
Прямоуголь
ная
3. Произвольный четырёхугольник
Сумма внутреннихуглов равна 360 .
Площадь
(через диагонали
и
угол
между
ними):
S=
d
2
d
1
.
4. Четырехугольник , описанный около окружности
cb
d
r
a
Четырехугольник можно
описать около окружности,
если суммы
противолежащих сторон
равны: a + c=b +
d.
Если четырехугольник
описан около окружности, то
суммы противолежащих
сторон равны.
Площадь: S=pr, где p=(a + b + c + d)/2
(полупериметр),
r –радиус вписанной окружности.
Формула S = pr справедлива для любого
многоугольника, описанного около окружности.
5. Четырехугольник, вписанный в окружность
Четырехугольник можно вписать вокружность, если сумма
противолежащих углов равна
180 .
c
b
d2
d1
d
a
Если четырехугольник вписан в
окружность, то суммы
противолежащих
углов равна 180 .
Теорема Птолемея
Сумма произведений
противолежащих сторон равна
произведению диагоналей:
а∙c + b ∙ d = d1d2
c
d
b
a
Площадь (Формула Геррона)
где p =
(полупериметр).
6. Параллелограмм
Определение: параллелограммом называетсячетырехугольник, у которого
противоположные стороны попарно параллельны.
Свойства
параллелограмма
Диагонали
точкой
пересечения
делятся пополам.
Противолежа
щие стороны
попарно
равны.
Противолежащие
углы попарно
равны
Сумма углов,
прилежащих к любой
стороне, равна
.
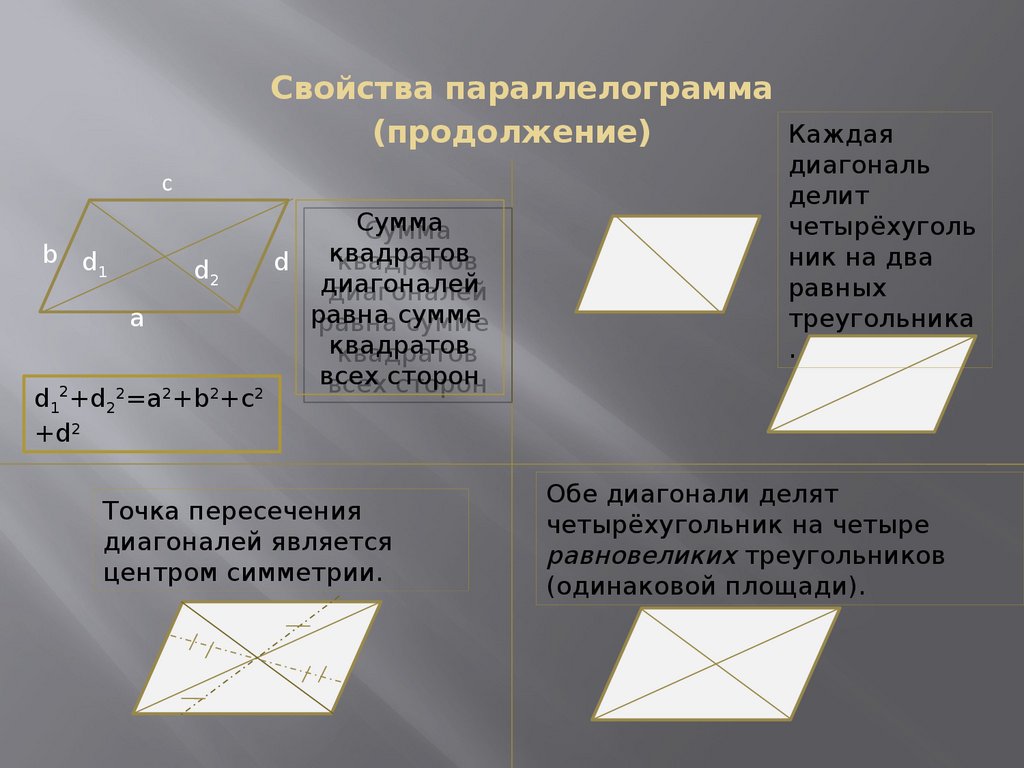
7. Свойства параллелограмма (продолжение)
Каждаяc
b d
1
d2
a
d12+d22=a2+b2+c2
+d2
Сумма
Сумма
квадратов
квадратов
d
диагоналей
диагоналей
равна
равнасумме
сумме
квадратов
квадратов
всех
всехсторон
сторон
Точка пересечения
диагоналей является
центром симметрии.
диагональ
делит
четырёхуголь
ник на два
равных
треугольника
.
Обе диагонали делят
четырёхугольник на четыре
равновеликих треугольников
(одинаковой площади).
8. Признаки параллелограмма.
Если в четырёхугольнике двестороны равны и параллельны, то
этот четырёхугольник ―
параллелограмм.
Если в четырёхугольнике
противоположные стороны попарно
равны, то этот четырёхугольник ―
параллелограмм.
Если в четырёхугольнике диагонали
пересекаются и точкой пересечения
делятся пополам, то этот
четырёхугольник ― параллелограмм.
9. Площадь параллелограмма
bh
ha
b
a
b
Через сторону и опущенную на
неё высоту
Площадь параллелограмма равна
произведению основания на высоту.
S=aha=b hb
Через две прилежащие стороны и угол
между ними
Площадь параллелограмма равна
произведению его смежных сторон на
синус угла между ними S=a b∙sin
a
d1
d2
Через диагонали и угол между
ними
Площадь параллелограмма равна
половине произведения егоS=
диагоналей
10. Свойство произвольного четырехугольника, связанное с параллелограммом.
Если соединитьотрезками середины
соседних сторон любого
четырёхугольника,
получится
параллелограмм.
11. РОМБ.
Определение: ромбом называется параллелограмм, укоторого все стороны равны.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба: диагонали ромба
перпендикулярны и делят его углы пополам.
Прямые, содержащие
диагонали, являются
осями симметрии.
взаимно
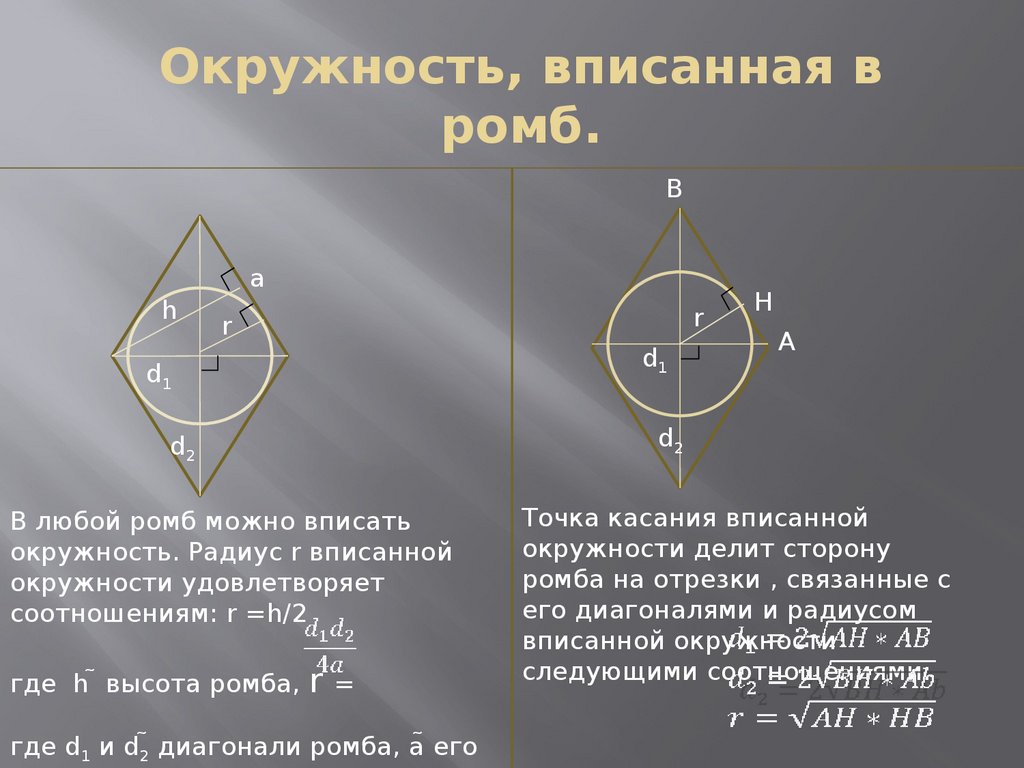
12. Окружность, вписанная в ромб.
Ba
h
r
r
d1
d1
A
d2
d2
В любой ромб можно вписать
окружность. Радиус r вписанной
окружности удовлетворяет
соотношениям: r =h/2
где h высота ромба,
H
r
=
где d1 и d2 диагонали ромба, a его
Точка касания вписанной
окружности делит сторону
ромба на отрезки , связанные с
его диагоналями и радиусом
вписанной окружности
следующими соотношениями:
13. Площадь ромба.
a ar
d1
d2
h
Через сторону и высоту:
S=ah
Через сторону и радиус
вписанной окружности:
S=2ar.
Через сторону и угол
ромба:
S=a2sin .
Через диагонали:
14. Прямоугольник.
Определение: прямоугольником называется параллелограмм, укоторого все углы прямые.
Прямоугольник обладает всеми свойствами параллелограмма.
Особое свойство
прямоугольника:
диагонали
прямоугольника
Две стороны
равны.
параллельны и углы,
Перпендикуля
прилежащие к одной
ры к
из этих сторон,
сторонам,
прямые.
проходящие
через их
середины,
являются
осями
Две противолежащие стороны равны и углы,
симметрии.
прилежащие к одной из этих сторон,
прямые.
15. Окружность, описанная около прямоугольника.
Rd
a
b
Около любого
прямоугольника
можно описать
окружность.
Радиус описанной
окружности R=d/2,
где
диагональ
прямоугольника.
16. Площадь прямоугольника.
db
Через диагональ и угол
между диагоналями:
d
a
Через стороны: S=a*b.
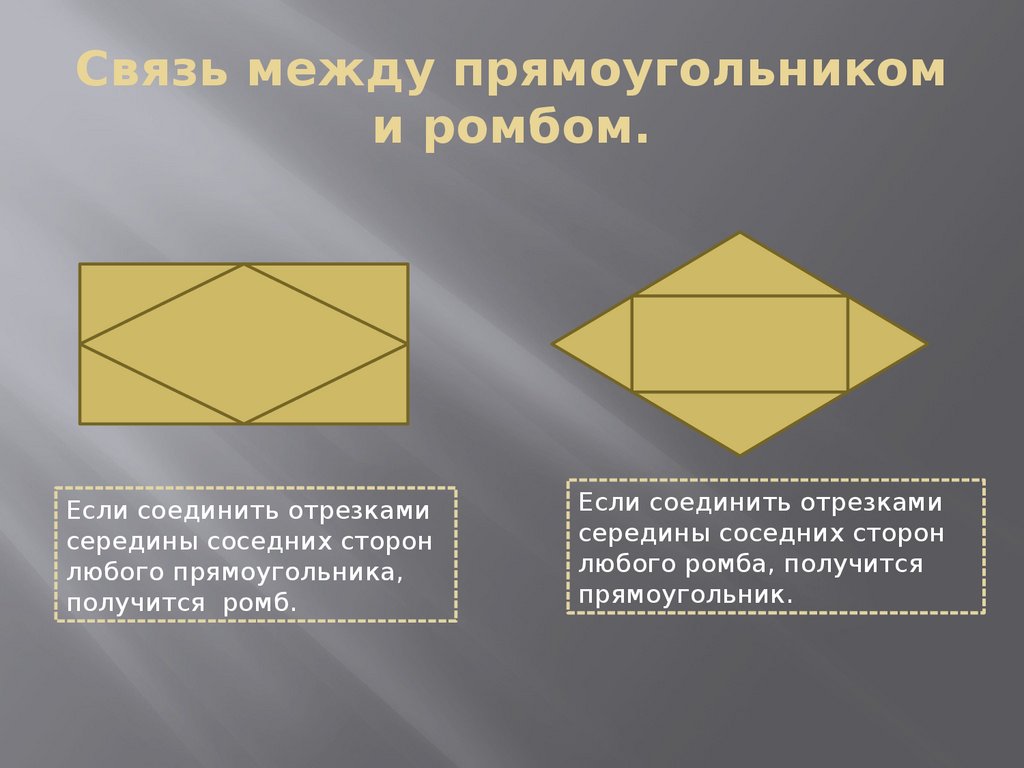
17. Связь между прямоугольником и ромбом.
Если соединить отрезкамисередины соседних сторон
любого прямоугольника,
получится ромб.
Если соединить отрезками
середины соседних сторон
любого ромба, получится
прямоугольник.
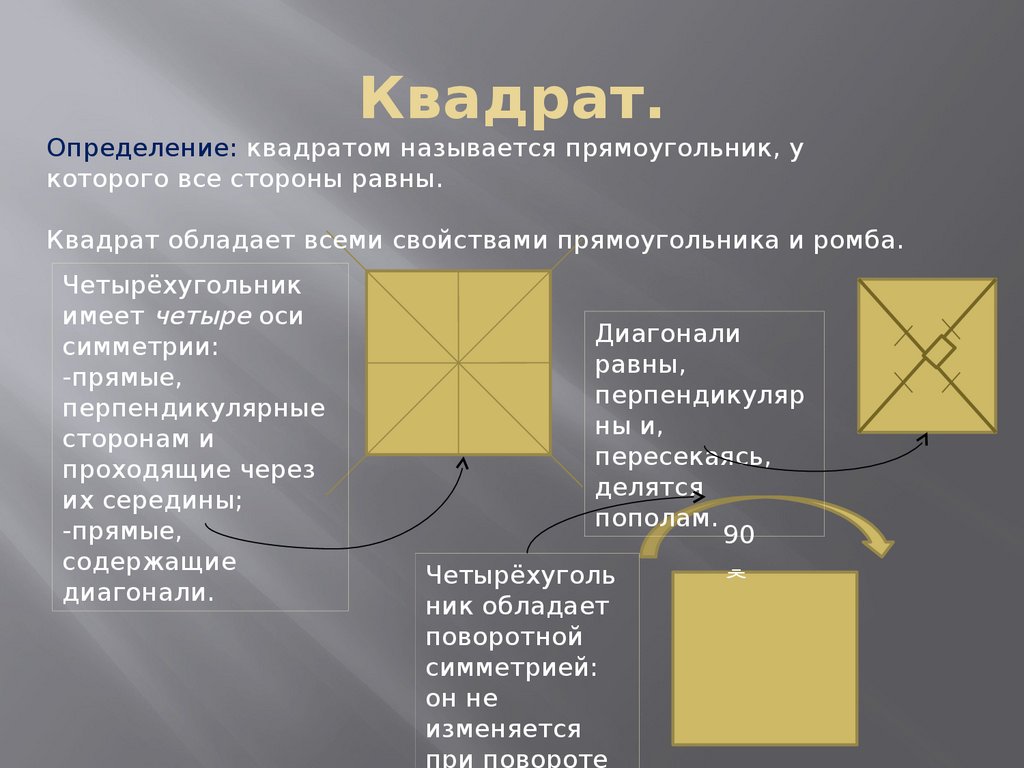
18. Квадрат.
Определение: квадратом называется прямоугольник, укоторого все стороны равны.
Квадрат обладает всеми свойствами прямоугольника и ромба.
Четырёхугольник
имеет четыре оси
симметрии:
-прямые,
перпендикулярные
сторонам и
проходящие через
их середины;
-прямые,
содержащие
диагонали.
Диагонали
равны,
перпендикуляр
ны и,
пересекаясь,
делятся
пополам.
90
Четырёхуголь
ник обладает
поворотной
симметрией:
он не
изменяется
19. Окружность, описанная около квадрата.
Около квадрата можноописать окружность.
R
a
Радиус описанной
окружности выражается
через сторону a квадрата
и его диагональ d
следующим образом:
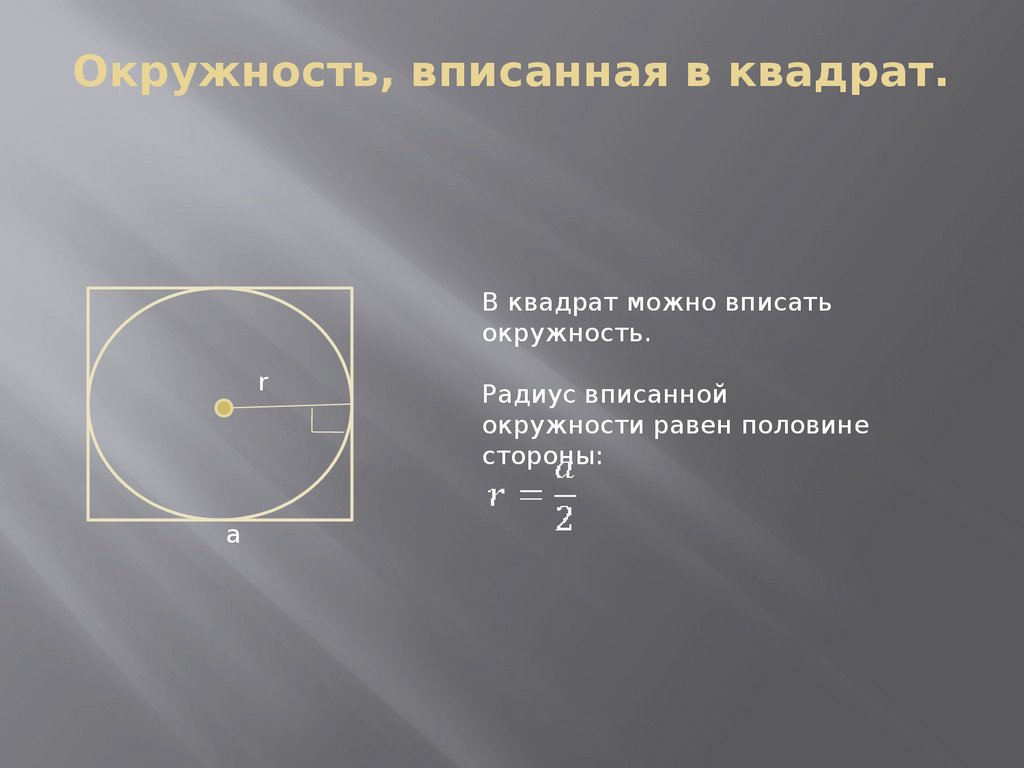
20. Окружность, вписанная в квадрат.
В квадрат можно вписатьокружность.
r
a
Радиус вписанной
окружности равен половине
стороны:
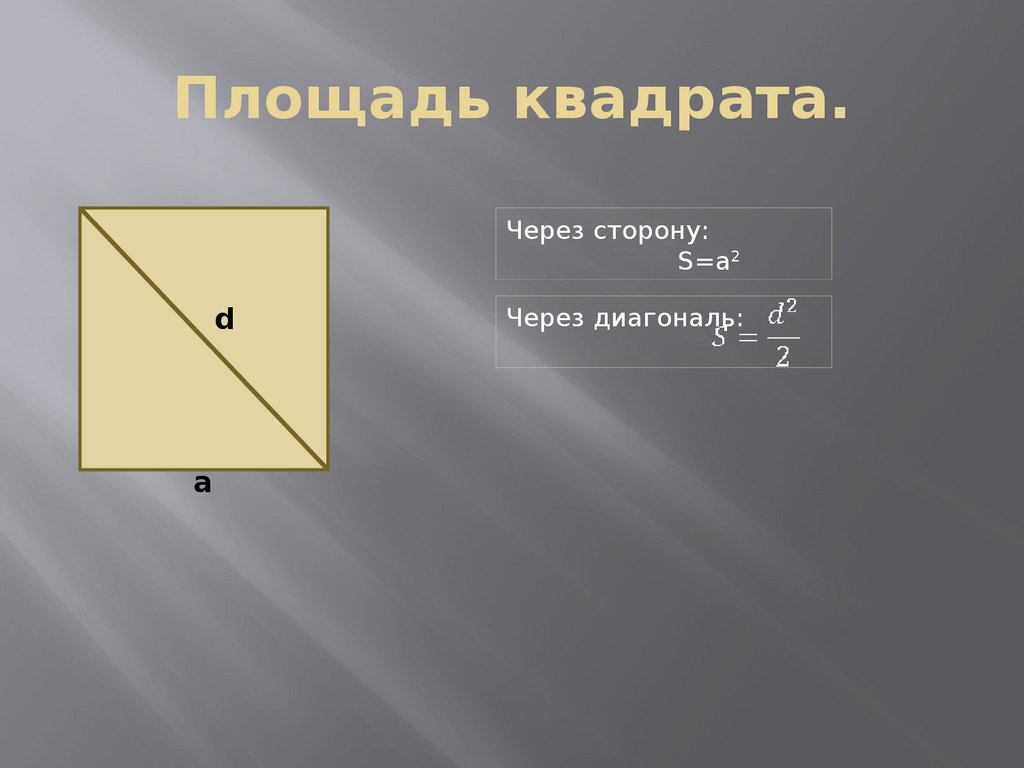
21. Площадь квадрата.
Через сторону:S=a2
d
a
Через диагональ:
22. Трапеция.
Определение:Трапецией
называется
четырехугольник, у которого две стороны
параллельны,
а
две
другие
стороны
не
параллельны. Параллельные стороны трапеции
называются ее основаниями, а две другие
стороны – боковыми сторонами.
Трапеция
называется
равнобедренной,
если
ее
боковые стороны равны.
Трапеция,
один
который прямой,
из
углов
называется
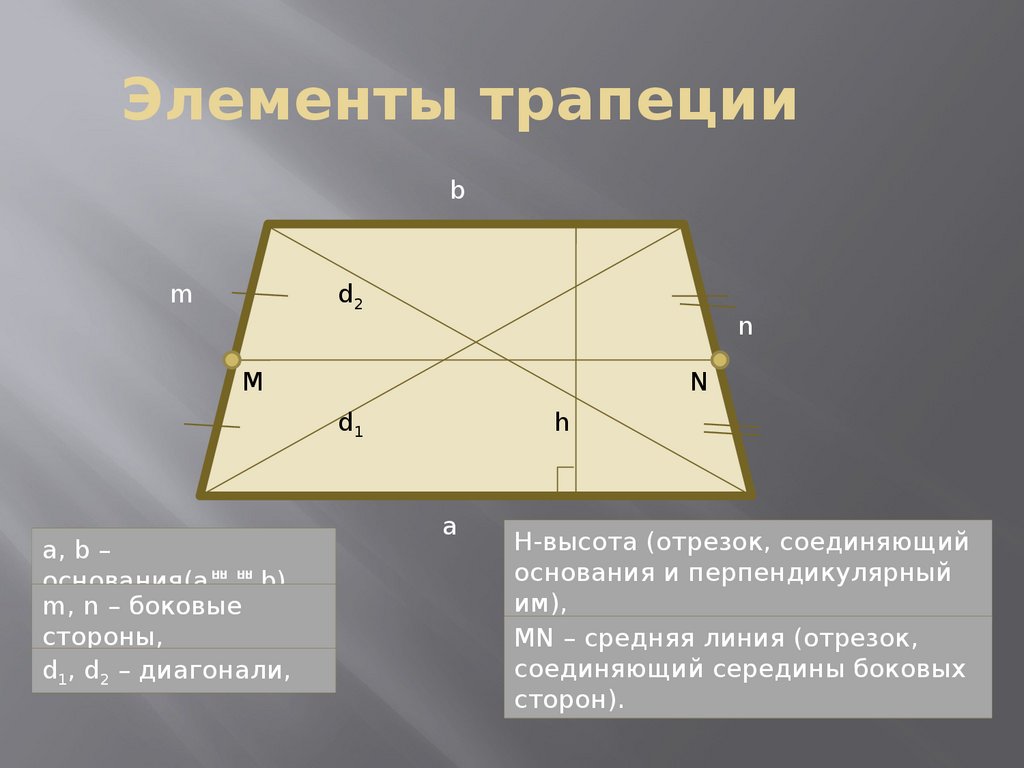
23. Элементы трапеции
bm
d2
n
M
N
d1
a, b –
основания(a b),
m, n – боковые
стороны,
d1, d2 – диагонали,
h
a
H-высота (отрезок, соединяющий
основания и перпендикулярный
им),
MN – средняя линия (отрезок,
соединяющий середины боковых
сторон).
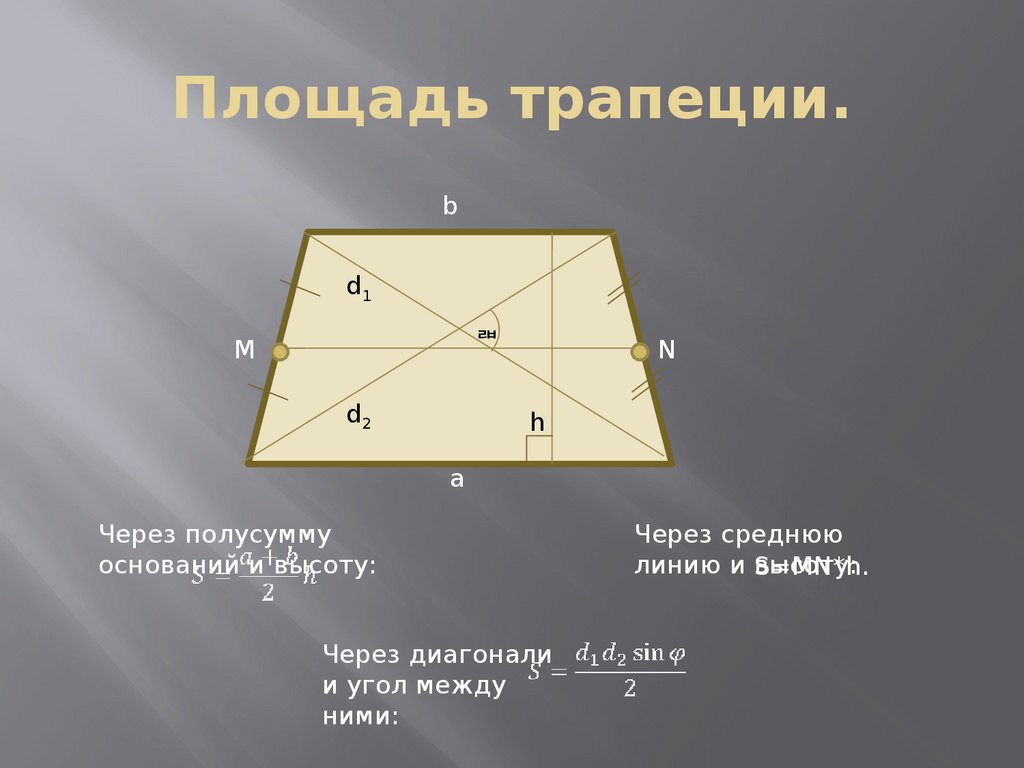
24. Площадь трапеции.
bd1
M
d2
N
h
a
Через полусумму
оснований и высоту:
Через диагонали
и угол между
ними:
Через среднюю
линию и S=MN*h.
высоту:
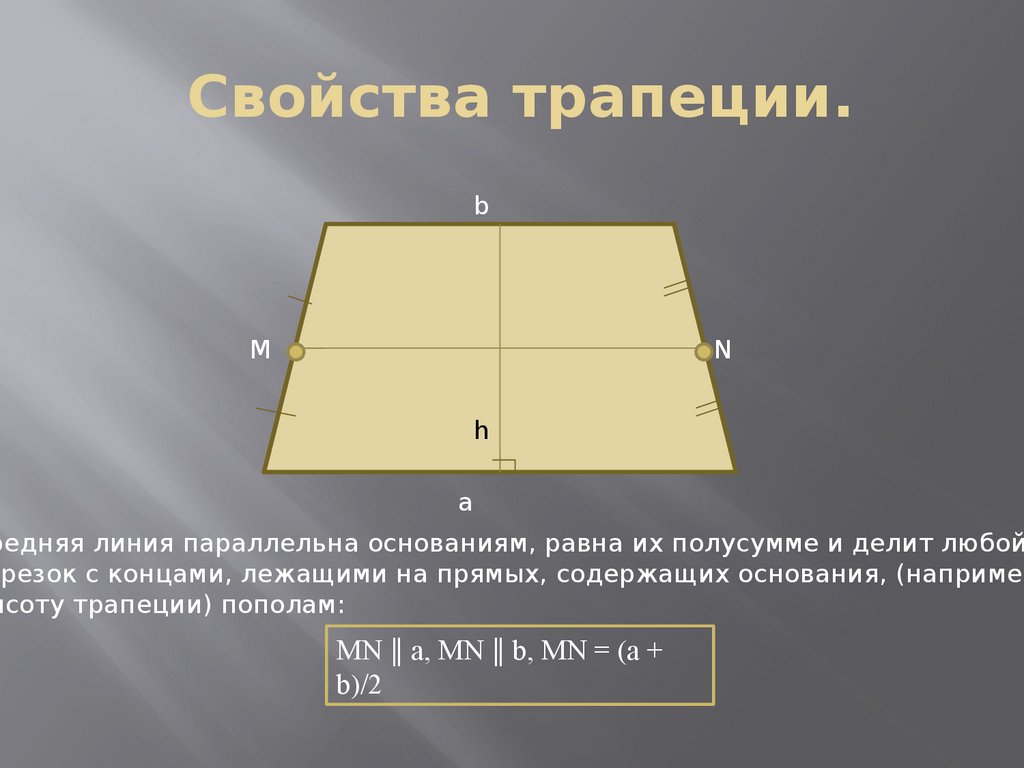
25. Свойства трапеции.
bM
N
h
a
редняя линия параллельна основаниям, равна их полусумме и делит любой
трезок с концами, лежащими на прямых, содержащих основания, (например
ысоту трапеции) пополам:
MN ‖ a, MN ‖ b, MN = (a +
b)/2
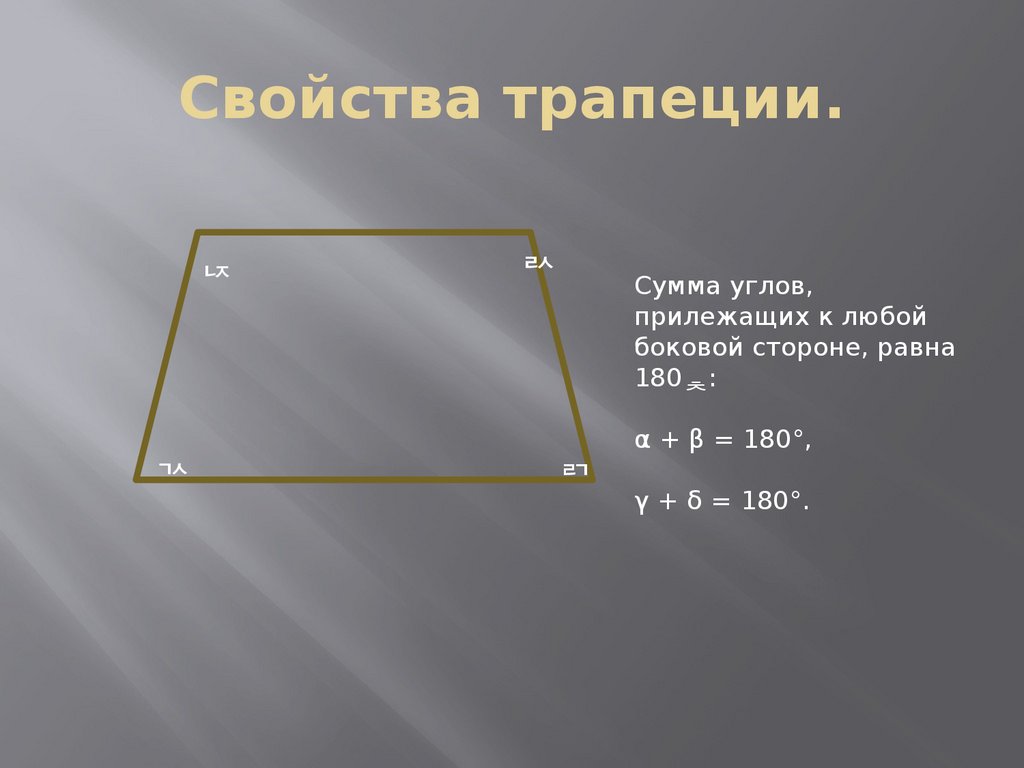
26. Свойства трапеции.
Сумма углов,прилежащих к любой
боковой стороне, равна
180 :
α + β = 180°,
γ + δ = 180°.
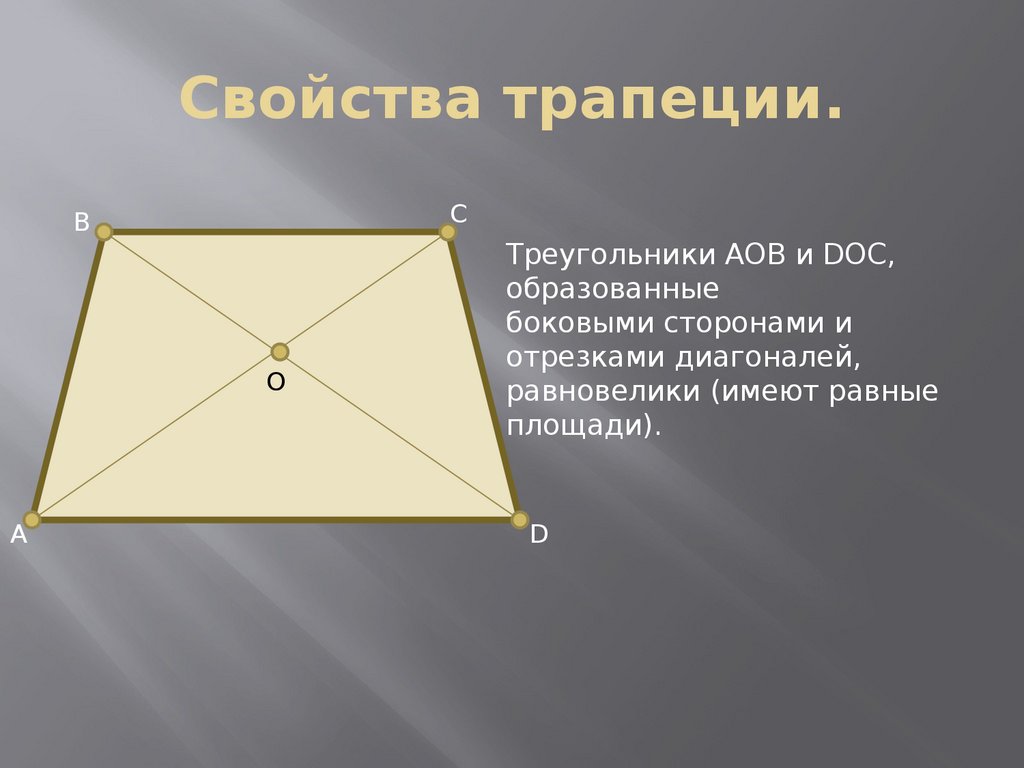
27. Свойства трапеции.
CB
O
A
Треугольники AOB и DOC,
образованные
боковыми сторонами и
отрезками диагоналей,
равновелики (имеют равные
площади).
D
28. Свойства трапеции.
BA
C
Треугольники AOD и СОВ,
образованные основаниями
и отрезками диагоналей,
подобны.
O
Коэффициент подобия κ
равен отношению
оснований:
κ = AD/BC
D Отношение
площадей этих
∆ AOD и ∆ COB подобны.
треугольников
равно κ².
29.
AB
C
Любой
отрезок,
соединяющий
основания и проходящий через точку
пересечения диагоналей трапеции,
делится этой точкой в отношении
O
OX/OY = BC/AD
A
Y
Это справедливо, в том числе, для
D самих диагоналей и высот.
30.
Любуюравнобедренную
трапецию
можно
вписать
в
окружность.
Вписать в
только
трапецию.
окружность можно
равнобедренную
31.
ВС
r
r
O
r
А
r
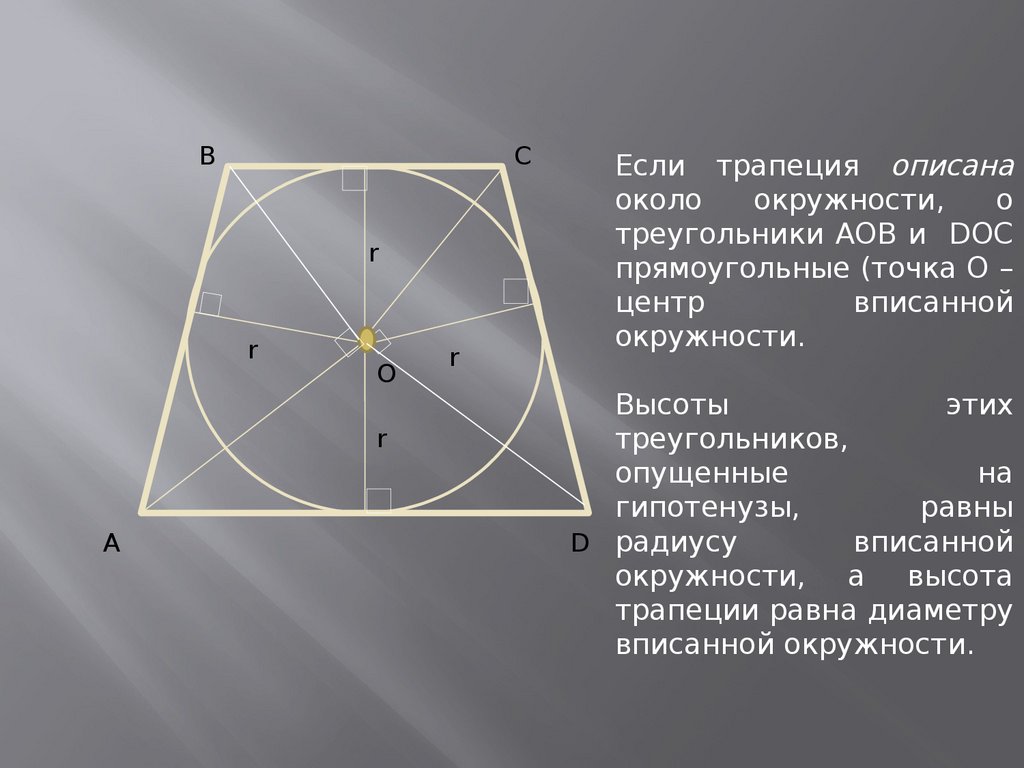
Если трапеция описана
около
окружности,
о
треугольники АОВ и DOC
прямоугольные (точка О –
центр
вписанной
окружности.
Высоты
этих
треугольников,
опущенные
на
гипотенузы,
равны
вписанной
D радиусу
окружности, а высота
трапеции равна диаметру
вписанной окружности.



















 Математика
Математика Информатика
Информатика








