Подготовка к ЕГЭ С5

1. Подготовка к ЕГЭ

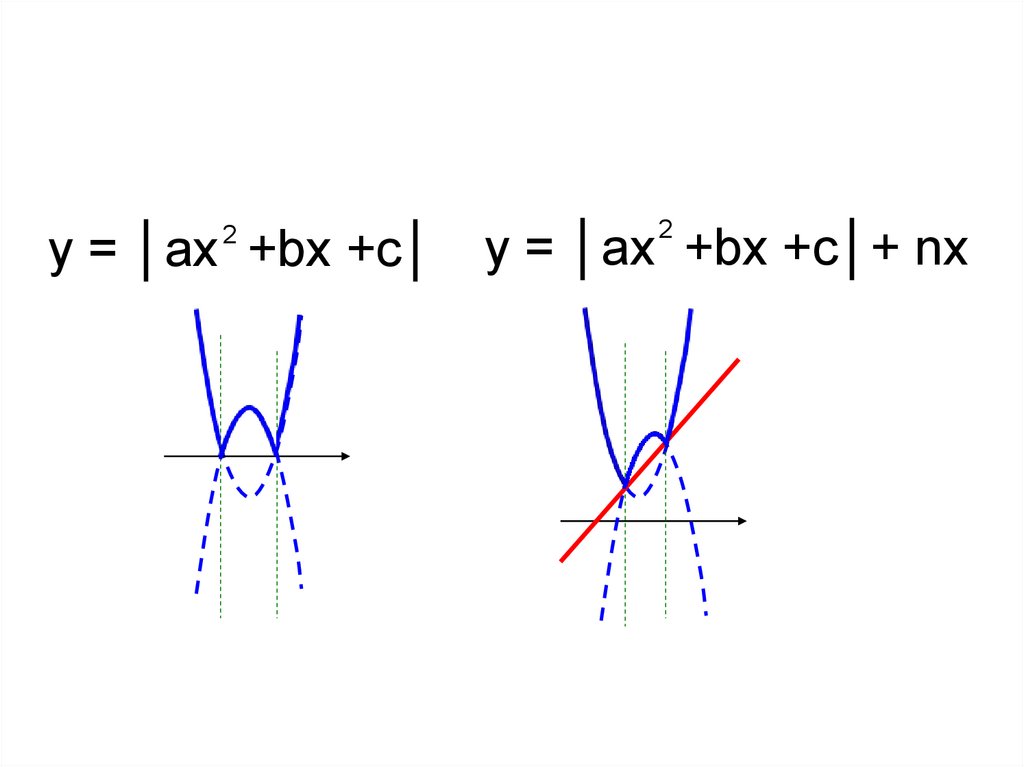
С5

2. y = │ax +bx +c│

y = │ax +bx +c│+ nx
2
2

3. Найдите все значения а, при каждом из которых наименьшее значение функции y = 4ax + |x - 6x +5| больше, чем -24

Найдите все значения а, при каждом из которых
наименьшее значение функции
y = 4ax + |x2 - 6x +5| больше, чем -24
1. рассмотрим функцию на двух отрезках:
2
2
x - 6x +5≥0 и x - 6x +5<0
2. Наименьшее значение функция будет
принимать в вершине параболы или на
концах отрезка.

4. x - 6x + 5 ≥ 0

1 случай
x - 6x + 5 ≥ 0
2
х≤1
х≥5
2
y = 4ax + x - 6x + 5
2
y = x + 2(2a – 3) + 5 – ветви направлены
вверх
ось симметрии параболы – прямая х = хв
хв = (-2(2а – 3))/2
хв = 3 - 2а

5. Ветви направлены вверх

х≤1
х≥5
Ветви направлены вверх
Возможны 4 случая
расположения параболы:

6. x - 6x + 5 < 0

2 случай
2
x - 6x + 5 < 0
1<х<5
y = 4ax - x 2 + 6x - 5
y = -x2 + 2(2a + 3) - 5 – ветви направлены
вниз
ось симметрии параболы – прямая х = хв
хв = (-2(2а + 3))/2
хв = - 3 - 2а

7. Ветви направлены вниз

1≤х≤5
Ветви направлены вниз
Добавим к первому случаю
четыре возможных
расположения параболы:

8. При возможны три случая

х≤1
При х≥5
возможны три случая
наименьшего значения функции
• f (1)
• f (5)
• f (xв) = f (3 - 2a)
Составим систему:
f (1) > -24
f (5) > -24
f (3 - 2a) > -24
3х – 2a ≤1
3
х – 2a ≥5
a>-6
a > -1,2
(3-√29)/2<a<(3+√29)/2
a≤-1
a≥1
(3-√29)/2< a ≤ -1
1 ≤a< (3+√29)/2

9. При возможны два случая

При 1<x<5 возможны два случая
наименьшего значения функции
• f (1)
• f (5)
Составим систему:
f (1) > -24
f (5) > -24
3
х – 2a >1
3
х – 2a <5
a>-6
a > -1,2
a>-1
a<1
-1 < a < 1

10.

(3-√29)/2< a ≤ -1
1 ≤a< (3+√29)/2
-1 < a < 1
Ответ: (3-√29)/2< a < (3+√29)/2

11.

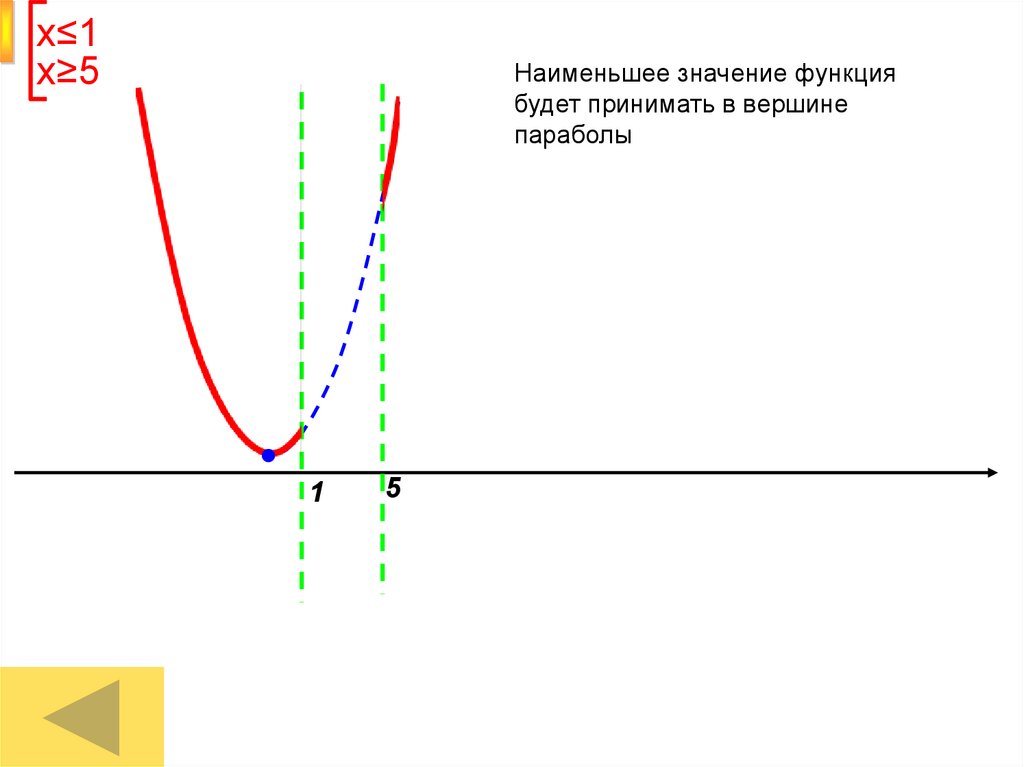
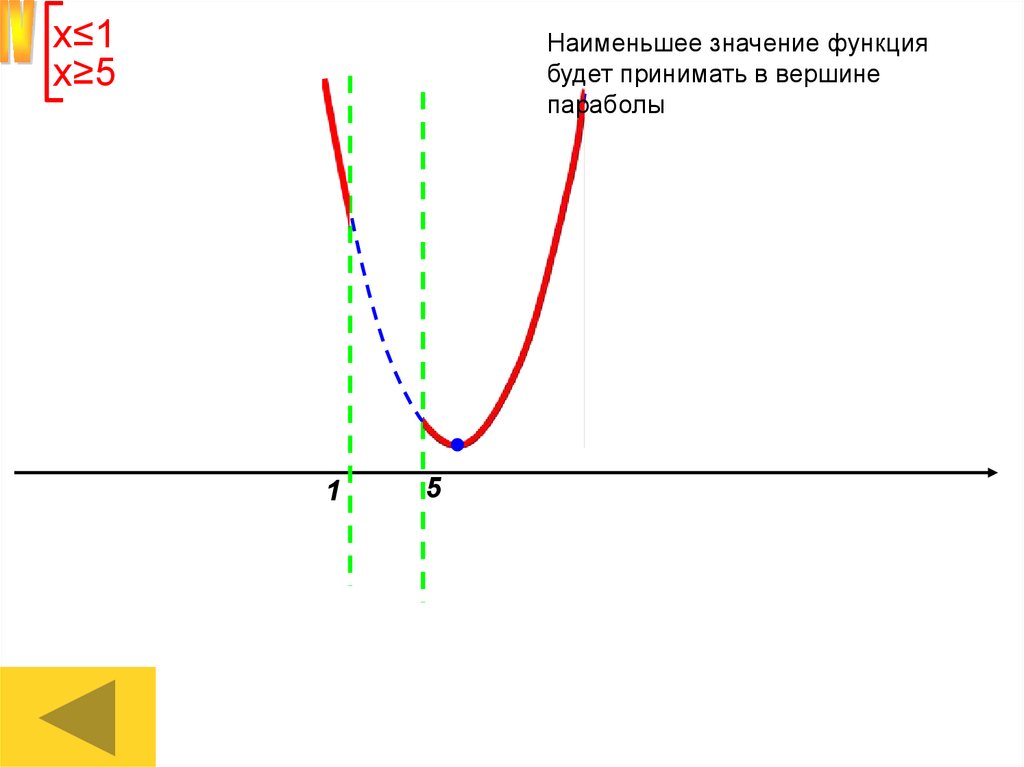
х≤1
х≥5
Наименьшее значение функция
будет принимать в вершине
параболы
1
5

12.

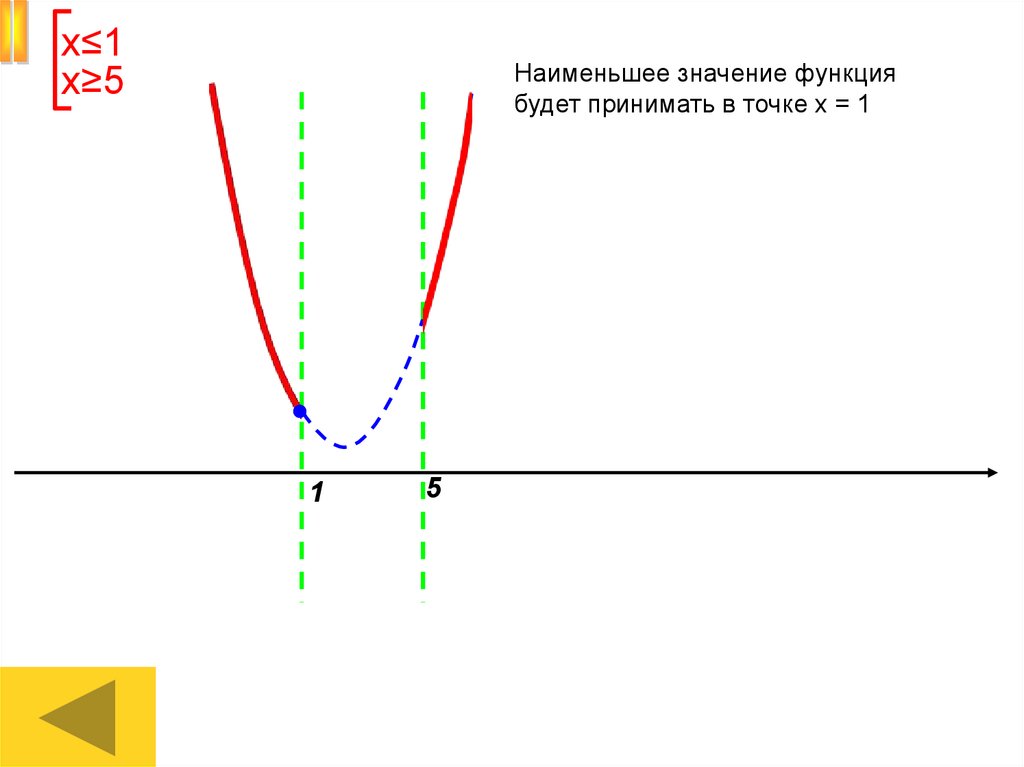
х≤1
х≥5
Наименьшее значение функция
будет принимать в точке х = 1
1
5

13.

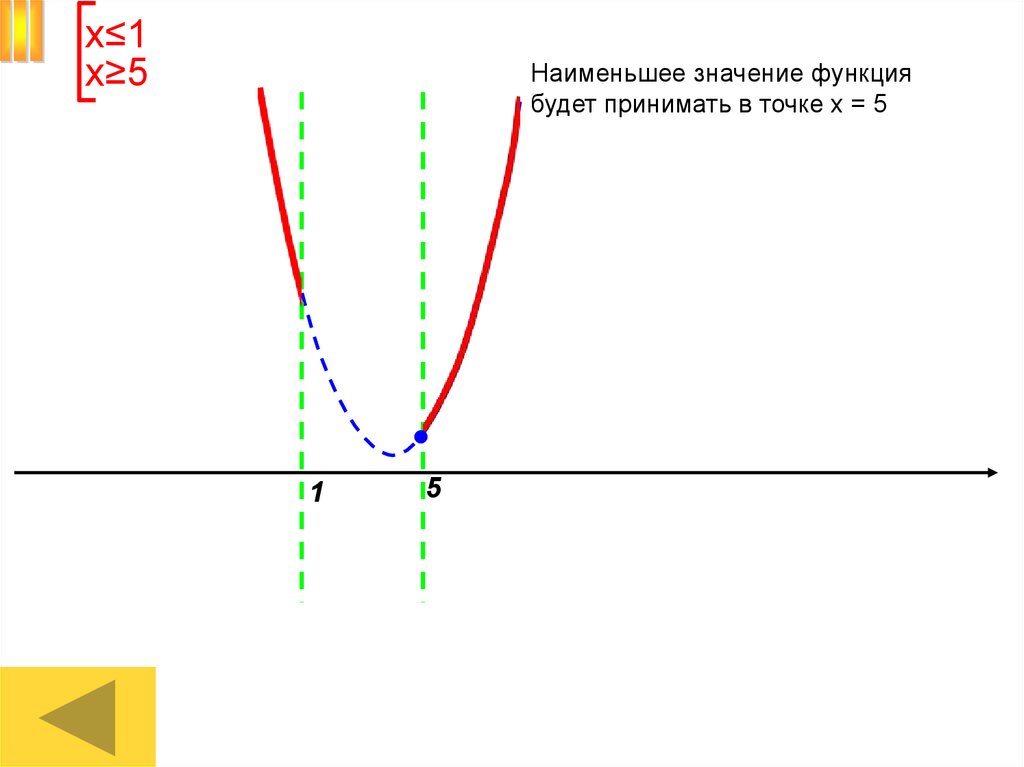
х≤1
х≥5
Наименьшее значение функция
будет принимать в точке х = 5
1
5

14.

х≤1
х≥5
Наименьшее значение функция
будет принимать в вершине
параболы
1
5

15.

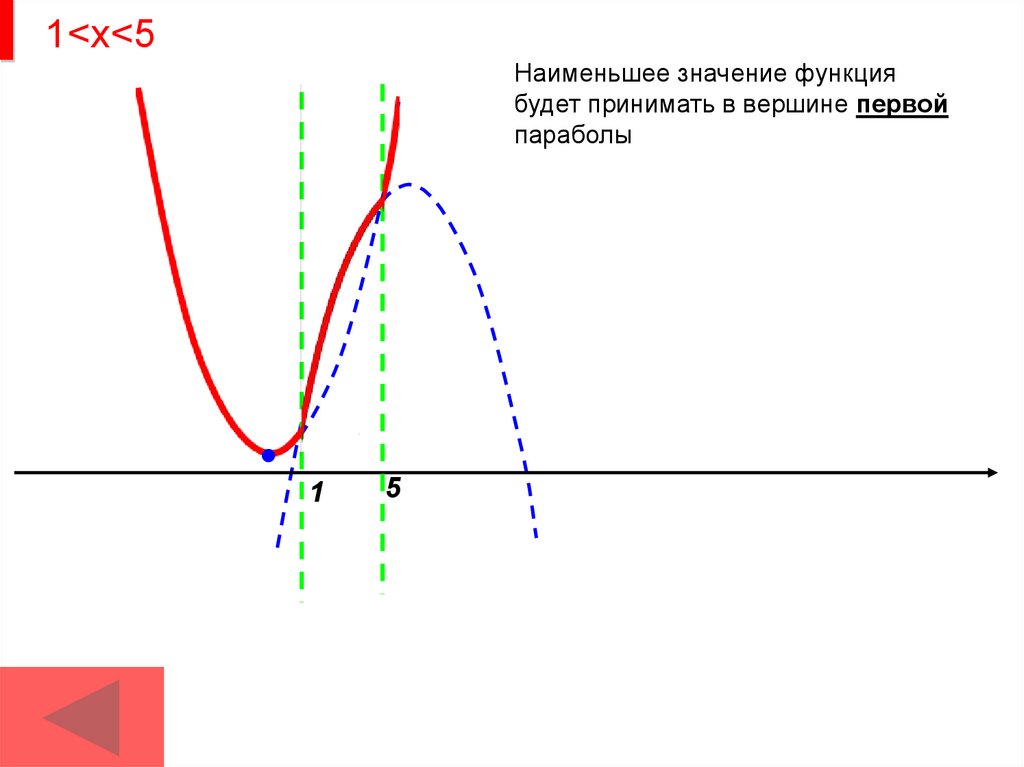
1<х<5
Наименьшее значение функция
будет принимать в вершине первой
параболы
1
5

16.

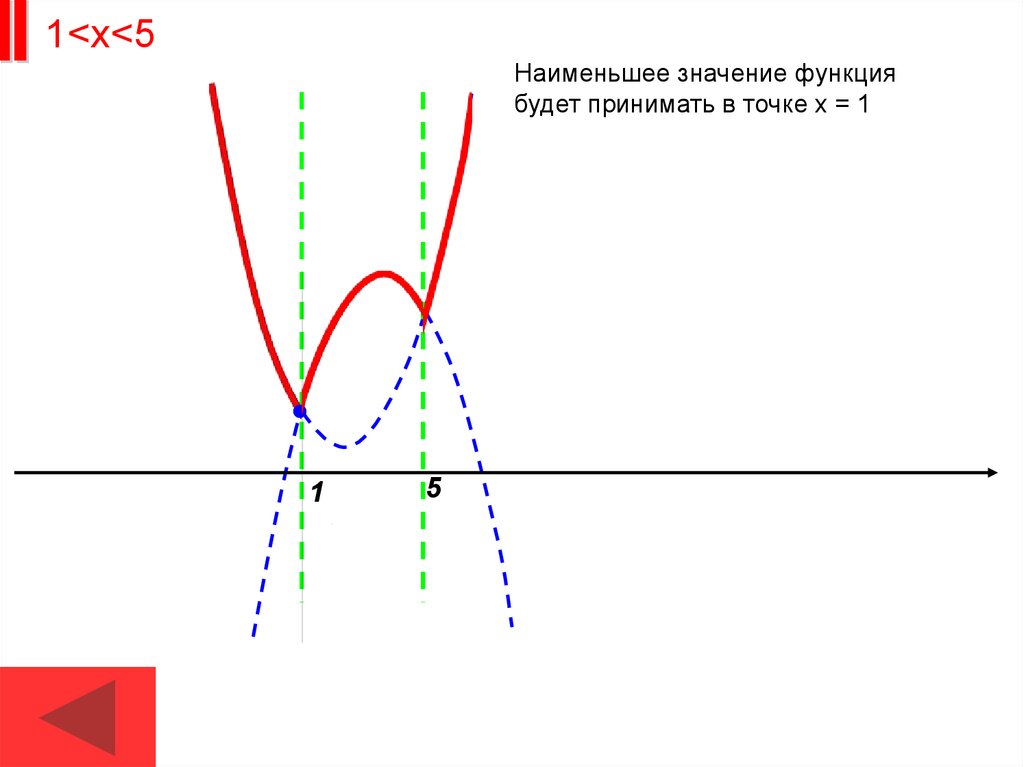
1<х<5
Наименьшее значение функция
будет принимать в точке х = 1
1
5

17.

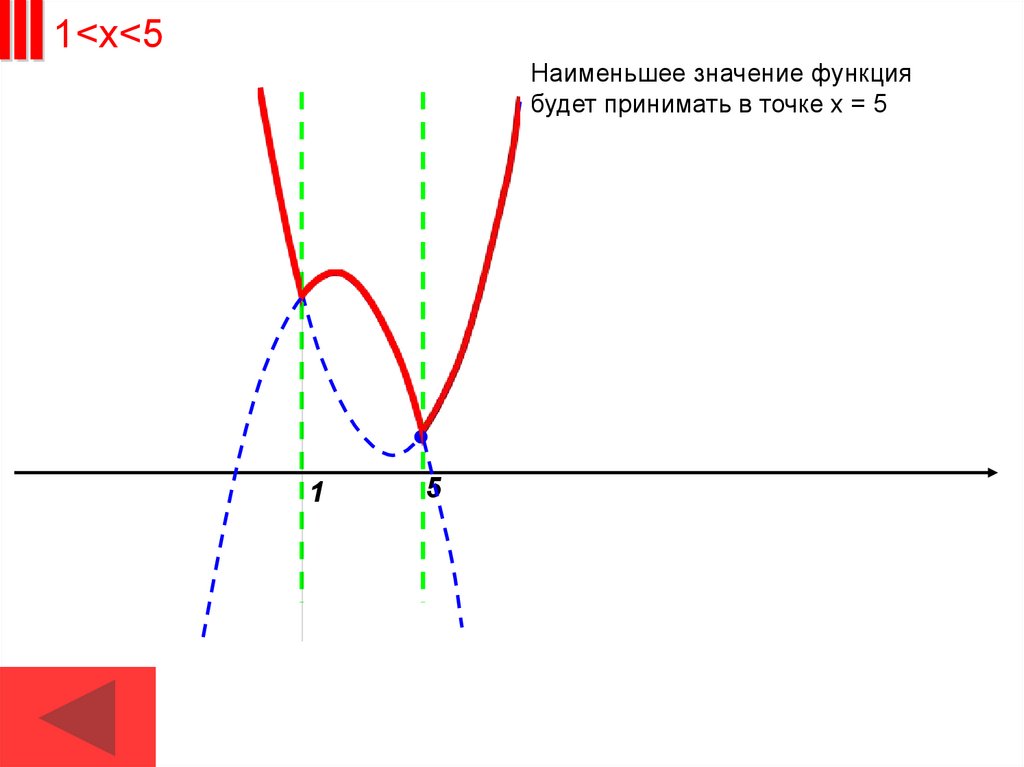
1<х<5
Наименьшее значение функция
будет принимать в точке х = 5
1
5

18.

1<х<5
Наименьшее значение функция
будет принимать в вершине первой
параболы
1
5