Похожие презентации:
Подготовка к ЕГЭ
1. МОУ СОШ с. Донское Задонского района Липецкой области
Разработалаучитель математики
Васильева Т. А.
2. На рисунке изображена прямая, являющаяся касательной к графику функции y=f(x) в точке (хо; f(xо). Найдите значение производной
y=f ´(x) в точке хо.3. На рисунке дан график функции y=f(x) и построена касательная к некоторой точке х графика этой функции .Найти значение
f'(x)=k=2На рисунке дан
график функции
y=f(x) и построена
касательная к
некоторой точке х
графика этой
функции .Найти
значение
производной в
этой точке.
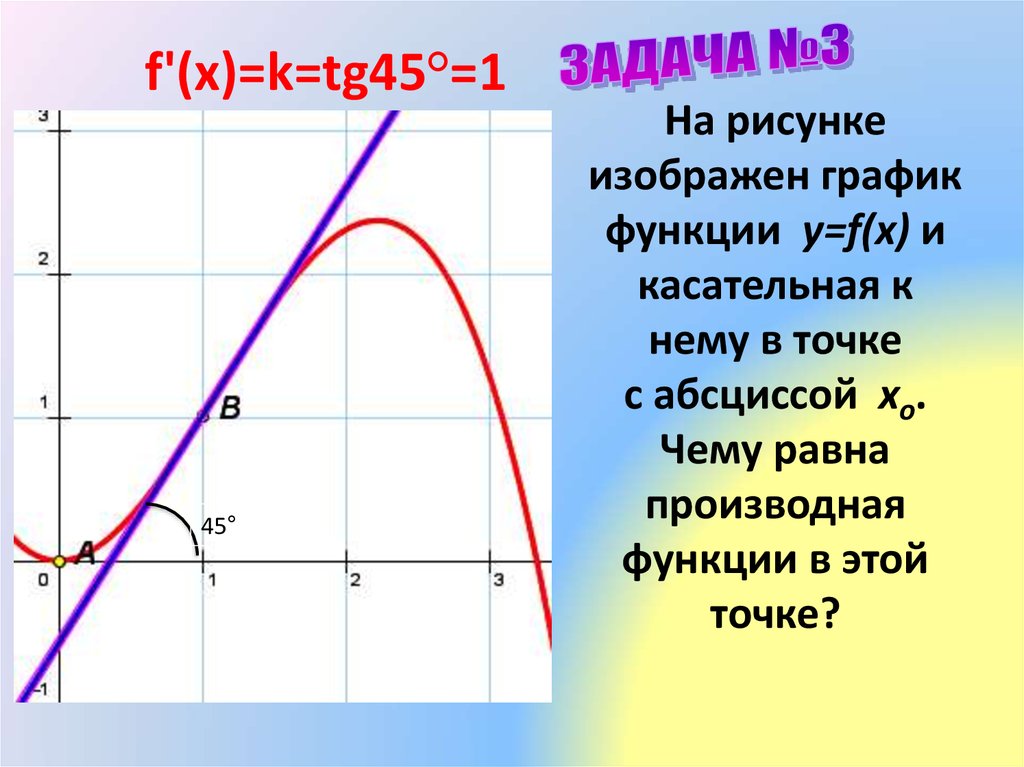
4. На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой хо. Чему равна производная функции в этой
f'(x)=k=tg45°=145°
На рисунке
изображен график
функции y=f(x) и
касательная к
нему в точке
с абсциссой хо.
Чему равна
производная
функции в этой
точке?
5.
количество положительных коэффициентов равно 2На рисунке изображены
прямые, являющиеся
касательными к
графику функции y=f(x)
в точках с абсциссами
х1, х2, х3, х4, х5.
Определите количество
положительных чисел
среди значений
производной в точках
х1, х2, х3, х4, х5.
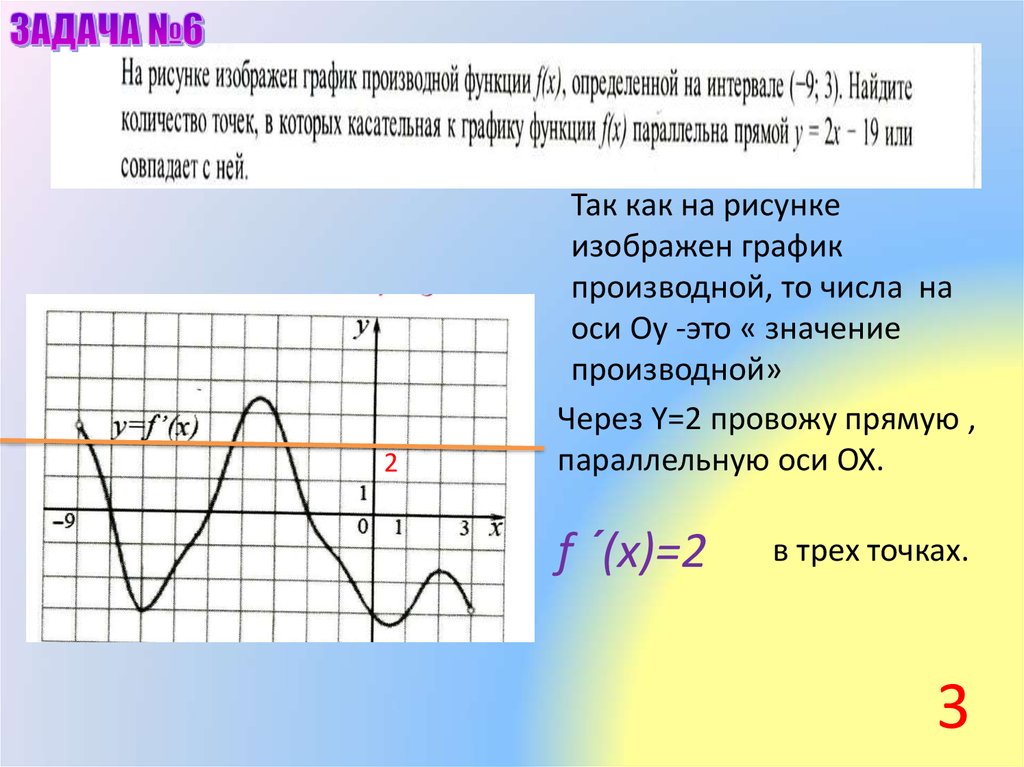
6.
Касательная к графику функцииy=f(x), проведенная в точке а
параллельна прямой y= 3x - 5.
Определить угловой коэффициент
касательной;
Найти значение производной в
точке а.
7. =
2Так как на рисунке
изображен график
производной, то числа на
оси Оy -это « значение
производной»
Через Y=2 провожу прямую ,
параллельную оси OX.
f ´(x)=2
в трех точках.
3
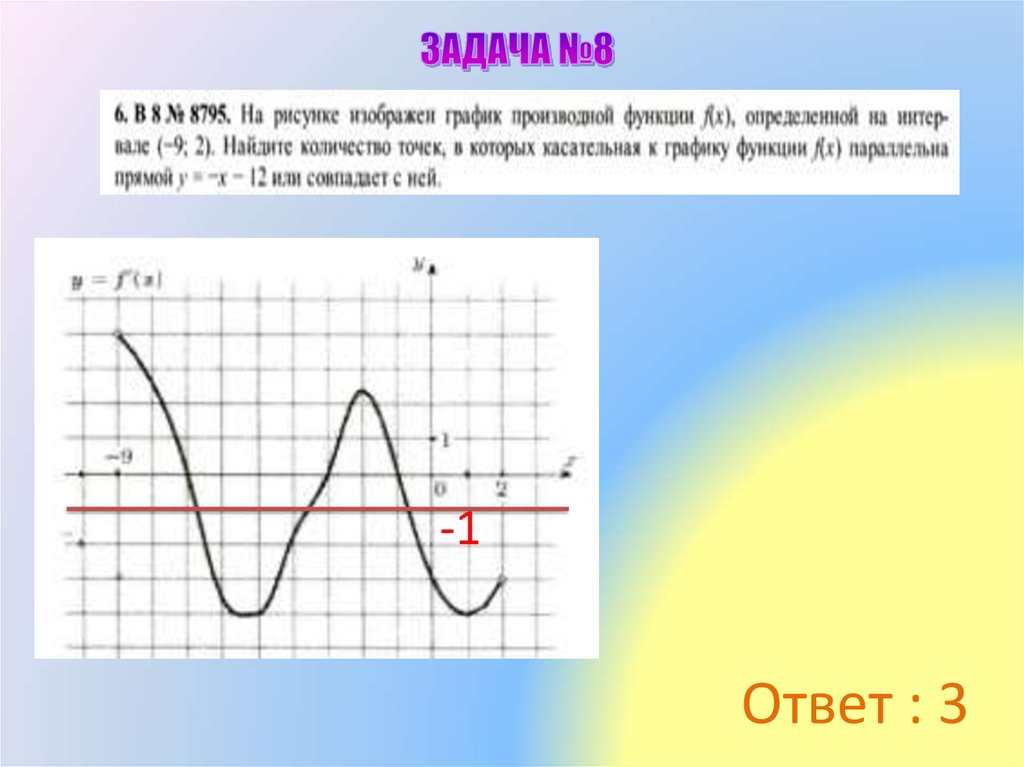
8.
6Ответ: 5
5
9.
Ответ : 310.
На рисунке изображён графикy = f ′(x) — производной
функции f(х),
определенной на интервале
(−19; 2).
Найдите число точек
минимума
функции f (x),
принадлежащих отрезку
[−17; − 1] .
11.
Материальная точка М начинаетдвижение из точки А и движется
по
прямой в течение 10 секунд.
График показывает, как
менялось
расстояние от точки А до точки
М с течением времени. На оси
абсцисс
откладывается время в секундах,
на оси ординат – расстояние в
метрах.
Определите, сколько раз за
время движения скорость точки
М
обращалась в ноль (начало и
конец движения не учитывайте).
12.
На рисунке изображёнграфик – производной
y = f ′(x) функции
f(x),опредёленной на
интервале(-2;5) . По
рисунку найдите точку
минимума функции .
13.
На рисунке изображёнграфик функции y = f
(x),
определённой на
интервале (1; 11) . По
рисунку найдите
корень уравнения
f′(x) = 0,
принадлежащий
интервалу(2; 6)
14.
На рисунке изображёнграфик y = f ′(x) —
производной функции
f (x),определённой на
интервале (−10; 14).
Найдите число точек
максимума функции f (x) ,
принадлежащих
отрезку [−8; 11] .











 Математика
Математика








