Диалоги о параболе. 9 класс

1. Диалоги о параболе

МБОУ Игримская СОШ №2, Салий Татьяна Анатольевна,
учитель математики

2.

3. Цели и задачи урока:

1. Повторить свойства квадратичной
функции.
2. Показать связь квадратичной
функции и её графика с реальным
миром.
3. Систематизировать знания по
применению свойств параболы.

4. Определение.

у
у
0
х
Определение.
0
Функция вида у = ах2+bх+с,
где а, b, c – заданные числа, а≠0,
х – действительная переменная,
называется квадратичной функцией.
Примеры:
1) у=5х+1
2) у=3х2-1
3) у=-2х2+х+3
4) у=x3+7x-1
5) у=4х2
6) у=-3х2+2х
х

5.

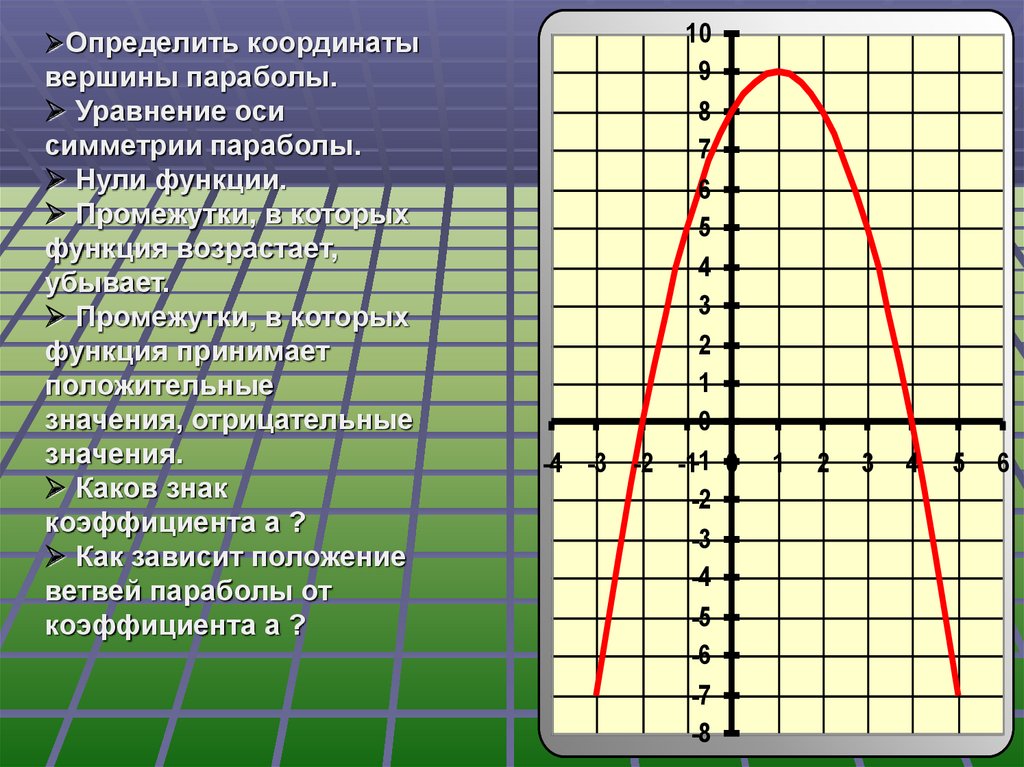
Определить координаты
вершины параболы.
Уравнение оси
симметрии параболы.
Нули функции.
Промежутки, в которых
функция возрастает,
убывает.
Промежутки, в которых
функция принимает
положительные
значения, отрицательные
значения.
Каков знак
коэффициента a ?
Как зависит положение
ветвей параболы от
коэффициента a ?
10
9
8
7
6
5
4
3
2
1
0
-4 -3 -2 -1-1 0
-2
-3
-4
-5
-6
-7
-8
1
2
3
4
5
6

6. Вершина параболы:

b
х0
; y 0 y ( x0 )
2a
Уравнение оси симметрии: х=х0
Задание.
Найти координаты вершины параболы:
1) у = х 2 -4х-5
2) у=-5х 2+3
Ответ:(2;-9)
Ответ:(0;3)

7. Координаты точек пересечения параболы с осями координат.

С Ох: у=0
С Оу: х=0
ах2+bх+с=0
у=с
Задание.
Найти координаты точек пересечения
параболы с осями координат:
1)у=х2-х;
(0;0);(1;0)
2)у=х2+3;
(0;3)
3)у=5х2-3х-2
(1;0);(-0,4;0);(0;2)

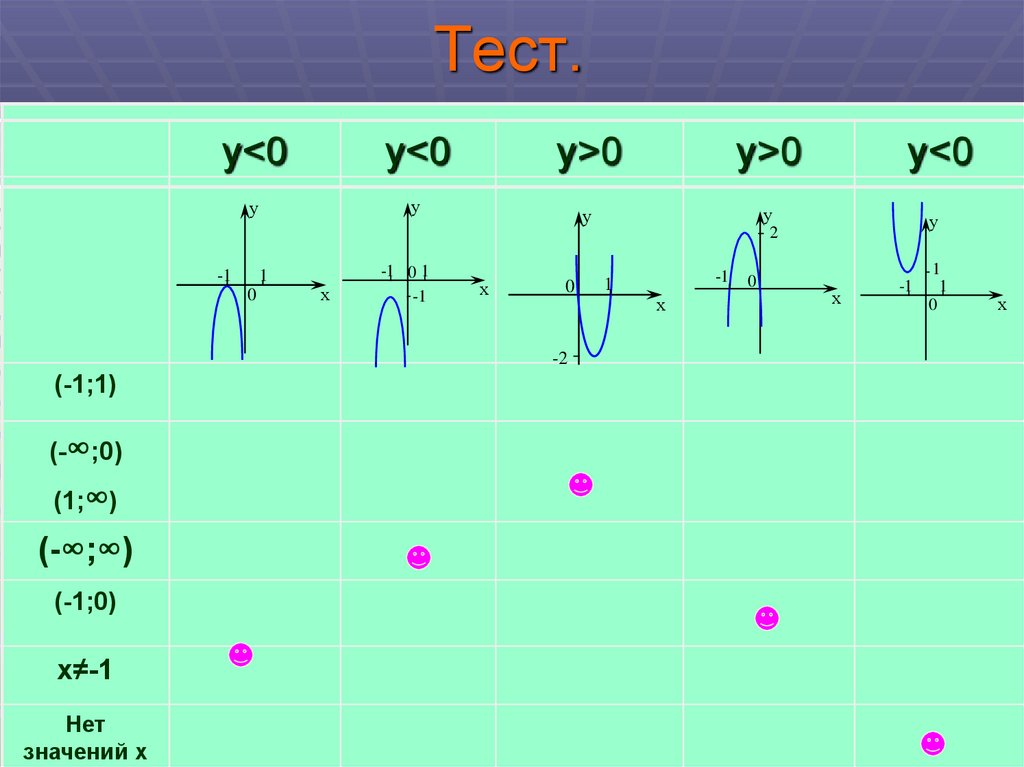
8. Тест.

у<0
у<0
у>0
у>0
у
у
у
у
2
-1
1
0
х
-1 0 1
-1
х
0
-2
(-1;1)
(-∞;0)
(1;∞)
(-∞;∞)
(-1;0)
х≠-1
Нет
значений х
-1
1
х
0
у<0
у
х
-1
1
1
0
х

9. Построить график функции и по графику выяснить ее свойства.

У=
2
-х -6х-8
Свойства функции:
у>0 на промежутке
у<0 на промежутке
Функция возрастает на
промежутке
Функция убывает на
промежутке
Наибольшее значение функции
равно
(-4;-2)
(-∞;-4);(2;∞)
(-∞;-3]
[-3;∞)
1, при х=-3

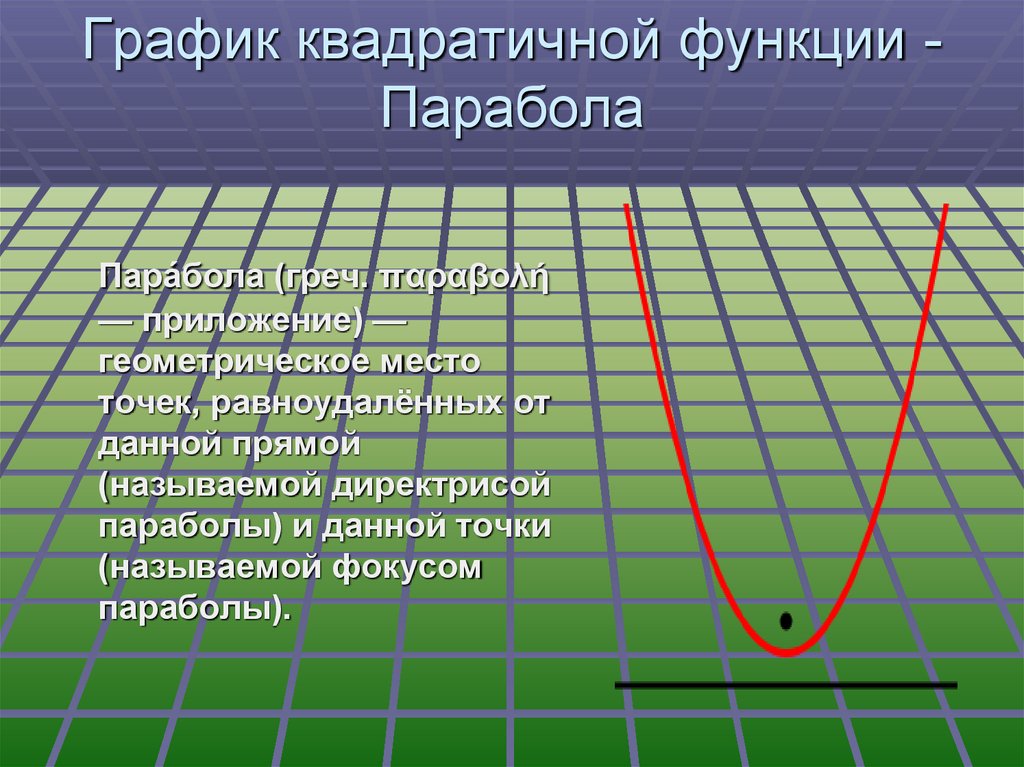
10. График квадратичной функции -Парабола

График квадратичной функции Парабола
Пара́бола (греч. παραβολή
— приложение) —
геометрическое место
точек, равноудалённых от
данной прямой
(называемой директрисой
параболы) и данной точки
(называемой фокусом
параболы).

11. Свойства

Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось
проходит через фокус и перпендикулярна директрисе.
Если фокус параболы отразить относительно касательной, то
его образ будет лежать на директрисе.
Парабола является антиподерой
у>0 прямой.
Все параболы подобны. Расстояние между фокусом и
директрисой определяет масштаб.
При вращении параболы вокруг оси симметрии получается
эллиптический параболоид.

12. Фокус Архимеда

Этот день 212 года до н.э. уцелевшим
римлянам запомнился на всю жизнь. Почти
полтысячи маленьких солнц вдруг загорелись
на крепостной стене. Сначала они просто
ослепили, но через некоторое время
произошло нечто фантастическое:
передовые римские корабли, подошедшие к
Сиракузам, один за другим вдруг начали
вспыхивать, как факелы. Бегство римлян
было паническим...

13. Согласно легенде, Архимед из Сиракуз сжёг флот римлян, обороняя свой город с помощью параболических зеркал. Свойства таких

зеркал применяют при конструировании
солнечных печей, телескопов и др.

14. Чудесная парабола

Люблю я петь и веселиться,
В весёлом танце покружиться.
Когда вокруг оси вращаюсь,
Фигурой важной обращаюсь.
А кавалеры подбегают,
К автомобилю провожают.
И каждый хочет пригласить –
На крыше дома погостить.
Загадка

15.

16. Тело, брошенное вверх, движется по параболе.

Пусть мяч подбросили
вертикально вверх с высоты
1,5 м, придав ему начальную
скорость 10м/с². Тогда
высота h (в м), на которой
находится мяч, есть
квадратичная функция
времени полета t (в с). Если
считать, что g =10 м/с, то
функцию h= f(t) можно
описать формулой
h= 1,5+10t-5t².
График этой функции - часть
параболы.

17. Применение свойств параболы при решении задач повышенной сложности.

1. Сколько корней имеет уравнение:
(х-100)(х-101)+(х- 101)(х-102)+(х-102)(х-100)=0?